4.3 探索三角形全等的条件 第1课时 课件(共18张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 4.3 探索三角形全等的条件 第1课时 课件(共18张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
第四章 三角形
4.3 探索三角形全等的条件
第1课时
1.知道要判定两个三角形全等至少需要三个条件.
2.探究第一种判定三角形全等的方式——边边边.(重点)
3.知道三角形具有稳定性.
一、学习目标
二、新课导入
复习回顾:
1.全等三角形的定义:
2.全等三角形的性质:
能够完全重合的两个三角形叫做全等三角形.
全等三角形对应边相等,对应角相等.
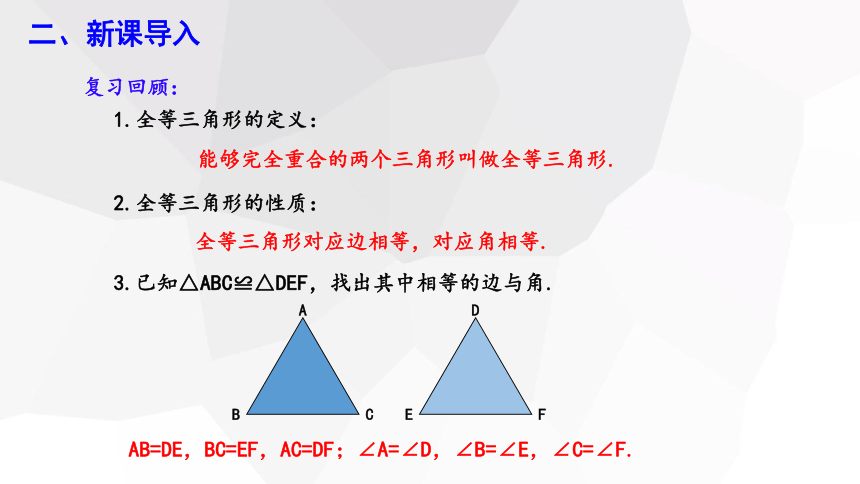
3.已知△ABC≌△DEF,找出其中相等的边与角.
A
B
C
D
E
F
AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠C=∠F.
三、概念剖析
既然我们知道全等三角形三组对应边相等,三组对应角相等.
A
B
C
D
E
F
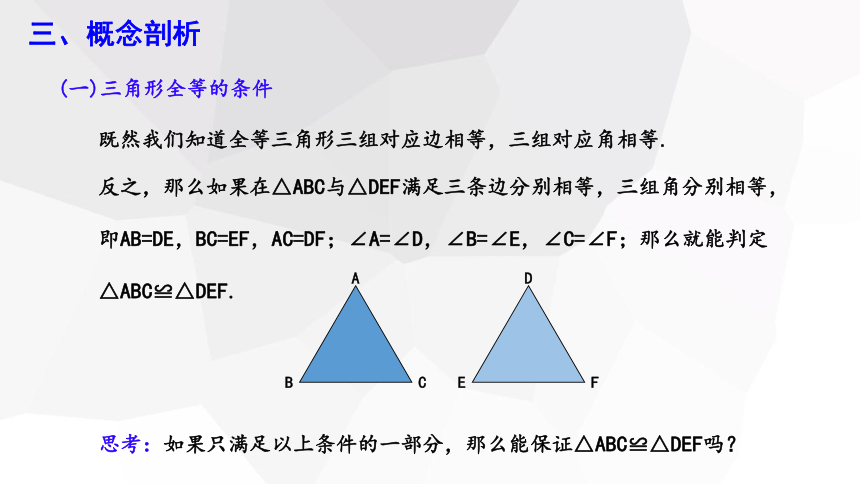
反之,那么如果在△ABC与△DEF满足三条边分别相等,三组角分别相等,
即AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠C=∠F;那么就能判定
△ABC≌△DEF.
(一)三角形全等的条件
思考:如果只满足以上条件的一部分,那么能保证△ABC≌△DEF吗?
三、概念剖析
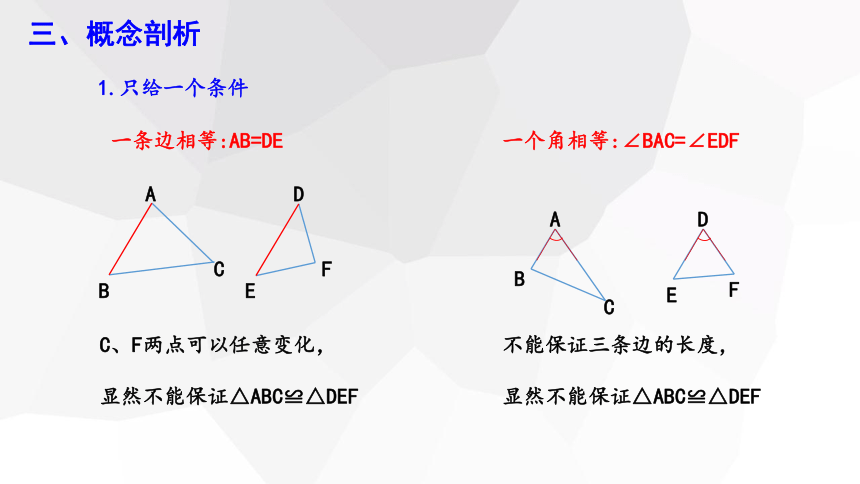
1.只给一个条件
一条边相等:AB=DE
一个角相等:∠BAC=∠EDF
A
B
C
D
E
F
C、F两点可以任意变化,
显然不能保证△ABC≌△DEF
A
B
C
D
E
F
不能保证三条边的长度,
显然不能保证△ABC≌△DEF
三、概念剖析
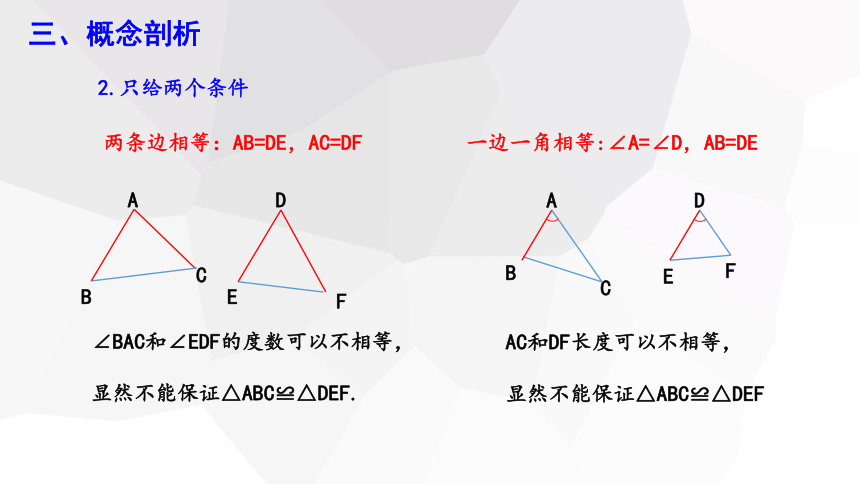
2.只给两个条件
两条边相等:AB=DE,AC=DF
一边一角相等:∠A=∠D,AB=DE
A
B
C
D
E
F
∠BAC和∠EDF的度数可以不相等,显然不能保证△ABC≌△DEF.
AC和DF长度可以不相等,
显然不能保证△ABC≌△DEF
A
B
C
D
E
F
三、概念剖析
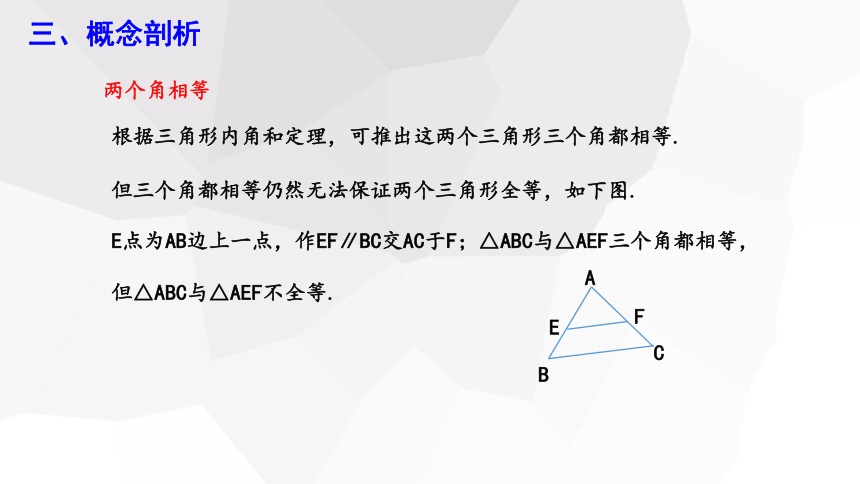
两个角相等
根据三角形内角和定理,可推出这两个三角形三个角都相等.
但三个角都相等仍然无法保证两个三角形全等,如下图.
A
B
C
E
F
E点为AB边上一点,作EF∥BC交AC于F;△ABC与△AEF三个角都相等,但△ABC与△AEF不全等.
三、概念剖析
3.给出三个条件:先任意画一个△ABC,再画一个△DEF.使AB=DE,AC=DF,BD=EF.把画好的△DEF剪下来,放到△ABC上,它们全等吗?
画法如下:
A
B
C
1. 画线段EF=BC.
2. 分别以E、F为圆心,BA、CA为半
径画弧,两弧相交于点D.
3. 连接DE、DF.
D
E
F
结论:△DEF与△ABC完全重合,
∴△ABC≌△DEF.
三、概念剖析
A
B
C
D
E
F
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
通过探究过程我们就可以得出以下结论,用它可以判定两个三角形全等.
三边分别相等的两个三角形全等.(可以简写为“边边边”或“SSS”)
例1.如图,在△ABC中,AB=AC,D为BC中点,△ABD与△ACD是否全等?
∵D为BC中点,∴BD=CD;
在△ABD和△ACD中,
A
B
C
D
AB=AC
BD=CD
AD=AD,
∴△ABD≌△ACD.
解题思路:(1)先找隐含条件:公共边AD;
(2)再找现有条件:AB=AC;
(3)最后找还需准备条件:
BD=CD.
解:△ABD≌△ACD
典型例题
1.如图,已知AB=CB,要使△ABD≌△CBD,则可以添加的一个条件是?
【当堂检测】
AB=CB
AD=CD
BD=BD,
分析:根据题意可知△ABD与△CBD两条边分别相等,如果第三条边也相等,则△ABD≌△CBD.
解:添加AD=CD.
在△ABD和△CBD中,
∴△ABD≌△CBD(SSS).
故可以添加的一个条件是AD=CD
A
B
D
C
三、概念剖析
试一试:盖房子时,在窗框安装好之前,木工师傅常常先在窗框上斜钉
一根木条,为什么要这样做呢?我们来进行下面的操作.
(1)如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的
形状会改变吗?
形状不会改变
(二)三角形的稳定性
三、概念剖析
(2)如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的
形状会改变吗?
形状会发生改变
三、概念剖析
(3)如图,如图,在四边形木架上再钉一根木条,将它的一对不相邻的
顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?
这时,形状不会发生改变
思考:通过以上的操作你能得出什么结论?
结论:通过以上操作可以发现,三角形木架的形状不会改变,而四边形 木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
例2.人站在晃动的公共汽车上,若你分开两腿站立,还需伸出一只手抓住
栏杆才能站稳,这是利用了 .
分析:分开站立,再伸出一只手抓住栏杆,这时,两脚以及抓住栏杆的手可看作三个点,这三个点的连线恰好组成一个三角形,而三角形具有稳定性,这样人就能站稳了.
三角形的稳定性
典型例题
【当堂检测】
2.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变
形,这种做法的根据是( )
A.两点之间,线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
D
【当堂检测】
3.下列物品中利用四边形不稳定性的是( )
A.活动的四边形衣架 B.自行车车架
C.屋顶三角形钢架 D.起重机
A
五、课堂总结
三边分别相等的两个三角形
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
三角形具有稳定性,四边形不具有稳定性.
第四章 三角形
4.3 探索三角形全等的条件
第1课时
1.知道要判定两个三角形全等至少需要三个条件.
2.探究第一种判定三角形全等的方式——边边边.(重点)
3.知道三角形具有稳定性.
一、学习目标
二、新课导入
复习回顾:
1.全等三角形的定义:
2.全等三角形的性质:
能够完全重合的两个三角形叫做全等三角形.
全等三角形对应边相等,对应角相等.
3.已知△ABC≌△DEF,找出其中相等的边与角.
A
B
C
D
E
F
AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠C=∠F.
三、概念剖析
既然我们知道全等三角形三组对应边相等,三组对应角相等.
A
B
C
D
E
F
反之,那么如果在△ABC与△DEF满足三条边分别相等,三组角分别相等,
即AB=DE,BC=EF,AC=DF;∠A=∠D,∠B=∠E,∠C=∠F;那么就能判定
△ABC≌△DEF.
(一)三角形全等的条件
思考:如果只满足以上条件的一部分,那么能保证△ABC≌△DEF吗?
三、概念剖析
1.只给一个条件
一条边相等:AB=DE
一个角相等:∠BAC=∠EDF
A
B
C
D
E
F
C、F两点可以任意变化,
显然不能保证△ABC≌△DEF
A
B
C
D
E
F
不能保证三条边的长度,
显然不能保证△ABC≌△DEF
三、概念剖析
2.只给两个条件
两条边相等:AB=DE,AC=DF
一边一角相等:∠A=∠D,AB=DE
A
B
C
D
E
F
∠BAC和∠EDF的度数可以不相等,显然不能保证△ABC≌△DEF.
AC和DF长度可以不相等,
显然不能保证△ABC≌△DEF
A
B
C
D
E
F
三、概念剖析
两个角相等
根据三角形内角和定理,可推出这两个三角形三个角都相等.
但三个角都相等仍然无法保证两个三角形全等,如下图.
A
B
C
E
F
E点为AB边上一点,作EF∥BC交AC于F;△ABC与△AEF三个角都相等,但△ABC与△AEF不全等.
三、概念剖析
3.给出三个条件:先任意画一个△ABC,再画一个△DEF.使AB=DE,AC=DF,BD=EF.把画好的△DEF剪下来,放到△ABC上,它们全等吗?
画法如下:
A
B
C
1. 画线段EF=BC.
2. 分别以E、F为圆心,BA、CA为半
径画弧,两弧相交于点D.
3. 连接DE、DF.
D
E
F
结论:△DEF与△ABC完全重合,
∴△ABC≌△DEF.
三、概念剖析
A
B
C
D
E
F
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
通过探究过程我们就可以得出以下结论,用它可以判定两个三角形全等.
三边分别相等的两个三角形全等.(可以简写为“边边边”或“SSS”)
例1.如图,在△ABC中,AB=AC,D为BC中点,△ABD与△ACD是否全等?
∵D为BC中点,∴BD=CD;
在△ABD和△ACD中,
A
B
C
D
AB=AC
BD=CD
AD=AD,
∴△ABD≌△ACD.
解题思路:(1)先找隐含条件:公共边AD;
(2)再找现有条件:AB=AC;
(3)最后找还需准备条件:
BD=CD.
解:△ABD≌△ACD
典型例题
1.如图,已知AB=CB,要使△ABD≌△CBD,则可以添加的一个条件是?
【当堂检测】
AB=CB
AD=CD
BD=BD,
分析:根据题意可知△ABD与△CBD两条边分别相等,如果第三条边也相等,则△ABD≌△CBD.
解:添加AD=CD.
在△ABD和△CBD中,
∴△ABD≌△CBD(SSS).
故可以添加的一个条件是AD=CD
A
B
D
C
三、概念剖析
试一试:盖房子时,在窗框安装好之前,木工师傅常常先在窗框上斜钉
一根木条,为什么要这样做呢?我们来进行下面的操作.
(1)如图,将三根木条用钉子钉成一个三角形木架,然后扭动它,它的
形状会改变吗?
形状不会改变
(二)三角形的稳定性
三、概念剖析
(2)如图,将四根木条用钉子钉成一个四边形木架,然后扭动它,它的
形状会改变吗?
形状会发生改变
三、概念剖析
(3)如图,如图,在四边形木架上再钉一根木条,将它的一对不相邻的
顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?
这时,形状不会发生改变
思考:通过以上的操作你能得出什么结论?
结论:通过以上操作可以发现,三角形木架的形状不会改变,而四边形 木架的形状会改变.这就是说,三角形是具有稳定性的图形,而四边形没有稳定性.
例2.人站在晃动的公共汽车上,若你分开两腿站立,还需伸出一只手抓住
栏杆才能站稳,这是利用了 .
分析:分开站立,再伸出一只手抓住栏杆,这时,两脚以及抓住栏杆的手可看作三个点,这三个点的连线恰好组成一个三角形,而三角形具有稳定性,这样人就能站稳了.
三角形的稳定性
典型例题
【当堂检测】
2.如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变
形,这种做法的根据是( )
A.两点之间,线段最短
B.长方形的对称性
C.长方形的四个角都是直角
D.三角形的稳定性
D
【当堂检测】
3.下列物品中利用四边形不稳定性的是( )
A.活动的四边形衣架 B.自行车车架
C.屋顶三角形钢架 D.起重机
A
五、课堂总结
三边分别相等的两个三角形
三角形全等的“SSS”判定:三边分别相等的两个三角形全等.
三角形具有稳定性,四边形不具有稳定性.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
