5.3 简单的轴对称图形 第3课时 课件(共15张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 5.3 简单的轴对称图形 第3课时 课件(共15张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 146.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
第五章 生活中的轴对称
5.3 简单的轴对称图形
第3课时
1.能了解角的轴对称性
2.掌握角平分线的性质,会用尺规作角的平分线(重点)
一、学习目标
二、新课导入
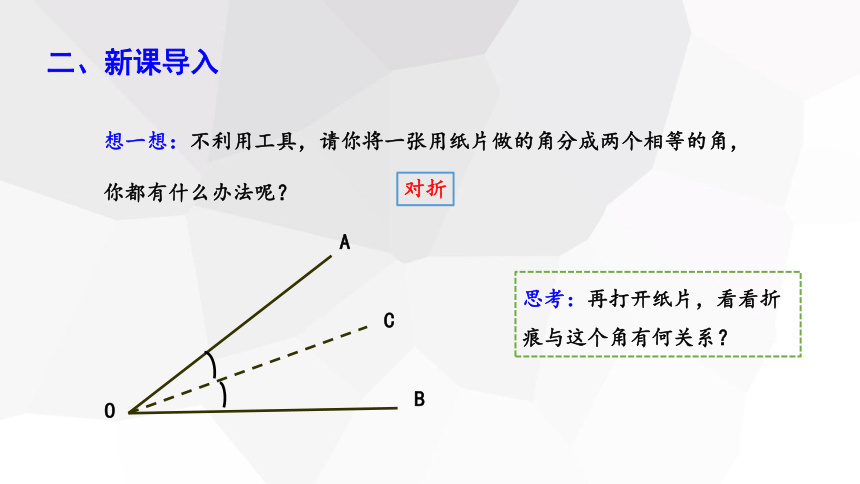
想一想:不利用工具,请你将一张用纸片做的角分成两个相等的角,你都有什么办法呢?
对折
O
B
C
A
思考:再打开纸片,看看折痕与这个角有何关系?
三、概念剖析
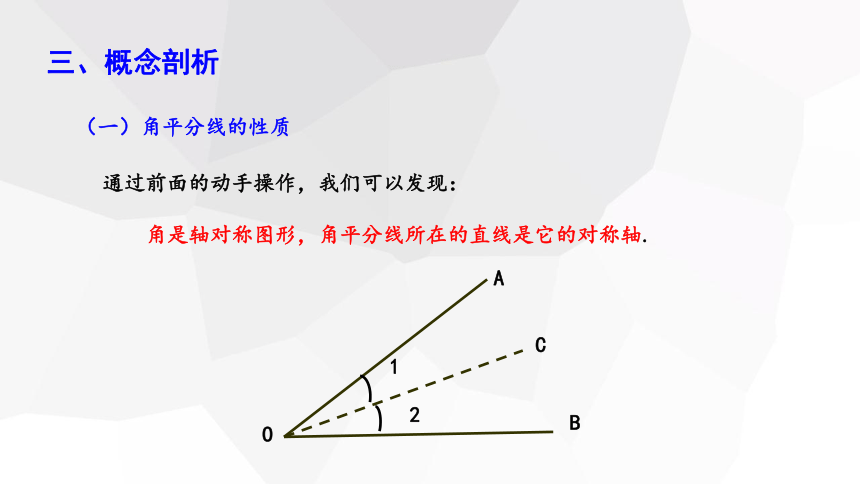
通过前面的动手操作,我们可以发现:
角是轴对称图形,角平分线所在的直线是它的对称轴.
(一)角平分线的性质
O
B
C
A
1
2
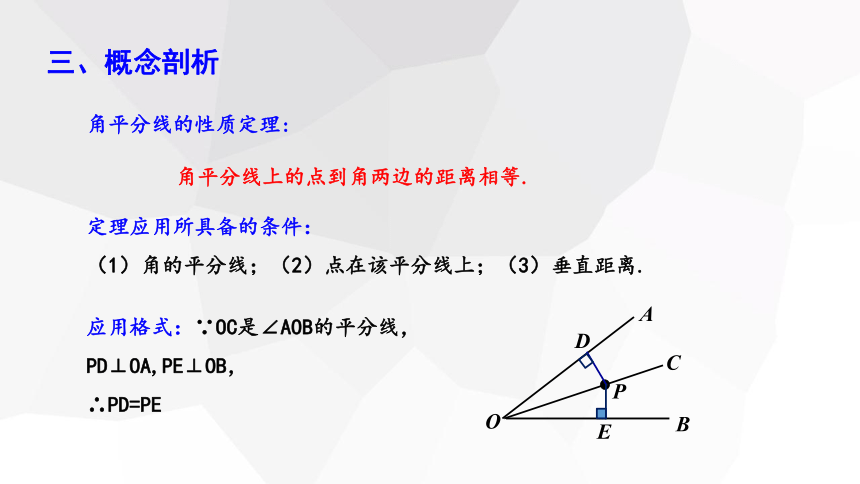
角平分线上的点到角两边的距离相等.
角平分线的性质定理:
定理应用所具备的条件:
(1)角的平分线;(2)点在该平分线上;(3)垂直距离.
应用格式:∵OC是∠AOB的平分线,
PD⊥OA,PE⊥OB,
∴PD=PE
P
A
O
B
C
D
E
三、概念剖析
×
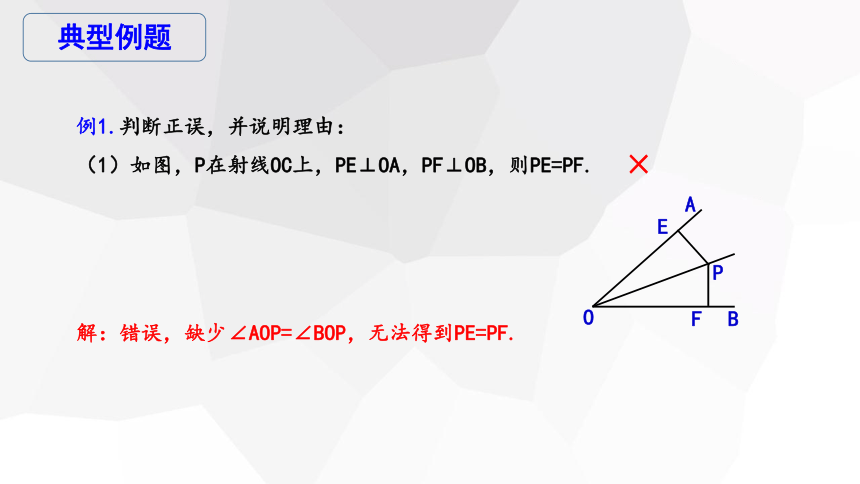
例1.判断正误,并说明理由:
(1)如图,P在射线OC上,PE⊥OA,PF⊥OB,则PE=PF.
解:错误,缺少∠AOP=∠BOP,无法得到PE=PF.
A
O
B
P
E
F
典型例题
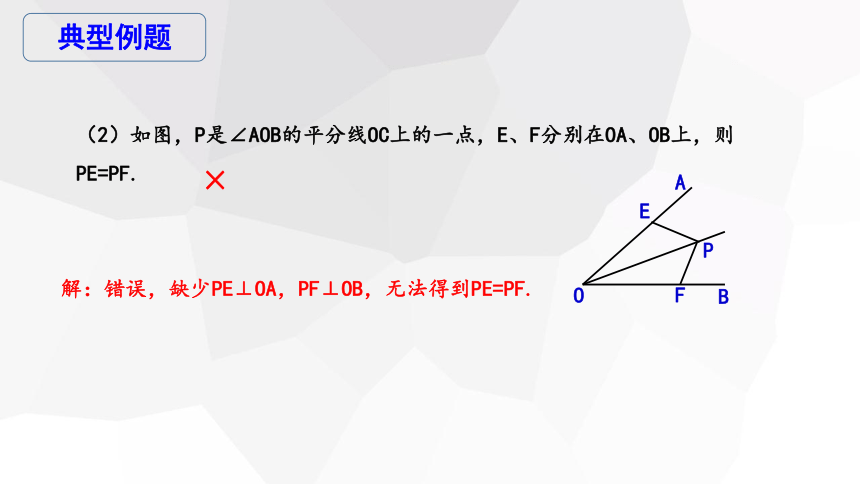
解:错误,缺少PE⊥OA,PF⊥OB,无法得到PE=PF.
(2)如图,P是∠AOB的平分线OC上的一点,E、F分别在OA、OB上,则PE=PF.
×
A
O
B
P
E
F
典型例题
√
(3)如图,在∠AOB的平分线OC上任取一点P,若P到OA的距离为3cm,则P到OB的距离为3cm.
点拨:应用角平分线的性质定理解答即可.
A
O
B
P
E
解:作PF⊥OB交OB于点F,
由题意得,PE⊥OA,PE=3,
∵P在∠AOB的平分线上,且PE⊥OA,PF⊥OB,
∴PE=PF=3.
∴P到OB的距离为3cm.
F
典型例题
【当堂检测】
1.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
3
解:∵AD是∠CAB的平分线,
DC⊥AC,DE⊥AB,
∴DC=DE
又∵BC=8,BD=5,
∴DE=DC=BC-BD=8-5=3
A
B
C
D
E
角的平分线
【当堂检测】
2.如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么线段BE是△ABC的 ,AE+DE= cm.
6
A
B
C
E
D
1
2
解:∵∠1=∠2
∴线段BE是△ABC的角平分线.
∵∠C=90°,DE⊥AB,∠1=∠2,
∴ED=EC,
∴AE+DE=AE+EC=AC=6cm.
点拨:此题主要考查角平分线的性质,正确得出DE=EC是解题关键.
三、概念剖析
(二)尺规作角平分线
尺规作图:
已知∠AOB.求作:∠AOB的平分线.
作法:1.以点O为圆心,任意长为半径作圆弧,与角的两边分别交于M、N两点;
A
B
N
M
P
O
2.分别以M、N为圆心,大于 的长为半径作弧,两条圆弧交于∠AOB内一点P;
3.作射线OP,OP就是所求作的射线.
三、概念剖析
想一想:为什么OP是角平分线呢?请尝试说明理由.
解:在△OMP和△ONP中,
B
A
N
M
P
O
OM=ON,
MP=NP,
OP=OP,
∴ △OMP≌ △ONP,(SSS)
∴∠MOP=∠NOP,即OP平分∠AOB.
典型例题
例2.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
【分析】作∠AOB的角平分线和线段CD的垂直平分线,它们的交点为P点.
解:连接CD,作出CD的垂直平分线;
作出∠AOB的角平分线交CD垂直平分线于一点;
交点即为P点.
P
3.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角平分线上的点到角两边的距离相等
A
【当堂检测】
分析:连接MC、NC,根据SSS得出△ONC ≌ △OMC,即可得出答案.
A
B
M
N
C
O
五、课堂总结
2.角平分线的性质定理:角平分线上的点到这个角的两边距离相等.
1.角是轴对称图形,角平分线所在的直线是它的对称轴.
3.角平分线的作法:尺规作图
第五章 生活中的轴对称
5.3 简单的轴对称图形
第3课时
1.能了解角的轴对称性
2.掌握角平分线的性质,会用尺规作角的平分线(重点)
一、学习目标
二、新课导入
想一想:不利用工具,请你将一张用纸片做的角分成两个相等的角,你都有什么办法呢?
对折
O
B
C
A
思考:再打开纸片,看看折痕与这个角有何关系?
三、概念剖析
通过前面的动手操作,我们可以发现:
角是轴对称图形,角平分线所在的直线是它的对称轴.
(一)角平分线的性质
O
B
C
A
1
2
角平分线上的点到角两边的距离相等.
角平分线的性质定理:
定理应用所具备的条件:
(1)角的平分线;(2)点在该平分线上;(3)垂直距离.
应用格式:∵OC是∠AOB的平分线,
PD⊥OA,PE⊥OB,
∴PD=PE
P
A
O
B
C
D
E
三、概念剖析
×
例1.判断正误,并说明理由:
(1)如图,P在射线OC上,PE⊥OA,PF⊥OB,则PE=PF.
解:错误,缺少∠AOP=∠BOP,无法得到PE=PF.
A
O
B
P
E
F
典型例题
解:错误,缺少PE⊥OA,PF⊥OB,无法得到PE=PF.
(2)如图,P是∠AOB的平分线OC上的一点,E、F分别在OA、OB上,则PE=PF.
×
A
O
B
P
E
F
典型例题
√
(3)如图,在∠AOB的平分线OC上任取一点P,若P到OA的距离为3cm,则P到OB的距离为3cm.
点拨:应用角平分线的性质定理解答即可.
A
O
B
P
E
解:作PF⊥OB交OB于点F,
由题意得,PE⊥OA,PE=3,
∵P在∠AOB的平分线上,且PE⊥OA,PF⊥OB,
∴PE=PF=3.
∴P到OB的距离为3cm.
F
典型例题
【当堂检测】
1.△ABC中, ∠C=90°,AD平分∠CAB,且BC=8,BD=5,则点D到AB的距离是 .
3
解:∵AD是∠CAB的平分线,
DC⊥AC,DE⊥AB,
∴DC=DE
又∵BC=8,BD=5,
∴DE=DC=BC-BD=8-5=3
A
B
C
D
E
角的平分线
【当堂检测】
2.如图,在△ABC中,∠C=90°,DE⊥AB,∠1=∠2,且AC=6cm,那么线段BE是△ABC的 ,AE+DE= cm.
6
A
B
C
E
D
1
2
解:∵∠1=∠2
∴线段BE是△ABC的角平分线.
∵∠C=90°,DE⊥AB,∠1=∠2,
∴ED=EC,
∴AE+DE=AE+EC=AC=6cm.
点拨:此题主要考查角平分线的性质,正确得出DE=EC是解题关键.
三、概念剖析
(二)尺规作角平分线
尺规作图:
已知∠AOB.求作:∠AOB的平分线.
作法:1.以点O为圆心,任意长为半径作圆弧,与角的两边分别交于M、N两点;
A
B
N
M
P
O
2.分别以M、N为圆心,大于 的长为半径作弧,两条圆弧交于∠AOB内一点P;
3.作射线OP,OP就是所求作的射线.
三、概念剖析
想一想:为什么OP是角平分线呢?请尝试说明理由.
解:在△OMP和△ONP中,
B
A
N
M
P
O
OM=ON,
MP=NP,
OP=OP,
∴ △OMP≌ △ONP,(SSS)
∴∠MOP=∠NOP,即OP平分∠AOB.
典型例题
例2.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
【分析】作∠AOB的角平分线和线段CD的垂直平分线,它们的交点为P点.
解:连接CD,作出CD的垂直平分线;
作出∠AOB的角平分线交CD垂直平分线于一点;
交点即为P点.
P
3.用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角平分线上的点到角两边的距离相等
A
【当堂检测】
分析:连接MC、NC,根据SSS得出△ONC ≌ △OMC,即可得出答案.
A
B
M
N
C
O
五、课堂总结
2.角平分线的性质定理:角平分线上的点到这个角的两边距离相等.
1.角是轴对称图形,角平分线所在的直线是它的对称轴.
3.角平分线的作法:尺规作图
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
