4.2 图形的全等 课件 (共16张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 4.2 图形的全等 课件 (共16张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 19:38:28 | ||
图片预览




文档简介
(共16张PPT)
第四章 三角形
4.2 图形的全等
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.理解全等图形的概念,并能找出全等三角形中的对应点、对应边、对应角
2.掌握全等三角形的性质,并应用性质解决相关问题
一、学习目标
二、新课导入
世界上没有完全相同的两片树叶,也没有完全相同的两个人.
但我们在生活中经常能看到形状大小完全相同的图形,你能举一些的例子吗?
同一种剪纸
风扇的叶片
三、概念剖析
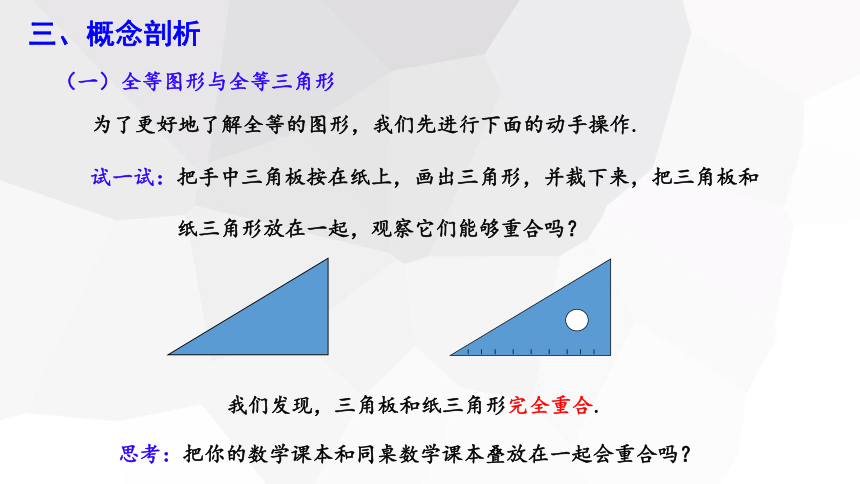
为了更好地了解全等的图形,我们先进行下面的动手操作.
试一试:把手中三角板按在纸上,画出三角形,并裁下来,把三角板和
纸三角形放在一起,观察它们能够重合吗?
我们发现,三角板和纸三角形完全重合.
思考:把你的数学课本和同桌数学课本叠放在一起会重合吗?
(一)全等图形与全等三角形
三、概念剖析
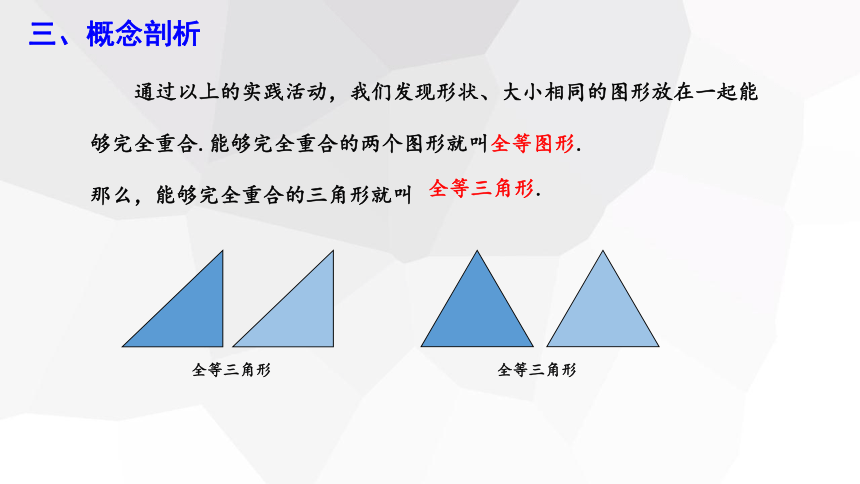
通过以上的实践活动,我们发现形状、大小相同的图形放在一起能
够完全重合.能够完全重合的两个图形就叫全等图形.
那么,能够完全重合的三角形就叫
全等三角形.
全等三角形
全等三角形
三、概念剖析
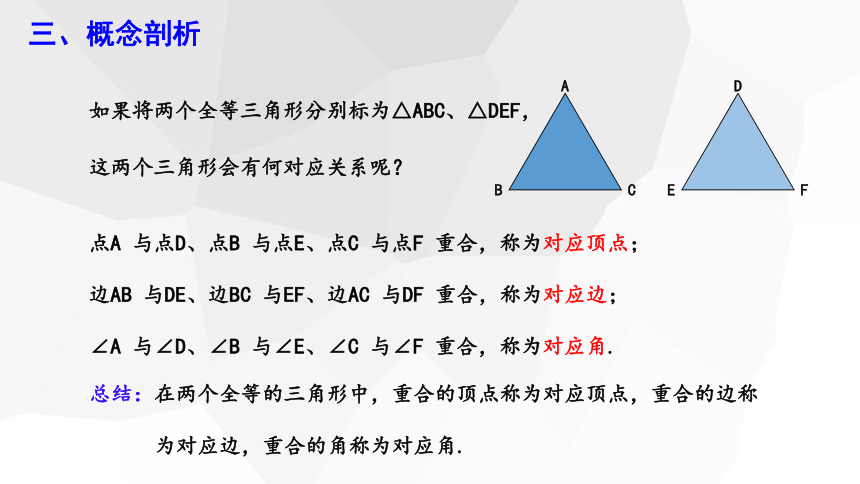
如果将两个全等三角形分别标为△ABC、△DEF,
这两个三角形会有何对应关系呢?
A
B
C
D
E
F
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
总结:在两个全等的三角形中,重合的顶点称为对应顶点,重合的边称
为对应边,重合的角称为对应角.
三、概念剖析
为了方便书写,我们可以用符号表示两个三角形的全等.
例如△ABC与△DEF是全等的,
可以记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
A
B
C
D
E
F
注意:记两个三角形全等时,通常把对应顶点的字母写在对应位置上.
例如,△ABC与△DEF全等,点A 与点D、点B 与点E、点C 与点F为对应
顶点,记作“△ABC ≌△DEF”.
典型例题
例1.如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
1.观察下列几组图形,它们是全等图形吗?
【当堂检测】
(1)
(2)
解:(1)大小不同,(2)形状不同;∴(1)(2)都不是全等图形.
2.如图△ABC≌△ADE,∠C和∠E是对应角,AC和AE是对应边.写出其他
对应边及对应角.
【当堂检测】
A
B
C
D
E
解:其他对应边:AB和AD,BC和DE;
其他对应角:∠BAC和∠DAE,∠ABC和∠ADE.
三、概念剖析
猜想:全等三角形对应边和对应角有什么关系呢?
A
B
C
D
E
F
全等三角形的性质:全等三角形的对应边相等,对应角相等.
应用格式
如图:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
(二)全等三角形的性质
例2.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°, AB=8,EF=5,
求∠DFE的度数与DE的长.
∵在 △ABC中∠A=85°,∠B=60°,
解: ∵△ABC≌△DEF,
∴∠DFE=∠ACB, DE=AB=8;
∴∠ACB=180 °-85°-60°=35°;
∴∠DFE=35 °.
典型例题
3.如图,△ABC≌△EDB,AC=6,AB=8,则AE= .
【当堂检测】
A
B
E
D
C
2
【当堂检测】
4.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
(2)求线段NM及HG的长度;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N, ∠F和∠M, ∠EGF和∠NHM.
(2)∵ △EFG≌△NMH,
∴NM=EF=2.1cm,EG=NH=3.3cm.
∴HG=EG –EH=3.3-1.1=2.2(cm).
四、课堂总结
全等图形
定义:能够完全重合的两个图形.
其他全等图形
性质:对应边相等,对应角相等.
全等三角形
定义:能够完全重合的两个三角形.
第四章 三角形
4.2 图形的全等
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.理解全等图形的概念,并能找出全等三角形中的对应点、对应边、对应角
2.掌握全等三角形的性质,并应用性质解决相关问题
一、学习目标
二、新课导入
世界上没有完全相同的两片树叶,也没有完全相同的两个人.
但我们在生活中经常能看到形状大小完全相同的图形,你能举一些的例子吗?
同一种剪纸
风扇的叶片
三、概念剖析
为了更好地了解全等的图形,我们先进行下面的动手操作.
试一试:把手中三角板按在纸上,画出三角形,并裁下来,把三角板和
纸三角形放在一起,观察它们能够重合吗?
我们发现,三角板和纸三角形完全重合.
思考:把你的数学课本和同桌数学课本叠放在一起会重合吗?
(一)全等图形与全等三角形
三、概念剖析
通过以上的实践活动,我们发现形状、大小相同的图形放在一起能
够完全重合.能够完全重合的两个图形就叫全等图形.
那么,能够完全重合的三角形就叫
全等三角形.
全等三角形
全等三角形
三、概念剖析
如果将两个全等三角形分别标为△ABC、△DEF,
这两个三角形会有何对应关系呢?
A
B
C
D
E
F
点A 与点D、点B 与点E、点C 与点F 重合,称为对应顶点;
边AB 与DE、边BC 与EF、边AC 与DF 重合,称为对应边;
∠A 与∠D、∠B 与∠E、∠C 与∠F 重合,称为对应角.
总结:在两个全等的三角形中,重合的顶点称为对应顶点,重合的边称
为对应边,重合的角称为对应角.
三、概念剖析
为了方便书写,我们可以用符号表示两个三角形的全等.
例如△ABC与△DEF是全等的,
可以记作:“△ABC ≌△DEF”,
读作:“△ABC 全等于△DEF”.
A
B
C
D
E
F
注意:记两个三角形全等时,通常把对应顶点的字母写在对应位置上.
例如,△ABC与△DEF全等,点A 与点D、点B 与点E、点C 与点F为对应
顶点,记作“△ABC ≌△DEF”.
典型例题
例1.如图,若△BOD≌△COE,∠B=∠C,指出这两个全等三角形的对应边;若△ADO≌△AEO,指出这两个三角形的对应角.
解:△BOD与△COE的对应边为:
BO与CO,OD与OE,BD与CE;
△ADO与△AEO的对应角为:
∠DAO与∠EAO,∠ADO与∠AEO,
∠AOD与∠AOE.
1.观察下列几组图形,它们是全等图形吗?
【当堂检测】
(1)
(2)
解:(1)大小不同,(2)形状不同;∴(1)(2)都不是全等图形.
2.如图△ABC≌△ADE,∠C和∠E是对应角,AC和AE是对应边.写出其他
对应边及对应角.
【当堂检测】
A
B
C
D
E
解:其他对应边:AB和AD,BC和DE;
其他对应角:∠BAC和∠DAE,∠ABC和∠ADE.
三、概念剖析
猜想:全等三角形对应边和对应角有什么关系呢?
A
B
C
D
E
F
全等三角形的性质:全等三角形的对应边相等,对应角相等.
应用格式
如图:∵△ABC≌△DEF,
∴AB=DE,BC=EF,AC=DF
∠A=∠D,∠B=∠E,∠C=∠F
(二)全等三角形的性质
例2.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°, AB=8,EF=5,
求∠DFE的度数与DE的长.
∵在 △ABC中∠A=85°,∠B=60°,
解: ∵△ABC≌△DEF,
∴∠DFE=∠ACB, DE=AB=8;
∴∠ACB=180 °-85°-60°=35°;
∴∠DFE=35 °.
典型例题
3.如图,△ABC≌△EDB,AC=6,AB=8,则AE= .
【当堂检测】
A
B
E
D
C
2
【当堂检测】
4.如图,△EFG≌△NMH,EF=2.1cm,EH=1.1cm,NH=3.3cm.
(1)试写出两三角形的对应边、对应角;
(2)求线段NM及HG的长度;
解:(1)对应边有EF和NM,FG和MH,EG和NH;
对应角有∠E和∠N, ∠F和∠M, ∠EGF和∠NHM.
(2)∵ △EFG≌△NMH,
∴NM=EF=2.1cm,EG=NH=3.3cm.
∴HG=EG –EH=3.3-1.1=2.2(cm).
四、课堂总结
全等图形
定义:能够完全重合的两个图形.
其他全等图形
性质:对应边相等,对应角相等.
全等三角形
定义:能够完全重合的两个三角形.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
