第四章 三角形 复习课课件(共26张PPT) 2023-2024学年初中数学北师大版七年级下册
文档属性
| 名称 | 第四章 三角形 复习课课件(共26张PPT) 2023-2024学年初中数学北师大版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 964.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第四章 三角形
复习课
1.知道三角形的相关概念,边角关系以及性质
2.掌握三角形不同的判定条件,会利用尺规作全等三角形
3.会构建全等三角形,能用三角形全等解决相关实际问题
一、学习目标
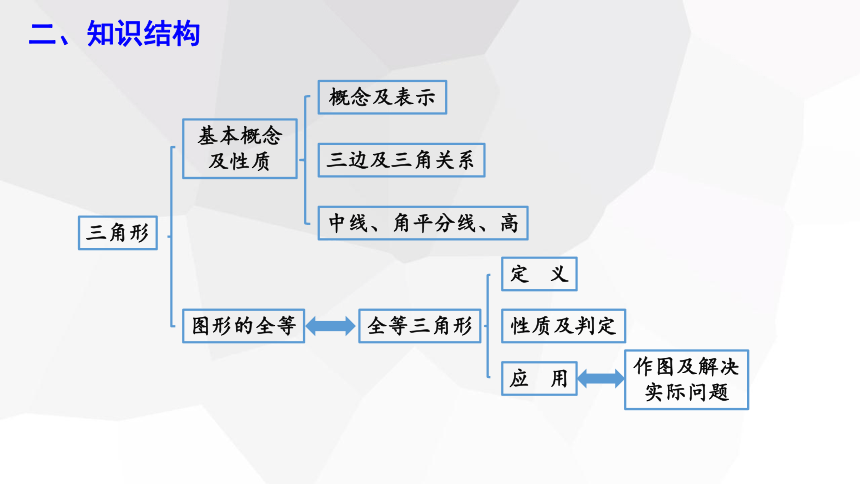
二、知识结构
全等三角形
定义
性质及判定
应用
基本概念及性质
概念及表示
三边及三角关系
中线、角平分线、高
三角形
图形的全等
作图及解决实际问题
1.与三角有关的线段
三角形的概念:
三角形两边的和大于第三边,三角形两边的差小于第三边.
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,用符号△表示;
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之
间的线段;
A
B
C
边
内角
顶点
边的关系:
高:
三、知识梳理
在三角形中,连接一个顶点与它对边中点的线段;
在三角形中,一个内角的角平分线与它的对边相交,这个角的
顶点与交点之间的线段.
在一个三角形中,三条中线交于一点(重心),三条高交于一点(垂心),三条内角平分线交于一点(内心).
中线:
角平分线:
三、知识梳理
2.与三角形有关的角
相邻两边组成的角;三角形的内角和等于180 °.
直角三角形的两个锐角互余.
内角:
直角三角形的性质:
三、知识梳理
三、知识梳理
3.全等形
全等形的定义:
能够完全重合的两个三角形就叫全等三角形.
完全重合的两个图形就叫全等形.
两个全等三角形对应边相等,对应角相等.
全等三角形的定义:
全等三角形的性质:
全等三角形
4.全等三角形的判定
有三边对应相等的两个三角形全等(简写:“边边边”或“SSS”).
判定1:“SSS”
A
B
C
D
E
F
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
三、知识梳理
三角形具有稳定性,四边形具有不稳定性.
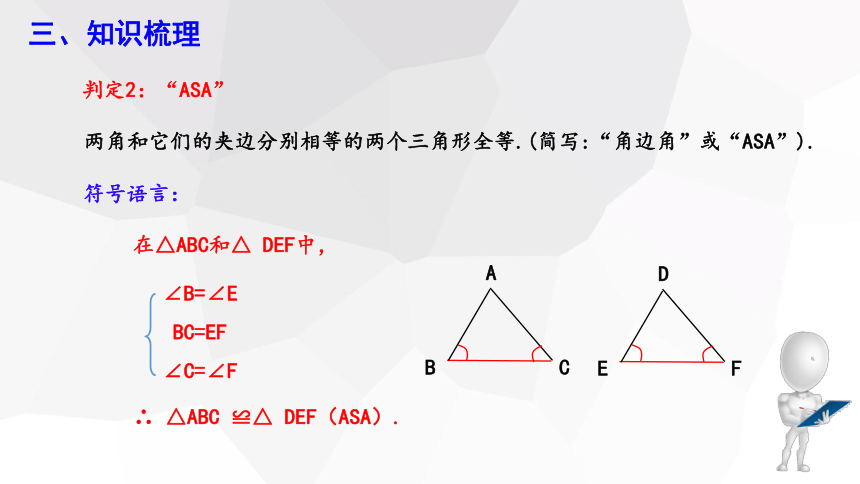
两角和它们的夹边分别相等的两个三角形全等.(简写:“角边角”或“ASA”).
判定2:“ASA”
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(ASA).
∠B=∠E
BC=EF
∠C=∠F
A
B
C
D
E
F
三、知识梳理
两角和其中一个角的对边分别相等的两个三角形全等.(“角角边”或“AAS”)
判定3:“AAS”
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(AAS).
∠A=∠D
∠B=∠E
BC=EF
A
B
C
D
E
F
三、知识梳理
两边和它们的夹角分别相等的两个三角形全等.(简写:“边角边”或“SAS”).
判定4:“SAS”
A
B
C
D
E
F
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
AB=DE
∠A=∠D
AC=DF
三、知识梳理
5.三角形全等的应用
(1)已知三角形的两边及其夹角,求作这个三角形.
(2)已知三角形的两角及其夹边,求作这个三角形.
(3)已知三角形的三边,求作这个三角形.
(1)构造全等三角形;(2)证明两条线段相等;
(3)计算该线段的长度(大多数情况下已知另一条线段的长度,不必计算).
尺规作三角形:
利用三角形全等测距离:
三、知识梳理
例1.在△ABC中的AB、BC两边长分别是2和7,且BC为最长边;若AC边长为整数,求AC边长.
A
B
C
解:设AC边长为x,
根据题意得:x+2>7即x>5,x<7.
所以x的值大于5小于7.
AC边长为整数,所以x只能取6,故AC边长为6.
分析:根据两条短边之和大于第三边即可解答.
(一)与三角形有关的线段
典型例题
(1)过点A画出它的高、过点B作出其中线、过点C作出其角平分线.
例2.如图△ABC的三个顶点分别为A、B、C.
A
B
C
A
B
C
A
B
C
D
AD⊥BC
A0=C0
∠ACE=∠BCE
0
E
典型例题
(2)BO为△ABC中线,已知BC-AB=4cm, △B0C的周长为16cm,求△A0B的周长.
A
B
C
0
解:∵BO是△ABC的中线,∴A0=C0 .
∵BC-AB=4cm,
∴(BC+BO+CO)-(AB+A0+B0)=4cm,
∴ △B0C与△A0B的周长差是4cm;
又∵ △B0C的周长为16cm,
∴ △A0B的周长=16-4=12(cm).
典型例题
1.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
【当堂检测】
【分析】由BD是△ABC的中线,AD=2,可得AD=DC,故AC=4;又AB+BC=5,∴△ABC的周长可求.
解:因为BD是△ABC的中线,
所以点D是AC的中点,
所以AC=2AD=4,
所以△ABC的周长为AB+BC+AC=5+4=9.
例3.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,且相交
于点P.已知∠APE=55°,∠AEP=80°,∠B的度数是多少?
(二)与三角形有关的角
A
B
C
D
E
P
解:∵AD⊥BC,∴∠PDC=90°,
∵∠APE=55°,∠AEP=80°,
∴∠PAE=180°-(∠APE+∠AEP)=45°,
∴∠B=90°-45°=45°,
故∠B的度数是为45°.
典型例题
2.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,
已知∠D=29°,则∠1的度数为多少?
【当堂检测】
A
B
C
D
1
(
解:∵CD∥AB,∠D=29°,∴∠ABD=∠D=29°
又∵BD平分∠ABC,∴∠ABC=2∠ABD=58°,
∵∠BAC=90°,
∴在△ABC中,∠1=180°-(∠ABC+∠BAC)=32°
例4.如图,△ABC≌△CDE,A、D、C在一条直线上,且∠A=60°,
∠E=30°,求∠ECB的度数.
(三)全等三角形的性质与判定
A
B
E
D
C
解: ∵△ABC≌△CDE,
∴∠DCE=∠A=60°,∠ACB=∠E=30°,
∵∠ECB=∠DCE-∠ACB,
∴∠ECB=60°-30°=30°,故∠ECB的度数为30°.
典型例题
例5.如图,∠A=∠D,∠ACB=∠DBC,试说明:△AOB≌△DOC.
A
B
C
D
O
∴△ABC≌△DBC(AAS).
解:
∠ACB=∠DBC
BC=CB
∠A=∠D
在△ABC和△DCB中,
∴AB=DC.
在△AOB和△DOC中,
∠AOB=∠DOC
AB=DC
∠A=∠D
∴△AOB≌△DOC(AAS).
典型例题
3.如图, △ADE≌△BCE, AC=2 cm,AB=7cm,求CD的长.
【当堂检测】
A
B
C
D
E
解: ∵ △ADE≌△BCE,
∴ AD=BC.
∵ AC=AD-CD,BD=BC-CD,
∴ BD=AC=2cm.
∴ CD=AB-AC-BD=7-2-2=3(cm).
4.如图,已知OA=OB,OC=OD,连接AD,BC,两线相交于点P,连接OP.
(1)图中有 对全等三角形;
(2)请选择其中一对全等三角形给予说明.
【当堂检测】
O
D
B
A
P
C
解:(1)图中有4对全等三角形:△AOD与△BOC,
△APC与△BPD,△AOP与△BOP,△POC与△POD.
(2)在△AOD与△BOC中,
∴△AOD≌△BOC(SAS),
∴∠C=∠D,
∵OA=OB,OC=OD,
∴AC=BD,
OA=OB
∠AOD=∠BOC
OD=OC,
4
【当堂检测】
O
D
B
A
P
C
在△POC与△POD中,
在△APC与△BPD中,
∴△APC≌△BPD(AAS),
∴AP=BP,
在△AOP与△BOP中,
∴△AOP≌△BOP(SSS),
∴∠AOP=∠BOP,
∠C=∠D
∠APC=∠BPD
AC=BD
OA=OB
OP=OP
AP=BP
OC=OD
∠COP=∠DOP
OP=OP
∴△POC≌△POD(SAS).
说明其中一对全等三角形即可
例6.如图,树AB与树CD之间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,且两条视线的夹角正好为90°,EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,求小华行走到点E的时间.
(四)三角形全等的应用
解:∵∠AED=90°,∴∠AEB+∠DEC=90°.
∵∠ABE=90°,∴∠A+∠AEB=90°.∴∠A=∠DEC,
在△ABE和△ECD中,∠B=∠C ,∠A=∠DEC ,AE=ED
∴△ABE≌△ECD(AAS),∴EC=AB=5m.
∵BC=13m,∴BE=8m.
∴小华走的时间是8÷1=8(s).
典型例题
5.如图,两根长12m的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何来检验旗杆是否垂直于地面?请说明理由.
【当堂检测】
解:用卷尺测量出BD、CD,看它们是否相等,若BD=CD,则AD⊥BC.
理由如下:∵在△ABD和△ACD中,
AB=AC ,BD=CD ,AD=AD ,
∴△ABD≌△ACD(SSS),∴∠ADB=∠ADC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
四、课堂总结
全等三角形
定义
性质及判定
应用
基本概念及性质
概念及表示
三边及三角关系
中线、角平分线、高
三角形
图形的全等
作图及解决实际问题
第四章 三角形
复习课
1.知道三角形的相关概念,边角关系以及性质
2.掌握三角形不同的判定条件,会利用尺规作全等三角形
3.会构建全等三角形,能用三角形全等解决相关实际问题
一、学习目标
二、知识结构
全等三角形
定义
性质及判定
应用
基本概念及性质
概念及表示
三边及三角关系
中线、角平分线、高
三角形
图形的全等
作图及解决实际问题
1.与三角有关的线段
三角形的概念:
三角形两边的和大于第三边,三角形两边的差小于第三边.
由不在同一条直线上的三条线段首尾顺次相接所组成的图形,用符号△表示;
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之
间的线段;
A
B
C
边
内角
顶点
边的关系:
高:
三、知识梳理
在三角形中,连接一个顶点与它对边中点的线段;
在三角形中,一个内角的角平分线与它的对边相交,这个角的
顶点与交点之间的线段.
在一个三角形中,三条中线交于一点(重心),三条高交于一点(垂心),三条内角平分线交于一点(内心).
中线:
角平分线:
三、知识梳理
2.与三角形有关的角
相邻两边组成的角;三角形的内角和等于180 °.
直角三角形的两个锐角互余.
内角:
直角三角形的性质:
三、知识梳理
三、知识梳理
3.全等形
全等形的定义:
能够完全重合的两个三角形就叫全等三角形.
完全重合的两个图形就叫全等形.
两个全等三角形对应边相等,对应角相等.
全等三角形的定义:
全等三角形的性质:
全等三角形
4.全等三角形的判定
有三边对应相等的两个三角形全等(简写:“边边边”或“SSS”).
判定1:“SSS”
A
B
C
D
E
F
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
三、知识梳理
三角形具有稳定性,四边形具有不稳定性.
两角和它们的夹边分别相等的两个三角形全等.(简写:“角边角”或“ASA”).
判定2:“ASA”
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(ASA).
∠B=∠E
BC=EF
∠C=∠F
A
B
C
D
E
F
三、知识梳理
两角和其中一个角的对边分别相等的两个三角形全等.(“角角边”或“AAS”)
判定3:“AAS”
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(AAS).
∠A=∠D
∠B=∠E
BC=EF
A
B
C
D
E
F
三、知识梳理
两边和它们的夹角分别相等的两个三角形全等.(简写:“边角边”或“SAS”).
判定4:“SAS”
A
B
C
D
E
F
符号语言:
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
AB=DE
∠A=∠D
AC=DF
三、知识梳理
5.三角形全等的应用
(1)已知三角形的两边及其夹角,求作这个三角形.
(2)已知三角形的两角及其夹边,求作这个三角形.
(3)已知三角形的三边,求作这个三角形.
(1)构造全等三角形;(2)证明两条线段相等;
(3)计算该线段的长度(大多数情况下已知另一条线段的长度,不必计算).
尺规作三角形:
利用三角形全等测距离:
三、知识梳理
例1.在△ABC中的AB、BC两边长分别是2和7,且BC为最长边;若AC边长为整数,求AC边长.
A
B
C
解:设AC边长为x,
根据题意得:x+2>7即x>5,x<7.
所以x的值大于5小于7.
AC边长为整数,所以x只能取6,故AC边长为6.
分析:根据两条短边之和大于第三边即可解答.
(一)与三角形有关的线段
典型例题
(1)过点A画出它的高、过点B作出其中线、过点C作出其角平分线.
例2.如图△ABC的三个顶点分别为A、B、C.
A
B
C
A
B
C
A
B
C
D
AD⊥BC
A0=C0
∠ACE=∠BCE
0
E
典型例题
(2)BO为△ABC中线,已知BC-AB=4cm, △B0C的周长为16cm,求△A0B的周长.
A
B
C
0
解:∵BO是△ABC的中线,∴A0=C0 .
∵BC-AB=4cm,
∴(BC+BO+CO)-(AB+A0+B0)=4cm,
∴ △B0C与△A0B的周长差是4cm;
又∵ △B0C的周长为16cm,
∴ △A0B的周长=16-4=12(cm).
典型例题
1.如图所示,BD是△ABC的中线,AD=2,AB+BC=5,求△ABC的周长.
【当堂检测】
【分析】由BD是△ABC的中线,AD=2,可得AD=DC,故AC=4;又AB+BC=5,∴△ABC的周长可求.
解:因为BD是△ABC的中线,
所以点D是AC的中点,
所以AC=2AD=4,
所以△ABC的周长为AB+BC+AC=5+4=9.
例3.如图,在△ABC中,AD是BC边上的高线,CE是一条角平分线,且相交
于点P.已知∠APE=55°,∠AEP=80°,∠B的度数是多少?
(二)与三角形有关的角
A
B
C
D
E
P
解:∵AD⊥BC,∴∠PDC=90°,
∵∠APE=55°,∠AEP=80°,
∴∠PAE=180°-(∠APE+∠AEP)=45°,
∴∠B=90°-45°=45°,
故∠B的度数是为45°.
典型例题
2.如图,在△ABC中,∠BAC=90°,BD平分∠ABC,CD∥AB交BD于点D,
已知∠D=29°,则∠1的度数为多少?
【当堂检测】
A
B
C
D
1
(
解:∵CD∥AB,∠D=29°,∴∠ABD=∠D=29°
又∵BD平分∠ABC,∴∠ABC=2∠ABD=58°,
∵∠BAC=90°,
∴在△ABC中,∠1=180°-(∠ABC+∠BAC)=32°
例4.如图,△ABC≌△CDE,A、D、C在一条直线上,且∠A=60°,
∠E=30°,求∠ECB的度数.
(三)全等三角形的性质与判定
A
B
E
D
C
解: ∵△ABC≌△CDE,
∴∠DCE=∠A=60°,∠ACB=∠E=30°,
∵∠ECB=∠DCE-∠ACB,
∴∠ECB=60°-30°=30°,故∠ECB的度数为30°.
典型例题
例5.如图,∠A=∠D,∠ACB=∠DBC,试说明:△AOB≌△DOC.
A
B
C
D
O
∴△ABC≌△DBC(AAS).
解:
∠ACB=∠DBC
BC=CB
∠A=∠D
在△ABC和△DCB中,
∴AB=DC.
在△AOB和△DOC中,
∠AOB=∠DOC
AB=DC
∠A=∠D
∴△AOB≌△DOC(AAS).
典型例题
3.如图, △ADE≌△BCE, AC=2 cm,AB=7cm,求CD的长.
【当堂检测】
A
B
C
D
E
解: ∵ △ADE≌△BCE,
∴ AD=BC.
∵ AC=AD-CD,BD=BC-CD,
∴ BD=AC=2cm.
∴ CD=AB-AC-BD=7-2-2=3(cm).
4.如图,已知OA=OB,OC=OD,连接AD,BC,两线相交于点P,连接OP.
(1)图中有 对全等三角形;
(2)请选择其中一对全等三角形给予说明.
【当堂检测】
O
D
B
A
P
C
解:(1)图中有4对全等三角形:△AOD与△BOC,
△APC与△BPD,△AOP与△BOP,△POC与△POD.
(2)在△AOD与△BOC中,
∴△AOD≌△BOC(SAS),
∴∠C=∠D,
∵OA=OB,OC=OD,
∴AC=BD,
OA=OB
∠AOD=∠BOC
OD=OC,
4
【当堂检测】
O
D
B
A
P
C
在△POC与△POD中,
在△APC与△BPD中,
∴△APC≌△BPD(AAS),
∴AP=BP,
在△AOP与△BOP中,
∴△AOP≌△BOP(SSS),
∴∠AOP=∠BOP,
∠C=∠D
∠APC=∠BPD
AC=BD
OA=OB
OP=OP
AP=BP
OC=OD
∠COP=∠DOP
OP=OP
∴△POC≌△POD(SAS).
说明其中一对全等三角形即可
例6.如图,树AB与树CD之间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,且两条视线的夹角正好为90°,EA=ED.已知大树AB的高为5m,小华行走的速度为1m/s,求小华行走到点E的时间.
(四)三角形全等的应用
解:∵∠AED=90°,∴∠AEB+∠DEC=90°.
∵∠ABE=90°,∴∠A+∠AEB=90°.∴∠A=∠DEC,
在△ABE和△ECD中,∠B=∠C ,∠A=∠DEC ,AE=ED
∴△ABE≌△ECD(AAS),∴EC=AB=5m.
∵BC=13m,∴BE=8m.
∴小华走的时间是8÷1=8(s).
典型例题
5.如图,两根长12m的绳子,一端系在旗杆上的同一位置,另一端分别固定在地面上的两个木桩上(绳结处的误差忽略不计),现在只有一把卷尺,如何来检验旗杆是否垂直于地面?请说明理由.
【当堂检测】
解:用卷尺测量出BD、CD,看它们是否相等,若BD=CD,则AD⊥BC.
理由如下:∵在△ABD和△ACD中,
AB=AC ,BD=CD ,AD=AD ,
∴△ABD≌△ACD(SSS),∴∠ADB=∠ADC,
又∵∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
四、课堂总结
全等三角形
定义
性质及判定
应用
基本概念及性质
概念及表示
三边及三角关系
中线、角平分线、高
三角形
图形的全等
作图及解决实际问题
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
