第一章 复习课(27页) 课件 2023-2024学年初中数学北师大版七年级下册(26张PPT)
文档属性
| 名称 | 第一章 复习课(27页) 课件 2023-2024学年初中数学北师大版七年级下册(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 249.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 19:44:36 | ||
图片预览








文档简介
(共26张PPT)
第一章 整式的乘除
复习课
1.能掌握幂的相关运算及其性质
2.能掌握整式的乘除运算法则及混合运算的顺序
3.能掌握乘法公式,能运用乘法公式化简整式运算
一、学习目标
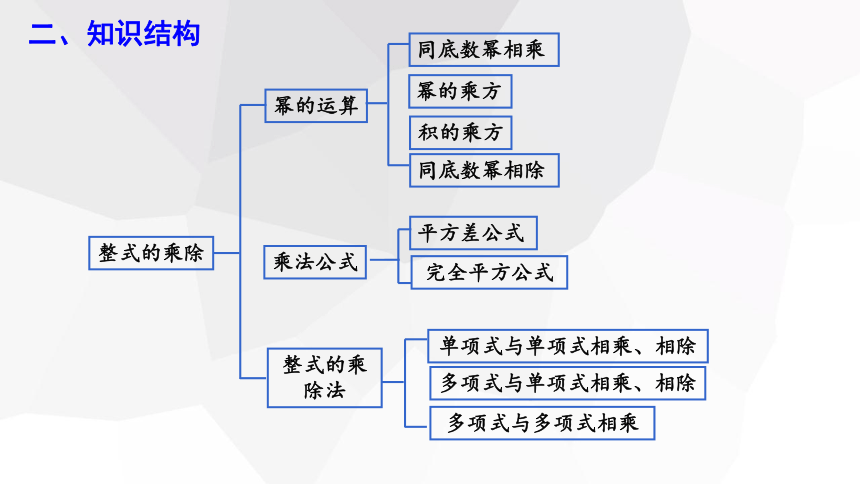
二、知识结构
幂的运算
乘法公式
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
整式的乘除法
单项式与单项式相乘、相除
多项式与多项式相乘
同底数幂相乘
幂的乘方
同底数幂相除
三、知识梳理
1.幂的运算性质
当m,n是正整数时,
(1)同底数幂的乘法:am·an = am+n ;
(2)同底数幂的除法:am÷an = am-n ;a0=1(a≠0)
(3)幂的乘方: (am )n = amn ;
(4)积的乘方: (ab)n = anbn .
(5)负整数指数幂: (a≠0,p是正整数).
2.整式的乘、除法则
三、知识梳理
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只
在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)单项式与单项式相乘的法则:
用单项式去乘多项式的每一项,再把所得的积相加.
(2)单项式与多项式相乘的法则:
先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(3)多项式与多项式相乘的法则:
三、知识梳理
(4)单项式除以单项式的法则:
单项式相除,把系数与同底数幂分别相除作为商的因式,对于
只在被除式里含有的字母,则连同它的指数作为商的一个因式.
(5)多项式除以单项式的法则:
多项除以单项式,先把这个多项式的每一项除以这个单项式,
再把所得的商相加.
3.乘法公式
三、知识梳理
(1)平方差公式:
(a+b)(a-b)=a2-b2
(2)完全平方公式:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
四、典型例题
(一)幂的运算性质
例1.计算(2a)3(b3)2÷4a3b4.
分析:幂的混合运算中,先算乘方,再算乘除.
解:原式=8a3b6 ÷4a3b4
=2a3-3b6-4
=2b2.
四、典型例题
例2.计算(-8)2020 ×(0.125)2019.
分析:此题可先用同底数幂的乘法的逆运算,将(-8)2020化为(-8)×(-8)2019,
再用积的乘方的性质的逆运算进行计算.
解:原式=(-8)×(-8)2019 ×(0.125)2019
=(-8)[(-8) ×0.125]2019
=(-8)×(-1)2019
=8.
小结:运用幂的运算公式,可将问题化繁为简,
负数乘方结果的符号,奇次方得负,偶次方得正.
四、典型例题
归纳总结:幂的运算性质包括同底数幂的乘法、幂的乘方、积的乘方及
同底数幂的除法.这四种运算性质贯穿全章,是整式乘除及因式分解的
基础.其逆向运用可以使一些计算简便,从而培养一定的计算技巧,达
到学以致用的目的.
【当堂检测】
2.(1)若∣p+3∣=(-2019)0,则p= ;
(2)若(x-2)0=1,则x应满足的条件是 .
1.下列计算不正确的是( )
A.2a3 ÷a=2a2 B. (-a3)2=a6
C. a4 ·a3=a7 D. a2·a4=a8
-4或-2
x≠2
D
解析:a2·a4=a2+4=a6,故D选项错误.
解析:任何不等于0的数的0次幂都等于1,;故(1)中∣p+3∣=1,(2)中x-2≠0.
【当堂检测】
3. (1)计算:0.252019 ×(-4)2019-8100 ×0.5301;
(2)比较大小:420与1510.
解:(1)原式=[0.25 ×(-4)]2019-(23)100 ×0.5300 ×0.5
(2) ∵420=(42)10=1610,1610>1510, ∴420>1510.
=-1-(2 ×0.5)300 ×0.5
=-1-0.5
=-1.5;
【当堂检测】
4.已知10x=5,10y=6,求103x+2y的值.
103x+2y
=103x 102y
=(10x)3 (10y)2
=53×62
=4500.
解:
四、典型例题
例3.计算:[x(x2y2-xy)-y(x2-x3y)] ÷3x2y,其中x=1,y=3.
分析:在计算整式的加、减、乘、除、乘方的运算中,一要注意运算顺序;
二要熟练正确地运用运算法则.
解:原式=(x3y2-x2y-x2y+x3y2)÷3x2y
当x=1,y=3时,原式= .
=(2x3y2-2x2y) ÷3x2y
= - .
(二)整式的运算
四、典型例题
归纳总结:整式的乘除法主要包括单项式乘以单项式、单项式乘以多项式、
多项式乘以多项式以及单项式除以单项式、多项式除以单项式,其中单项式
乘以单项式是整式乘除的基础,必须熟练掌握它们的运算法则,整式的混合
运算,要按照先算乘方,再算乘除,最后算加减的顺序进行,有括号的要算
括号里的.
【当堂检测】
5.计算:(1)(2a+5b)(a-3b);(2)(x+1)(x2-x+1);
(3)(3x-2y)(y-3x)-(2x-y)(3x+y).
解:(1)原式=2a2-6ab+5ab-15b2
=2a2-ab-15b2.
(2)原式=x3-x2+x+x2-x+1
=x3+1.
(3)原式=(-9x2+9xy-2y2)-(6x2-xy-y2)
=-15x2+10xy-y2.
【当堂检测】
6.(1)一个长方形的面积是a2-2ab+a,宽为a,则长方形的长为 ;
(2)已知多项式2x3-4x2-1除以一个多项式A,得商为2x,余式为x-1,
则这个多项式A是 .
a-2b+1
x2-2x-
四、典型例题
(三)整式的乘法公式的运用
例4.先化简再求值:[(x-y)2+(x+y)(x-y)] ÷2x,其中x=3,y=1.5.
分析:运用平方差公式和完全平方公式,先计算括号内的,再计算整式 的除法运算.
解:原式=(x2-2xy+y2+x2-y2) ÷2x
=(2x2-2xy) ÷2x
=x-y.
当x=3,y=1.5时,原式=3-1.5=1.5.
四、典型例题
归纳总结:整式的乘法公式包括平方差公式和完全平方公式,而完全平方
公式又分为两个:两数和的完全平方公式和两数差的完全平方公式,在计
算多项式的乘法时,对于符合这三个公式结构特征的式子,运用公式可减
少运算量,提高解题速度.
【当堂检测】
8.(1)求方程(x-1)2-(x-1)(x+1)+3(1-x)=0的解;
(2)已知x2+9y2+4x-6y+5=0,求xy的值.
解:(1)原方程可化为-5x+5=0,解得x=1.
(2) ∵x2+9y2+4x-6y+5=0,
∴(x2+4x+4)+(9y2-6y+1)=0,
∴(x+2)2+(3y-1)2=0.
∴x+2=0,3y-1=0,解得x=-2, y= ,
【当堂检测】
9.计算:[(x+2y)2-(x+y)(3x-y)-5y2]÷2x.
解:原式=(x2+4xy+4y2-3x2+xy-3xy+y2-5y2)÷2x
=(-2x2+2xy)÷2x
=-x+y.
四、典型例题
(四)实际问题转化为数学模型
解析:图(1)的阴影 部分面积是两个正方形的面积差(a2-b2),图(2)梯形的
面积是(2a+2b)(a-b)÷2=(a+b)(a-b),根据面积相等,得a2-b2=(a+b)(a-b).
例6.如图所示,在边长为a的正方形中剪去边长为b的小正方形,把剩下的部分
拼成梯形,分别计算这两个图形的阴影部分的面积,验证公式是 .
a2-b2=(a+b)(a-b)
b
a
a
a
a
b
b
b
b
a-b
b
(2)
(1)
归纳总结:本章中数形结合思想主要体现在根据给定的图形写出一个代数恒等式或根据代数式画出几何图形. 由几何图形得到代数恒等式时,需要用不同的方法表示几何图形的面积,然后得出代数恒等式;由代数恒等式画图时,关键在于合理拼接,往往是相等的边拼到一起.
四、典型例题
【当堂检测】
10. 我们已知道,完全平方公式可以用平面几何图形的面积来表示,
实际上还有一个代数恒等式也可以用这种形式来表示,例如
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①和图②等图形的面积表示.
a
a
a
b
b
ab
ab
ab
a2
a2
b2
图①
b2
a2
a2
ab
ab
ab
a
a
a
b
b
图②
(2)请画一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
(1)请写出图③所表示的代数恒等式;
b
b
a
a
b
a
ab
ab
ab
ab
ab
a2
a2
b2
b2
图③
解:(2a+b)(a+2b)=2a2+5ab+2b2;
如图④.
图④
a2
b
a
ab
ab
ab
ab
b2
b2
b2
a
b
b
b
【当堂检测】
五、课堂总结
幂的运算
乘法公式
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
整式的乘除法
单项式与单项式相乘、相除
多项式与多项式相乘
同底数幂相乘
幂的乘方
同底数幂相除
第一章 整式的乘除
复习课
1.能掌握幂的相关运算及其性质
2.能掌握整式的乘除运算法则及混合运算的顺序
3.能掌握乘法公式,能运用乘法公式化简整式运算
一、学习目标
二、知识结构
幂的运算
乘法公式
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
整式的乘除法
单项式与单项式相乘、相除
多项式与多项式相乘
同底数幂相乘
幂的乘方
同底数幂相除
三、知识梳理
1.幂的运算性质
当m,n是正整数时,
(1)同底数幂的乘法:am·an = am+n ;
(2)同底数幂的除法:am÷an = am-n ;a0=1(a≠0)
(3)幂的乘方: (am )n = amn ;
(4)积的乘方: (ab)n = anbn .
(5)负整数指数幂: (a≠0,p是正整数).
2.整式的乘、除法则
三、知识梳理
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只
在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)单项式与单项式相乘的法则:
用单项式去乘多项式的每一项,再把所得的积相加.
(2)单项式与多项式相乘的法则:
先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(3)多项式与多项式相乘的法则:
三、知识梳理
(4)单项式除以单项式的法则:
单项式相除,把系数与同底数幂分别相除作为商的因式,对于
只在被除式里含有的字母,则连同它的指数作为商的一个因式.
(5)多项式除以单项式的法则:
多项除以单项式,先把这个多项式的每一项除以这个单项式,
再把所得的商相加.
3.乘法公式
三、知识梳理
(1)平方差公式:
(a+b)(a-b)=a2-b2
(2)完全平方公式:
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
四、典型例题
(一)幂的运算性质
例1.计算(2a)3(b3)2÷4a3b4.
分析:幂的混合运算中,先算乘方,再算乘除.
解:原式=8a3b6 ÷4a3b4
=2a3-3b6-4
=2b2.
四、典型例题
例2.计算(-8)2020 ×(0.125)2019.
分析:此题可先用同底数幂的乘法的逆运算,将(-8)2020化为(-8)×(-8)2019,
再用积的乘方的性质的逆运算进行计算.
解:原式=(-8)×(-8)2019 ×(0.125)2019
=(-8)[(-8) ×0.125]2019
=(-8)×(-1)2019
=8.
小结:运用幂的运算公式,可将问题化繁为简,
负数乘方结果的符号,奇次方得负,偶次方得正.
四、典型例题
归纳总结:幂的运算性质包括同底数幂的乘法、幂的乘方、积的乘方及
同底数幂的除法.这四种运算性质贯穿全章,是整式乘除及因式分解的
基础.其逆向运用可以使一些计算简便,从而培养一定的计算技巧,达
到学以致用的目的.
【当堂检测】
2.(1)若∣p+3∣=(-2019)0,则p= ;
(2)若(x-2)0=1,则x应满足的条件是 .
1.下列计算不正确的是( )
A.2a3 ÷a=2a2 B. (-a3)2=a6
C. a4 ·a3=a7 D. a2·a4=a8
-4或-2
x≠2
D
解析:a2·a4=a2+4=a6,故D选项错误.
解析:任何不等于0的数的0次幂都等于1,;故(1)中∣p+3∣=1,(2)中x-2≠0.
【当堂检测】
3. (1)计算:0.252019 ×(-4)2019-8100 ×0.5301;
(2)比较大小:420与1510.
解:(1)原式=[0.25 ×(-4)]2019-(23)100 ×0.5300 ×0.5
(2) ∵420=(42)10=1610,1610>1510, ∴420>1510.
=-1-(2 ×0.5)300 ×0.5
=-1-0.5
=-1.5;
【当堂检测】
4.已知10x=5,10y=6,求103x+2y的值.
103x+2y
=103x 102y
=(10x)3 (10y)2
=53×62
=4500.
解:
四、典型例题
例3.计算:[x(x2y2-xy)-y(x2-x3y)] ÷3x2y,其中x=1,y=3.
分析:在计算整式的加、减、乘、除、乘方的运算中,一要注意运算顺序;
二要熟练正确地运用运算法则.
解:原式=(x3y2-x2y-x2y+x3y2)÷3x2y
当x=1,y=3时,原式= .
=(2x3y2-2x2y) ÷3x2y
= - .
(二)整式的运算
四、典型例题
归纳总结:整式的乘除法主要包括单项式乘以单项式、单项式乘以多项式、
多项式乘以多项式以及单项式除以单项式、多项式除以单项式,其中单项式
乘以单项式是整式乘除的基础,必须熟练掌握它们的运算法则,整式的混合
运算,要按照先算乘方,再算乘除,最后算加减的顺序进行,有括号的要算
括号里的.
【当堂检测】
5.计算:(1)(2a+5b)(a-3b);(2)(x+1)(x2-x+1);
(3)(3x-2y)(y-3x)-(2x-y)(3x+y).
解:(1)原式=2a2-6ab+5ab-15b2
=2a2-ab-15b2.
(2)原式=x3-x2+x+x2-x+1
=x3+1.
(3)原式=(-9x2+9xy-2y2)-(6x2-xy-y2)
=-15x2+10xy-y2.
【当堂检测】
6.(1)一个长方形的面积是a2-2ab+a,宽为a,则长方形的长为 ;
(2)已知多项式2x3-4x2-1除以一个多项式A,得商为2x,余式为x-1,
则这个多项式A是 .
a-2b+1
x2-2x-
四、典型例题
(三)整式的乘法公式的运用
例4.先化简再求值:[(x-y)2+(x+y)(x-y)] ÷2x,其中x=3,y=1.5.
分析:运用平方差公式和完全平方公式,先计算括号内的,再计算整式 的除法运算.
解:原式=(x2-2xy+y2+x2-y2) ÷2x
=(2x2-2xy) ÷2x
=x-y.
当x=3,y=1.5时,原式=3-1.5=1.5.
四、典型例题
归纳总结:整式的乘法公式包括平方差公式和完全平方公式,而完全平方
公式又分为两个:两数和的完全平方公式和两数差的完全平方公式,在计
算多项式的乘法时,对于符合这三个公式结构特征的式子,运用公式可减
少运算量,提高解题速度.
【当堂检测】
8.(1)求方程(x-1)2-(x-1)(x+1)+3(1-x)=0的解;
(2)已知x2+9y2+4x-6y+5=0,求xy的值.
解:(1)原方程可化为-5x+5=0,解得x=1.
(2) ∵x2+9y2+4x-6y+5=0,
∴(x2+4x+4)+(9y2-6y+1)=0,
∴(x+2)2+(3y-1)2=0.
∴x+2=0,3y-1=0,解得x=-2, y= ,
【当堂检测】
9.计算:[(x+2y)2-(x+y)(3x-y)-5y2]÷2x.
解:原式=(x2+4xy+4y2-3x2+xy-3xy+y2-5y2)÷2x
=(-2x2+2xy)÷2x
=-x+y.
四、典型例题
(四)实际问题转化为数学模型
解析:图(1)的阴影 部分面积是两个正方形的面积差(a2-b2),图(2)梯形的
面积是(2a+2b)(a-b)÷2=(a+b)(a-b),根据面积相等,得a2-b2=(a+b)(a-b).
例6.如图所示,在边长为a的正方形中剪去边长为b的小正方形,把剩下的部分
拼成梯形,分别计算这两个图形的阴影部分的面积,验证公式是 .
a2-b2=(a+b)(a-b)
b
a
a
a
a
b
b
b
b
a-b
b
(2)
(1)
归纳总结:本章中数形结合思想主要体现在根据给定的图形写出一个代数恒等式或根据代数式画出几何图形. 由几何图形得到代数恒等式时,需要用不同的方法表示几何图形的面积,然后得出代数恒等式;由代数恒等式画图时,关键在于合理拼接,往往是相等的边拼到一起.
四、典型例题
【当堂检测】
10. 我们已知道,完全平方公式可以用平面几何图形的面积来表示,
实际上还有一个代数恒等式也可以用这种形式来表示,例如
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①和图②等图形的面积表示.
a
a
a
b
b
ab
ab
ab
a2
a2
b2
图①
b2
a2
a2
ab
ab
ab
a
a
a
b
b
图②
(2)请画一个几何图形,使它的面积能表示(a+b)(a+3b)=a2+4ab+3b2.
(1)请写出图③所表示的代数恒等式;
b
b
a
a
b
a
ab
ab
ab
ab
ab
a2
a2
b2
b2
图③
解:(2a+b)(a+2b)=2a2+5ab+2b2;
如图④.
图④
a2
b
a
ab
ab
ab
ab
b2
b2
b2
a
b
b
b
【当堂检测】
五、课堂总结
幂的运算
乘法公式
整式的乘除
积的乘方
平方差公式
多项式与单项式相乘、相除
完全平方公式
整式的乘除法
单项式与单项式相乘、相除
多项式与多项式相乘
同底数幂相乘
幂的乘方
同底数幂相除
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
