9.4平行线的判定同步练习青岛版(2012)数学七年级下册(含答案)
文档属性
| 名称 | 9.4平行线的判定同步练习青岛版(2012)数学七年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 391.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 19:52:05 | ||
图片预览


文档简介
9.4平行线的判定同步练习青岛版(2012)数学七年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在同一平面内,经过直线外一点的4条直线中,与相交的直线至少有( )
A.4条 B.3条 C.2条 D.1条
2.在同一平面内,下列说法:①过两点有且只有一条直线;②两条不相同的直线有且只有一个公共点;③经过直线外一点有且只有一条直线与已知直线垂直;④经过直线外一点有且只有一条直线与已知直线平行,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.如图,在四边形中,点在上,连接,下列说法正确的是( ).
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
4.下列说法中正确的有( )
①内错角相等 ②平行于同一条直线的两条直线平行
③相等的角是对顶角 ④经过直线外一点,有且只有一条直线与已知直线平行
A.①② B.①③ C.②④ D.③④
5.下列说法错误的是( )
A.在同一平面内,直线a∥b,若c与a相交,则b与c也相交
B.在同一平面内,直线a与b相交,c与a相交,则b∥c
C.在同一平面内,两条不平行的直线是相交线
D.直线AB与CD平行,则AB上所有点都在CD的同侧
6.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
7.如图,由已知条件推出结论正确的是( )
A.由,可以推出 B.由,可以推出
C.由,可以推出 D.由,可以推出
8.同一平面内,经过直线外一点画直线,下列说法错误的是( )
A.可以画无数条直线与这条直线相交
B.可以画无数条直线与这条直线平行
C.能且只能画一条直线与这条直线平行
D.能且只能画一条直线与这条直线垂直
9.下列说法正确的个数是( )
经过一点有且只有一条直线与已知直线平行:
垂直于同一条直线的两条直线互相平行;
直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
同一平面内不相交的两条直线叫做平行线.
A.1个 B.2个 C.3个 D.4个
10.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=69°,若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
A.69° B.49° C.31° D.21°
二、填空题
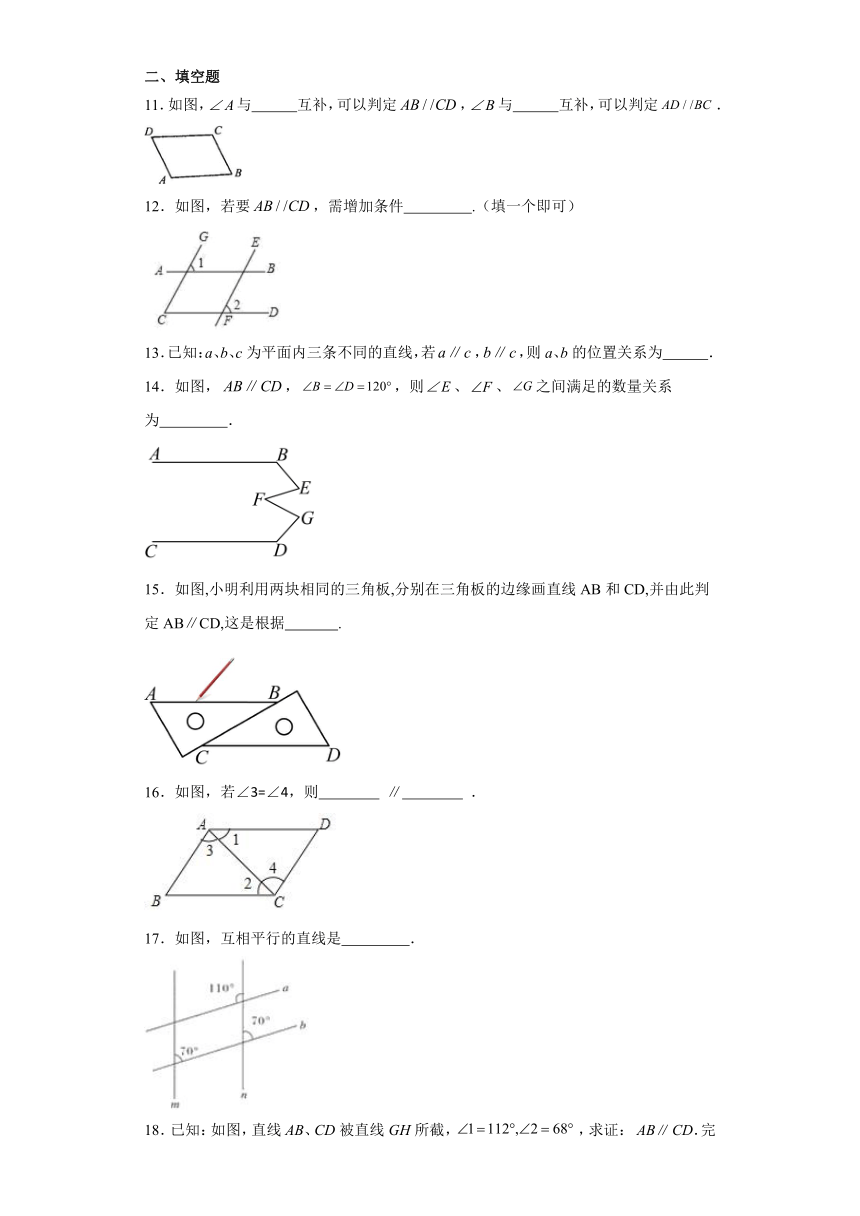
11.如图,与 互补,可以判定,与 互补,可以判定.
12.如图,若要,需增加条件 .(填一个即可)
13.已知:a、b、c为平面内三条不同的直线,若,,则a、b的位置关系为 .
14.如图,,,则、、之间满足的数量关系为 .
15.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线AB和CD,并由此判定AB∥CD,这是根据 .
16.如图,若∠3=∠4,则 ∥ .
17.如图,互相平行的直线是 .
18.已知:如图,直线AB、CD被直线GH所截,,求证: ABCD.完成下面的证明:
证明:∵AB被直线GH所截,
∴
∵
∴
∴ ( )(填推理的依据).
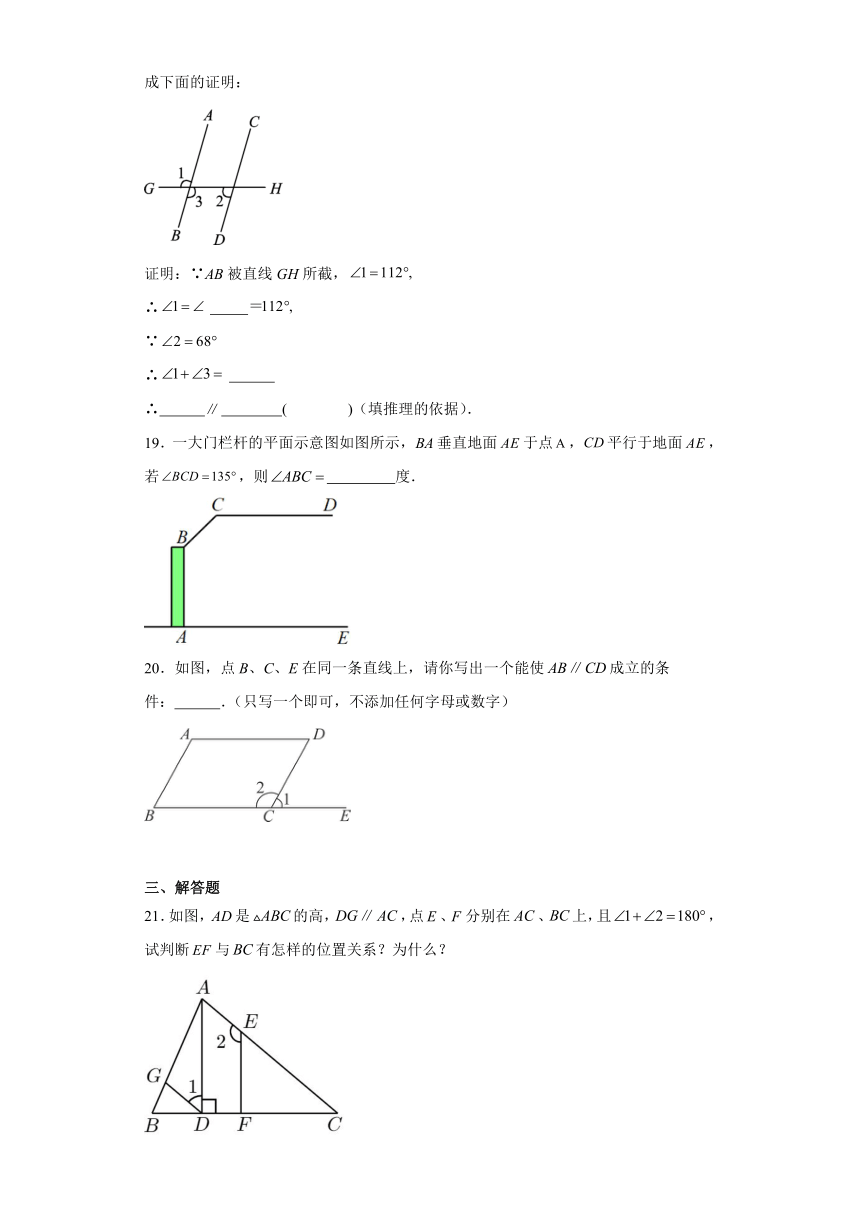
19.一大门栏杆的平面示意图如图所示,垂直地面于点,平行于地面,若,则 度.
20.如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件: .(只写一个即可,不添加任何字母或数字)
三、解答题
21.如图,是的高,,点、分别在、上,且,试判断与有怎样的位置关系?为什么?
22.已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠KOH的度数是多少?
23.如图,推理填空:
(1)∵∠A =∠_____(已知),
∴AC∥ED( );
(2)∵∠2 =∠_____(已知),
∴AC∥ED( );
(3)∵∠A +∠____= 180°(已知),
∴AB∥FD( );
(4)∵AC∥ED(已知),
∴∠2 +∠____ = 180°( );
24.综合与实践
数学社团的同学以“两条平行线,和一块含角的直角三角尺”为主题开展数学活动,已知点E,F不可能同时落在直线和之间.
探究:(1)如图1,把三角尺的角的顶点E,G分别放在,上,若,求的度数;
类比:(2)如图2,把三角尺的锐角顶点G放在上,且保持不动,若点E恰好落在和之间,且与所夹锐角为,求的度数;
迁移:(3)把三角尺的锐角顶点G放在上,且保持不动,旋转三角尺,若存在,直接写出射线与所夹锐角的度数.
25.在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系.(其中)
(1)将三角尺如图1所示叠放在一起(直角顶点重合),
当时,__________;
(2)小亮固定其中一块三角尺不变,绕点顺时针转动另一块三角尺,从图2的与重合开始,到图3的与在一条直线上时结束.
探索的一边与的一边平行的情况.
①求当时,如图4所示,的大小;
②当的一边与的一边平行时,请直接写出的其余所有可能值.
参考答案:
1.B
2.C
3.C
4.C
5.B
6.A
7.B
8.B
9.A
10.D
11.
12.
13.
14.
15.内错角相等,两直线平行
16. AB CD
17.m∥n,a∥b.
18. 3 180° AB CD 同旁内角互补,两直线平行
19.
20.或或
21.,
22.(1)AB∥CD;(2)40°.
23.(1)BED;
(2)同位角相等,两直线平行;
(3)DFC;
(4)内错角相等,两直线平行;
(5)DFA;
(6)同旁内角互补,两直线平行;
(7)AFD;
(8)同旁内角互补,两直线平行;
24.(1)
(2)
(3)或
25.(1)30
(2)①;②或或或
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在同一平面内,经过直线外一点的4条直线中,与相交的直线至少有( )
A.4条 B.3条 C.2条 D.1条
2.在同一平面内,下列说法:①过两点有且只有一条直线;②两条不相同的直线有且只有一个公共点;③经过直线外一点有且只有一条直线与已知直线垂直;④经过直线外一点有且只有一条直线与已知直线平行,其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
3.如图,在四边形中,点在上,连接,下列说法正确的是( ).
A.因为,所以
B.因为,所以
C.因为,所以
D.因为,所以
4.下列说法中正确的有( )
①内错角相等 ②平行于同一条直线的两条直线平行
③相等的角是对顶角 ④经过直线外一点,有且只有一条直线与已知直线平行
A.①② B.①③ C.②④ D.③④
5.下列说法错误的是( )
A.在同一平面内,直线a∥b,若c与a相交,则b与c也相交
B.在同一平面内,直线a与b相交,c与a相交,则b∥c
C.在同一平面内,两条不平行的直线是相交线
D.直线AB与CD平行,则AB上所有点都在CD的同侧
6.已知直线a∥b,将一块含30°角的直角三角板(∠BAC=30°)按如图所示方式放置,并且顶点A,C分别落在直线a,b上,若∠1=22°,则∠2的度数是( )
A.38° B.45° C.58° D.60°
7.如图,由已知条件推出结论正确的是( )
A.由,可以推出 B.由,可以推出
C.由,可以推出 D.由,可以推出
8.同一平面内,经过直线外一点画直线,下列说法错误的是( )
A.可以画无数条直线与这条直线相交
B.可以画无数条直线与这条直线平行
C.能且只能画一条直线与这条直线平行
D.能且只能画一条直线与这条直线垂直
9.下列说法正确的个数是( )
经过一点有且只有一条直线与已知直线平行:
垂直于同一条直线的两条直线互相平行;
直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
同一平面内不相交的两条直线叫做平行线.
A.1个 B.2个 C.3个 D.4个
10.如图,直线a与直线b被直线c所截,b⊥c,垂足为A,∠1=69°,若使直线b与直线a平行,则可将直线b绕着点A顺时针旋转( )
A.69° B.49° C.31° D.21°
二、填空题
11.如图,与 互补,可以判定,与 互补,可以判定.
12.如图,若要,需增加条件 .(填一个即可)
13.已知:a、b、c为平面内三条不同的直线,若,,则a、b的位置关系为 .
14.如图,,,则、、之间满足的数量关系为 .
15.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线AB和CD,并由此判定AB∥CD,这是根据 .
16.如图,若∠3=∠4,则 ∥ .
17.如图,互相平行的直线是 .
18.已知:如图,直线AB、CD被直线GH所截,,求证: ABCD.完成下面的证明:
证明:∵AB被直线GH所截,
∴
∵
∴
∴ ( )(填推理的依据).
19.一大门栏杆的平面示意图如图所示,垂直地面于点,平行于地面,若,则 度.
20.如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件: .(只写一个即可,不添加任何字母或数字)
三、解答题
21.如图,是的高,,点、分别在、上,且,试判断与有怎样的位置关系?为什么?
22.已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠KOH的度数是多少?
23.如图,推理填空:
(1)∵∠A =∠_____(已知),
∴AC∥ED( );
(2)∵∠2 =∠_____(已知),
∴AC∥ED( );
(3)∵∠A +∠____= 180°(已知),
∴AB∥FD( );
(4)∵AC∥ED(已知),
∴∠2 +∠____ = 180°( );
24.综合与实践
数学社团的同学以“两条平行线,和一块含角的直角三角尺”为主题开展数学活动,已知点E,F不可能同时落在直线和之间.
探究:(1)如图1,把三角尺的角的顶点E,G分别放在,上,若,求的度数;
类比:(2)如图2,把三角尺的锐角顶点G放在上,且保持不动,若点E恰好落在和之间,且与所夹锐角为,求的度数;
迁移:(3)把三角尺的锐角顶点G放在上,且保持不动,旋转三角尺,若存在,直接写出射线与所夹锐角的度数.
25.在数学实践活动课上,小亮同学利用一副三角尺探索与研究共直角顶点的两个直角三角形中的位置关系与数量关系.(其中)
(1)将三角尺如图1所示叠放在一起(直角顶点重合),
当时,__________;
(2)小亮固定其中一块三角尺不变,绕点顺时针转动另一块三角尺,从图2的与重合开始,到图3的与在一条直线上时结束.
探索的一边与的一边平行的情况.
①求当时,如图4所示,的大小;
②当的一边与的一边平行时,请直接写出的其余所有可能值.
参考答案:
1.B
2.C
3.C
4.C
5.B
6.A
7.B
8.B
9.A
10.D
11.
12.
13.
14.
15.内错角相等,两直线平行
16. AB CD
17.m∥n,a∥b.
18. 3 180° AB CD 同旁内角互补,两直线平行
19.
20.或或
21.,
22.(1)AB∥CD;(2)40°.
23.(1)BED;
(2)同位角相等,两直线平行;
(3)DFC;
(4)内错角相等,两直线平行;
(5)DFA;
(6)同旁内角互补,两直线平行;
(7)AFD;
(8)同旁内角互补,两直线平行;
24.(1)
(2)
(3)或
25.(1)30
(2)①;②或或或
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
