人教版五年级下册第2 单元《质数与合数》说课稿
文档属性
| 名称 | 人教版五年级下册第2 单元《质数与合数》说课稿 |  | |
| 格式 | docx | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 19:54:02 | ||
图片预览

文档简介
质数与合数 说课稿
学科:数学 教材版本:人教版五年级上册
尊敬的各位评委老师,大家好!
我要与大家分享的说课题目是:人教版五年级下册第二单元《质数与合数》。
本单元分为以下的三大部分:质数与合数的本质意义是本单元学习的基础,奇数偶数的概念由倍数的概念引发,质数合数的概念,由因数的概念引发。在解决问题的过程中,概念的联系十分紧密,互为工具和资源,所以在教学设计的过程中,我把握一个中心整体教学,也就是尽量为学生创设解决问题,推导新知的机会,帮助他们串联所学概念,从而达到通过应用,巩固理解,依靠理解,促进记忆。基于为学生创设可探究有趣味的活动情境的想法,我把三个数学魔术融入了本单元的教学。今天我和大家分享的就是第二个数学魔术在教学中的应用。
启动课堂的环节是一个数学魔术,魔术,总是需要与观众互动的,所以我会先用一种比较特别的方式,挑选一个可爱的小助手。课前给每个学生发放一封具数学味道的信件,请他们在1-20之间任选一个他非常喜欢的数字在信封(内有不同花色2-13的扑克牌)上写下来。
我会和他们说:老师的小助手,就是你们之中所选的数字,因数的个数最少的小朋友,你选的数字将会决定你是不是幸运的小助手,这是我为学生创设的一个有意义的学习情境,他使学生主动去做寻找因数的动作,谁的数字因数多,谁的数字因数少,孩子们会关注到,每个数字的因数个数大有区别,也为我后面推出核心知识做一个铺垫。
接下来我来演示一下摸牌术,我会先请小助手帮我检查一下这副混乱的扑克牌,在把扑克牌收起来的时候,随机的把它分成两堆,请我的小助手任选其中的一堆,并将它充分的洗乱,然后在这堆洗乱的牌中间任选一张,拿给大家看,请大家记住它的花色和点数,但是我会跟小助手说,不要让老师看到,然后这张扑克牌再插入另一堆的扑克牌堆中,把这堆牌也交给他,随意的洗乱,所以现在在这里有一张扑克牌,你们都知道它的花色和点数,唯独我不知道,但是不要紧,我只要施展数学老师的感应能力,就能够摸出你们所看到的这张扑克牌。好,我找到了,请大家大声的说出你们所看到的这一张扑克牌的花色和点数是否与我手中的扑克牌一样?
演示完魔术以后,抓住学生强烈的好奇心,我会启动一个问题,52张不一样的扑克牌分成两堆,我如何能从其中的一堆辨识出另一堆的内脏?这个关键问题是学习真正的起点,它使学习者从观赏魔术的心情自然的切换到数学的思考和探究,带出了魔术背后分类的内涵,到底是按什么标准来分类的?
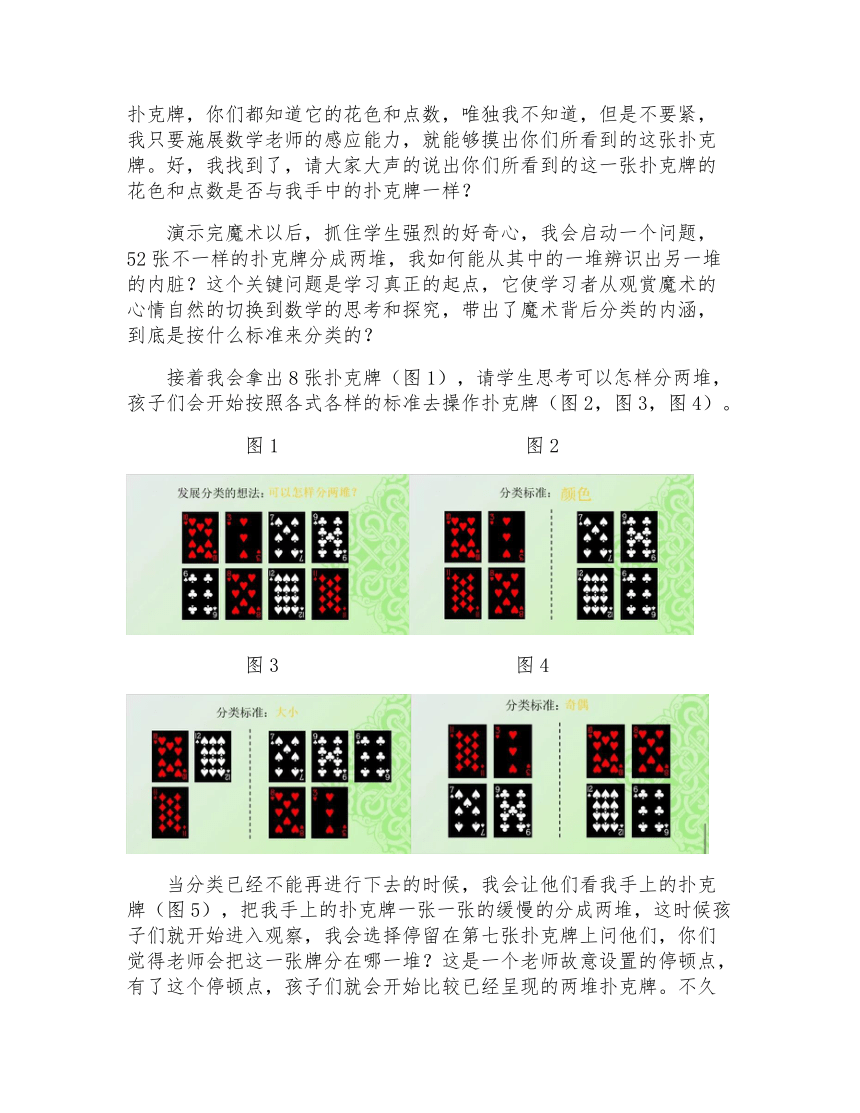
接着我会拿出8张扑克牌(图1),请学生思考可以怎样分两堆,孩子们会开始按照各式各样的标准去操作扑克牌(图2,图3,图4)。
图1 图2
图3 图4
当分类已经不能再进行下去的时候,我会让他们看我手上的扑克牌(图5),把我手上的扑克牌一张一张的缓慢的分成两堆,这时候孩子们就开始进入观察,我会选择停留在第七张扑克牌上问他们,你们觉得老师会把这一张牌分在哪一堆?这是一个老师故意设置的停顿点,有了这个停顿点,孩子们就会开始比较已经呈现的两堆扑克牌。不久之后他们会奇怪的发现,我竟然把2分在了左边的这一堆,再以同样的方法处理9的问题,增加学生的困惑。
图5 图6
这两堆扑克牌到底各有什么共性?我会先让学生说一下。我的经验是孩子们通常会先忽略2和9做出奇偶分类的判断,但是很快他们自己会意识到不对,奇中有偶,偶中有奇,打破了这样的一种猜想,那数字之间到底还可能因为什么而有所不同?如果用因数,倍数的眼光来看待这些数字,你又发现了什么?
这时候课堂开头看似随意的小游戏,就有可能成为学生头脑中的资源,提供给他们新的想法。
我会请他们在信封中的扑克牌上写出这些数字的因数,当他们发现因数的个数就是分类的标准的时候,就推出质数与合数的概念,让他们一目了然(图6)。
所以在这里有一副张张不同的扑克牌,但在一个数学老师的眼里只有两种面貌,一种叫做质数(图7),另一种叫做合数(图8)。
图7 图8
老师所使用的扑克牌及你们信封中的扑克牌都是一部没有1的扑克牌,为什么把1拿出了呢?因为1只有一个因数1,所以1既不是质数,也不是合数(图9)。 图9
在这个时候做这样的一个小结有什么意义呢?是数学让混乱的表象变得简约,而孩子们也会瞬间感觉到扑克牌的优雅,因为在扑克牌中,质数和合数是一样多的,而1刚好被独立了出来。至此魔术解密,而孩子们也在不知不觉中收获了新知。
接下来我会请他们试试身手,问他们17是不是一个质数,21是不是一个质数?我会强调,当我在问这个问题的时候,其实我是在问什么?我是在问17是不是只有1和17这两个因数?21是不是只有1和21这两个因数?
有时候孩子们知道了概念是什么,但在解决问题的时候,他并不知道,如何使我的操作和概念对应起来,所以我觉得做这样的强调非常的有必要,孩子们可能会开始一个的去做检测,或者去做寻找第三个因素的动作,那老师可以带着他们归纳出,判断一个数是否质数的方法,可以正向检测,也可以逆向排除。
等他们有了一定的经验以后,我会尝试让他们处理百数表,给他们每人一张这样百数表,请他们在小组内共同完成一些任务。首先是快速的筛选一次质数,只要你觉得这个数字长得像质数,就把它圈出。第二步就要深入思考了,你可以对于你认为不是质数的某个数,找出第三个因数,你必须要有充分的理由,第三步就是归纳整理、交流和分享。
孩子天生有在游戏中学习的本领,这个活动,其实提供给他们一个相互切磋的机会,在操作的过程中所产生的对话可能是相互提醒,相互质疑,相互补充,而小伙伴之间共学,互学的效率,有时候和老师直接讲大有不同。
在交流和分享的阶段,他们也会因为手上有这样的一个画面,这样的一份资源,更有可能发现偶数中只有2是质数,整十整百数都是合数,这样的一些结论。
之后我会请他们用自己喜欢的方式制作一张质数。本课会结束,在同学们相互欣赏对方作品的友好氛围中。
我留给他们的课堂作业有两个:一.表演摸牌术,二.读懂神秘表格。我会和他们说,这其实不是一个普通的表格,它其实是一份很适合在某些特定的节日送出的礼物,只要你把里面的字数找出来,用红色涂掉,你就知道他到底想表达一些什么了。比如说在父亲节,母亲节或教师节,考考你的爸爸妈妈或老师,并且告诉他们有了数学你才能读懂我的心(图10)。 图10
情境我以破解摸排数为主线,引发了孩子们进一步了解整数的分类的需求,引出了质数合数的概念,帮助孩子建立了质数合数的分类标准,来源于因数的组成结构的认识。
通过学习,孩子们掌握了判断一个数是否质数的基础方法,同时感受到了分类在生活中的应用,感受到了数学的好玩有趣。
在达成这一系列教学目标的过程中,课堂不只是指向单一的知识点,而是再现了知识之间的逻辑联系。在这节课上,孩子们经历了观察、猜测、验证、归纳等种种数学体验,提升了应用数学知识,解决问题的信心和能力。另外当孩子们发现生活中随处可见的扑克牌,竟然也可以是数学课的素材,是数学的力量,使平凡的事物展现出了不平凡的魅力。他们就会慢慢转变看待数学,看待学习的眼光。
学科:数学 教材版本:人教版五年级上册
尊敬的各位评委老师,大家好!
我要与大家分享的说课题目是:人教版五年级下册第二单元《质数与合数》。
本单元分为以下的三大部分:质数与合数的本质意义是本单元学习的基础,奇数偶数的概念由倍数的概念引发,质数合数的概念,由因数的概念引发。在解决问题的过程中,概念的联系十分紧密,互为工具和资源,所以在教学设计的过程中,我把握一个中心整体教学,也就是尽量为学生创设解决问题,推导新知的机会,帮助他们串联所学概念,从而达到通过应用,巩固理解,依靠理解,促进记忆。基于为学生创设可探究有趣味的活动情境的想法,我把三个数学魔术融入了本单元的教学。今天我和大家分享的就是第二个数学魔术在教学中的应用。
启动课堂的环节是一个数学魔术,魔术,总是需要与观众互动的,所以我会先用一种比较特别的方式,挑选一个可爱的小助手。课前给每个学生发放一封具数学味道的信件,请他们在1-20之间任选一个他非常喜欢的数字在信封(内有不同花色2-13的扑克牌)上写下来。
我会和他们说:老师的小助手,就是你们之中所选的数字,因数的个数最少的小朋友,你选的数字将会决定你是不是幸运的小助手,这是我为学生创设的一个有意义的学习情境,他使学生主动去做寻找因数的动作,谁的数字因数多,谁的数字因数少,孩子们会关注到,每个数字的因数个数大有区别,也为我后面推出核心知识做一个铺垫。
接下来我来演示一下摸牌术,我会先请小助手帮我检查一下这副混乱的扑克牌,在把扑克牌收起来的时候,随机的把它分成两堆,请我的小助手任选其中的一堆,并将它充分的洗乱,然后在这堆洗乱的牌中间任选一张,拿给大家看,请大家记住它的花色和点数,但是我会跟小助手说,不要让老师看到,然后这张扑克牌再插入另一堆的扑克牌堆中,把这堆牌也交给他,随意的洗乱,所以现在在这里有一张扑克牌,你们都知道它的花色和点数,唯独我不知道,但是不要紧,我只要施展数学老师的感应能力,就能够摸出你们所看到的这张扑克牌。好,我找到了,请大家大声的说出你们所看到的这一张扑克牌的花色和点数是否与我手中的扑克牌一样?
演示完魔术以后,抓住学生强烈的好奇心,我会启动一个问题,52张不一样的扑克牌分成两堆,我如何能从其中的一堆辨识出另一堆的内脏?这个关键问题是学习真正的起点,它使学习者从观赏魔术的心情自然的切换到数学的思考和探究,带出了魔术背后分类的内涵,到底是按什么标准来分类的?
接着我会拿出8张扑克牌(图1),请学生思考可以怎样分两堆,孩子们会开始按照各式各样的标准去操作扑克牌(图2,图3,图4)。
图1 图2
图3 图4
当分类已经不能再进行下去的时候,我会让他们看我手上的扑克牌(图5),把我手上的扑克牌一张一张的缓慢的分成两堆,这时候孩子们就开始进入观察,我会选择停留在第七张扑克牌上问他们,你们觉得老师会把这一张牌分在哪一堆?这是一个老师故意设置的停顿点,有了这个停顿点,孩子们就会开始比较已经呈现的两堆扑克牌。不久之后他们会奇怪的发现,我竟然把2分在了左边的这一堆,再以同样的方法处理9的问题,增加学生的困惑。
图5 图6
这两堆扑克牌到底各有什么共性?我会先让学生说一下。我的经验是孩子们通常会先忽略2和9做出奇偶分类的判断,但是很快他们自己会意识到不对,奇中有偶,偶中有奇,打破了这样的一种猜想,那数字之间到底还可能因为什么而有所不同?如果用因数,倍数的眼光来看待这些数字,你又发现了什么?
这时候课堂开头看似随意的小游戏,就有可能成为学生头脑中的资源,提供给他们新的想法。
我会请他们在信封中的扑克牌上写出这些数字的因数,当他们发现因数的个数就是分类的标准的时候,就推出质数与合数的概念,让他们一目了然(图6)。
所以在这里有一副张张不同的扑克牌,但在一个数学老师的眼里只有两种面貌,一种叫做质数(图7),另一种叫做合数(图8)。
图7 图8
老师所使用的扑克牌及你们信封中的扑克牌都是一部没有1的扑克牌,为什么把1拿出了呢?因为1只有一个因数1,所以1既不是质数,也不是合数(图9)。 图9
在这个时候做这样的一个小结有什么意义呢?是数学让混乱的表象变得简约,而孩子们也会瞬间感觉到扑克牌的优雅,因为在扑克牌中,质数和合数是一样多的,而1刚好被独立了出来。至此魔术解密,而孩子们也在不知不觉中收获了新知。
接下来我会请他们试试身手,问他们17是不是一个质数,21是不是一个质数?我会强调,当我在问这个问题的时候,其实我是在问什么?我是在问17是不是只有1和17这两个因数?21是不是只有1和21这两个因数?
有时候孩子们知道了概念是什么,但在解决问题的时候,他并不知道,如何使我的操作和概念对应起来,所以我觉得做这样的强调非常的有必要,孩子们可能会开始一个的去做检测,或者去做寻找第三个因素的动作,那老师可以带着他们归纳出,判断一个数是否质数的方法,可以正向检测,也可以逆向排除。
等他们有了一定的经验以后,我会尝试让他们处理百数表,给他们每人一张这样百数表,请他们在小组内共同完成一些任务。首先是快速的筛选一次质数,只要你觉得这个数字长得像质数,就把它圈出。第二步就要深入思考了,你可以对于你认为不是质数的某个数,找出第三个因数,你必须要有充分的理由,第三步就是归纳整理、交流和分享。
孩子天生有在游戏中学习的本领,这个活动,其实提供给他们一个相互切磋的机会,在操作的过程中所产生的对话可能是相互提醒,相互质疑,相互补充,而小伙伴之间共学,互学的效率,有时候和老师直接讲大有不同。
在交流和分享的阶段,他们也会因为手上有这样的一个画面,这样的一份资源,更有可能发现偶数中只有2是质数,整十整百数都是合数,这样的一些结论。
之后我会请他们用自己喜欢的方式制作一张质数。本课会结束,在同学们相互欣赏对方作品的友好氛围中。
我留给他们的课堂作业有两个:一.表演摸牌术,二.读懂神秘表格。我会和他们说,这其实不是一个普通的表格,它其实是一份很适合在某些特定的节日送出的礼物,只要你把里面的字数找出来,用红色涂掉,你就知道他到底想表达一些什么了。比如说在父亲节,母亲节或教师节,考考你的爸爸妈妈或老师,并且告诉他们有了数学你才能读懂我的心(图10)。 图10
情境我以破解摸排数为主线,引发了孩子们进一步了解整数的分类的需求,引出了质数合数的概念,帮助孩子建立了质数合数的分类标准,来源于因数的组成结构的认识。
通过学习,孩子们掌握了判断一个数是否质数的基础方法,同时感受到了分类在生活中的应用,感受到了数学的好玩有趣。
在达成这一系列教学目标的过程中,课堂不只是指向单一的知识点,而是再现了知识之间的逻辑联系。在这节课上,孩子们经历了观察、猜测、验证、归纳等种种数学体验,提升了应用数学知识,解决问题的信心和能力。另外当孩子们发现生活中随处可见的扑克牌,竟然也可以是数学课的素材,是数学的力量,使平凡的事物展现出了不平凡的魅力。他们就会慢慢转变看待数学,看待学习的眼光。
