青岛版八年级上册第2章2.5角平分线的性质同步训练题(含答案)
文档属性
| 名称 | 青岛版八年级上册第2章2.5角平分线的性质同步训练题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 118.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-19 00:00:00 | ||
图片预览

文档简介
青岛版八年级上册第2章2.5角平分线的性质同步训练题(含答案)
一.选择题(共10小题)
1.(2015 茂名)如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B. 5 C. 4 D. 3
(1题图) (2题图) (3题图)
2.(2015 青岛)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B. 2 C. 3 D. +2
3.(2015 湖州)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B. 7 C. 5 D. 4
4.(2015 丹东模拟)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为( )
A. B. 2 C. 3 D. 2
(4题图) (5题图) (6题图)
5.(2015 高新区校级模拟)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B. 12 C. 4 D. 6
6.(2015 从化市一模)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
A.7 B. 6 C. 5 D. 4
7.(2015 河北模拟)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B. 8 C. 15 D. 无法确定
8.(2015 威海模拟)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
A. B. 2 C. D.
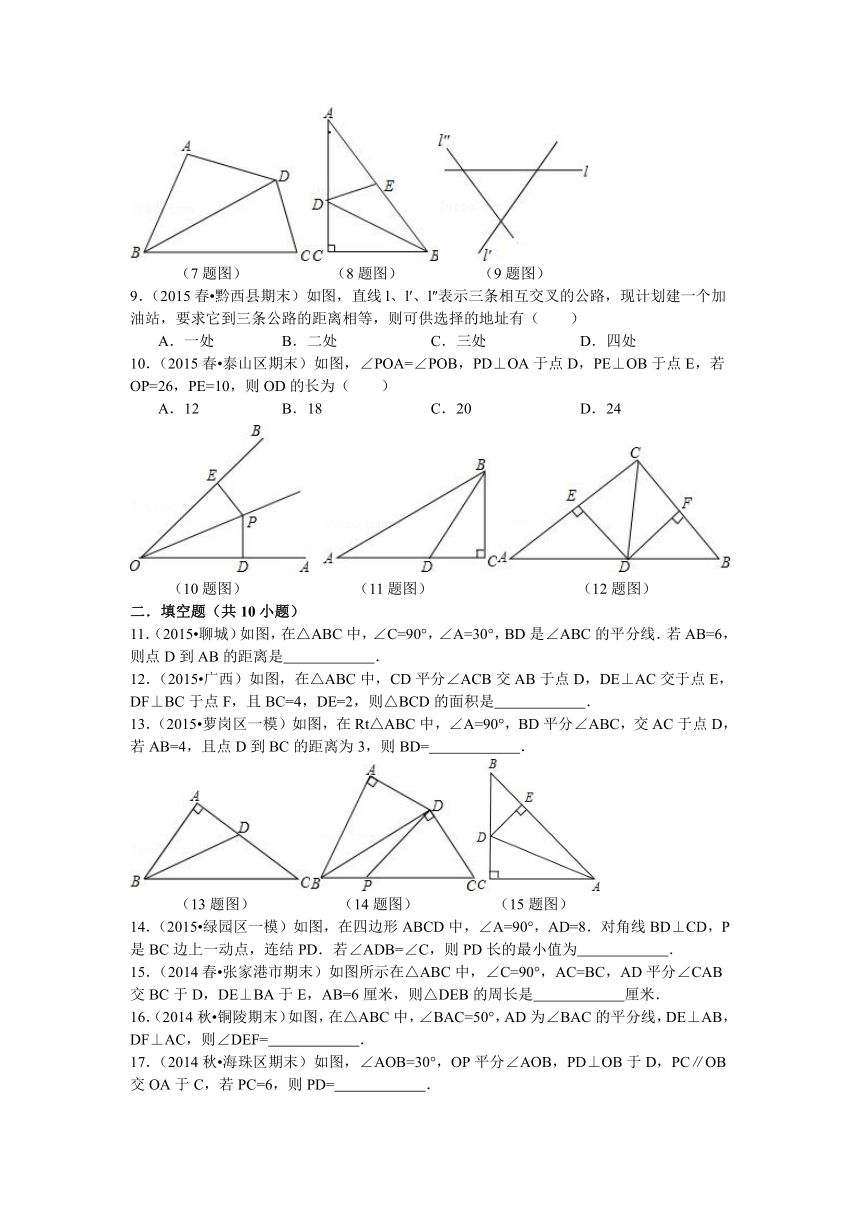
(7题图) (8题图) (9题图)
9.(2015春 黔西县期末)如图,直线l、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B. 二处 C. 三处 D. 四处
10.(2015春 泰山区期末)如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
A.12 B. 18 C. 20 D. 24
(10题图) (11题图) (12题图)
二.填空题(共10小题)
11.(2015 聊城)如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是 .
12.(2015 广西)如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
13.(2015 萝岗区一模)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD= .
(13题图) (14题图) (15题图)
14.(2015 绿园区一模)如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为 .
15.(2014春 张家港市期末)如图所示在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥BA于E,AB=6厘米,则△DEB的周长是 厘米.
16.(2014秋 铜陵期末)如图,在△ABC中,∠BAC=50°,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,则∠DEF= .
17.(2014秋 海珠区期末)如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= .
(16题图) (17题图) (18题图)
18.(2015 徐州)如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A= °.
19.(2015春 邳州市期末)如图,在△ABC中,AB=AC,∠A=20°,边AC的垂直平分线交AC于点D,交AB于点E,则∠BCE等于 °.
(19题图) (20题图)
20.(2015 忻州校级模拟)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=2,BC=9,则△BDC的面积是 .
三.解答题(共4小题)
21.(2015春 泰山区期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.
22.(2015春 福鼎市校级月考)如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
23.(2014秋 日照期末)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=16cm,AC=12cm,求DE的长.
24.(2014秋 莘县期末)如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF.
青岛版八年级上册第2章2.5角平分线的性质同步训练题参考答案
一.选择题(共10小题)
1.A 2.C 3.C 4.C 5.D 6.D 7.A 8.A 9.D 10.D
二.填空题(共10小题)
11. 12.4 13.5 14.8 15.6 16.25° 17.3
18.87 19.60 20.9
三.解答题(共4小题)
21.(1)证明:∵在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,
∴CD=DE,∠AED=∠C=90°,∠CAD=∠EAD,
在△ACD和△AED中∴△ACD≌△AED,∴AC=AE;
(2)解:∵DE⊥AB,点E为AB的中点,∴AD=BD,
∴∠B=∠DAB=∠CAD,
∵∠C=90°,
∴3∠B=90°,
∴∠B=30°,
∵CD=DE=4,∠DEB=90°,
∴BD=2DE=8,
由勾股定理得:BE==4.
22.解:(1)∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,
∴∠PCD=∠PDC;
(2)OP是CD的垂直平分线.
理由:∵∠OCP=∠ODP=90°,
在Rt△POC和Rt△POD中,
,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD,
由PC=PD,OC=OD,可知点O、P都是线段CD的垂直平分线上的点,
从而OP是线段CD的垂直平分线.
23.∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵S△ABC=S△ABD+S△ACD=AB×DE+AC×DF
∴S△ABC=(AB+AC)×DE
即×(16+12)×DE=28,
故DE=2(cm).
24.证明:∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD.
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF.
一.选择题(共10小题)
1.(2015 茂名)如图,OC是∠AOB的平分线,P是OC上一点,PD⊥OA于点D,PD=6,则点P到边OB的距离为( )
A.6 B. 5 C. 4 D. 3
(1题图) (2题图) (3题图)
2.(2015 青岛)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. B. 2 C. 3 D. +2
3.(2015 湖州)如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
A.10 B. 7 C. 5 D. 4
4.(2015 丹东模拟)如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为( )
A. B. 2 C. 3 D. 2
(4题图) (5题图) (6题图)
5.(2015 高新区校级模拟)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和38,则△EDF的面积为( )
A.8 B. 12 C. 4 D. 6
6.(2015 从化市一模)如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
A.7 B. 6 C. 5 D. 4
7.(2015 河北模拟)如图,在四边形ABCD中,∠A=90°,AD=3,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
A.7.5 B. 8 C. 15 D. 无法确定
8.(2015 威海模拟)如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,BD平分∠ABC,E是AB中点,连接DE,则DE的长为( )
A. B. 2 C. D.
(7题图) (8题图) (9题图)
9.(2015春 黔西县期末)如图,直线l、l′、l″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处 B. 二处 C. 三处 D. 四处
10.(2015春 泰山区期末)如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
A.12 B. 18 C. 20 D. 24
(10题图) (11题图) (12题图)
二.填空题(共10小题)
11.(2015 聊城)如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若AB=6,则点D到AB的距离是 .
12.(2015 广西)如图,在△ABC中,CD平分∠ACB交AB于点D,DE⊥AC交于点E,DF⊥BC于点F,且BC=4,DE=2,则△BCD的面积是 .
13.(2015 萝岗区一模)如图,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,若AB=4,且点D到BC的距离为3,则BD= .
(13题图) (14题图) (15题图)
14.(2015 绿园区一模)如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为 .
15.(2014春 张家港市期末)如图所示在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥BA于E,AB=6厘米,则△DEB的周长是 厘米.
16.(2014秋 铜陵期末)如图,在△ABC中,∠BAC=50°,AD为∠BAC的平分线,DE⊥AB,DF⊥AC,则∠DEF= .
17.(2014秋 海珠区期末)如图,∠AOB=30°,OP平分∠AOB,PD⊥OB于D,PC∥OB交OA于C,若PC=6,则PD= .
(16题图) (17题图) (18题图)
18.(2015 徐州)如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A= °.
19.(2015春 邳州市期末)如图,在△ABC中,AB=AC,∠A=20°,边AC的垂直平分线交AC于点D,交AB于点E,则∠BCE等于 °.
(19题图) (20题图)
20.(2015 忻州校级模拟)如图,在Rt△ABC中,∠A=90°,∠ABC的平分线BD交AC于点D,AD=2,BC=9,则△BDC的面积是 .
三.解答题(共4小题)
21.(2015春 泰山区期末)如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.
22.(2015春 福鼎市校级月考)如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.
23.(2014秋 日照期末)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是28cm2,AB=16cm,AC=12cm,求DE的长.
24.(2014秋 莘县期末)如图,在△ABC中,AD平分∠BAC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,求证:AD⊥EF.
青岛版八年级上册第2章2.5角平分线的性质同步训练题参考答案
一.选择题(共10小题)
1.A 2.C 3.C 4.C 5.D 6.D 7.A 8.A 9.D 10.D
二.填空题(共10小题)
11. 12.4 13.5 14.8 15.6 16.25° 17.3
18.87 19.60 20.9
三.解答题(共4小题)
21.(1)证明:∵在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB,
∴CD=DE,∠AED=∠C=90°,∠CAD=∠EAD,
在△ACD和△AED中∴△ACD≌△AED,∴AC=AE;
(2)解:∵DE⊥AB,点E为AB的中点,∴AD=BD,
∴∠B=∠DAB=∠CAD,
∵∠C=90°,
∴3∠B=90°,
∴∠B=30°,
∵CD=DE=4,∠DEB=90°,
∴BD=2DE=8,
由勾股定理得:BE==4.
22.解:(1)∠PCD=∠PDC.
理由:∵OP是∠AOB的平分线,
且PC⊥OA,PD⊥OB,
∴PC=PD,
∴∠PCD=∠PDC;
(2)OP是CD的垂直平分线.
理由:∵∠OCP=∠ODP=90°,
在Rt△POC和Rt△POD中,
,
∴Rt△POC≌Rt△POD(HL),
∴OC=OD,
由PC=PD,OC=OD,可知点O、P都是线段CD的垂直平分线上的点,
从而OP是线段CD的垂直平分线.
23.∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∵S△ABC=S△ABD+S△ACD=AB×DE+AC×DF
∴S△ABC=(AB+AC)×DE
即×(16+12)×DE=28,
故DE=2(cm).
24.证明:∵AD平分∠BAC,
∴∠EAD=∠FAD,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD.
在△AED和△AFD中,
,
∴△AED≌△AFD(AAS),
∴AE=AF,
∵AD平分∠BAC,
∴AD⊥EF.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
