陕西省西安市阎良区重点中学2023-2024学年九年级下学期开学考试数学试题(含答案)
文档属性
| 名称 | 陕西省西安市阎良区重点中学2023-2024学年九年级下学期开学考试数学试题(含答案) | 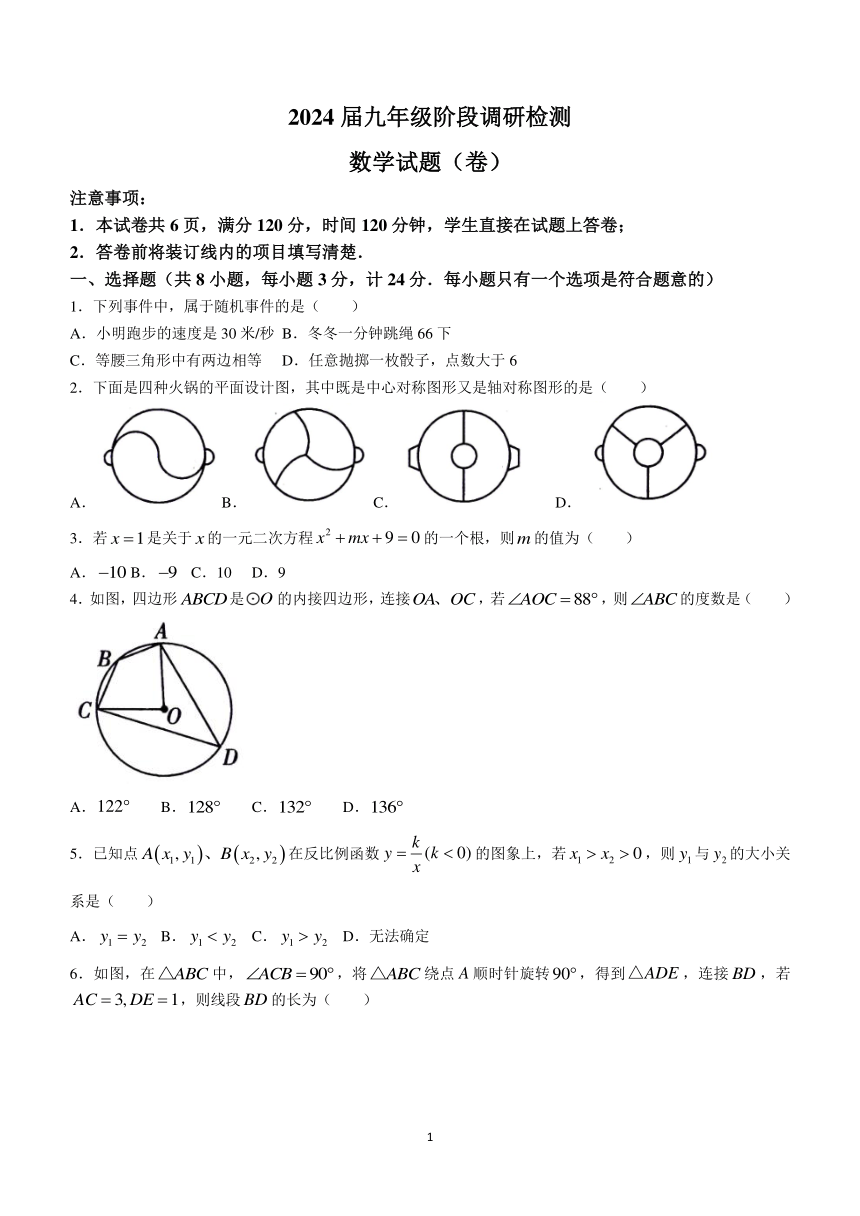 | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 20:27:17 | ||
图片预览




文档简介
2024届九年级阶段调研检测
数学试题(卷)
注意事项:
1.本试卷共6页,满分120分,时间120分钟,学生直接在试题上答卷;
2.答卷前将装订线内的项目填写清楚.
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.下列事件中,属于随机事件的是( )
A.小明跑步的速度是30米/秒 B.冬冬一分钟跳绳66下
C.等腰三角形中有两边相等 D.任意抛掷一枚骰子,点数大于6
2.下面是四种火锅的平面设计图,其中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
3.若是关于的一元二次方程的一个根,则的值为( )
A. B. C.10 D.9
4.如图,四边形是的内接四边形,连接,若,则的度数是( )
A. B. C. D.
5.已知点在反比例函数的图象上,若,则与的大小关系是( )
A. B. C. D.无法确定
6.如图,在中,,将绕点顺时针旋转,得到,连接,若,则线段的长为( )
A.6 B. C.. D.
7.如图的工件槽的两个底角均为,尺寸如图(单位),将形状规则的圆形铁片(如图所示)放入槽内,若同时有三个接触点,则该圆形铁片的半径是( )
A. B. C. D.
7.已知抛物线经过和,则抛物线的最低点的坐标为( )
A. B. C. D.
二、填空题(共5小题,每小题3分,计15分)
9.一元二次方程的根为________.
10.如图,为一个正多边形的顶点,为正多边形的中心.若,则这个正多边形的边数为________.
11.在一个不透明的口袋中,装有红色、黑色、白色的小球共40个,除颜色外其他完全相同,任意摸出一个球,记下颜色,放回后搅匀,重复上述过程,通过多次摸球试验后,摸到红色、黑色小球的频率分别稳定在0.25和0.45,则口袋中白球的个数可能是________.
12.如图,在平面直角坐标系中,点的坐标为轴于点,连接,反比例函数与的两条边分别交于两点,若点是的中点,连接,则的面积为________.
13.如图,在中,,点是线段上一动点,将绕点按顺时针方向旋转,得到,点是线段的中点,则长度的最小值为________.
三、解答题(共13小题,计81分.解答应写出过程)
14.(5分)解方程:.
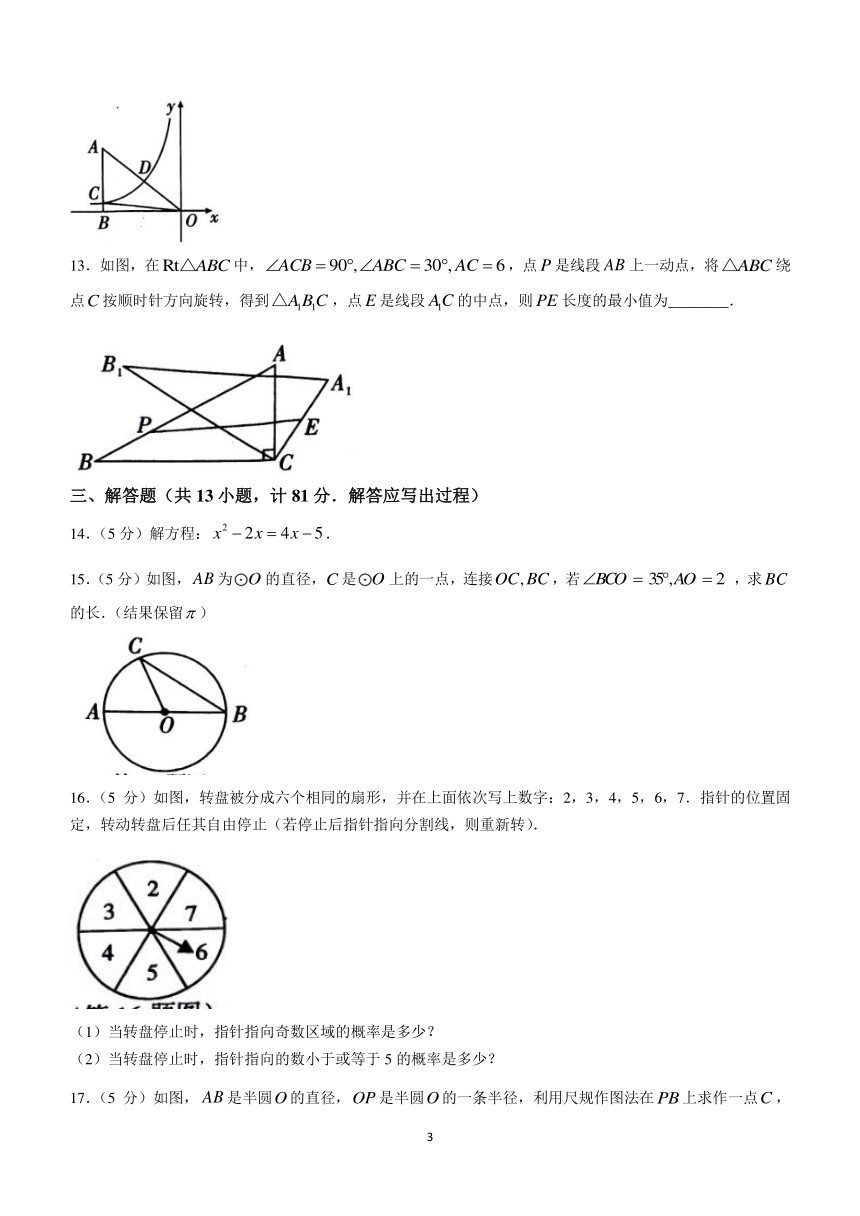
15.(5分)如图,为的直径,是上的一点,连接,若,求的长.(结果保留)
16.(5分)如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止(若停止后指针指向分割线,则重新转).
(1)当转盘停止时,指针指向奇数区域的概率是多少?
(2)当转盘停止时,指针指向的数小于或等于5的概率是多少?
17.(5分)如图,是半圆的直径,是半圆的一条半径,利用尺规作图法在上求作一点,连接,使得.(不写作法,保留作图痕迹)
18.(5分)如图,将绕点顺时针旋转得到,使点的对应点落在边上.若,连接,求的度数.
19.(5分)北京时间2023年12月27日14时50分,我国在酒泉卫星发射中心使用快舟一号甲运载火箭,成功将天目一号气象星座1922星发射升空,卫星顺利进入预定轨道,发射任务获得圆满成功.小明和小亮对航天知识都非常感兴趣,他们在中国载人航天网站上了解到,航天知识分为“梦圆天路”“飞天英雄”“探秘太空”“巡天飞船”等模块.他们决定从“梦圆天路”“飞天英雄”“探秘太空”“巡天飞船”四个模块中各自随机选择一个进行学习,设这四个模块依次为.
(1)小明选择学习“梦圆天路”模块的概率为________;
(2)请用画树状图或列表的方法,求小明和小亮选择不同模块的概率.
20.(5分)如图,在平面直角坐标系中,的顶点的坐标为.
(1)以为旋转中心,将顺时针旋转得到,画出,点的对应点分别为;
(2)在(1)的条件下,写出点的坐标.
21.(6分)若以30升/分钟的速度向一个空水池内注水,40分钟可以注满水池,设注水的速度为升/分钟,注满水池需要分钟.
(1)写出与之间的函数关系式;
(2)若小明的爸爸用24分钟就将这个空水池注满水,求注水的速度.
22.(7分)陕西肉夹馍全国闻名,某小吃店平均每天可卖出150个肉夹馍,卖出1个肉夹馍的利润是6元.经调查发现,每个肉夹馍每降价0.5元,平均每天可多卖出25个,为了使每天获取的利润更多,该小吃店决定把零售单价适当下调.在不考虑其他因素的条件下,求降价多少元时,能保证该小吃店每天获取的利润是1000元且卖出的肉夹馍更多?
23.(7分)已知抛物线(是常数).
(1)求证:该抛物线的顶点在函数的图象上;
(2)若点在该抛物线上,且,求的取值范围.
24.(8分)如图,是的直径,是的弦,,垂足是点,过点作直线交的延长线于点,且.
(1)求证:是的切线;
(2)如果,求的长.
25.(8分)图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点处,石块从投石机竖直方向上的点处被投出,已知石块运动轨迹所在抛物线的顶点坐标是.
(1)求抛物线的解析式;
(2)在斜坡上的点处建有垂直于水平线的城墙,且,点在一条直线上.通过计算说明石块能否飞越城墙.
26.(10分)【定义新知】
如图1,是上两点,且在直径的上方,若直径上存在一点,连接,满足,则称是的“幸运角”.
【问题探究】
(1)如图2,是的直径,弦是上的一点,连接交于点,连接.
①是的“幸运角”吗?请说明理由;
②设所对的圆心角为,请用含的式子表示的“幸运角”的度数;
【拓展延伸】
(2)如图3,在(1)的条件下,若直径,的“幸运角”为,,求的长.
2024届九年级阶段调研检测
数学试题参考答案及评分标准
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.B 2.C 3.A 4.D 5.C 6.B 7.A 8.D
二、填空题(共5小题,每小题3分,计15分)
9. 10.9 11.12 12.6 13.
三、解答题(共13小题,计81分.解答应写出过程)
14.解:整理得,
,
,
则,
.
注:其他解法正确也可.
15.解:,
,
,
的长.
16.解:(1)当转盘停止转动时,指针指向数字2,3,4,5,6,7区域的机会是均等的,共有6种均等的结果,其中指针指向奇数区域的共有3种结果,
当转盘停止时,指针指向奇数区域的概率是.
(2)当转盘停止转动时,指针指向数字2,3,4,5,6,7区域的机会是均等的,共有6种均等的结果,其中均等指针指向的数小于或等于5的区域共有4种结果,
当转盘停止时,指针指向的数小于或等于5的概率是.
17.解:如图所示,点即为所求.
18.解:,
.
绕点顺时针旋转得到,
,
.
19.解:(1).
(2)画树状图如下:
共有16种等可能的结果,其中小明和小亮选择不同模块的有12种,
所以小明和小亮选择不同模块的概率为.
20.解:(1)如图所示:
(2)点的坐标为.
21.解:(1)由题意得,
则,
与之间的函数关系式为.
(2)当时,有,
解得,
注水的速度为50升/分钟.
22.解:设每个肉夹馍应降价元,
根据题意可得,
整理,得,
解得,
当时,卖出的肉夹谟为(个),
当时,卖出的肉夹馍为(个).
,
.
答:降价2元时,能保证该小吃店每天获取的利润是1000元且卖出的肉夹馍更多.
23.(1)证明:,
抛物线的顶点坐标为,
当时,,
抛物线的顶点在函数的图象上.
(2)解:由题意可得,
.
,
,
解得.
的取值范围是.
24.(1)证明:连接,则.
,
,则.
,
,
,即,
是的切线.
(2)解:,
,
4,
,
.
25.解:(1)由题意得:抛物线的顶点坐标是,点的坐标为.
设抛物线的解析式为,
将代入,得,
解得,
抛物线的解析式为.
(2),
点的横坐标为75.
将代入,得.
,
.
,
石块不能飞越城墙.
26.解:(1)①是的“幸运角”.
理由:是的直径,弦,
,
.
,
,
是的“幸运角”.
(2)所对的圆心角为,
.
,
,
,
的“幸运角”的度数为.
(2)连接,如图3,
的“幸运角”为,
.
由(1)知,
,则.
,
,
.
设,则,
,
解得:,
或.
数学试题(卷)
注意事项:
1.本试卷共6页,满分120分,时间120分钟,学生直接在试题上答卷;
2.答卷前将装订线内的项目填写清楚.
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.下列事件中,属于随机事件的是( )
A.小明跑步的速度是30米/秒 B.冬冬一分钟跳绳66下
C.等腰三角形中有两边相等 D.任意抛掷一枚骰子,点数大于6
2.下面是四种火锅的平面设计图,其中既是中心对称图形又是轴对称图形的是( )
A. B. C. D.
3.若是关于的一元二次方程的一个根,则的值为( )
A. B. C.10 D.9
4.如图,四边形是的内接四边形,连接,若,则的度数是( )
A. B. C. D.
5.已知点在反比例函数的图象上,若,则与的大小关系是( )
A. B. C. D.无法确定
6.如图,在中,,将绕点顺时针旋转,得到,连接,若,则线段的长为( )
A.6 B. C.. D.
7.如图的工件槽的两个底角均为,尺寸如图(单位),将形状规则的圆形铁片(如图所示)放入槽内,若同时有三个接触点,则该圆形铁片的半径是( )
A. B. C. D.
7.已知抛物线经过和,则抛物线的最低点的坐标为( )
A. B. C. D.
二、填空题(共5小题,每小题3分,计15分)
9.一元二次方程的根为________.
10.如图,为一个正多边形的顶点,为正多边形的中心.若,则这个正多边形的边数为________.
11.在一个不透明的口袋中,装有红色、黑色、白色的小球共40个,除颜色外其他完全相同,任意摸出一个球,记下颜色,放回后搅匀,重复上述过程,通过多次摸球试验后,摸到红色、黑色小球的频率分别稳定在0.25和0.45,则口袋中白球的个数可能是________.
12.如图,在平面直角坐标系中,点的坐标为轴于点,连接,反比例函数与的两条边分别交于两点,若点是的中点,连接,则的面积为________.
13.如图,在中,,点是线段上一动点,将绕点按顺时针方向旋转,得到,点是线段的中点,则长度的最小值为________.
三、解答题(共13小题,计81分.解答应写出过程)
14.(5分)解方程:.
15.(5分)如图,为的直径,是上的一点,连接,若,求的长.(结果保留)
16.(5分)如图,转盘被分成六个相同的扇形,并在上面依次写上数字:2,3,4,5,6,7.指针的位置固定,转动转盘后任其自由停止(若停止后指针指向分割线,则重新转).
(1)当转盘停止时,指针指向奇数区域的概率是多少?
(2)当转盘停止时,指针指向的数小于或等于5的概率是多少?
17.(5分)如图,是半圆的直径,是半圆的一条半径,利用尺规作图法在上求作一点,连接,使得.(不写作法,保留作图痕迹)
18.(5分)如图,将绕点顺时针旋转得到,使点的对应点落在边上.若,连接,求的度数.
19.(5分)北京时间2023年12月27日14时50分,我国在酒泉卫星发射中心使用快舟一号甲运载火箭,成功将天目一号气象星座1922星发射升空,卫星顺利进入预定轨道,发射任务获得圆满成功.小明和小亮对航天知识都非常感兴趣,他们在中国载人航天网站上了解到,航天知识分为“梦圆天路”“飞天英雄”“探秘太空”“巡天飞船”等模块.他们决定从“梦圆天路”“飞天英雄”“探秘太空”“巡天飞船”四个模块中各自随机选择一个进行学习,设这四个模块依次为.
(1)小明选择学习“梦圆天路”模块的概率为________;
(2)请用画树状图或列表的方法,求小明和小亮选择不同模块的概率.
20.(5分)如图,在平面直角坐标系中,的顶点的坐标为.
(1)以为旋转中心,将顺时针旋转得到,画出,点的对应点分别为;
(2)在(1)的条件下,写出点的坐标.
21.(6分)若以30升/分钟的速度向一个空水池内注水,40分钟可以注满水池,设注水的速度为升/分钟,注满水池需要分钟.
(1)写出与之间的函数关系式;
(2)若小明的爸爸用24分钟就将这个空水池注满水,求注水的速度.
22.(7分)陕西肉夹馍全国闻名,某小吃店平均每天可卖出150个肉夹馍,卖出1个肉夹馍的利润是6元.经调查发现,每个肉夹馍每降价0.5元,平均每天可多卖出25个,为了使每天获取的利润更多,该小吃店决定把零售单价适当下调.在不考虑其他因素的条件下,求降价多少元时,能保证该小吃店每天获取的利润是1000元且卖出的肉夹馍更多?
23.(7分)已知抛物线(是常数).
(1)求证:该抛物线的顶点在函数的图象上;
(2)若点在该抛物线上,且,求的取值范围.
24.(8分)如图,是的直径,是的弦,,垂足是点,过点作直线交的延长线于点,且.
(1)求证:是的切线;
(2)如果,求的长.
25.(8分)图①是古代的一种远程投石机,其投出去的石块运动轨迹是抛物线的一部分.据《范蠡兵法》记载:“飞石重十二斤,为机发,行二百步”,其原理蕴含了物理中的“杠杆原理”.在如图②所示的平面直角坐标系中,将投石机置于斜坡的底部点处,石块从投石机竖直方向上的点处被投出,已知石块运动轨迹所在抛物线的顶点坐标是.
(1)求抛物线的解析式;
(2)在斜坡上的点处建有垂直于水平线的城墙,且,点在一条直线上.通过计算说明石块能否飞越城墙.
26.(10分)【定义新知】
如图1,是上两点,且在直径的上方,若直径上存在一点,连接,满足,则称是的“幸运角”.
【问题探究】
(1)如图2,是的直径,弦是上的一点,连接交于点,连接.
①是的“幸运角”吗?请说明理由;
②设所对的圆心角为,请用含的式子表示的“幸运角”的度数;
【拓展延伸】
(2)如图3,在(1)的条件下,若直径,的“幸运角”为,,求的长.
2024届九年级阶段调研检测
数学试题参考答案及评分标准
一、选择题(共8小题,每小题3分,计24分.每小题只有一个选项是符合题意的)
1.B 2.C 3.A 4.D 5.C 6.B 7.A 8.D
二、填空题(共5小题,每小题3分,计15分)
9. 10.9 11.12 12.6 13.
三、解答题(共13小题,计81分.解答应写出过程)
14.解:整理得,
,
,
则,
.
注:其他解法正确也可.
15.解:,
,
,
的长.
16.解:(1)当转盘停止转动时,指针指向数字2,3,4,5,6,7区域的机会是均等的,共有6种均等的结果,其中指针指向奇数区域的共有3种结果,
当转盘停止时,指针指向奇数区域的概率是.
(2)当转盘停止转动时,指针指向数字2,3,4,5,6,7区域的机会是均等的,共有6种均等的结果,其中均等指针指向的数小于或等于5的区域共有4种结果,
当转盘停止时,指针指向的数小于或等于5的概率是.
17.解:如图所示,点即为所求.
18.解:,
.
绕点顺时针旋转得到,
,
.
19.解:(1).
(2)画树状图如下:
共有16种等可能的结果,其中小明和小亮选择不同模块的有12种,
所以小明和小亮选择不同模块的概率为.
20.解:(1)如图所示:
(2)点的坐标为.
21.解:(1)由题意得,
则,
与之间的函数关系式为.
(2)当时,有,
解得,
注水的速度为50升/分钟.
22.解:设每个肉夹馍应降价元,
根据题意可得,
整理,得,
解得,
当时,卖出的肉夹谟为(个),
当时,卖出的肉夹馍为(个).
,
.
答:降价2元时,能保证该小吃店每天获取的利润是1000元且卖出的肉夹馍更多.
23.(1)证明:,
抛物线的顶点坐标为,
当时,,
抛物线的顶点在函数的图象上.
(2)解:由题意可得,
.
,
,
解得.
的取值范围是.
24.(1)证明:连接,则.
,
,则.
,
,
,即,
是的切线.
(2)解:,
,
4,
,
.
25.解:(1)由题意得:抛物线的顶点坐标是,点的坐标为.
设抛物线的解析式为,
将代入,得,
解得,
抛物线的解析式为.
(2),
点的横坐标为75.
将代入,得.
,
.
,
石块不能飞越城墙.
26.解:(1)①是的“幸运角”.
理由:是的直径,弦,
,
.
,
,
是的“幸运角”.
(2)所对的圆心角为,
.
,
,
,
的“幸运角”的度数为.
(2)连接,如图3,
的“幸运角”为,
.
由(1)知,
,则.
,
,
.
设,则,
,
解得:,
或.
同课章节目录
