青岛版九年级数学上册第1章1.1相似多边形同步训练题(含答案)
文档属性
| 名称 | 青岛版九年级数学上册第1章1.1相似多边形同步训练题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 90.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-19 00:00:00 | ||
图片预览

文档简介
青岛版九年级数学上册第1章1.1相似多边形同步训练题(含答案)
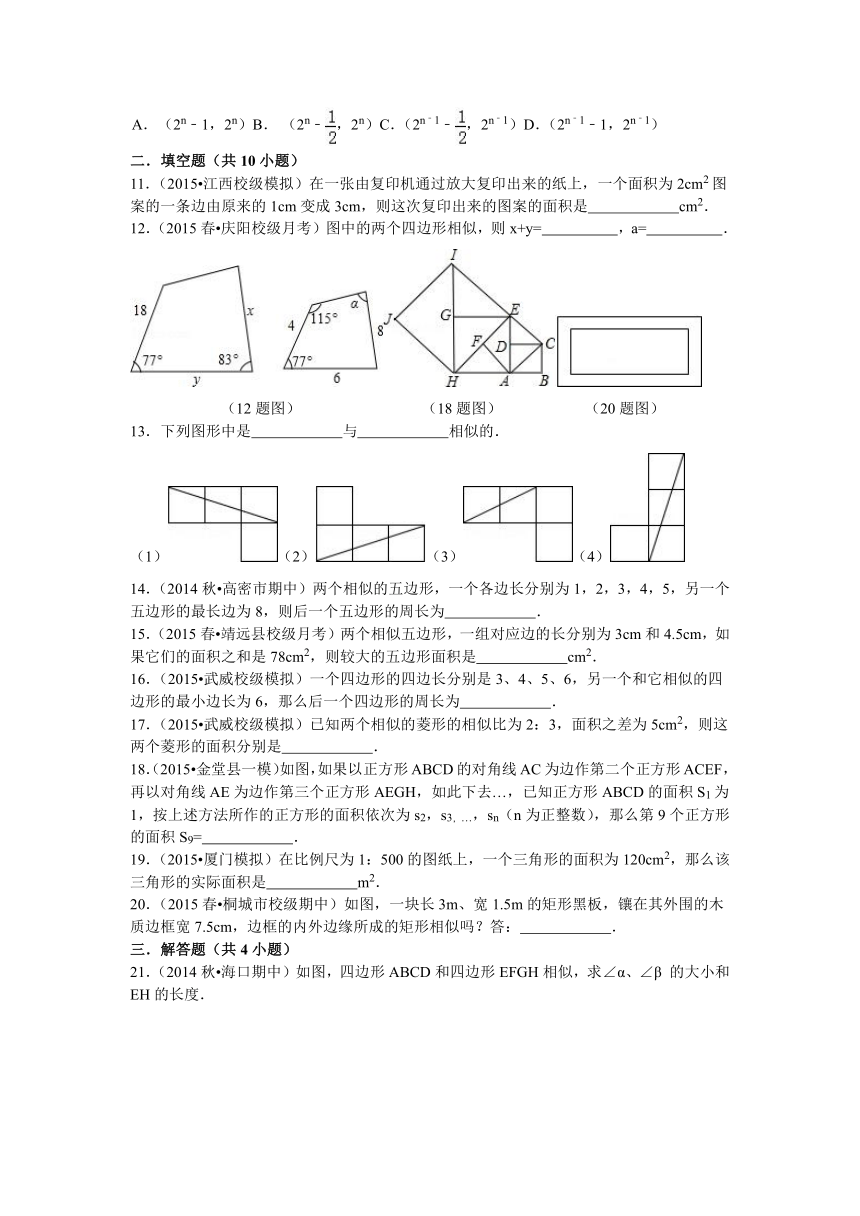
一.选择题(共10小题)
1.(2014秋 遂宁期末)下列判断正确的是( )
A. 所有的直角三角形都相似 B. 所有的等腰直角三角形都相似
C. 所有的菱形都相似 D. 所有的矩形都相似
2.(2014秋 滨江区期末)下列各组中的两个图形,一定相似的是( )
A. 有一个角对应相等的两个菱形 B. 对应边成比例的两个多边形
C. 两条对角线对应成比例的两个平行四边形 D. 任意两个矩形
3.(2014秋 扬州月考)下列四组图形中,不是相似图形的是( )
A. B.C.D.
4.(2014秋 聊城校级月考)用一个4倍的放大镜去放大△ABC,下列说法正确的是( )
A. △ABC放大后,∠A是原来的4倍 B. △ABC放大后,周长是原来的4倍
C. △ABC放大后,面积是原来的4倍 D. 以上说法都不正确
5.(2015 杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
A.10 B. 12 C. D.
(5题图) (10题图)
6.(2015春 泰山区期末)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.B. C.D.
7.(2015 长沙一模)两个相似多边形的面积之比为1:9,则它们的周长之比为( )
A.1:3 B. 1:9 C. 1: D. 2:3
8.(2014 鄂州三模)如果两个相似多边形的面积比为16:9,那么这两个相似多边形的相似比为( )
A.16:9 B. 4:3 C. 2:3 D. 256:81
9.(2015春 高密市期末)已知两个五边形相似,其中一个五边形的最长边为20,最短边为4,另一个五边形的最短边为3,则它的最长边为( )
A.15 B. 12 C. 9 D. 6
10.(2014 杭州模拟)彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
A. (2n﹣1,2n)B. (2n﹣,2n)C.(2n﹣1﹣,2n﹣1)D.(2n﹣1﹣1,2n﹣1)
二.填空题(共10小题)
11.(2015 江西校级模拟)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是 cm2.
12.(2015春 庆阳校级月考)图中的两个四边形相似,则x+y= ,a= .
(12题图) (18题图) (20题图)
13.下列图形中是 与 相似的.
(1)(2)(3)(4)
14.(2014秋 高密市期中)两个相似的五边形,一个各边长分别为1,2,3,4,5,另一个五边形的最长边为8,则后一个五边形的周长为 .
15.(2015春 靖远县校级月考)两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则较大的五边形面积是 cm2.
16.(2015 武威校级模拟)一个四边形的四边长分别是3、4、5、6,另一个和它相似的四边形的最小边长为6,那么后一个四边形的周长为 .
17.(2015 武威校级模拟)已知两个相似的菱形的相似比为2:3,面积之差为5cm2,则这两个菱形的面积分别是 .
18.(2015 金堂县一模)如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为s2,s3,…,sn(n为正整数),那么第9个正方形的面积S9= .
19.(2015 厦门模拟)在比例尺为1:500的图纸上,一个三角形的面积为120cm2,那么该三角形的实际面积是 m2.
20.(2015春 桐城市校级期中)如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?答: .
三.解答题(共4小题)
21.(2014秋 海口期中)如图,四边形ABCD和四边形EFGH相似,求∠α、∠β 的大小和EH的长度.
22.(2012春 新浦区校级期中)如图:矩形草坪的长为a米,宽为b米(a>b),沿草坪四周外围有宽为x米的环形小路.
(1)草坪的长与宽的比值m= ,外围矩形的长与宽的比值n= .(用含有a、b、x的代数式表示);
(2)请比较m与n的大小;
(3)图中的两个矩形相似吗?为什么?
23.(2007 宁波)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
24.如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.
青岛版九年级数学上册第1章1.1相似多边形同步训练题参考答案
一.选择题(共10小题)
1.B 2.A 3.D 4.B 5.C 6.B 7.A 8.B 9.A 10.A
二.填空题(共10小题)
11.18 12.6385° 13.(1)(4) 14.24 15.54 16.36
17.4cm2,9cm2 18.256 19.3000 20.不相似
三.解答题(共4小题)
21.解:∵四边形ABCD和四边形EFGH相似,
∴∠α=∠B=83°,∠D=∠H=118°,∠β=360°﹣(83°+78°+118°)=81°,EH:AD=HG:DC,
∴=,
∴EH=28(cm).
答:∠α=83°,∠β=81°,EH=28cm.
22.解:(1)∵矩形草坪的长为a米,宽为b米(a>b),
∴草坪的长与宽的比值m=a:b,
外围矩形的长与宽的比值n=(a+2x):(b+2x);
(2)m﹣n=﹣==,
∵a>b>0,
∴m﹣n=>0,
∴m>n;
(3)若图中的两个矩形相似,则需m=n,
∵m>n,
∴图中的两个矩形不相似.
故答案为:(1)a:b,(a+2x):(b+2x).
23.解:(1)由已知得MN=AB,MD=AD=BC,
∵矩形DMNC与矩形ABCD相似,
,
∵MN=AB,DM=AD,BC=AD,
∴AD2=AB2,
∴由AB=4得,AD=4;
(2)矩形DMNC与矩形ABCD的相似比为=.
24.解:四边形ABCD与四边形AEOF相似,理由如下:
∵△AEO∽△ABC,
∴∠2=∠1,∠4=∠3,==,
∵△AOF∽△ACD,
∴∠6=∠5,∠8=∠7,==,
∴∠2+∠6=∠1+∠5,即∠EOF=∠BCD,===.
在四边形AEOF与四边形ABCD中,
∵∠EAF=∠BAD,∠4=∠3,∠EOF=∠BCD,∠8=∠7,
===,
∴四边形AEOF∽四边形ABCD,
即四边形ABCD与四边形AEOF相似.
一.选择题(共10小题)
1.(2014秋 遂宁期末)下列判断正确的是( )
A. 所有的直角三角形都相似 B. 所有的等腰直角三角形都相似
C. 所有的菱形都相似 D. 所有的矩形都相似
2.(2014秋 滨江区期末)下列各组中的两个图形,一定相似的是( )
A. 有一个角对应相等的两个菱形 B. 对应边成比例的两个多边形
C. 两条对角线对应成比例的两个平行四边形 D. 任意两个矩形
3.(2014秋 扬州月考)下列四组图形中,不是相似图形的是( )
A. B.C.D.
4.(2014秋 聊城校级月考)用一个4倍的放大镜去放大△ABC,下列说法正确的是( )
A. △ABC放大后,∠A是原来的4倍 B. △ABC放大后,周长是原来的4倍
C. △ABC放大后,面积是原来的4倍 D. 以上说法都不正确
5.(2015 杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是( )
A.10 B. 12 C. D.
(5题图) (10题图)
6.(2015春 泰山区期末)如图所示,两个等边三角形,两个矩形,两个正方形,两个菱形各成一组,每组中的一个图形在另一个图形的内部,对应边平行,且对应边之间的距离都相等,那么两个图形不相似的一组是( )
A.B. C.D.
7.(2015 长沙一模)两个相似多边形的面积之比为1:9,则它们的周长之比为( )
A.1:3 B. 1:9 C. 1: D. 2:3
8.(2014 鄂州三模)如果两个相似多边形的面积比为16:9,那么这两个相似多边形的相似比为( )
A.16:9 B. 4:3 C. 2:3 D. 256:81
9.(2015春 高密市期末)已知两个五边形相似,其中一个五边形的最长边为20,最短边为4,另一个五边形的最短边为3,则它的最长边为( )
A.15 B. 12 C. 9 D. 6
10.(2014 杭州模拟)彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
A. (2n﹣1,2n)B. (2n﹣,2n)C.(2n﹣1﹣,2n﹣1)D.(2n﹣1﹣1,2n﹣1)
二.填空题(共10小题)
11.(2015 江西校级模拟)在一张由复印机通过放大复印出来的纸上,一个面积为2cm2图案的一条边由原来的1cm变成3cm,则这次复印出来的图案的面积是 cm2.
12.(2015春 庆阳校级月考)图中的两个四边形相似,则x+y= ,a= .
(12题图) (18题图) (20题图)
13.下列图形中是 与 相似的.
(1)(2)(3)(4)
14.(2014秋 高密市期中)两个相似的五边形,一个各边长分别为1,2,3,4,5,另一个五边形的最长边为8,则后一个五边形的周长为 .
15.(2015春 靖远县校级月考)两个相似五边形,一组对应边的长分别为3cm和4.5cm,如果它们的面积之和是78cm2,则较大的五边形面积是 cm2.
16.(2015 武威校级模拟)一个四边形的四边长分别是3、4、5、6,另一个和它相似的四边形的最小边长为6,那么后一个四边形的周长为 .
17.(2015 武威校级模拟)已知两个相似的菱形的相似比为2:3,面积之差为5cm2,则这两个菱形的面积分别是 .
18.(2015 金堂县一模)如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为s2,s3,…,sn(n为正整数),那么第9个正方形的面积S9= .
19.(2015 厦门模拟)在比例尺为1:500的图纸上,一个三角形的面积为120cm2,那么该三角形的实际面积是 m2.
20.(2015春 桐城市校级期中)如图,一块长3m、宽1.5m的矩形黑板,镶在其外围的木质边框宽7.5cm,边框的内外边缘所成的矩形相似吗?答: .
三.解答题(共4小题)
21.(2014秋 海口期中)如图,四边形ABCD和四边形EFGH相似,求∠α、∠β 的大小和EH的长度.
22.(2012春 新浦区校级期中)如图:矩形草坪的长为a米,宽为b米(a>b),沿草坪四周外围有宽为x米的环形小路.
(1)草坪的长与宽的比值m= ,外围矩形的长与宽的比值n= .(用含有a、b、x的代数式表示);
(2)请比较m与n的大小;
(3)图中的两个矩形相似吗?为什么?
23.(2007 宁波)如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,已知AB=4.
(1)求AD的长;
(2)求矩形DMNC与矩形ABCD的相似比.
24.如图,已知△AEO∽△ABC,△AOF∽△ACD,那么四边形ABCD与四边形AEOF相似吗?请说明你的理由.
青岛版九年级数学上册第1章1.1相似多边形同步训练题参考答案
一.选择题(共10小题)
1.B 2.A 3.D 4.B 5.C 6.B 7.A 8.B 9.A 10.A
二.填空题(共10小题)
11.18 12.6385° 13.(1)(4) 14.24 15.54 16.36
17.4cm2,9cm2 18.256 19.3000 20.不相似
三.解答题(共4小题)
21.解:∵四边形ABCD和四边形EFGH相似,
∴∠α=∠B=83°,∠D=∠H=118°,∠β=360°﹣(83°+78°+118°)=81°,EH:AD=HG:DC,
∴=,
∴EH=28(cm).
答:∠α=83°,∠β=81°,EH=28cm.
22.解:(1)∵矩形草坪的长为a米,宽为b米(a>b),
∴草坪的长与宽的比值m=a:b,
外围矩形的长与宽的比值n=(a+2x):(b+2x);
(2)m﹣n=﹣==,
∵a>b>0,
∴m﹣n=>0,
∴m>n;
(3)若图中的两个矩形相似,则需m=n,
∵m>n,
∴图中的两个矩形不相似.
故答案为:(1)a:b,(a+2x):(b+2x).
23.解:(1)由已知得MN=AB,MD=AD=BC,
∵矩形DMNC与矩形ABCD相似,
,
∵MN=AB,DM=AD,BC=AD,
∴AD2=AB2,
∴由AB=4得,AD=4;
(2)矩形DMNC与矩形ABCD的相似比为=.
24.解:四边形ABCD与四边形AEOF相似,理由如下:
∵△AEO∽△ABC,
∴∠2=∠1,∠4=∠3,==,
∵△AOF∽△ACD,
∴∠6=∠5,∠8=∠7,==,
∴∠2+∠6=∠1+∠5,即∠EOF=∠BCD,===.
在四边形AEOF与四边形ABCD中,
∵∠EAF=∠BAD,∠4=∠3,∠EOF=∠BCD,∠8=∠7,
===,
∴四边形AEOF∽四边形ABCD,
即四边形ABCD与四边形AEOF相似.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
