人教版小学数学四年级下册3.1《 加法运算律》 课件(共29张PPT)
文档属性
| 名称 | 人教版小学数学四年级下册3.1《 加法运算律》 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 20:54:04 | ||
图片预览






文档简介
(共29张PPT)
第三单元 运算律
第1课时 加法运算律
你会骑自行车吗?一般在去多远的地方时,你会骑车前往呢?你会考虑骑自行车旅行吗?
说一说从题中你了解到哪些数学信息 需要解决什么问题
李叔叔计划骑车旅行一个星期。他今天上午骑了40km,下午骑了56km。李叔叔今天一共骑了多少千米?
1
上午骑了40千米
下午骑了56千米
李叔叔今天一共骑了多少千米?
已知条件
要解决的问题
李叔叔计划骑车旅行一个星期。他今天上午骑了40km,下午骑了56km。李叔叔今天一共骑了多少千米?
1
你是怎么解决这个问题的?
我用上午行程+下午行程=全天行程
下午行程+上午行程,同样是全天行程
小组讨论
40+56=96(km)
上午行程
全天行程
下午行程
+
=
56+40=96(km)
上午行程
全天行程
下午行程
+
=
说一说
观察两个算式,你发现了什么?
40+56=96
56+40=96
=
40+56
56+40
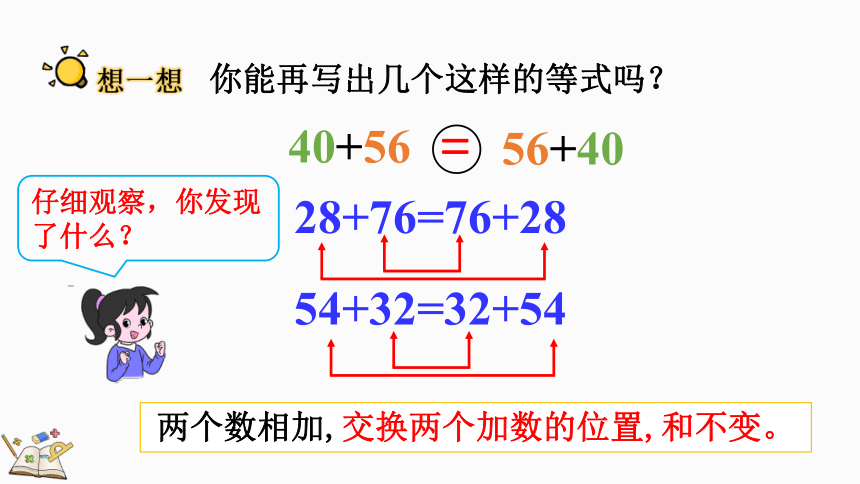
你能再写出几个这样的等式吗?
28+76=76+28
=
40+56
56+40
54+32=32+54
仔细观察,你发现了什么?
两个数相加,交换两个加数的位置,和不变。
想一想
两个数相加,交换两个加数的位置,
和不变。这叫作加法交换律。
小组讨论
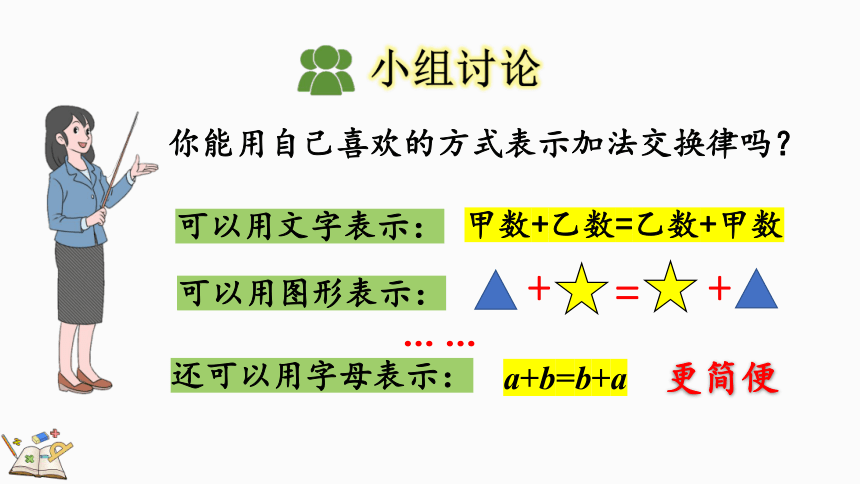
你能用自己喜欢的方式表示加法交换律吗?
甲数+乙数=乙数+甲数
a+b=b+a
更简便
可以用文字表示:
可以用图形表示:
还可以用字母表示:
+
=
+
… …
加法交换律用字母表示为:
a+b=b+a
两个数相加,交换两个加数的位置,
和不变。这叫作加法交换律。
下面是叔叔前三天的骑行情况。
第一天 第二天 第三天
88km 104km 96km
这三天李叔叔一共骑行了多少千米?
2
说一说从题中你了解到哪些数学信息 需要解决什么问题
第一天:
第二天:
第三天:
88km
104km
96km
已知数学信息:
要解决问题:
李叔叔三天一共骑行了多少千米?
2
下面是叔叔前三天的骑行情况。
第一天 第二天 第三天
88km 104km 96km
这三天李叔叔一共骑行了多少千米?
说一说,你是如何解决问题的
我先算出前两天骑行的路程,再加第三天骑行的路程。
88 + 104 + 96
答:这三天李叔叔一共骑了288千米。
= 192 + 96
= 288(km)
我先算出后两天骑行的路程,再加第一天骑行的路程。
88 +(104 + 96)
= 88 + 200
= 288(km)
答:这三天李叔叔一共骑了288千米。
=88+200
=288
88+104 +96
88+(104+96)
=192+96
=288
(69+176)+28 69+(176+28)
155+(145+207) (155+145)+207
=
=
你还能写出像这样的等式吗?
( )
先把后两个数相加
结果相等
观察两个算式,你发现了什么?
先把前两个数相加
说一说
(69+176)+28 69+(176+28)
=
=
小组讨论
比较下面的两组算式,你发现了什么?
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
155+(145+207) (155+145)+207
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫作加法结合律。
小组讨论
你能用符号表示加法结合律吗?
更简便
(a+b)+c=a+(b+c)
……
( + )+ = +( + )
加法结合律用字母表示为:
(a+b)+c=a+(b+c)
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫作加法结合律。
选自教材第18页做一做第1题
1
根据加法交换律填空。
300+600 = 600+____ ____+65 = 65+35
78+____ = 43+____ a+12 = 12+___
300
35
43
78
a
2
根据加法结合律填空。
(25+68)+32 = 25+(____+____)
130+(70+4) = (130+____)+___
68
32
70
4
把后两个数相加
先把前两个数相加
选自教材第18页做一做第2题
下面算式分别运用了什么运算律?
76+18=18+76
56+72+28=56+(72+28)
31+67+19=31+19+67
24+42+76+58=(24+76)+(42+58)
加法交换律
加法结合律
加法交换律
加法交换律和结合律
3
选自教材第19页练习五第1题
可以利用加法交换律直接得出答案。
填一填。
144
161
213
594
611
46
98
115
496
+
98
115
496
46
213
92
144
161
542
196
594
230
611
992
542
1.
125 – 8 – 25 = 125 – ( ) – 8
986 – 58 – 86 = 986 – ( ) – 58
25
86
在减法算式里可以交换
两个减数的位置。
2.
填一填。
○+△+□= ○ +(△+ )
□
△
○+△+□+△= ○ + □ +(△+ )
x+y+z+x= ( + )+y+z
x
x
这节课有什么收获呢?
两个数相加,交换加数的位置,和不变。
这叫作加法交换律。
用字母表示为:a+b=b+a
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫作加法结合律。
用字母表示为: (a+b)+c=a+(b+c)
1.教材第19页练习五第2~4题;
2.从课时练中选取。
加法运算律
a+b=b+a
(a+b)+c=a+(b+c)
加法交换律
加法结合律
第三单元 运算律
第1课时 加法运算律
你会骑自行车吗?一般在去多远的地方时,你会骑车前往呢?你会考虑骑自行车旅行吗?
说一说从题中你了解到哪些数学信息 需要解决什么问题
李叔叔计划骑车旅行一个星期。他今天上午骑了40km,下午骑了56km。李叔叔今天一共骑了多少千米?
1
上午骑了40千米
下午骑了56千米
李叔叔今天一共骑了多少千米?
已知条件
要解决的问题
李叔叔计划骑车旅行一个星期。他今天上午骑了40km,下午骑了56km。李叔叔今天一共骑了多少千米?
1
你是怎么解决这个问题的?
我用上午行程+下午行程=全天行程
下午行程+上午行程,同样是全天行程
小组讨论
40+56=96(km)
上午行程
全天行程
下午行程
+
=
56+40=96(km)
上午行程
全天行程
下午行程
+
=
说一说
观察两个算式,你发现了什么?
40+56=96
56+40=96
=
40+56
56+40
你能再写出几个这样的等式吗?
28+76=76+28
=
40+56
56+40
54+32=32+54
仔细观察,你发现了什么?
两个数相加,交换两个加数的位置,和不变。
想一想
两个数相加,交换两个加数的位置,
和不变。这叫作加法交换律。
小组讨论
你能用自己喜欢的方式表示加法交换律吗?
甲数+乙数=乙数+甲数
a+b=b+a
更简便
可以用文字表示:
可以用图形表示:
还可以用字母表示:
+
=
+
… …
加法交换律用字母表示为:
a+b=b+a
两个数相加,交换两个加数的位置,
和不变。这叫作加法交换律。
下面是叔叔前三天的骑行情况。
第一天 第二天 第三天
88km 104km 96km
这三天李叔叔一共骑行了多少千米?
2
说一说从题中你了解到哪些数学信息 需要解决什么问题
第一天:
第二天:
第三天:
88km
104km
96km
已知数学信息:
要解决问题:
李叔叔三天一共骑行了多少千米?
2
下面是叔叔前三天的骑行情况。
第一天 第二天 第三天
88km 104km 96km
这三天李叔叔一共骑行了多少千米?
说一说,你是如何解决问题的
我先算出前两天骑行的路程,再加第三天骑行的路程。
88 + 104 + 96
答:这三天李叔叔一共骑了288千米。
= 192 + 96
= 288(km)
我先算出后两天骑行的路程,再加第一天骑行的路程。
88 +(104 + 96)
= 88 + 200
= 288(km)
答:这三天李叔叔一共骑了288千米。
=88+200
=288
88+104 +96
88+(104+96)
=192+96
=288
(69+176)+28 69+(176+28)
155+(145+207) (155+145)+207
=
=
你还能写出像这样的等式吗?
( )
先把后两个数相加
结果相等
观察两个算式,你发现了什么?
先把前两个数相加
说一说
(69+176)+28 69+(176+28)
=
=
小组讨论
比较下面的两组算式,你发现了什么?
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
155+(145+207) (155+145)+207
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫作加法结合律。
小组讨论
你能用符号表示加法结合律吗?
更简便
(a+b)+c=a+(b+c)
……
( + )+ = +( + )
加法结合律用字母表示为:
(a+b)+c=a+(b+c)
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫作加法结合律。
选自教材第18页做一做第1题
1
根据加法交换律填空。
300+600 = 600+____ ____+65 = 65+35
78+____ = 43+____ a+12 = 12+___
300
35
43
78
a
2
根据加法结合律填空。
(25+68)+32 = 25+(____+____)
130+(70+4) = (130+____)+___
68
32
70
4
把后两个数相加
先把前两个数相加
选自教材第18页做一做第2题
下面算式分别运用了什么运算律?
76+18=18+76
56+72+28=56+(72+28)
31+67+19=31+19+67
24+42+76+58=(24+76)+(42+58)
加法交换律
加法结合律
加法交换律
加法交换律和结合律
3
选自教材第19页练习五第1题
可以利用加法交换律直接得出答案。
填一填。
144
161
213
594
611
46
98
115
496
+
98
115
496
46
213
92
144
161
542
196
594
230
611
992
542
1.
125 – 8 – 25 = 125 – ( ) – 8
986 – 58 – 86 = 986 – ( ) – 58
25
86
在减法算式里可以交换
两个减数的位置。
2.
填一填。
○+△+□= ○ +(△+ )
□
△
○+△+□+△= ○ + □ +(△+ )
x+y+z+x= ( + )+y+z
x
x
这节课有什么收获呢?
两个数相加,交换加数的位置,和不变。
这叫作加法交换律。
用字母表示为:a+b=b+a
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。这叫作加法结合律。
用字母表示为: (a+b)+c=a+(b+c)
1.教材第19页练习五第2~4题;
2.从课时练中选取。
加法运算律
a+b=b+a
(a+b)+c=a+(b+c)
加法交换律
加法结合律
