青岛版七年级下册11.2.2积的乘方与幂的乘方 课件(共14张PPT)
文档属性
| 名称 | 青岛版七年级下册11.2.2积的乘方与幂的乘方 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 21:19:25 | ||
图片预览






文档简介
(共14张PPT)
11.2.2积的乘方与幂的乘方
七年级下册第十一单元
复习回顾
1、同底数幂的乘法法则
am · an=am+n(m,n都是正整数)
2、积的乘方法则
(ab)n=anbn(n是正整数)
3、积的乘方逆运算
anbn=(ab)n(n是正整数)
1.能说出幂的乘方的运算性质,并会用符号表示;
2.能灵活运用幂的乘方法则进行计算,并能说出每一步运算的依据;
3.熟练运用法则解决问题。
学习目标
学习任务:
1.探索幂的乘方的运算性质
2.幂的乘方等运算性质的运用
=×6.373×(103)3
问题引入
地球可以近似地看做是球体,球的半径约为6.37×103 千米,它的体积大约是多少(精确到1010立方千米)?
提示:球的体积公式为 V= (r表示球的半径)
V= =×(6.37×103)3
∵(103)3=103×103×103=103+3+3=109
∴地球的体积V109
≈10.8×1012(立方千米)
如何计算?
探究新知
(53)2,[(-3)2]3,和(a2)5 各表示什么意思?怎么计算?
①(53)2
=(53)×(53)
= 56
②[(-3)2]3
=(-3)2×(-3)2×(-3)2
= (-3)2+2+2
③ (a2)5
=(a)2×(a)2×(a)2×(a)2×(a)2
= a2+2+2+2+2
= (-3)2×3
= (-3)6
= a2×5
= a10
观察上面算式的计算结果,你发现了什么规律?
幂的乘方的运算性质:
探究新知
根据发现,猜想:(am)n = (m,n都是正整数)
如何说明你的猜想是正确的?
(am)n
= am·am······am·am·am
n个am
= am+m+···+m
n个m
= amn
amn
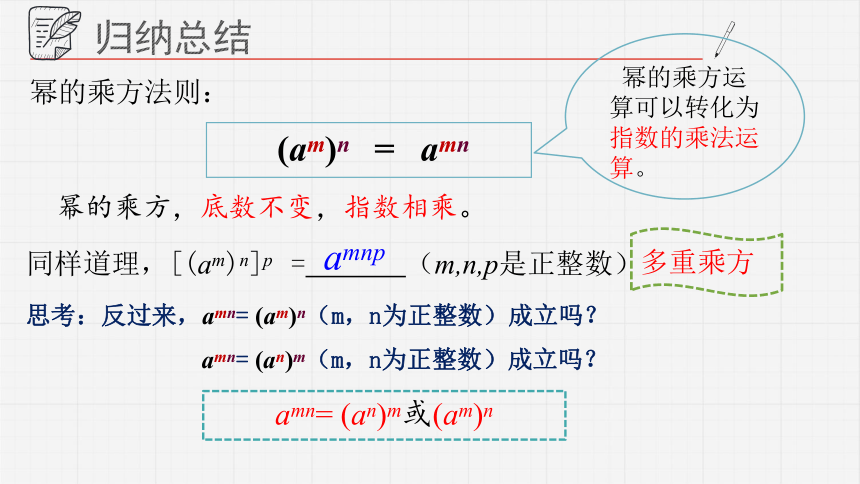
(am)n = amn
幂的乘方,底数不变,指数相乘。
幂的乘方法则:
归纳总结
思考:反过来,amn= (am)n(m,n为正整数)成立吗?
amn= (an)m(m,n为正整数)成立吗?
幂的乘方运算可以转化为指数的乘法运算。
amn= (an)m或(am)n
同样道理,[(am)n]p = (m,n,p是正整数)
amnp
多重乘方
(am)n=amn amn= (an)m或(am)n
逆用
大展身手:已知a3=2,求a6.
探究新知
性质逆用:
解:
∵ a3=2,
∴ a6 =(a3)2
=22
=4
例3、计算:
(1)(-5ab2)3 ; (2)(23)2×(52)3
典型例题
解:
(1)(-5ab2)3 =(-5)3·a3·(b2)3
(2)(23)2×(52)3
= 23×2 ×52×3
= -125a3b6
= 26 ×56
= (2×5)6
= 106
即学即练
1、下列计算对不对?如果不对,应怎样改正?
(1)
(2)
(3)
(4)
×
×
×
×
(x3)2=x6
m3 m6=m9
a4 a4=a8
(t6)4=t24
变式训练
解:
(1)(x3)2 · (x2)2
计算:
(1) (x3)2 · (x2)2; (2) (c2)n·cn+2 ; (3) (-x3)2·x8+(x7)2.
= x6·x4
= x6+4
= x10
(2) (c2)n·cn+2
=c2n·cn+2
= c2n+n+2
= c3n+2
(3)(-x3)2·x8+(x7)2
= x6·x8 + x14
= x14+x14
= 2x14
巩固提升
1、已知a3n=5,b2n=3,求:a6nb4n的值.
=25×9
解:
a6nb4n
=(a3n)2 (b2n)2
=52×32
2、你能比较355,444、533的大小吗?
解:
355
=35×11
=225
=24311
444
=44×11
=24511
533
=53×11
=12511
∵125<243<245
∴ 533<355<444
课堂小结
①幂的乘方的运算性质:
(am)n = amn(m,n为正整数)
即:幂的乘方,底数不变,指数相乘。
amn = (an)m或(am)n (m,n为正整数)
③幂乘方的逆运算:
②多重乘方的运算:
[(am)n]p =amnp(m,n,p是正整数)
课后作业
作业:
P81 练习,习题11.2
同步练习册
11.2.2积的乘方与幂的乘方
七年级下册第十一单元
复习回顾
1、同底数幂的乘法法则
am · an=am+n(m,n都是正整数)
2、积的乘方法则
(ab)n=anbn(n是正整数)
3、积的乘方逆运算
anbn=(ab)n(n是正整数)
1.能说出幂的乘方的运算性质,并会用符号表示;
2.能灵活运用幂的乘方法则进行计算,并能说出每一步运算的依据;
3.熟练运用法则解决问题。
学习目标
学习任务:
1.探索幂的乘方的运算性质
2.幂的乘方等运算性质的运用
=×6.373×(103)3
问题引入
地球可以近似地看做是球体,球的半径约为6.37×103 千米,它的体积大约是多少(精确到1010立方千米)?
提示:球的体积公式为 V= (r表示球的半径)
V= =×(6.37×103)3
∵(103)3=103×103×103=103+3+3=109
∴地球的体积V109
≈10.8×1012(立方千米)
如何计算?
探究新知
(53)2,[(-3)2]3,和(a2)5 各表示什么意思?怎么计算?
①(53)2
=(53)×(53)
= 56
②[(-3)2]3
=(-3)2×(-3)2×(-3)2
= (-3)2+2+2
③ (a2)5
=(a)2×(a)2×(a)2×(a)2×(a)2
= a2+2+2+2+2
= (-3)2×3
= (-3)6
= a2×5
= a10
观察上面算式的计算结果,你发现了什么规律?
幂的乘方的运算性质:
探究新知
根据发现,猜想:(am)n = (m,n都是正整数)
如何说明你的猜想是正确的?
(am)n
= am·am······am·am·am
n个am
= am+m+···+m
n个m
= amn
amn
(am)n = amn
幂的乘方,底数不变,指数相乘。
幂的乘方法则:
归纳总结
思考:反过来,amn= (am)n(m,n为正整数)成立吗?
amn= (an)m(m,n为正整数)成立吗?
幂的乘方运算可以转化为指数的乘法运算。
amn= (an)m或(am)n
同样道理,[(am)n]p = (m,n,p是正整数)
amnp
多重乘方
(am)n=amn amn= (an)m或(am)n
逆用
大展身手:已知a3=2,求a6.
探究新知
性质逆用:
解:
∵ a3=2,
∴ a6 =(a3)2
=22
=4
例3、计算:
(1)(-5ab2)3 ; (2)(23)2×(52)3
典型例题
解:
(1)(-5ab2)3 =(-5)3·a3·(b2)3
(2)(23)2×(52)3
= 23×2 ×52×3
= -125a3b6
= 26 ×56
= (2×5)6
= 106
即学即练
1、下列计算对不对?如果不对,应怎样改正?
(1)
(2)
(3)
(4)
×
×
×
×
(x3)2=x6
m3 m6=m9
a4 a4=a8
(t6)4=t24
变式训练
解:
(1)(x3)2 · (x2)2
计算:
(1) (x3)2 · (x2)2; (2) (c2)n·cn+2 ; (3) (-x3)2·x8+(x7)2.
= x6·x4
= x6+4
= x10
(2) (c2)n·cn+2
=c2n·cn+2
= c2n+n+2
= c3n+2
(3)(-x3)2·x8+(x7)2
= x6·x8 + x14
= x14+x14
= 2x14
巩固提升
1、已知a3n=5,b2n=3,求:a6nb4n的值.
=25×9
解:
a6nb4n
=(a3n)2 (b2n)2
=52×32
2、你能比较355,444、533的大小吗?
解:
355
=35×11
=225
=24311
444
=44×11
=24511
533
=53×11
=12511
∵125<243<245
∴ 533<355<444
课堂小结
①幂的乘方的运算性质:
(am)n = amn(m,n为正整数)
即:幂的乘方,底数不变,指数相乘。
amn = (an)m或(am)n (m,n为正整数)
③幂乘方的逆运算:
②多重乘方的运算:
[(am)n]p =amnp(m,n,p是正整数)
课后作业
作业:
P81 练习,习题11.2
同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
