初中数学青岛版七年级下册11.3.1单项式的乘法课件 16张PPT
文档属性
| 名称 | 初中数学青岛版七年级下册11.3.1单项式的乘法课件 16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
11.3.1 单项式的乘法
七年级下册第十一单元
复习回顾
1.同底数幂的运算法则是:
2.积的乘方的运算法则是:
3.幂的乘方的运算法则是:
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘.
积的乘方等于各因数乘方的积。
am an=am+n(m、n为正整数 )
(am)n=amn(m、n为正整数)
(ab)n=an·bn ( n为正整数)
复习回顾
1.什么是单项式?
由数与字母或字母与字母相乘组成的代数式叫单项式。
单独的一个数或一个字母也是单项式。
2.判断下列哪些是单项式? 它们的系数分别是什么?
8x
a-2a2bc
xy2
3-t2
-10xy2z3
9axy2
1.经历探索单项式相乘的运算性质的过程,明确其算理,发展有条理的思考能力和表达能力。
2.了解单项式相乘的运算性质,并用运算性质进行计算,解决一些实际问题,体会转化思想。
学习目标
学习任务:
1.探索单项式相乘的运算性质
2.单项式相乘运算性质的运用
问题引入
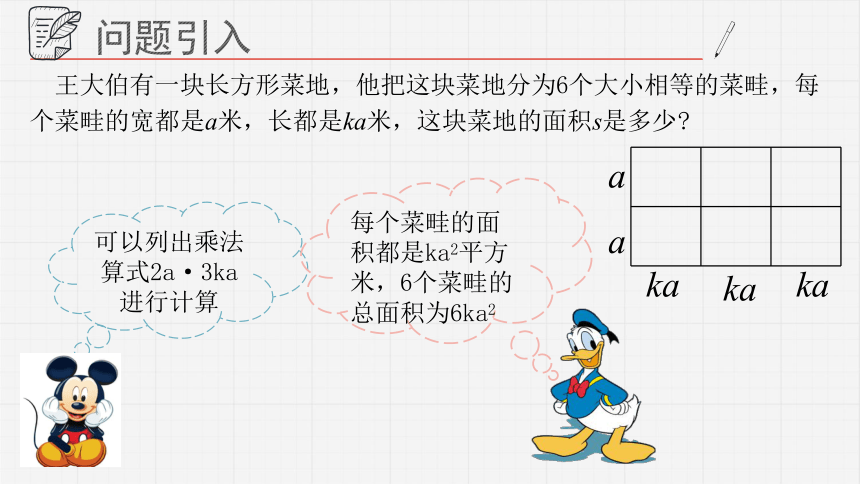
王大伯有一块长方形菜地,他把这块菜地分为6个大小相等的菜畦,每个菜畦的宽都是a米,长都是ka米,这块菜地的面积s是多少
ka
a
a
ka
ka
可以列出乘法算式2a·3ka进行计算
每个菜畦的面积都是ka2平方米,6个菜畦的总面积为6ka2
问题引入
王大伯有一块长方形菜地,他把这块菜地分为6个大小相等的菜畦,每个菜畦的宽都是a米,长都是ka米,这块菜地的面积s是多少
ka
a
a
ka
ka
2a·3ka 6ka2
=
请同学们观察我们得出等式的左右两边有什么特点?
2a·3ka
=(2×3)ka·a
= 6ka2
交流发现
你会计算(-2abc)·(3ab2)吗?
解:原式=[(-2)×3]·(aa)·(bb2)·c
=-6a2b3c
(系数×系数)
(同底数幂相乘)
单独的幂
你能概括单项式相乘的运算性质吗?
单项式相乘,把它们的系数相乘、字母部分的同底数幂分别相乘.对于只在一个单项式中含有的字母,连同它的指数作为积的一个因式。
单项式与单项式相乘的法则:
归纳总结
单项式×单项式
=(系数×系数)·(同底数幂相乘)·(单独的幂)
典型例题
例1: (1)4a3·7a4 (2)7ax·(-2a2bx2)
(1) 4a3·7a4
=(4×7)·(a3·a4)
解:
= 28a7
(2) 7ax·(-2a2bx2)
=[7×(-2)]·(a·a2)·b·(x·x2)
= -14a3bx3
单项式的乘法法则对于三个以上的单项式相乘也适用.
典型例题
例2:求单项式的积。
解:
=
=
即学即练
(1) 4a2 2a4 = 8a8
(2) 6a3 5a2=11a5
(3)(-7a) (-3a3)=-21a4
(4) 3a2b 4a3=12a5
×
×
×
×
4a2 2a4 = 8a6
指数相加
6a3 5a2=30a5
系数相乘
(-7a) (-3a3)=21a4
符号!
3a2b 4a3=12a5b
单独存在的字母,要连同它的指数写在积里!
1、下列计算对不对?如果不对,应怎样改正?
归纳总结
(1)求系数的积,应注意符号;
(2)相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
单项式乘法中要注意的几点:
(3)单独存在的字母,要连同它的指数写在积里,防止遗漏;
(4)单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
(5)单项式乘法的法则对于三个以上的单项式相乘同样适用。
巩固提升
1、计算(-2a2)3 ·(-3a3)2
解:
(-2a2)3 ·(-3a3)2
= -2a6 ·3a6
= -72a12
2、计算:4a2x2·(-3a3bx)3
解:
4a2x2·(-3a3bx)3
= 4a2x2·(-3)3a9b3x3
=[4×(-27)]·(a2·a9)·(x2·x3)·b3
=(-108)a11x5b3
注意:
(1)先乘方,再单项式相乘。
(2)系数相乘不要漏掉负号
= -108a11x5b3
×
= -8a6 ·9a6
拓展延伸
1、卫星绕地球运动的速度(即第一宇宙速度)约为7.9×103米/秒,则卫星运行3×102秒所走的路程约是多少?
解:
=7.9×3×103×102
=23.7×105
7.9×103×3×102
答:.....
=2.37×106
课堂小结
单项式与单项式相乘的法则步骤:
(1)有乘方运算时,先进行乘方运算;
(2)各单项式中的系数相乘;
(3)各单项式中的同底数幂相乘;
(4)单独存在的字母,要连同它的指数一起作为积的一个因式。
(5)单项式乘法的法则对于三个以上的单项式相乘同样适用。
课后作业
作业:
P84 练习
同步练习册
11.3.1 单项式的乘法
七年级下册第十一单元
复习回顾
1.同底数幂的运算法则是:
2.积的乘方的运算法则是:
3.幂的乘方的运算法则是:
同底数幂相乘,底数不变,指数相加.
幂的乘方,底数不变,指数相乘.
积的乘方等于各因数乘方的积。
am an=am+n(m、n为正整数 )
(am)n=amn(m、n为正整数)
(ab)n=an·bn ( n为正整数)
复习回顾
1.什么是单项式?
由数与字母或字母与字母相乘组成的代数式叫单项式。
单独的一个数或一个字母也是单项式。
2.判断下列哪些是单项式? 它们的系数分别是什么?
8x
a-2a2bc
xy2
3-t2
-10xy2z3
9axy2
1.经历探索单项式相乘的运算性质的过程,明确其算理,发展有条理的思考能力和表达能力。
2.了解单项式相乘的运算性质,并用运算性质进行计算,解决一些实际问题,体会转化思想。
学习目标
学习任务:
1.探索单项式相乘的运算性质
2.单项式相乘运算性质的运用
问题引入
王大伯有一块长方形菜地,他把这块菜地分为6个大小相等的菜畦,每个菜畦的宽都是a米,长都是ka米,这块菜地的面积s是多少
ka
a
a
ka
ka
可以列出乘法算式2a·3ka进行计算
每个菜畦的面积都是ka2平方米,6个菜畦的总面积为6ka2
问题引入
王大伯有一块长方形菜地,他把这块菜地分为6个大小相等的菜畦,每个菜畦的宽都是a米,长都是ka米,这块菜地的面积s是多少
ka
a
a
ka
ka
2a·3ka 6ka2
=
请同学们观察我们得出等式的左右两边有什么特点?
2a·3ka
=(2×3)ka·a
= 6ka2
交流发现
你会计算(-2abc)·(3ab2)吗?
解:原式=[(-2)×3]·(aa)·(bb2)·c
=-6a2b3c
(系数×系数)
(同底数幂相乘)
单独的幂
你能概括单项式相乘的运算性质吗?
单项式相乘,把它们的系数相乘、字母部分的同底数幂分别相乘.对于只在一个单项式中含有的字母,连同它的指数作为积的一个因式。
单项式与单项式相乘的法则:
归纳总结
单项式×单项式
=(系数×系数)·(同底数幂相乘)·(单独的幂)
典型例题
例1: (1)4a3·7a4 (2)7ax·(-2a2bx2)
(1) 4a3·7a4
=(4×7)·(a3·a4)
解:
= 28a7
(2) 7ax·(-2a2bx2)
=[7×(-2)]·(a·a2)·b·(x·x2)
= -14a3bx3
单项式的乘法法则对于三个以上的单项式相乘也适用.
典型例题
例2:求单项式的积。
解:
=
=
即学即练
(1) 4a2 2a4 = 8a8
(2) 6a3 5a2=11a5
(3)(-7a) (-3a3)=-21a4
(4) 3a2b 4a3=12a5
×
×
×
×
4a2 2a4 = 8a6
指数相加
6a3 5a2=30a5
系数相乘
(-7a) (-3a3)=21a4
符号!
3a2b 4a3=12a5b
单独存在的字母,要连同它的指数写在积里!
1、下列计算对不对?如果不对,应怎样改正?
归纳总结
(1)求系数的积,应注意符号;
(2)相同字母因式相乘,是同底数幂的乘法,底数不变,指数相加;
单项式乘法中要注意的几点:
(3)单独存在的字母,要连同它的指数写在积里,防止遗漏;
(4)单项式乘以单项式的结果仍然是一个单项式,结果要把系数写在字母因式的前面;
(5)单项式乘法的法则对于三个以上的单项式相乘同样适用。
巩固提升
1、计算(-2a2)3 ·(-3a3)2
解:
(-2a2)3 ·(-3a3)2
= -2a6 ·3a6
= -72a12
2、计算:4a2x2·(-3a3bx)3
解:
4a2x2·(-3a3bx)3
= 4a2x2·(-3)3a9b3x3
=[4×(-27)]·(a2·a9)·(x2·x3)·b3
=(-108)a11x5b3
注意:
(1)先乘方,再单项式相乘。
(2)系数相乘不要漏掉负号
= -108a11x5b3
×
= -8a6 ·9a6
拓展延伸
1、卫星绕地球运动的速度(即第一宇宙速度)约为7.9×103米/秒,则卫星运行3×102秒所走的路程约是多少?
解:
=7.9×3×103×102
=23.7×105
7.9×103×3×102
答:.....
=2.37×106
课堂小结
单项式与单项式相乘的法则步骤:
(1)有乘方运算时,先进行乘方运算;
(2)各单项式中的系数相乘;
(3)各单项式中的同底数幂相乘;
(4)单独存在的字母,要连同它的指数一起作为积的一个因式。
(5)单项式乘法的法则对于三个以上的单项式相乘同样适用。
课后作业
作业:
P84 练习
同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
