初中数学青岛版七年级下册11.1同底数幂的乘法 16张PPT
文档属性
| 名称 | 初中数学青岛版七年级下册11.1同底数幂的乘法 16张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 22:21:59 | ||
图片预览






文档简介
(共16张PPT)
11.1 同底数幂的乘法
七年级下册第十一单元
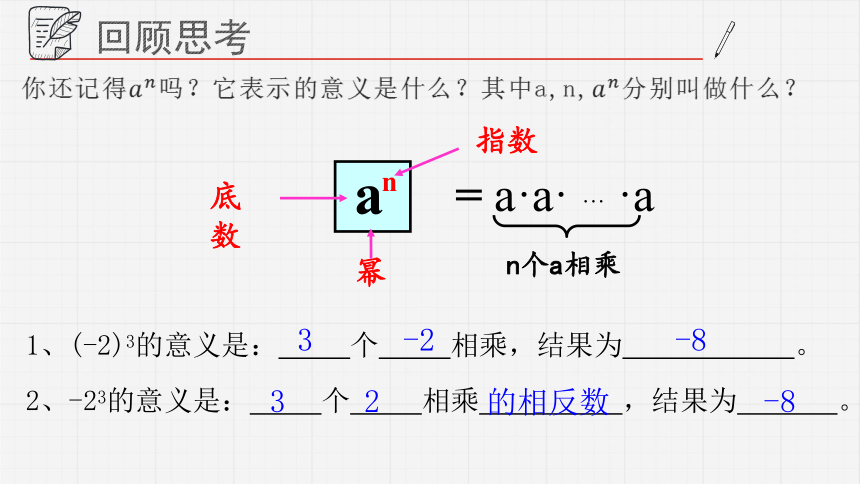
a
n
指数
幂
= a·a· … ·a
n个a相乘
底数
你还记得吗?它表示的意义是什么?其中a,n,分别叫做什么?
回顾思考
1、(-2)3的意义是: 个 相乘,结果为 。
2、-23的意义是: 个 相乘 ,结果为 。
3
-2
-8
3
2
的相反数
-8
1.经历探索同底数幂的乘法的运算性质的过程,进一步体会幂的意义。
2.能通过举例认识同底数幂及同底数幂的乘法。
3.能正确运用同底数幂的乘法运算性质进行计算。
学习目标
重点:理解并掌握同底数幂乘法的运算性质。
难点:运用同底数幂乘法的运算性质进行相关运算。
问题引入
问题:少年宫的小游泳池中存有约100立方米的水。为了保证池水的清洁卫生,必须按规定的比例向池水中加施一定量的消毒剂。为此,需要将水的体积单位转换成升。100立方米的水折合成多少升呢?
提示:1立方米=103升
100立方米=102立方米
100立方米=10 ×10 升
100立方米=10 ×10 升
同底数幂相乘
请你根据乘方的意义计算10 ×10
10 ×10 =(10×10)×(10×10×10)
所以游泳池里大约有水105升。
=10×10×10×10×10
交流发现
=105
请同学们仿照上面的方法,计算下列各式。
合作探究
2
3、a ·a
=(-2)×(-2)×(-2)×(-2)×(-2)×(-2)×(-2)×(-2)×(-2)
=(-2)9
1、(-2)3×(-2)6
=()×()×()×()×()×()×()×()×()
=()9
=a·a·a·a·a
=a5
4、7m×7n
=7×7×7×7···×7×7×7×7····×7
m个7相乘
n个7相乘
=7m+n
观察上面各题左右两边,底数、指数有什么关系?
同底数幂的乘法法则:
探究新知
根据发现,猜想:am an= (m,n都是正整数)
am+n
如何说明你的猜想是正确的?
am an
=(a·a·a····a)·(a·a·a····a·a)
m个a
n个a
=a·a·a····a·a·a·a
m+n个a
=am+n
(乘方的意义)
(乘法结合律)
底数相同的幂叫做同底数幂。
它们的乘法叫做同底数幂的乘法。
同底数幂的乘法法则:
归纳总结
am an=am+n(m,n都为正整数)
同底数幂相乘,底数不变,指数相加。
注意
(1)运算形式(同底、乘法)
(2)运算方法(底不变,指相加)
同底数幂的乘法运算可以转化为指数的加法运算。
同样道理,am·an·ap= (m、n、p都是正整数)
am+n+p
即学即练
1、下列计算对不对?如果不对,应怎样改正?
(1)
(2)
(3)
(4)
×
×
×
×
例1、计算:
(1)32×35 ; (2)( 5)3×( 5)5.
典型例题
解:
(1)32×35 = 32+5 = 37
(2)( 5)3×( 5)5 =( 5)3+5 =( 5)8
变式训练:
(1)()2×()5
(2)(-3)5×(-3)8
(3)x4×(-x)3
= 58
典型例题
例2、计算:
(1)a8·a3·a; (2)(a+b)2·(a+b)3.
解:
(1)a8·a3·a = a8+3+1 = a12
(2)(a+b)2·(a+b)3=(a+b)2+3=(a+b)5
变式训练:
(1)b2·b6·b5
(2)(a-b)3·(a-b)·(a-b)2
例3、某台电脑每秒可作1015次运算,它工作5小时,可作多少次运算?
典型例题
解:
5×3600=5×3.6×103=1.8×10×103
所以,5小时等于1.8×104秒
1015×(1.8×104)
=1.8×(104×1015)
=1.8×1019.
所以,该电脑工作5小时可作1.8×1019次的运算。
=1.8×104.
巩固提升
光的传播速度约为3×105千米/秒,太阳光照射到地球上大约需要经过5×102秒,地球离太阳大约多少千米(用科学计数法表示)?
点拨:路程=速度×时间
解:由题意得
3×105 × 5×102
=1.5×108(千米)
答:地球离太阳大约1.5×108千米.
拓展延伸
1、若xm+1·xm-2=x3,试求出m2的值。
解:
∴ xm+1+m-2=x3
∴ m+1+m-2=3
∴ m=2
∴ m2=4
∵ xm+1·xm-2=x3
2、若xa=3,xb=5,求xa+b的值。
解:
xa+b = xa·xb
=3×5
=15
∴xa+b=15
课堂小结
am an=am+n(m,n都为正整数)
同底数幂相乘,底数不变,指数相加。
注意
(1)运算形式(同底、乘法)
(2)运算方法(底不变,指相加)
课后作业
作业:
P77 练习
P78 习题11.1 同步练习册
11.1 同底数幂的乘法
七年级下册第十一单元
a
n
指数
幂
= a·a· … ·a
n个a相乘
底数
你还记得吗?它表示的意义是什么?其中a,n,分别叫做什么?
回顾思考
1、(-2)3的意义是: 个 相乘,结果为 。
2、-23的意义是: 个 相乘 ,结果为 。
3
-2
-8
3
2
的相反数
-8
1.经历探索同底数幂的乘法的运算性质的过程,进一步体会幂的意义。
2.能通过举例认识同底数幂及同底数幂的乘法。
3.能正确运用同底数幂的乘法运算性质进行计算。
学习目标
重点:理解并掌握同底数幂乘法的运算性质。
难点:运用同底数幂乘法的运算性质进行相关运算。
问题引入
问题:少年宫的小游泳池中存有约100立方米的水。为了保证池水的清洁卫生,必须按规定的比例向池水中加施一定量的消毒剂。为此,需要将水的体积单位转换成升。100立方米的水折合成多少升呢?
提示:1立方米=103升
100立方米=102立方米
100立方米=10 ×10 升
100立方米=10 ×10 升
同底数幂相乘
请你根据乘方的意义计算10 ×10
10 ×10 =(10×10)×(10×10×10)
所以游泳池里大约有水105升。
=10×10×10×10×10
交流发现
=105
请同学们仿照上面的方法,计算下列各式。
合作探究
2
3、a ·a
=(-2)×(-2)×(-2)×(-2)×(-2)×(-2)×(-2)×(-2)×(-2)
=(-2)9
1、(-2)3×(-2)6
=()×()×()×()×()×()×()×()×()
=()9
=a·a·a·a·a
=a5
4、7m×7n
=7×7×7×7···×7×7×7×7····×7
m个7相乘
n个7相乘
=7m+n
观察上面各题左右两边,底数、指数有什么关系?
同底数幂的乘法法则:
探究新知
根据发现,猜想:am an= (m,n都是正整数)
am+n
如何说明你的猜想是正确的?
am an
=(a·a·a····a)·(a·a·a····a·a)
m个a
n个a
=a·a·a····a·a·a·a
m+n个a
=am+n
(乘方的意义)
(乘法结合律)
底数相同的幂叫做同底数幂。
它们的乘法叫做同底数幂的乘法。
同底数幂的乘法法则:
归纳总结
am an=am+n(m,n都为正整数)
同底数幂相乘,底数不变,指数相加。
注意
(1)运算形式(同底、乘法)
(2)运算方法(底不变,指相加)
同底数幂的乘法运算可以转化为指数的加法运算。
同样道理,am·an·ap= (m、n、p都是正整数)
am+n+p
即学即练
1、下列计算对不对?如果不对,应怎样改正?
(1)
(2)
(3)
(4)
×
×
×
×
例1、计算:
(1)32×35 ; (2)( 5)3×( 5)5.
典型例题
解:
(1)32×35 = 32+5 = 37
(2)( 5)3×( 5)5 =( 5)3+5 =( 5)8
变式训练:
(1)()2×()5
(2)(-3)5×(-3)8
(3)x4×(-x)3
= 58
典型例题
例2、计算:
(1)a8·a3·a; (2)(a+b)2·(a+b)3.
解:
(1)a8·a3·a = a8+3+1 = a12
(2)(a+b)2·(a+b)3=(a+b)2+3=(a+b)5
变式训练:
(1)b2·b6·b5
(2)(a-b)3·(a-b)·(a-b)2
例3、某台电脑每秒可作1015次运算,它工作5小时,可作多少次运算?
典型例题
解:
5×3600=5×3.6×103=1.8×10×103
所以,5小时等于1.8×104秒
1015×(1.8×104)
=1.8×(104×1015)
=1.8×1019.
所以,该电脑工作5小时可作1.8×1019次的运算。
=1.8×104.
巩固提升
光的传播速度约为3×105千米/秒,太阳光照射到地球上大约需要经过5×102秒,地球离太阳大约多少千米(用科学计数法表示)?
点拨:路程=速度×时间
解:由题意得
3×105 × 5×102
=1.5×108(千米)
答:地球离太阳大约1.5×108千米.
拓展延伸
1、若xm+1·xm-2=x3,试求出m2的值。
解:
∴ xm+1+m-2=x3
∴ m+1+m-2=3
∴ m=2
∴ m2=4
∵ xm+1·xm-2=x3
2、若xa=3,xb=5,求xa+b的值。
解:
xa+b = xa·xb
=3×5
=15
∴xa+b=15
课堂小结
am an=am+n(m,n都为正整数)
同底数幂相乘,底数不变,指数相加。
注意
(1)运算形式(同底、乘法)
(2)运算方法(底不变,指相加)
课后作业
作业:
P77 练习
P78 习题11.1 同步练习册
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
