8.5 乘法公式 第1课时 课件 2023-2024学年初中数学冀教版七年级下册(共16张PPT)
文档属性
| 名称 | 8.5 乘法公式 第1课时 课件 2023-2024学年初中数学冀教版七年级下册(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 892.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 23:09:03 | ||
图片预览






文档简介
(共16张PPT)
第八章 整式的乘法
8.5 乘法公式
第1课时
一、学习目标
1.能用多项式乘法推导平方差公式,会用图形的面积割补说明
平方差公式;
2.掌握平方差公式的结构特征,能运用公式进行计算;(重点)
3.会用乘法公式简化运算.
二、新课导入
复习引入
多项式与多项式相乘,先用一个多项式的 乘另一个多项式
的 ,再把所得的积相加.
每一项
每一项
多项式与多项式是如何相乘的?
(a+b)(m+n)=
am
an
bm
bn
+
+
+
三、自主学习
知识点 平方差公式
自主探究
(x+1)(x-1) = .
(a+2)(a-2) = .
(2x+1)(2x-1) = .
x2-1
a2-4
4x2-1
计算:
猜想:
(a+b)(a-b)= .
a2-b2
三、自主学习
验证1:
(a+b)(a-b)
=a2-ab .
=a2- .
思考:你还能用图形面积的方式去验证这个公式吗?
(多项式乘多项式的法则)
(合并同类项)
+ab-b2
b2
三、自主学习
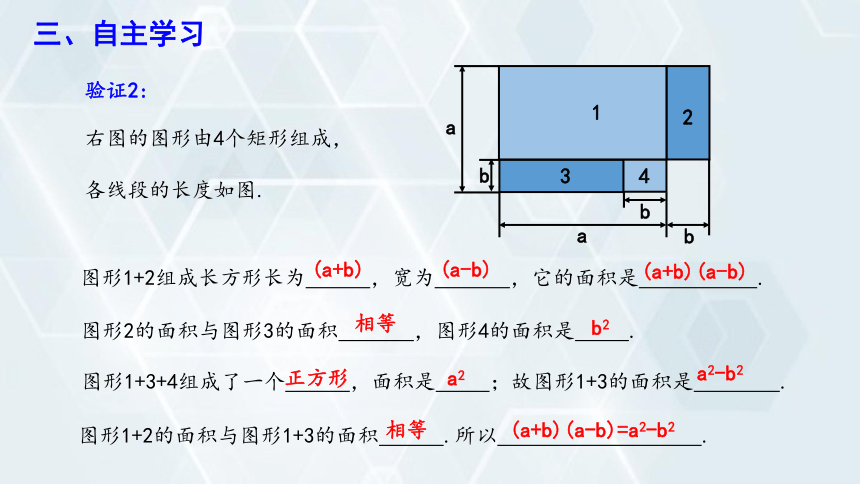
验证2:
3
4
1
2
a
a
b
b
b
图形1+2组成长方形长为 ,宽为 ,它的面积是 .
图形2的面积与图形3的面积 ,图形4的面积是 .
图形1+3+4组成了一个 ,面积是 ;故图形1+3的面积是 .
图形1+2的面积与图形1+3的面积 .所以 .
相等
相等
(a+b)(a-b)=a2-b2
右图的图形由4个矩形组成,
各线段的长度如图.
(a+b)
(a-b)
(a+b)(a-b)
b2
正方形
a2
a2-b2
三、自主学习
要点归纳
平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差.
(a+b)(a-b)=a2-b2
公式变形
1.(a-b)(a+b)=a2-b2.
2.(b+a)(-b+a)=a2-b2.
如何用语言描述?
四、合作探究
探究一 直接利用平方差公式进行计算
问题提出:如何利用平方差公式计算(-x-3)(3-x)?
问题探究:我们已经知道平方差公式(a+b)(a-b)=a2-b2,在两个多项式相乘
(a+b)(a-b)中,a同号,b .
利用以上区分方法,在(-x-3)(3-x)中,对应a的是 ,对应b的是 .
故我们利用平方差公式将式子(-x-3)(3-x)转为( )2 - ( )2.
问题解决:
解:原式= = .
应用:一辆汽车以(3-x)km/h的速度行驶了(-x-3)小时,行驶路程为 km.
异号
-x
3
-x
3
(-x)2 - 32
x2 - 9
x2 -9
四、合作探究
总结:利用平方差公式计算时:
1.先把要计算的式子与公式对照;
2.分清哪个是a 哪个是b (a同号,b异号);
3.套用公式计算.
四、合作探究
练一练
1.计算:(1) (3x+4)(3x-4) (2)(3a-4b)(-4b-3a)
解:
原式=(3x)2-42
=9x2-16
原式=(-4b+3a)(-4b-3a)
=(-4b)2-(3a)2
=16b2-3a2
(3) (y+2)(y-2)–(y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1
注意:在(3)式中(y-1)(y+5)不是(a+b)(a-b)
的形式,所以不能利用平方差公式计算;
多组运算再相加减,结果要合并同类项.
四、合作探究
探究2 巧用平方差公式简便计算
问题提出:如何利用平方差公式简便计算102×98?
问题探究:如果要利用平方差公式简便计算,那么一定要将102×98
转化为 的形式,并且a2和b2都要计算方便;
问题解决:
解:原式= = = .
应用:直接写出答案:103×97= .
(a+b)(a-b)
根据以上提示,102×98可转化为( + )( - )
100
100
2
2
(100+2)(100-2)
1002-22
9996
9991
四、合作探究
练一练
2.用便捷的方式计算:49×51-4×252
解:原式=(50-1)(50+1)-22×252
=502-12-(2×25)2
=502-1-502
=-1
五、当堂检测
1.利用平方差公式计算:
(1)(2a+5b)(2a-5b)
解:
(2)( x-3)( x+3);
(3)(y-2x)(-2x-y);
(4)(xy+1)(xy-1);
原式=(2a)2 -(5b)2
=4a2 -25b2
原式=( x)2 -32
= x2 -9
原式=(-2x)2 -y2
=4x2 -y2
原式=(xy)2 -1
=x2y2 -1
五、当堂检测
2.利用乘法公式计算:
(1)39.8×40.2
(2)992
原式=(40-0.2)(40+0.2)
=402-0.22
=1600-0.04
=1599.96
原式=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801
五、当堂检测
3.解下列方程:
(1)4x2+x-(2x-3)(2x+3)=1
(2)2(x+3)(3-x)+2x+2x2=20
解:4x2+x-(2x-3)(2x+3)=1
4x2+x-(4x2-9)=1
4x2+x-4x2+9=1
x=-8
解:2(x+3)(3-x)+2x+2x2=20
2(9-x2)+2x+2x2=20
18-2x2+2x+2x2=20
2x=2
x=1
六、课堂总结
平方差公式
符号表示
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
1.紧紧抓住 “一同一反”这一特征
2.对于不能直接应用公式的,可能要
经过变形才可以应用
注意
文字描述
第八章 整式的乘法
8.5 乘法公式
第1课时
一、学习目标
1.能用多项式乘法推导平方差公式,会用图形的面积割补说明
平方差公式;
2.掌握平方差公式的结构特征,能运用公式进行计算;(重点)
3.会用乘法公式简化运算.
二、新课导入
复习引入
多项式与多项式相乘,先用一个多项式的 乘另一个多项式
的 ,再把所得的积相加.
每一项
每一项
多项式与多项式是如何相乘的?
(a+b)(m+n)=
am
an
bm
bn
+
+
+
三、自主学习
知识点 平方差公式
自主探究
(x+1)(x-1) = .
(a+2)(a-2) = .
(2x+1)(2x-1) = .
x2-1
a2-4
4x2-1
计算:
猜想:
(a+b)(a-b)= .
a2-b2
三、自主学习
验证1:
(a+b)(a-b)
=a2-ab .
=a2- .
思考:你还能用图形面积的方式去验证这个公式吗?
(多项式乘多项式的法则)
(合并同类项)
+ab-b2
b2
三、自主学习
验证2:
3
4
1
2
a
a
b
b
b
图形1+2组成长方形长为 ,宽为 ,它的面积是 .
图形2的面积与图形3的面积 ,图形4的面积是 .
图形1+3+4组成了一个 ,面积是 ;故图形1+3的面积是 .
图形1+2的面积与图形1+3的面积 .所以 .
相等
相等
(a+b)(a-b)=a2-b2
右图的图形由4个矩形组成,
各线段的长度如图.
(a+b)
(a-b)
(a+b)(a-b)
b2
正方形
a2
a2-b2
三、自主学习
要点归纳
平方差公式
两个数的和与这两个数的差的积,等于这两个数的平方差.
(a+b)(a-b)=a2-b2
公式变形
1.(a-b)(a+b)=a2-b2.
2.(b+a)(-b+a)=a2-b2.
如何用语言描述?
四、合作探究
探究一 直接利用平方差公式进行计算
问题提出:如何利用平方差公式计算(-x-3)(3-x)?
问题探究:我们已经知道平方差公式(a+b)(a-b)=a2-b2,在两个多项式相乘
(a+b)(a-b)中,a同号,b .
利用以上区分方法,在(-x-3)(3-x)中,对应a的是 ,对应b的是 .
故我们利用平方差公式将式子(-x-3)(3-x)转为( )2 - ( )2.
问题解决:
解:原式= = .
应用:一辆汽车以(3-x)km/h的速度行驶了(-x-3)小时,行驶路程为 km.
异号
-x
3
-x
3
(-x)2 - 32
x2 - 9
x2 -9
四、合作探究
总结:利用平方差公式计算时:
1.先把要计算的式子与公式对照;
2.分清哪个是a 哪个是b (a同号,b异号);
3.套用公式计算.
四、合作探究
练一练
1.计算:(1) (3x+4)(3x-4) (2)(3a-4b)(-4b-3a)
解:
原式=(3x)2-42
=9x2-16
原式=(-4b+3a)(-4b-3a)
=(-4b)2-(3a)2
=16b2-3a2
(3) (y+2)(y-2)–(y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1
注意:在(3)式中(y-1)(y+5)不是(a+b)(a-b)
的形式,所以不能利用平方差公式计算;
多组运算再相加减,结果要合并同类项.
四、合作探究
探究2 巧用平方差公式简便计算
问题提出:如何利用平方差公式简便计算102×98?
问题探究:如果要利用平方差公式简便计算,那么一定要将102×98
转化为 的形式,并且a2和b2都要计算方便;
问题解决:
解:原式= = = .
应用:直接写出答案:103×97= .
(a+b)(a-b)
根据以上提示,102×98可转化为( + )( - )
100
100
2
2
(100+2)(100-2)
1002-22
9996
9991
四、合作探究
练一练
2.用便捷的方式计算:49×51-4×252
解:原式=(50-1)(50+1)-22×252
=502-12-(2×25)2
=502-1-502
=-1
五、当堂检测
1.利用平方差公式计算:
(1)(2a+5b)(2a-5b)
解:
(2)( x-3)( x+3);
(3)(y-2x)(-2x-y);
(4)(xy+1)(xy-1);
原式=(2a)2 -(5b)2
=4a2 -25b2
原式=( x)2 -32
= x2 -9
原式=(-2x)2 -y2
=4x2 -y2
原式=(xy)2 -1
=x2y2 -1
五、当堂检测
2.利用乘法公式计算:
(1)39.8×40.2
(2)992
原式=(40-0.2)(40+0.2)
=402-0.22
=1600-0.04
=1599.96
原式=(100-1)2
=1002-2×100×1+12
=10000-200+1
=9801
五、当堂检测
3.解下列方程:
(1)4x2+x-(2x-3)(2x+3)=1
(2)2(x+3)(3-x)+2x+2x2=20
解:4x2+x-(2x-3)(2x+3)=1
4x2+x-(4x2-9)=1
4x2+x-4x2+9=1
x=-8
解:2(x+3)(3-x)+2x+2x2=20
2(9-x2)+2x+2x2=20
18-2x2+2x+2x2=20
2x=2
x=1
六、课堂总结
平方差公式
符号表示
两个数的和与这两个数的差的积,等于这两个数的平方差
(a+b)(a-b)=a2-b2
1.紧紧抓住 “一同一反”这一特征
2.对于不能直接应用公式的,可能要
经过变形才可以应用
注意
文字描述
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
