8.5 乘法公式 第2课时 课件 2023-2024学年初中数学冀教版七年级下册(共20张PPT)
文档属性
| 名称 | 8.5 乘法公式 第2课时 课件 2023-2024学年初中数学冀教版七年级下册(共20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 23:14:24 | ||
图片预览





文档简介
(共20张PPT)
第八章 整式的乘法
8.5 乘法公式
第2课时
一、学习目标
2.能够运用完全平方公式进行整式乘法的运算.(重点)
1.通过探索完全平方公式的计算规律,理解并掌握完全平方公式;
二、新课导入
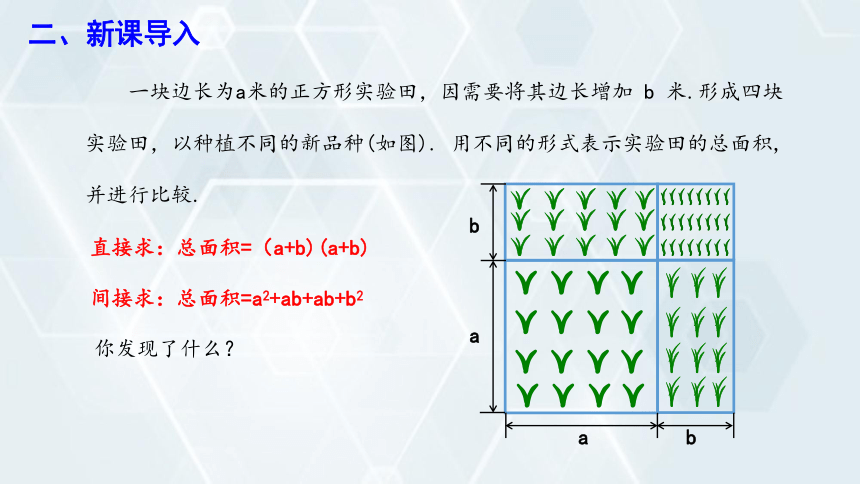
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块
实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积,
并进行比较.
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
b
b
a
a
三、自主学习
知识点一 完全平方公式
自主探究
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
猜想:
三、自主学习
验证:
(a+b)2
=a2+ab .
= .
(多项式乘多项式的法则)
(合并同类项)
+ab+b2
a2+2ab+b2
=(a+b)(a+b)
(a-b)2
= .
= .
(多项式乘多项式的法则)
(合并同类项)
a2-ab-ab+b2
a2-2ab+b2
=(a-b)(a-b)
三、自主学习
要点归纳
完全平方公式
两数和(或差)的平方,等于它们的平方和,
加上(或减去)它们的积的2倍.
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
公式特征
简记为:
“首平方,尾平方,
积的2倍放中间”
4.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,且与乘式中间的符号相同;
三、自主学习
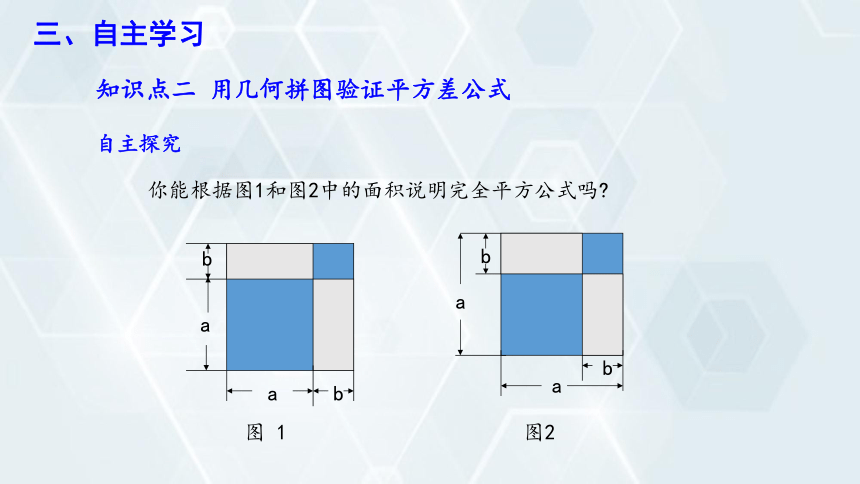
知识点二 用几何拼图验证平方差公式
自主探究
你能根据图1和图2中的面积说明完全平方公式吗
b
a
a
b
b
a
b
a
图 1
图2
三、自主学习
b
a
a
b
a2
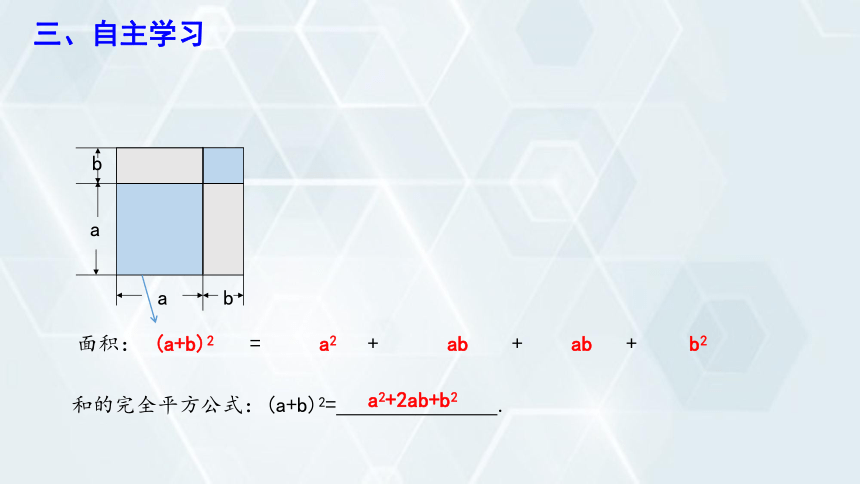
面积:
ab
ab
b2
(a+b)2
+
+
+
=
和的完全平方公式:(a+b)2= .
a2+2ab+b2
三、自主学习
b
a
a
b
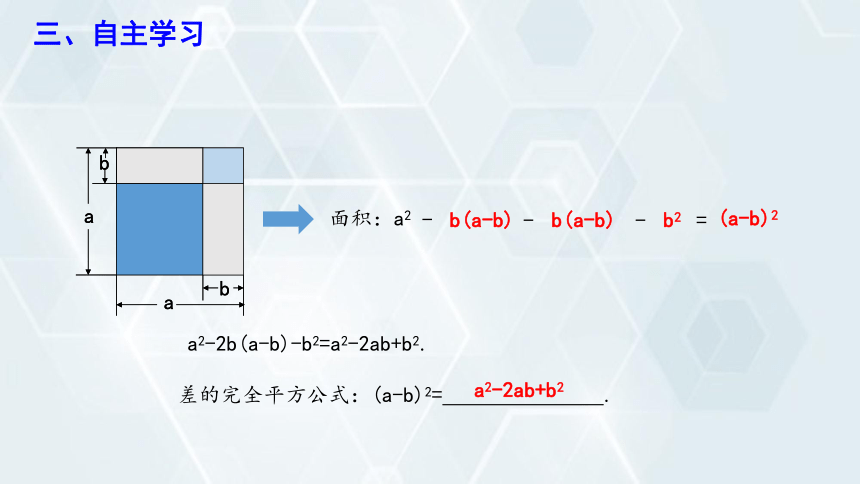
面积:a2
-
-
-
b(a-b)
b2
=
(a-b)2
b
a
a
b
差的完全平方公式:(a-b)2= .
a2-2ab+b2
b(a-b)
a2-2b(a-b)-b2=a2-2ab+b2.
四、合作探究
探究一 利用完全平方公式计算
问题提出:如何利用完全平方公式计算(2m+n)2和(-a-2)2.
问题探究:我们已经知道完全平方公式(a±b)2=a2±2ab+b2,
在(2m+n)2中,与公式中a对应的项是 ,与公式中b对应的项是 .故
原式=( )2+2·2m· +n2,
根据相反数的平方相等,可得(-a-2)2=( )2.
故(-a-2)2=(a+2)2=a2+ ×a+4.
问题解决:
(2m+n)2= = .
(-a-2)2= = = .
2m
n
2m
n
a+2
4
(2m)2+2·2m·n+n2
4m2+4mn+n2
(a+2)2
a2+2·a·2+22
a2+4a+4
四、合作探究
总结:利用完全平方公式计算时,先对照公式分清a和b,再套用公式写
出结果;这里要注意结果是有三项,不要遗漏; 公式结果的第二项+2ab
和-2ab正负号不要弄错以及系数2不要忘乘.
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
由于互为相反数的两个数平方相等,故(-a-b)2=(a+b)2,(b-a)2=(a-b)2.
四、合作探究
练一练
1.运用完全平方公式计算:
(1)(3x+y)2;
(2)(3y-4)2;
原式=(3x)2+2·(3x)·y+y2
解:
=9x2+6xy+y2
原式=(3y)2 -2·(3y)·4+42
=9y2 -24y+16
四、合作探究
探究二 利用完全平方公式简便运算
材料:公元前224年,秦王嬴政召集群臣,商议灭楚大计,王翦认为“非六
十万人不可”,而李信则认为“不过二十万人”便可打败楚国,秦王大喜,
认为王翦老不堪用,便派李信和蒙恬率军二十万,南下伐楚,结果落得惨败.所以秦王只能答应的王翦要求了.
由于60万可是当时秦国所有兵力的总和了,秦王又气又无奈,于是想刁难
一下王翦;他调集了全国的兵力,分为60个正方形方阵:
30个101×101阵,30个99×99方阵(如下图);请王翦清点.
四、合作探究
99人
99人
101人
101人
问题提出:你能帮王翦数下每种方阵的人数吗?你能判断出总人数有没有60万吗?
问题探究:一个99×99方阵的人数为( )2,一个101×101方阵的人数为( )2.
要利用完全平方公式简便计算992和1002,需要将它们转化成 的形式.
(a±b)2
992=( - )2; 1012=( + )2
99
1
100
101
1
100
四、合作探究
接下来就可以利用完全平方公式计算:
992=(100-1)2=10000- +1= ;
1012=(100+1)2=10000+ +1= .
问题解决:一个99×99方阵人数为 ,一个101×101方阵人数为 ;
总人数 (填“超过”或“不超过”)60万.
60个方阵的总人数为:
200
200
9801
12001
30×9801+30×12001=30×(9801+12001)
=30×20002
=600 060
9801
12001
超过
四、合作探究
练一练
1.运用完全平方公式简便运算:
(1)982 (2)2012
=10000-400+4
解:(1)原式
(2)原式
=40000+400+1
=(200+1)2
=40401
=(100-2)2
=9604
五、当堂检测
1.利用乘法公式计算:
(4)(a+b+c)2 ;
(2)(2x+ )2 ;
(1)(-2x+3y)2 .
解:
(4)原式=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
(3)原式=(2x)2+2·(2x) +( )2
=4x2 + 2xy + .
(1)原式=(-2x)2+2(-2x)(3y)+(3y)2
=4x2 - 12xy + 9y2.
=a2+b2+c2+2ab+2bc+2ac.
(3)(x+5)2 -(x-5)2 ;
(3)原式=x2+10x+25-(x2-10x+25)
=x2+10x+25-x2+10x-25
=20x.
五、当堂检测
2.运用完全平方公式简便运算:
(1)8982 (2)1022-400
=(900-2)2
解:(1)原式
(2)原式
=(100+2)2-400
=810000-3600+4
=806404
=10000+400+4-400
=10004
3
五、当堂检测
3.如图,一个正方形,如果边长都增加3 m,它的面积就增加39 m2,求这个正方形的原边长.
3
(单位:m)
解:
设原正方形的边长为x m.
由题意可得(x+3)2-x2=39
[x2+6x+9]-x2=39
6x+9=39
x=5
故原正方形的边长为5 m.
六、课堂总结
完全平方公式
语言描述
(a±b)2= a2 ±2ab+b2
两数的和(或差)的平方,等于
这它们的平方和,加上(或减去)
它们的积的2倍.
符号描述
第八章 整式的乘法
8.5 乘法公式
第2课时
一、学习目标
2.能够运用完全平方公式进行整式乘法的运算.(重点)
1.通过探索完全平方公式的计算规律,理解并掌握完全平方公式;
二、新课导入
一块边长为a米的正方形实验田,因需要将其边长增加 b 米.形成四块
实验田,以种植不同的新品种(如图). 用不同的形式表示实验田的总面积,
并进行比较.
直接求:总面积=(a+b)(a+b)
间接求:总面积=a2+ab+ab+b2
你发现了什么?
b
b
a
a
三、自主学习
知识点一 完全平方公式
自主探究
计算下列多项式的积,你能发现什么规律?
(1) (p+1)2=(p+1)(p+1)= .
p2+2p+1
(2) (m+2)2=(m+2)(m+2)= .
m2+4m+4
(3) (p-1)2=(p-1)(p-1)= .
p2-2p+1
(4) (m-2)2=(m-2)(m-2)= .
m2-4m+4
(a+b)2= .
a2+2ab+b2
(a-b)2= .
a2-2ab+b2
猜想:
三、自主学习
验证:
(a+b)2
=a2+ab .
= .
(多项式乘多项式的法则)
(合并同类项)
+ab+b2
a2+2ab+b2
=(a+b)(a+b)
(a-b)2
= .
= .
(多项式乘多项式的法则)
(合并同类项)
a2-ab-ab+b2
a2-2ab+b2
=(a-b)(a-b)
三、自主学习
要点归纳
完全平方公式
两数和(或差)的平方,等于它们的平方和,
加上(或减去)它们的积的2倍.
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
公式特征
简记为:
“首平方,尾平方,
积的2倍放中间”
4.公式中的字母a,b可以表示数,单项式和多项式.
1.积为二次三项式;
2.积中两项为两数的平方和;
3.另一项是两数积的2倍,且与乘式中间的符号相同;
三、自主学习
知识点二 用几何拼图验证平方差公式
自主探究
你能根据图1和图2中的面积说明完全平方公式吗
b
a
a
b
b
a
b
a
图 1
图2
三、自主学习
b
a
a
b
a2
面积:
ab
ab
b2
(a+b)2
+
+
+
=
和的完全平方公式:(a+b)2= .
a2+2ab+b2
三、自主学习
b
a
a
b
面积:a2
-
-
-
b(a-b)
b2
=
(a-b)2
b
a
a
b
差的完全平方公式:(a-b)2= .
a2-2ab+b2
b(a-b)
a2-2b(a-b)-b2=a2-2ab+b2.
四、合作探究
探究一 利用完全平方公式计算
问题提出:如何利用完全平方公式计算(2m+n)2和(-a-2)2.
问题探究:我们已经知道完全平方公式(a±b)2=a2±2ab+b2,
在(2m+n)2中,与公式中a对应的项是 ,与公式中b对应的项是 .故
原式=( )2+2·2m· +n2,
根据相反数的平方相等,可得(-a-2)2=( )2.
故(-a-2)2=(a+2)2=a2+ ×a+4.
问题解决:
(2m+n)2= = .
(-a-2)2= = = .
2m
n
2m
n
a+2
4
(2m)2+2·2m·n+n2
4m2+4mn+n2
(a+2)2
a2+2·a·2+22
a2+4a+4
四、合作探究
总结:利用完全平方公式计算时,先对照公式分清a和b,再套用公式写
出结果;这里要注意结果是有三项,不要遗漏; 公式结果的第二项+2ab
和-2ab正负号不要弄错以及系数2不要忘乘.
(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
由于互为相反数的两个数平方相等,故(-a-b)2=(a+b)2,(b-a)2=(a-b)2.
四、合作探究
练一练
1.运用完全平方公式计算:
(1)(3x+y)2;
(2)(3y-4)2;
原式=(3x)2+2·(3x)·y+y2
解:
=9x2+6xy+y2
原式=(3y)2 -2·(3y)·4+42
=9y2 -24y+16
四、合作探究
探究二 利用完全平方公式简便运算
材料:公元前224年,秦王嬴政召集群臣,商议灭楚大计,王翦认为“非六
十万人不可”,而李信则认为“不过二十万人”便可打败楚国,秦王大喜,
认为王翦老不堪用,便派李信和蒙恬率军二十万,南下伐楚,结果落得惨败.所以秦王只能答应的王翦要求了.
由于60万可是当时秦国所有兵力的总和了,秦王又气又无奈,于是想刁难
一下王翦;他调集了全国的兵力,分为60个正方形方阵:
30个101×101阵,30个99×99方阵(如下图);请王翦清点.
四、合作探究
99人
99人
101人
101人
问题提出:你能帮王翦数下每种方阵的人数吗?你能判断出总人数有没有60万吗?
问题探究:一个99×99方阵的人数为( )2,一个101×101方阵的人数为( )2.
要利用完全平方公式简便计算992和1002,需要将它们转化成 的形式.
(a±b)2
992=( - )2; 1012=( + )2
99
1
100
101
1
100
四、合作探究
接下来就可以利用完全平方公式计算:
992=(100-1)2=10000- +1= ;
1012=(100+1)2=10000+ +1= .
问题解决:一个99×99方阵人数为 ,一个101×101方阵人数为 ;
总人数 (填“超过”或“不超过”)60万.
60个方阵的总人数为:
200
200
9801
12001
30×9801+30×12001=30×(9801+12001)
=30×20002
=600 060
9801
12001
超过
四、合作探究
练一练
1.运用完全平方公式简便运算:
(1)982 (2)2012
=10000-400+4
解:(1)原式
(2)原式
=40000+400+1
=(200+1)2
=40401
=(100-2)2
=9604
五、当堂检测
1.利用乘法公式计算:
(4)(a+b+c)2 ;
(2)(2x+ )2 ;
(1)(-2x+3y)2 .
解:
(4)原式=[(a+b)+c]2
=(a+b)2+2(a+b)c+c2
(3)原式=(2x)2+2·(2x) +( )2
=4x2 + 2xy + .
(1)原式=(-2x)2+2(-2x)(3y)+(3y)2
=4x2 - 12xy + 9y2.
=a2+b2+c2+2ab+2bc+2ac.
(3)(x+5)2 -(x-5)2 ;
(3)原式=x2+10x+25-(x2-10x+25)
=x2+10x+25-x2+10x-25
=20x.
五、当堂检测
2.运用完全平方公式简便运算:
(1)8982 (2)1022-400
=(900-2)2
解:(1)原式
(2)原式
=(100+2)2-400
=810000-3600+4
=806404
=10000+400+4-400
=10004
3
五、当堂检测
3.如图,一个正方形,如果边长都增加3 m,它的面积就增加39 m2,求这个正方形的原边长.
3
(单位:m)
解:
设原正方形的边长为x m.
由题意可得(x+3)2-x2=39
[x2+6x+9]-x2=39
6x+9=39
x=5
故原正方形的边长为5 m.
六、课堂总结
完全平方公式
语言描述
(a±b)2= a2 ±2ab+b2
两数的和(或差)的平方,等于
这它们的平方和,加上(或减去)
它们的积的2倍.
符号描述
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
