9.2 三角形的内角和外角 第2课时 课件 2023-2024学年初中数学冀教版七年级下册(共21张PPT)
文档属性
| 名称 | 9.2 三角形的内角和外角 第2课时 课件 2023-2024学年初中数学冀教版七年级下册(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 919.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 23:30:13 | ||
图片预览







文档简介
(共21张PPT)
第九章 三角形
9.2 三角形的内角和外角
第2课时
一、学习目标
1.知道三角形外角的概念,会识别三角形的外角;
3.掌握三角形的外角的有关性质,并能运用这些性质解决简单的问题.(重点)
2.知道三角形两种分类方式;
二、新课导入
1.在△ABC中,∠A=80°, ∠B=52°,则∠C= .
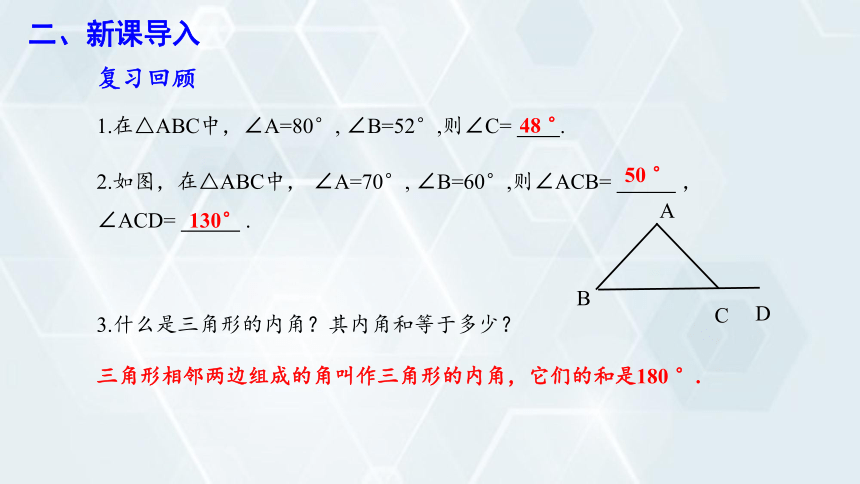
2.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
48 °
50 °
130°
3.什么是三角形的内角?其内角和等于多少?
三角形相邻两边组成的角叫作三角形的内角,它们的和是180 °.
复习回顾
三、自主学习
知识点一:三角形的外角的概念
定义:如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
C
B
A
D
∠ACD是△ABC的一个外角
三、自主学习
问题1: 如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
∠BCE是△ABC的一个外角,
C
B
A
D
E
问题2 : 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
在三角形每个顶点处都有两个外角.
∠DCE不是△ABC的一个外角.
三、自主学习
归纳小结
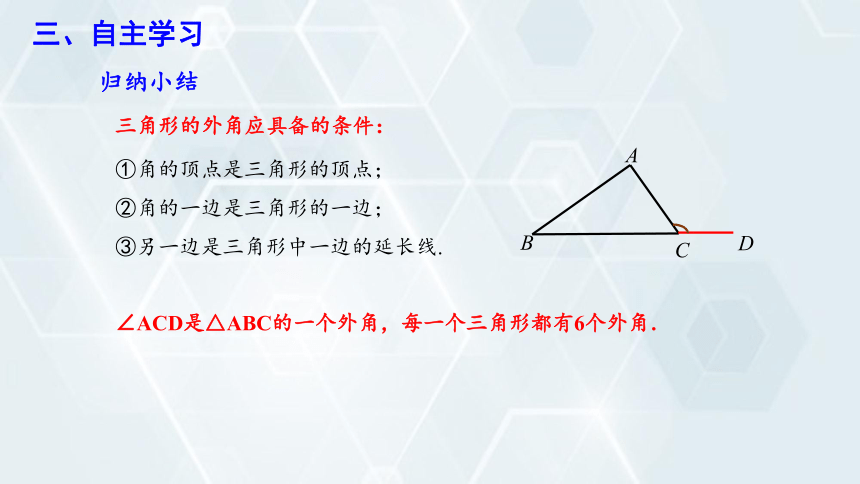
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
C
B
A
D
∠ACD是△ABC的一个外角,每一个三角形都有6个外角.
三、自主学习
知识点二:三角形的外角的性质
三角形外角的性质:如图,∠A+∠B+∠ACB=_____°,∠ACB+∠ACD=_____°,
所以∠A+∠B= .
180
180
∠ACD
即三角形的一个外角等于与它不相邻的两个内角之和.
你能用作平行线的方法说明此结论吗?
三、自主学习
验证结论
已知:如图,△ABC,对∠ACD=∠A+∠B说明理由.
A
B
C
D
1
2
E
解:过C作CE平行于AB,
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
由此也说明:三角形的一个外角_____与它不相邻的任意一个内角.
大于
三、自主学习
三、自主学习
知识点三:三角形的外角和
如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,∠ACD= ∠1+ ∠2.
结论:三角形的外角和等于360°.
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
又知∠1+ ∠2+ ∠3=180 °,
问题:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
三、概念剖析
知识点四:三角形的分类
锐角三角形
直角三角形
钝角三角形
按是否有边相等分
按内角大小分
三角形
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
三、概念剖析
CE平分∠ACD,∠ACE= ______,得出∠ACE的大小.
问题探究:根据三角形外角的性质可知∠ACD=______+______.
四、合作探究
探究一 三角形的外角的性质
问题提出:如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是多少?
∠B
∠ACD
已知∠A和∠B的大小,可求出∠ACD的大小;
∠A
四、合作探究
探究一 三角形的外角的性质
问题提出:如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是多少?
解:∵∠ACD=∠B+∠A,(三角形的一个外角等于与它不相邻的两个内角的和)
而∠A=80°,∠B=40°,
∴∠ACE=60°
∵CE平分∠ACD,
∴∠ACD=80°+40°=120°.
问题解决:
四、合作探究
练一练:
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠ABD=28°, ∠BEC=60°,
∴ ∠BFC=88°.
解:
B
C
A
F
E
D
1.如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
再根据三角形内角和定理得∠BAC+__________=180°,∠BAC=63°,
根据三角形外角的性质可得∠3=∠1+______=∠4=_____,
四、合作探究
探究二 三角形的内外角性质的综合运用
问题提出:如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,
∠BAC=63°,求∠DAC的度数.
问题探究:可设∠1=x,由题干可知∠2=_____,
x
∠2
∠2+∠4
2x
可得方程x+________=180°,
2x+63°
最后通过三角形内角和定理可求出∠DAC的度数.
四、合作探究
解:设∠1=∠2=x,
∴∠DAC=∠BAC-∠1=63°-39°=24°
解得x=39°,即∠1=39°,
∵ ∠BAC=63°,由三角形内角和定理可得:
x+2x+63°=180°
∴∠3=∠4=2x,
∵∠3=∠1+∠2,(三角形的一个外角等于与它不相邻的两个内角之和)
问题提出:如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,
∠BAC=63°,求∠DAC的度数.
问题解决:
2 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:∠B 和∠C的度数.
解:因为∠ADC是△ABD的外角,
四、合作探究
练一练:
∠C=180 -40 -70 =70°.
在△ABC中,∠B+∠BAC+∠C=180°,
所以∠B=80°× =40°,
又因为∠B=∠BAD,
所以∠ADC=∠B+∠BAD=80°,
五、当堂检测
1.将一副三角板如图所示放置,使得两条直角边在一条直线上,则∠1的度数是( )
A.80° B.75°C.60° D.55°
B
五、当堂检测
2.如图,将纸片沿EF折叠,点C落到点C'处,已知∠C'=40°,请求出∠1+∠2的度数.
∵∠AEF=∠C+∠CFE,∠BFE=∠C+∠CEF,
∴∠C=∠C',∠CFE=C'FE,∠CEF=∠C'EF,
∵点C'是点C沿EF折叠所得,
解:∵ ∠C'=40°,
∴∠1+∠2=∠AEF-∠C'EF+∠BFE-∠C'FE=2∠C'=80°.
(三角形的一个外角等于与它不相邻的两个内角之和)
∴∠C'EF+∠C'FE=140°(三角形内角和定理)
五、当堂检测
3.小熊和小猫想把一个三角形纸片折一次后,折痕把原三角形分成两个直角三角形,能做到吗?如果使折痕把原三角形分成两个锐角三角形呢?如果能,说明折的方法,如果不能,说明理由.
锐角三角形的内角均为锐角,一条边上的折痕只能将平角分成两个直角或一个钝角一个锐角,故不能形成两个锐角三角形.
解:把原三角形折成两个直角三角形能做到;
使折痕垂直于三角形的一条边,这样三角形有一个内角是直角,为直角三角形.
折痕不能把原三角形分成两个锐角三角形;
六、课堂总结
三角形的外角和等于360 °
三角形的外角
三角形外角的性质
三角形的分类
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
按边分类
按角分类
等腰三角形
不等边三角形
锐角三角形
直角三角形
钝角三角形
第九章 三角形
9.2 三角形的内角和外角
第2课时
一、学习目标
1.知道三角形外角的概念,会识别三角形的外角;
3.掌握三角形的外角的有关性质,并能运用这些性质解决简单的问题.(重点)
2.知道三角形两种分类方式;
二、新课导入
1.在△ABC中,∠A=80°, ∠B=52°,则∠C= .
2.如图,在△ABC中, ∠A=70°, ∠B=60°,则∠ACB= ,∠ACD= .
A
B
C
D
48 °
50 °
130°
3.什么是三角形的内角?其内角和等于多少?
三角形相邻两边组成的角叫作三角形的内角,它们的和是180 °.
复习回顾
三、自主学习
知识点一:三角形的外角的概念
定义:如图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
C
B
A
D
∠ACD是△ABC的一个外角
三、自主学习
问题1: 如图,延长AC到E,∠BCE是不是△ABC的一个外角?∠DCE是不是△ABC的一个外角?
∠BCE是△ABC的一个外角,
C
B
A
D
E
问题2 : 如图,∠ACD与∠BCE有什么关系?在三角形的每个顶点处有多少个外角?
∠ACD 与∠BCE为对顶角,∠ACD =∠BCE;
在三角形每个顶点处都有两个外角.
∠DCE不是△ABC的一个外角.
三、自主学习
归纳小结
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;
②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
C
B
A
D
∠ACD是△ABC的一个外角,每一个三角形都有6个外角.
三、自主学习
知识点二:三角形的外角的性质
三角形外角的性质:如图,∠A+∠B+∠ACB=_____°,∠ACB+∠ACD=_____°,
所以∠A+∠B= .
180
180
∠ACD
即三角形的一个外角等于与它不相邻的两个内角之和.
你能用作平行线的方法说明此结论吗?
三、自主学习
验证结论
已知:如图,△ABC,对∠ACD=∠A+∠B说明理由.
A
B
C
D
1
2
E
解:过C作CE平行于AB,
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
由此也说明:三角形的一个外角_____与它不相邻的任意一个内角.
大于
三、自主学习
三、自主学习
知识点三:三角形的外角和
如图, ∠BAE, ∠CBF, ∠ACD是△ABC的三个外角,它们的和是多少?
A
B
C
E
F
D
(
(
(
(
(
(
2
1
3
解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE= ∠2+ ∠3,
∠CBF= ∠1+ ∠3,∠ACD= ∠1+ ∠2.
结论:三角形的外角和等于360°.
所以∠BAE+ ∠CBF+ ∠ACD
=2(∠1+ ∠2+ ∠3)=360 °.
又知∠1+ ∠2+ ∠3=180 °,
问题:按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形
直角三角形
钝角三角形
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
三、概念剖析
知识点四:三角形的分类
锐角三角形
直角三角形
钝角三角形
按是否有边相等分
按内角大小分
三角形
三角形
不等边三角形
等腰
三角形
底和腰不相等的等腰三角形
等边三角形
三、概念剖析
CE平分∠ACD,∠ACE= ______,得出∠ACE的大小.
问题探究:根据三角形外角的性质可知∠ACD=______+______.
四、合作探究
探究一 三角形的外角的性质
问题提出:如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是多少?
∠B
∠ACD
已知∠A和∠B的大小,可求出∠ACD的大小;
∠A
四、合作探究
探究一 三角形的外角的性质
问题提出:如图,点D在△ABC边BC的延长线上,CE平分∠ACD,∠A=80°,∠B=40°,则∠ACE的大小是多少?
解:∵∠ACD=∠B+∠A,(三角形的一个外角等于与它不相邻的两个内角的和)
而∠A=80°,∠B=40°,
∴∠ACE=60°
∵CE平分∠ACD,
∴∠ACD=80°+40°=120°.
问题解决:
四、合作探究
练一练:
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,(三角形的一个外角等于与它不相邻的两个内角的和)
∵ ∠ABD=28°, ∠BEC=60°,
∴ ∠BFC=88°.
解:
B
C
A
F
E
D
1.如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
再根据三角形内角和定理得∠BAC+__________=180°,∠BAC=63°,
根据三角形外角的性质可得∠3=∠1+______=∠4=_____,
四、合作探究
探究二 三角形的内外角性质的综合运用
问题提出:如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,
∠BAC=63°,求∠DAC的度数.
问题探究:可设∠1=x,由题干可知∠2=_____,
x
∠2
∠2+∠4
2x
可得方程x+________=180°,
2x+63°
最后通过三角形内角和定理可求出∠DAC的度数.
四、合作探究
解:设∠1=∠2=x,
∴∠DAC=∠BAC-∠1=63°-39°=24°
解得x=39°,即∠1=39°,
∵ ∠BAC=63°,由三角形内角和定理可得:
x+2x+63°=180°
∴∠3=∠4=2x,
∵∠3=∠1+∠2,(三角形的一个外角等于与它不相邻的两个内角之和)
问题提出:如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,
∠BAC=63°,求∠DAC的度数.
问题解决:
2 .如图,D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:∠B 和∠C的度数.
解:因为∠ADC是△ABD的外角,
四、合作探究
练一练:
∠C=180 -40 -70 =70°.
在△ABC中,∠B+∠BAC+∠C=180°,
所以∠B=80°× =40°,
又因为∠B=∠BAD,
所以∠ADC=∠B+∠BAD=80°,
五、当堂检测
1.将一副三角板如图所示放置,使得两条直角边在一条直线上,则∠1的度数是( )
A.80° B.75°C.60° D.55°
B
五、当堂检测
2.如图,将纸片沿EF折叠,点C落到点C'处,已知∠C'=40°,请求出∠1+∠2的度数.
∵∠AEF=∠C+∠CFE,∠BFE=∠C+∠CEF,
∴∠C=∠C',∠CFE=C'FE,∠CEF=∠C'EF,
∵点C'是点C沿EF折叠所得,
解:∵ ∠C'=40°,
∴∠1+∠2=∠AEF-∠C'EF+∠BFE-∠C'FE=2∠C'=80°.
(三角形的一个外角等于与它不相邻的两个内角之和)
∴∠C'EF+∠C'FE=140°(三角形内角和定理)
五、当堂检测
3.小熊和小猫想把一个三角形纸片折一次后,折痕把原三角形分成两个直角三角形,能做到吗?如果使折痕把原三角形分成两个锐角三角形呢?如果能,说明折的方法,如果不能,说明理由.
锐角三角形的内角均为锐角,一条边上的折痕只能将平角分成两个直角或一个钝角一个锐角,故不能形成两个锐角三角形.
解:把原三角形折成两个直角三角形能做到;
使折痕垂直于三角形的一条边,这样三角形有一个内角是直角,为直角三角形.
折痕不能把原三角形分成两个锐角三角形;
六、课堂总结
三角形的外角和等于360 °
三角形的外角
三角形外角的性质
三角形的分类
三角形的一个外角等于与它不相邻的两个内角的和.
三角形的一个外角大于与它不相邻的任意一个内角.
按边分类
按角分类
等腰三角形
不等边三角形
锐角三角形
直角三角形
钝角三角形
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
