8.4 整式的乘法 第1课时 课件(共15张PPT) 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 8.4 整式的乘法 第1课时 课件(共15张PPT) 2023-2024学年初中数学冀教版七年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 984.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 08:19:19 | ||
图片预览






文档简介
(共15张PPT)
第八章 整式的乘法
8.4 整式的乘法
第1课时
一、学习目标
1.掌握单项式与单项式相乘的运算法则;
2.能够灵活地进行单项式与单项式相乘的运算.(重点)
二、新课导入
复习引入
幂的运算性质有哪几条?
同底数幂的乘法法则:am·an=am+n ( m、n都是正整数).
幂的乘方法则:(am)n=amn ( m、n都是正整数).
积的乘方法则:(ab)n=anbn( m、n都是正整数).
三、合作探究
探究一 单项式与单项式乘法法则
问题提出:
光的速度约为3×105km/s,太阳光照射到地球上需要的时间
大约是5×102s,你知道地球与太阳的距离约是多少千米吗
(3×105)×(5×102)km
地球与太阳的距离约是
三、合作探究
想一想: (1)怎样计算(3 ×105)×(5 ×102)?计算过程中
用到了哪些运算律及运算性质?
利用乘法交换律和结合律有
(3×105)×(5×102)=(_____)×(105×102)=15×107.
3×5
三、合作探究
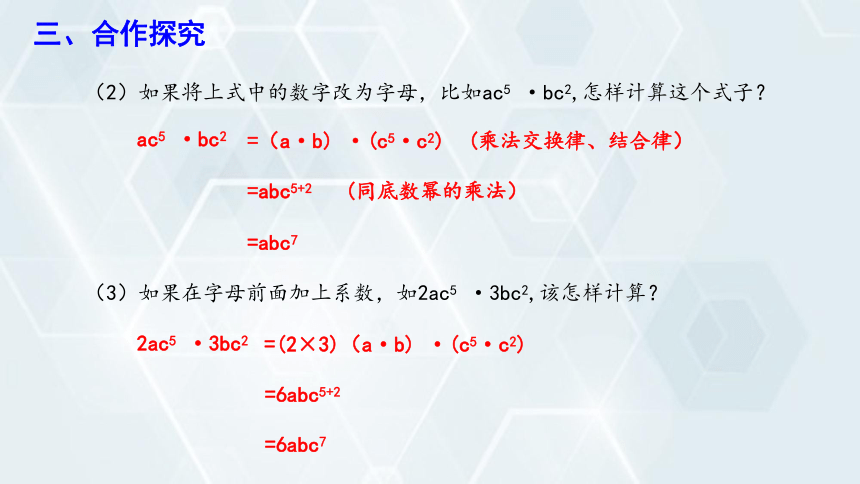
(2)如果将上式中的数字改为字母,比如ac5 ·bc2,怎样计算这个式子?
ac5 ·bc2
(3)如果在字母前面加上系数,如2ac5 ·3bc2,该怎样计算?
2ac5 ·3bc2
=(a·b) ·(c5·c2) (乘法交换律、结合律)
=abc5+2 (同底数幂的乘法)
=abc7
=(2×3)(a·b) ·(c5·c2)
=6abc5+2
=6abc7
三、合作探究
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它们的指数作为积的一个因式.
注意:
要点归纳
单项式的乘法法则
(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
三、合作探究
练一练
1.计算:(1) (5x3)(2x2y); (2)(-5a2b3)(-4b2c)
解:
小结:单项式与单项式相乘本质就是通过乘法的交换律和结合律,
转化为有理数的乘法与同底数幂的乘法.
原式
=(5×2)(x3·x2)y
=10x5y
解:
原式
=(-5)×(-4) a2(b3 b2) c
= 20a2b5c
三、合作探究
探究二 单项式乘单项式的计算
问题提出:如何计算(3a)2·(-2ab)3.
问题探究:运算顺序应为先 ,再乘除.
乘方
(3a)2= ,(-2ab)3= .
9a2
-8a3b3
因此原式=9a2·(-8a3b3).
再利用单项式的乘法法则:
9a2·(-8a3b3)=[9×( )]·( )= .
-8
a5b3
-72a5b3
问题解决:
(3a)2·(-2ab)3
=9a2·(-8a3b3)
=[9×(-8)]·a5b3
=-72a5b3.
三、合作探究
练一练
2.计算:(1) (2x)3(-5xy3); (2) 5a3b (-a)4 (-b2)2
解:
小结:有乘方运算,先算乘方,再算单项式相乘.
原式
=8x3(-5xy3)
=[8×(-5)](x3 x)y3
=-40x4y3.
解:
原式
= 5a3b a4 b4
= 5(a3 a4)(b b4)
= 5a7b5
四、当堂检测
1.计算:
解: 原式=(2×3)(x2·x3)
原式=-2.5x2·16x2
=6x5;
=-(2.5×16)(x2·x2)
=-40x4;
(3)(-2.5x2) ·(-4x)2 (4)(-4x2y)(-xy)2(- y3)
(1) 2x2 ·3x3 (2) a2b3· abc
原式=( × )·a3b4c
= a3b4c;
原式=(-4x2y)·(x2y2)·( y3)
=[-4×( )]·x4y6
=2x4y6.
四、当堂检测
2.计算:
(1)(4×105)×(5×106)×(3×104);
(2)2a2·(-2a)2+2a3·5a.
解:
(1)原式=(4×5×3)×(105×106×104)
=60×1015
=6×1016;
(2)原式=2a2·4a2+10a4
=8a4+10a4
=18a4.
四、当堂检测
(3)(2x2)3 x2-x10÷x2
解:
(3)原式=8x6·x2-x8
=8x8-x8
=7x8
四、当堂检测
3.光在真空中的速度约是3×108m/s,光在真空中穿行1年的距离称为1光年.
请你算算:1年以3×107s计算,1光年约是多少千米?
解:1光年=(3×108)×(3×107)
=(3×3)×(108×107)=9×1015m =9×1012km.
答:1光年约是9×1012km.
五、课堂总结
单项式乘
单项式
实质上是转化为有理数的乘法与
同底数幂的乘法
系数相乘
相同字母的幂相乘
其余字母连同它的指数不变,作为积的因式
第八章 整式的乘法
8.4 整式的乘法
第1课时
一、学习目标
1.掌握单项式与单项式相乘的运算法则;
2.能够灵活地进行单项式与单项式相乘的运算.(重点)
二、新课导入
复习引入
幂的运算性质有哪几条?
同底数幂的乘法法则:am·an=am+n ( m、n都是正整数).
幂的乘方法则:(am)n=amn ( m、n都是正整数).
积的乘方法则:(ab)n=anbn( m、n都是正整数).
三、合作探究
探究一 单项式与单项式乘法法则
问题提出:
光的速度约为3×105km/s,太阳光照射到地球上需要的时间
大约是5×102s,你知道地球与太阳的距离约是多少千米吗
(3×105)×(5×102)km
地球与太阳的距离约是
三、合作探究
想一想: (1)怎样计算(3 ×105)×(5 ×102)?计算过程中
用到了哪些运算律及运算性质?
利用乘法交换律和结合律有
(3×105)×(5×102)=(_____)×(105×102)=15×107.
3×5
三、合作探究
(2)如果将上式中的数字改为字母,比如ac5 ·bc2,怎样计算这个式子?
ac5 ·bc2
(3)如果在字母前面加上系数,如2ac5 ·3bc2,该怎样计算?
2ac5 ·3bc2
=(a·b) ·(c5·c2) (乘法交换律、结合律)
=abc5+2 (同底数幂的乘法)
=abc7
=(2×3)(a·b) ·(c5·c2)
=6abc5+2
=6abc7
三、合作探究
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它们的指数作为积的一个因式.
注意:
要点归纳
单项式的乘法法则
(1)系数相乘;
(2)相同字母的幂相乘;
(3)其余字母连同它的指数不变,作为积的因式.
三、合作探究
练一练
1.计算:(1) (5x3)(2x2y); (2)(-5a2b3)(-4b2c)
解:
小结:单项式与单项式相乘本质就是通过乘法的交换律和结合律,
转化为有理数的乘法与同底数幂的乘法.
原式
=(5×2)(x3·x2)y
=10x5y
解:
原式
=(-5)×(-4) a2(b3 b2) c
= 20a2b5c
三、合作探究
探究二 单项式乘单项式的计算
问题提出:如何计算(3a)2·(-2ab)3.
问题探究:运算顺序应为先 ,再乘除.
乘方
(3a)2= ,(-2ab)3= .
9a2
-8a3b3
因此原式=9a2·(-8a3b3).
再利用单项式的乘法法则:
9a2·(-8a3b3)=[9×( )]·( )= .
-8
a5b3
-72a5b3
问题解决:
(3a)2·(-2ab)3
=9a2·(-8a3b3)
=[9×(-8)]·a5b3
=-72a5b3.
三、合作探究
练一练
2.计算:(1) (2x)3(-5xy3); (2) 5a3b (-a)4 (-b2)2
解:
小结:有乘方运算,先算乘方,再算单项式相乘.
原式
=8x3(-5xy3)
=[8×(-5)](x3 x)y3
=-40x4y3.
解:
原式
= 5a3b a4 b4
= 5(a3 a4)(b b4)
= 5a7b5
四、当堂检测
1.计算:
解: 原式=(2×3)(x2·x3)
原式=-2.5x2·16x2
=6x5;
=-(2.5×16)(x2·x2)
=-40x4;
(3)(-2.5x2) ·(-4x)2 (4)(-4x2y)(-xy)2(- y3)
(1) 2x2 ·3x3 (2) a2b3· abc
原式=( × )·a3b4c
= a3b4c;
原式=(-4x2y)·(x2y2)·( y3)
=[-4×( )]·x4y6
=2x4y6.
四、当堂检测
2.计算:
(1)(4×105)×(5×106)×(3×104);
(2)2a2·(-2a)2+2a3·5a.
解:
(1)原式=(4×5×3)×(105×106×104)
=60×1015
=6×1016;
(2)原式=2a2·4a2+10a4
=8a4+10a4
=18a4.
四、当堂检测
(3)(2x2)3 x2-x10÷x2
解:
(3)原式=8x6·x2-x8
=8x8-x8
=7x8
四、当堂检测
3.光在真空中的速度约是3×108m/s,光在真空中穿行1年的距离称为1光年.
请你算算:1年以3×107s计算,1光年约是多少千米?
解:1光年=(3×108)×(3×107)
=(3×3)×(108×107)=9×1015m =9×1012km.
答:1光年约是9×1012km.
五、课堂总结
单项式乘
单项式
实质上是转化为有理数的乘法与
同底数幂的乘法
系数相乘
相同字母的幂相乘
其余字母连同它的指数不变,作为积的因式
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
