8.4 整式的乘法( 第3课时) 课件 16张PPT 2023-2024学年初中数学冀教版七年级下册
文档属性
| 名称 | 8.4 整式的乘法( 第3课时) 课件 16张PPT 2023-2024学年初中数学冀教版七年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 878.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第八章 整式的乘法
8.4 整式的乘法
第3课时
一、学习目标
1.掌握多项式与多项式的乘法运算法则.
2.能熟练地进行多项式与多项式的乘法运算.(重点)
二、新课导入
复习引入
1.如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项,
2.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘;
② 去括号时注意符号的确定.
探究一 多项式与多项式乘法法则
自主探究
问题1: (a+b)X= .
那当X=(m+n),(a+b)X=(a+b)× = a× +b× .
(m+n)
(m+n)
(m+n)
aX+bX
计算过程中你运用了 与 的乘法法则.
单项式
多项式
想一想: 通过上面的解答过程,你是否已经对多项式乘多项式的运算
有了初步的思路了呢?
三、合作探究
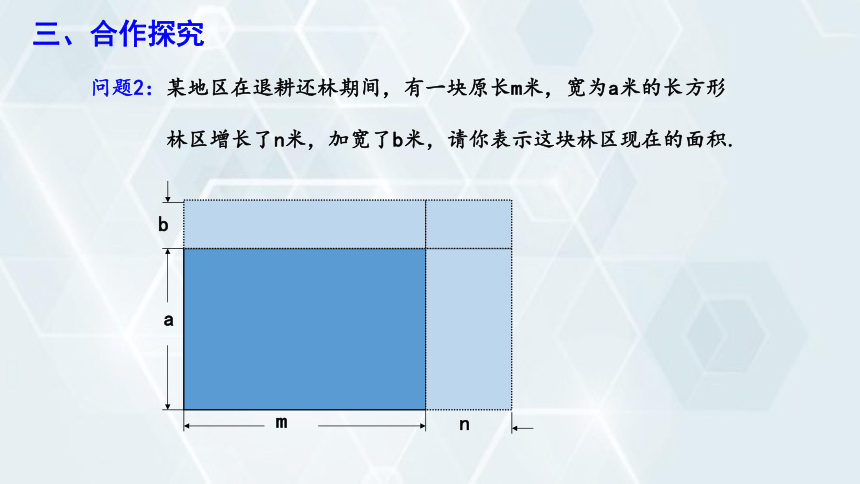
问题2:某地区在退耕还林期间,有一块原长m米,宽为a米的长方形
林区增长了n米,加宽了b米,请你表示这块林区现在的面积.
a
m
b
n
三、合作探究
a
m
b
n
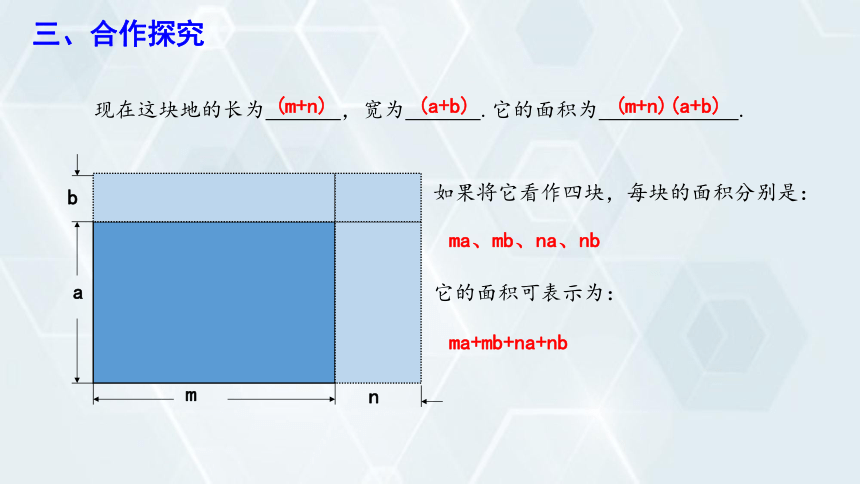
现在这块地的长为 ,宽为 .它的面积为 .
如果将它看作四块,每块的面积分别是:
它的面积可表示为:
(a+b)
(m+n)
(m+n)(a+b)
ma、mb、na、nb
ma+mb+na+nb
三、合作探究
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb
实际上,把(m+n)看成一个整体,有:
ma+mb+na+nb
(m+n)(a+b)=
(m+n)a+(m+n)b
这是单项式乘多项式的形式,我们可以运用其法则进行计算.
=
三、合作探究
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式
的每一项相乘,再把所得的积相加.
注意:
要点归纳
多项式乘多项式的法则
(1)多项式的各项之间都要进行一次相乘;(同一多项式的各项之间不能相乘)
(2)各项相乘后结果要相加.
(m+n)(a+b)=
ma
mb
na
nb
+
+
+
三、合作探究
练一练
计算:(1)(3x+1)(x+2); (2)(x-8)(x-y);
=x2-xy-8x+8y;
解:
三、合作探究
(1)原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(3) (x+y)(x2-xy+y2).
(2) 原式=x·x-xy-8x+8y
(3)原式 =x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
探究二 多项式乘多项式的应用
活动:如图,在某住房小区的建设中,为了提高业主的居住环境,小区准
备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽
为b米的通道.
(1)用字母a和b表示剩余草坪的面积
4a+3b
2a+3b
b
b
+b2
(4a+3b)(2a+3b)-b(2a+3b)-b(4a+3b)
=8a2+6ab+12ab+9b2-6ab-5b2
=8a2+12ab+4b2(平方米),
三、合作探究
4a+3b
2a+3b
b
b
想一想:有没有别方法计算更简单呢?
4a+3b
2a+3b
b
b
(4a+3b-b)(2a+3b-b)
(2)当a=2,b=1时,剩余草坪的面积是多少?
当a=2,b=1;8a2+12ab+4b2=
=(4a+2b)(2a+2b)
=8a2+12ab+4b2(平方米)
8×4+12×2×1+4×1
=60(平方米)
三、合作探究
练一练
2.我们用的书除了中间的文字区域外,通常在它的左右两边都留有宽为a的空白,顶部和底部都留有宽为b的空白,如图.若纸的长和宽分别为x,y,求中间文字区域的面积.
分析:纸的面积减去空白的面积即为文字区域面积,
可以看作上方有2b的空白区域,左边有2a的空白区域,其余都为文字区域.
解:(x-2b)(y-2a)
答:中间文字区域的面积为xy-2ax-2by+4ab.
三、合作探究
a
a
b
b
=xy-2ax-2by+4ab
四、当堂检测
1.判断下面计算过程是否正确.如果错误,请给出正确答案.
(1)(x-1)2=x2-12=x2-1 ( )
×
(2)(2x-3)(x-2)=2x2-4x+6 ( )
×
(1)(x-1)2=(x-1)(x-1)=x2-x-x+1=x2-2x+1.
(2)(2x-3)(x-2)=2x2-4x-3x+6=2x2-7x+6
注意:1.(a-b)2也是多项式的相乘,不能用幂的乘方法则去进行运算.
2.进行多项式与多项式相乘运算时不要漏乘.
四、当堂检测
2.(1)计算:3x(x+2)-(x+1)(3x-4)
解: (x-2)(2x-5)-2(x-1)(x+1)=3
2x2-9x+10-2x2+2=3
x=1
9x=9
解:原式=3x2+6x-(3x2-4x+3x-4)
=3x2+6x-3x2+4x-3x+4
=7x+4
(2)解方程:(x-2)(2x-5)-2(x-1)(x+1)=3
四、当堂检测
3.先化简,再求值:
5x(2x+1)-(2x+3)(5x-1) 其中,x=13.
解:原式=10x2+5x-(10x2-2x+15x-3)
=10x2+5x-10x2+2x-15x+3
=-8x+3
当x=13时,
原式=-8×13+3=-101
五、课堂总结
多项式乘多项式
运算法则
注意事项
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(1)不要漏乘;
(2)正确确认各部分的符号; (3)结果需要化为最简形式.
实质上是转化为单项式乘单项式
第八章 整式的乘法
8.4 整式的乘法
第3课时
一、学习目标
1.掌握多项式与多项式的乘法运算法则.
2.能熟练地进行多项式与多项式的乘法运算.(重点)
二、新课导入
复习引入
1.如何进行单项式与多项式乘法的运算?
② 再把所得的积相加.
① 将单项式分别乘以多项式的各项,
2.进行单项式与多项式乘法运算时,要注意什么
① 不能漏乘;
② 去括号时注意符号的确定.
探究一 多项式与多项式乘法法则
自主探究
问题1: (a+b)X= .
那当X=(m+n),(a+b)X=(a+b)× = a× +b× .
(m+n)
(m+n)
(m+n)
aX+bX
计算过程中你运用了 与 的乘法法则.
单项式
多项式
想一想: 通过上面的解答过程,你是否已经对多项式乘多项式的运算
有了初步的思路了呢?
三、合作探究
问题2:某地区在退耕还林期间,有一块原长m米,宽为a米的长方形
林区增长了n米,加宽了b米,请你表示这块林区现在的面积.
a
m
b
n
三、合作探究
a
m
b
n
现在这块地的长为 ,宽为 .它的面积为 .
如果将它看作四块,每块的面积分别是:
它的面积可表示为:
(a+b)
(m+n)
(m+n)(a+b)
ma、mb、na、nb
ma+mb+na+nb
三、合作探究
由于(m+n)(a+b)和(ma+mb+na+nb)表示同一块地的面积,故有:
(m+n)(a+b)=
ma
+ mb
+ na
+ nb
实际上,把(m+n)看成一个整体,有:
ma+mb+na+nb
(m+n)(a+b)=
(m+n)a+(m+n)b
这是单项式乘多项式的形式,我们可以运用其法则进行计算.
=
三、合作探究
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式
的每一项相乘,再把所得的积相加.
注意:
要点归纳
多项式乘多项式的法则
(1)多项式的各项之间都要进行一次相乘;(同一多项式的各项之间不能相乘)
(2)各项相乘后结果要相加.
(m+n)(a+b)=
ma
mb
na
nb
+
+
+
三、合作探究
练一练
计算:(1)(3x+1)(x+2); (2)(x-8)(x-y);
=x2-xy-8x+8y;
解:
三、合作探究
(1)原式=3x·x+2×3x+1·x+1×2
=3x2+6x+x+2
=3x2+7x+2;
(3) (x+y)(x2-xy+y2).
(2) 原式=x·x-xy-8x+8y
(3)原式 =x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
探究二 多项式乘多项式的应用
活动:如图,在某住房小区的建设中,为了提高业主的居住环境,小区准
备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽
为b米的通道.
(1)用字母a和b表示剩余草坪的面积
4a+3b
2a+3b
b
b
+b2
(4a+3b)(2a+3b)-b(2a+3b)-b(4a+3b)
=8a2+6ab+12ab+9b2-6ab-5b2
=8a2+12ab+4b2(平方米),
三、合作探究
4a+3b
2a+3b
b
b
想一想:有没有别方法计算更简单呢?
4a+3b
2a+3b
b
b
(4a+3b-b)(2a+3b-b)
(2)当a=2,b=1时,剩余草坪的面积是多少?
当a=2,b=1;8a2+12ab+4b2=
=(4a+2b)(2a+2b)
=8a2+12ab+4b2(平方米)
8×4+12×2×1+4×1
=60(平方米)
三、合作探究
练一练
2.我们用的书除了中间的文字区域外,通常在它的左右两边都留有宽为a的空白,顶部和底部都留有宽为b的空白,如图.若纸的长和宽分别为x,y,求中间文字区域的面积.
分析:纸的面积减去空白的面积即为文字区域面积,
可以看作上方有2b的空白区域,左边有2a的空白区域,其余都为文字区域.
解:(x-2b)(y-2a)
答:中间文字区域的面积为xy-2ax-2by+4ab.
三、合作探究
a
a
b
b
=xy-2ax-2by+4ab
四、当堂检测
1.判断下面计算过程是否正确.如果错误,请给出正确答案.
(1)(x-1)2=x2-12=x2-1 ( )
×
(2)(2x-3)(x-2)=2x2-4x+6 ( )
×
(1)(x-1)2=(x-1)(x-1)=x2-x-x+1=x2-2x+1.
(2)(2x-3)(x-2)=2x2-4x-3x+6=2x2-7x+6
注意:1.(a-b)2也是多项式的相乘,不能用幂的乘方法则去进行运算.
2.进行多项式与多项式相乘运算时不要漏乘.
四、当堂检测
2.(1)计算:3x(x+2)-(x+1)(3x-4)
解: (x-2)(2x-5)-2(x-1)(x+1)=3
2x2-9x+10-2x2+2=3
x=1
9x=9
解:原式=3x2+6x-(3x2-4x+3x-4)
=3x2+6x-3x2+4x-3x+4
=7x+4
(2)解方程:(x-2)(2x-5)-2(x-1)(x+1)=3
四、当堂检测
3.先化简,再求值:
5x(2x+1)-(2x+3)(5x-1) 其中,x=13.
解:原式=10x2+5x-(10x2-2x+15x-3)
=10x2+5x-10x2+2x-15x+3
=-8x+3
当x=13时,
原式=-8×13+3=-101
五、课堂总结
多项式乘多项式
运算法则
注意事项
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(1)不要漏乘;
(2)正确确认各部分的符号; (3)结果需要化为最简形式.
实质上是转化为单项式乘单项式
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
