北京市第一五六中学2023~2024学年下学期八年级开学考数学试卷(pdf版 无答案)
文档属性
| 名称 | 北京市第一五六中学2023~2024学年下学期八年级开学考数学试卷(pdf版 无答案) |  | |
| 格式 | |||
| 文件大小 | 658.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 10:36:47 | ||
图片预览

文档简介
八年级数学摸底考试
一、选择题
1.若正比例函数 y kx的图像经过点(1,2),则 k 的值为( )
1 1
A. B.-2 C. D.2
2 2
2.下列各曲线中不能表示 y 是 x 的函数的是( )
v
0 x
A B C D
3. 将正比例函数 y=3x 的图象向下平移 4 个单位长度后,所得函数图象的解析式为
( ).
A. y 3x 4 B. y 3x 4
C. y 3(x 4) D. y 3(x 4)
4.如图,三条公路把 A、B、C 三个村庄连成一个三角形区域,某地区决定在这个
三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个
集贸市场应建在( ).
B
A.在 AC、BC 两边高线的交点处
B.在 AC、BC 两边中线的交点处
C.在∠A、∠B 两内角平分线的交点处
D.在 AC、BC 两边垂直平分线的交点处 A C
5.如图,△ACB≌△A C B , BCB =30°,则 ACA A A
的度数为( ).
B
A.20° B.30°
C.35° D.40°
B
C
6.一次函数 y mx m(m 为常数且 m≠0),若 y 随 x 增大而增大,则它的图象经
( ).
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
1
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
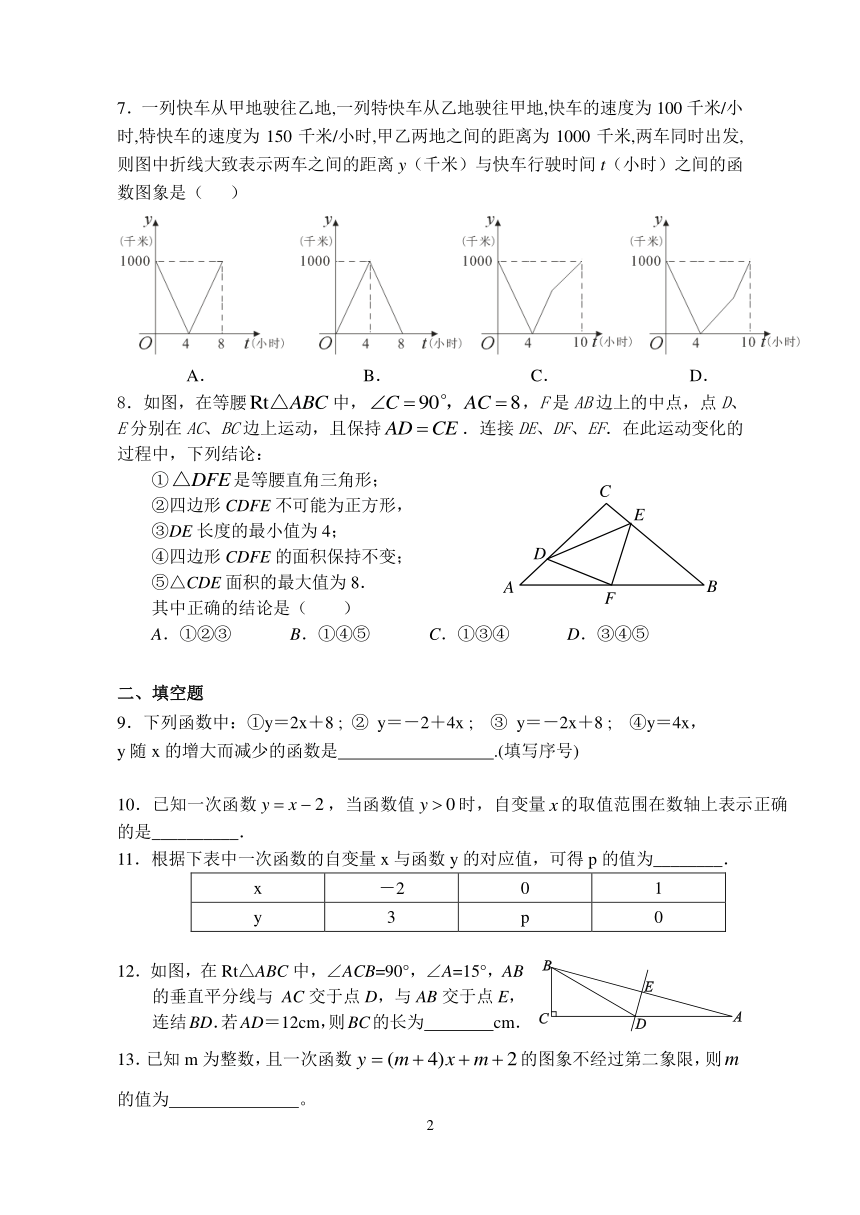
7.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为 100 千米/小
时,特快车的速度为 150 千米/小时,甲乙两地之间的距离为 1000 千米,两车同时出发,
则图中折线大致表示两车之间的距离 y(千米)与快车行驶时间 t(小时)之间的函
数图象是( )
A. B. C. D.
8.如图,在等腰Rt△ABC 中, C 90°,AC 8,F是 AB边上的中点,点 D、
E分别在 AC、BC边上运动,且保持 AD CE .连接 DE、DF、EF.在此运动变化的
过程中,下列结论:
①△DFE是等腰直角三角形;
C
②四边形 CDFE 不可能为正方形,
E
③DE 长度的最小值为 4;
④四边形 CDFE 的面积保持不变; D
⑤△CDE 面积的最大值为 8. A B
F
其中正确的结论是( )
A.①②③ B.①④⑤ C.①③④ D.③④⑤
二、填空题
9.下列函数中:①y=2x+8 ; ② y=-2+4x ; ③ y=-2x+8 ; ④y=4x,
y 随 x 的增大而减少的函数是 .(填写序号)
10.已知一次函数 y x 2 ,当函数值 y 0 时,自变量 x的取值范围在数轴上表示正确
的是__________.
11.根据下表中一次函数的自变量 x 与函数 y 的对应值,可得 p 的值为________.
x -2 0 1
y 3 p 0
12.如图,在 Rt△ABC 中,∠ACB=90°,∠A=15°,AB
的垂直平分线与 AC 交于点 D,与 AB 交于点 E,
连结BD.若AD=12cm,则BC的长为 cm.
13.已知 m 为整数,且一次函数 y (m 4)x m 2的图象不经过第二象限,则m
的值为 。
2
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
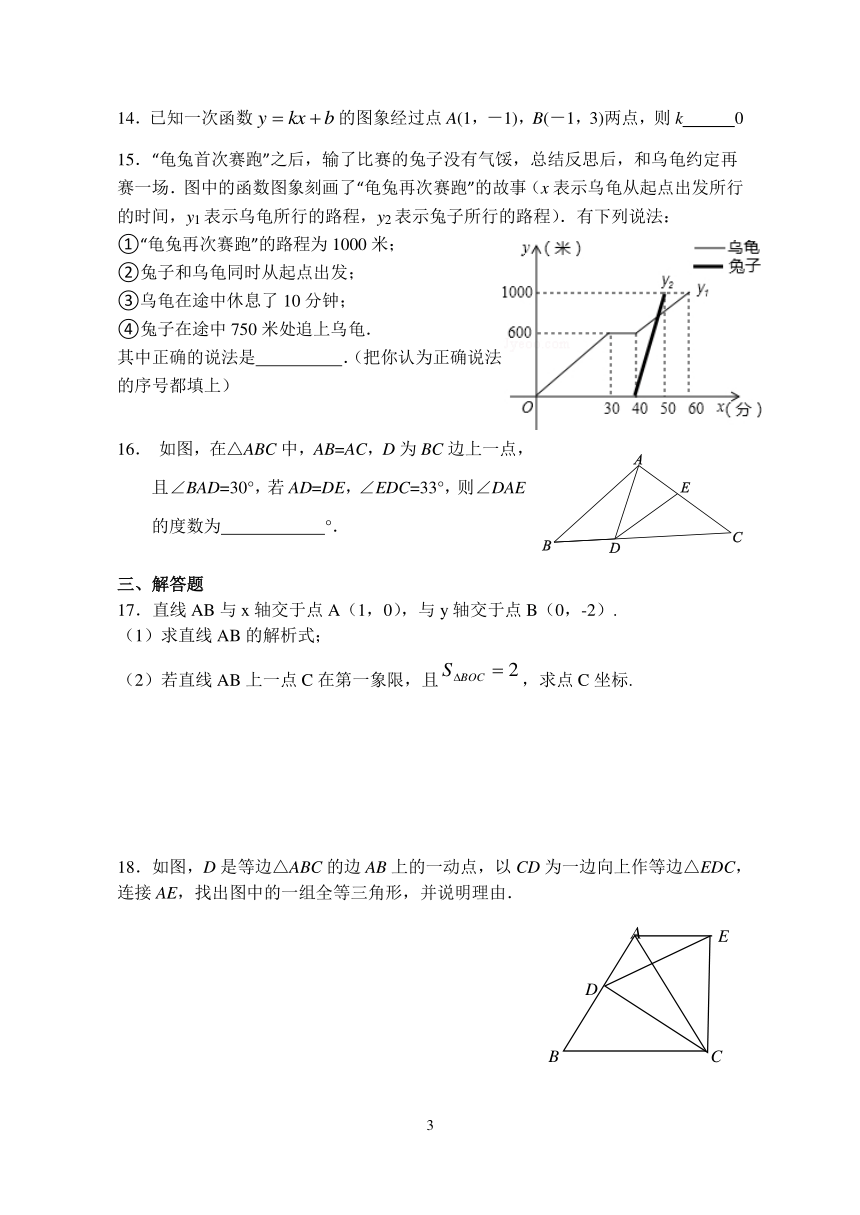
14.已知一次函数 y kx b 的图象经过点 A(1,-1),B(-1,3)两点,则 k 0
15.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再
赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x 表示乌龟从起点出发所行
的时间,y1 表示乌龟所行的路程,y2 表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为 1000 米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了 10 分钟;
④兔子在途中 750 米处追上乌龟.
其中正确的说法是 .(把你认为正确说法
的序号都填上)
16. 如图,在△ABC 中,AB=AC,D 为 BC 边上一点,
且∠BAD=30°,若 AD=DE,∠EDC=33°,则∠DAE
的度数为 °.
三、解答题
17.直线 AB 与 x 轴交于点 A(1,0),与 y 轴交于点 B(0,-2).
(1)求直线 AB 的解析式;
S 2
(2)若直线 AB 上一点 C 在第一象限,且 BOC ,求点 C 坐标.
18.如图,D 是等边△ABC 的边 AB 上的一动点,以 CD 为一边向上作等边△EDC,
连接 AE,找出图中的一组全等三角形,并说明理由.
A E
D
B C
3
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
19.如图,把矩形纸片 ABCD 沿 EF 折叠,使点 B 落在边 AD 上的点 B′处,点 A 落
在点 A′处,求证:B′ E=BF。
20.如图,在△ABC中,∠CAB的平分线 AD 与 BC的垂直平分线 DE交于点 D,DM⊥AB
于 M,DN⊥AC交 AC的延长线于 N. 求证:BM=CN .
证明:
A
M
E
B C
N
D
21.(1)如图 1,A、B是直线 l 同旁的两个定点.请你在直线 l 上确定一点 P,使 PA+PB
的值最小.
B
B
A P
l
O A
图1 图2
(2)如图 2,∠AOB=30°,P 是∠AOB 内一点,PO=10.请你在 OA 上找一点 Q,在
OB 上找一点 R,使得△PQR 的周长最小.要求:画出图形,并计算这个最小值
是 。 .
4
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
4
22.如图,直线 4 4y x 4与y轴交于点 A,与直线 y x 交于点 B,且直线
3 5 5
4 4
y x 与 x 轴交于点 C,求 ABC 的面积.
5 5
23.甲乙两人同时登西山,甲、乙两人距地面的高度 y (米)与登山时间 x (分)
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在 A 地提速时距地面的高度b 为 米.
(2)若乙提速后,乙的速度是甲登山速度的 3倍,请分别求出甲、乙二人登山全过
程中,登山时距地面的高度 y (米)与登山时间 x (分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲?此时乙距 A 地的高度为多少米?
5
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
1
24. 在直角坐标系中,点 A(4,0),点 P(x,y)是直线 y x 3在第一象限
2
的一点.(1)设△OAP 的面积为 S,用含 x的解析式表示 S,写出自变量取值范围.
1
(2)在直线 y x 3求一点 Q,使△OAQ 是以 OA为底的等腰三角形.
2
(3)若第(2)问变为使△OAQ 是等腰三角形,这样的点有几个?
25.将二个全等的 Rt△ABC与 Rt△DBE按图①的方式摆放。其中∠DEB=∠ACB=90°,
∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F。(1)求证:AF+EF=DE;
(2)若将图①中的△DBE 绕 B点按顺时针方向旋转角α,且 0°≤α≤60°,其他了
条件不变,请在图②中画出变换后的图形,并直接写出(1)中的结论是否成立;
(3) 若将图①中的△DBE 绕 B 点按顺时针方向旋转角 β,且 60°≤β≤180°,其
他了条件不变,如图③。你认为(1)中的结论是否成立吗?若成立,写出证明过程,
若不成立,请写出这时 AF、EF和 DE之间的关系,并说明理由。
D
B
E
B B
E
F AC
C A
F C A D
图① 图② 图③
6
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
一、选择题
1.若正比例函数 y kx的图像经过点(1,2),则 k 的值为( )
1 1
A. B.-2 C. D.2
2 2
2.下列各曲线中不能表示 y 是 x 的函数的是( )
v
0 x
A B C D
3. 将正比例函数 y=3x 的图象向下平移 4 个单位长度后,所得函数图象的解析式为
( ).
A. y 3x 4 B. y 3x 4
C. y 3(x 4) D. y 3(x 4)
4.如图,三条公路把 A、B、C 三个村庄连成一个三角形区域,某地区决定在这个
三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个
集贸市场应建在( ).
B
A.在 AC、BC 两边高线的交点处
B.在 AC、BC 两边中线的交点处
C.在∠A、∠B 两内角平分线的交点处
D.在 AC、BC 两边垂直平分线的交点处 A C
5.如图,△ACB≌△A C B , BCB =30°,则 ACA A A
的度数为( ).
B
A.20° B.30°
C.35° D.40°
B
C
6.一次函数 y mx m(m 为常数且 m≠0),若 y 随 x 增大而增大,则它的图象经
( ).
A.第一、二、三象限 B.第一、二、四象限
C.第一、三、四象限 D.第二、三、四象限
1
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
7.一列快车从甲地驶往乙地,一列特快车从乙地驶往甲地,快车的速度为 100 千米/小
时,特快车的速度为 150 千米/小时,甲乙两地之间的距离为 1000 千米,两车同时出发,
则图中折线大致表示两车之间的距离 y(千米)与快车行驶时间 t(小时)之间的函
数图象是( )
A. B. C. D.
8.如图,在等腰Rt△ABC 中, C 90°,AC 8,F是 AB边上的中点,点 D、
E分别在 AC、BC边上运动,且保持 AD CE .连接 DE、DF、EF.在此运动变化的
过程中,下列结论:
①△DFE是等腰直角三角形;
C
②四边形 CDFE 不可能为正方形,
E
③DE 长度的最小值为 4;
④四边形 CDFE 的面积保持不变; D
⑤△CDE 面积的最大值为 8. A B
F
其中正确的结论是( )
A.①②③ B.①④⑤ C.①③④ D.③④⑤
二、填空题
9.下列函数中:①y=2x+8 ; ② y=-2+4x ; ③ y=-2x+8 ; ④y=4x,
y 随 x 的增大而减少的函数是 .(填写序号)
10.已知一次函数 y x 2 ,当函数值 y 0 时,自变量 x的取值范围在数轴上表示正确
的是__________.
11.根据下表中一次函数的自变量 x 与函数 y 的对应值,可得 p 的值为________.
x -2 0 1
y 3 p 0
12.如图,在 Rt△ABC 中,∠ACB=90°,∠A=15°,AB
的垂直平分线与 AC 交于点 D,与 AB 交于点 E,
连结BD.若AD=12cm,则BC的长为 cm.
13.已知 m 为整数,且一次函数 y (m 4)x m 2的图象不经过第二象限,则m
的值为 。
2
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
14.已知一次函数 y kx b 的图象经过点 A(1,-1),B(-1,3)两点,则 k 0
15.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再
赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x 表示乌龟从起点出发所行
的时间,y1 表示乌龟所行的路程,y2 表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为 1000 米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了 10 分钟;
④兔子在途中 750 米处追上乌龟.
其中正确的说法是 .(把你认为正确说法
的序号都填上)
16. 如图,在△ABC 中,AB=AC,D 为 BC 边上一点,
且∠BAD=30°,若 AD=DE,∠EDC=33°,则∠DAE
的度数为 °.
三、解答题
17.直线 AB 与 x 轴交于点 A(1,0),与 y 轴交于点 B(0,-2).
(1)求直线 AB 的解析式;
S 2
(2)若直线 AB 上一点 C 在第一象限,且 BOC ,求点 C 坐标.
18.如图,D 是等边△ABC 的边 AB 上的一动点,以 CD 为一边向上作等边△EDC,
连接 AE,找出图中的一组全等三角形,并说明理由.
A E
D
B C
3
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
19.如图,把矩形纸片 ABCD 沿 EF 折叠,使点 B 落在边 AD 上的点 B′处,点 A 落
在点 A′处,求证:B′ E=BF。
20.如图,在△ABC中,∠CAB的平分线 AD 与 BC的垂直平分线 DE交于点 D,DM⊥AB
于 M,DN⊥AC交 AC的延长线于 N. 求证:BM=CN .
证明:
A
M
E
B C
N
D
21.(1)如图 1,A、B是直线 l 同旁的两个定点.请你在直线 l 上确定一点 P,使 PA+PB
的值最小.
B
B
A P
l
O A
图1 图2
(2)如图 2,∠AOB=30°,P 是∠AOB 内一点,PO=10.请你在 OA 上找一点 Q,在
OB 上找一点 R,使得△PQR 的周长最小.要求:画出图形,并计算这个最小值
是 。 .
4
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
4
22.如图,直线 4 4y x 4与y轴交于点 A,与直线 y x 交于点 B,且直线
3 5 5
4 4
y x 与 x 轴交于点 C,求 ABC 的面积.
5 5
23.甲乙两人同时登西山,甲、乙两人距地面的高度 y (米)与登山时间 x (分)
之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在 A 地提速时距地面的高度b 为 米.
(2)若乙提速后,乙的速度是甲登山速度的 3倍,请分别求出甲、乙二人登山全过
程中,登山时距地面的高度 y (米)与登山时间 x (分)之间的函数关系式.
(3)登山多长时间时,乙追上了甲?此时乙距 A 地的高度为多少米?
5
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
1
24. 在直角坐标系中,点 A(4,0),点 P(x,y)是直线 y x 3在第一象限
2
的一点.(1)设△OAP 的面积为 S,用含 x的解析式表示 S,写出自变量取值范围.
1
(2)在直线 y x 3求一点 Q,使△OAQ 是以 OA为底的等腰三角形.
2
(3)若第(2)问变为使△OAQ 是等腰三角形,这样的点有几个?
25.将二个全等的 Rt△ABC与 Rt△DBE按图①的方式摆放。其中∠DEB=∠ACB=90°,
∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F。(1)求证:AF+EF=DE;
(2)若将图①中的△DBE 绕 B点按顺时针方向旋转角α,且 0°≤α≤60°,其他了
条件不变,请在图②中画出变换后的图形,并直接写出(1)中的结论是否成立;
(3) 若将图①中的△DBE 绕 B 点按顺时针方向旋转角 β,且 60°≤β≤180°,其
他了条件不变,如图③。你认为(1)中的结论是否成立吗?若成立,写出证明过程,
若不成立,请写出这时 AF、EF和 DE之间的关系,并说明理由。
D
B
E
B B
E
F AC
C A
F C A D
图① 图② 图③
6
{#{QQABYY6UggAgABIAAQhCEwEYCAAQkBAACAoGQBAEIAABSAFABAA=}#}
同课章节目录
