北京市西城区重点中学2023~2024学年下学期八年级开学考数学试卷(pdf版 无答案)
文档属性
| 名称 | 北京市西城区重点中学2023~2024学年下学期八年级开学考数学试卷(pdf版 无答案) |  | |
| 格式 | |||
| 文件大小 | 390.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 09:01:40 | ||
图片预览

文档简介
数学练习 2024.2.29
姓名:______________ 班级:______________
一、选择题(共 24分,每题 3分)第 1-8题均有四个选项,符合题意的选项只有一个.
1. 将数字 0.000 000 5用科学记数法表示应为( )
A 8 7 6 6.50 10 B.5 10 C.5 10 D.0.5 10
2. 下列计算正确的是( )
A a3 a2 2a5 B a2 a3 a6 C (3a3)2 9a6. . . D. a8 a2 a4
3. 1如果二次根式 有意义,那么 x的取值范围是( )
x 3
A. x 3 B. x 3 C. x 3 D. x 3
4. 如图,在△ABC中,∠ABC=50°,∠BAC=20°,D为线段 AB的
垂直平分线与直线 BC的交点,连结 AD,则∠CAD=( )
A.10° B.20°
C.30° D.40°
5. 下列各式中,计算正确的是( )
A.98 102 100 2 100 2 1002 2 9998
x
B. 1 3
x 3 x 3
C. (15x2 y 5xy2 ) 5xy 3x 5y
D. (3x 1)(x 2) 3x2 5x 2
6. 下列各组的两个根式,是同类二次根式的是( )
1 1
A. a和 ab B. 20和 0.2 C. 8ab3 和 2 ab D. 和xy 2xy
7. 如图,∠MAN=30°,点 B是射线 AN上的定点,点 P是直
线 AM上的动点,要使△PAB 为等腰三角形,则满足条件的
点 P 共有( )个.
A. 1 B. 2 C. 3 D. 4
第 1 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
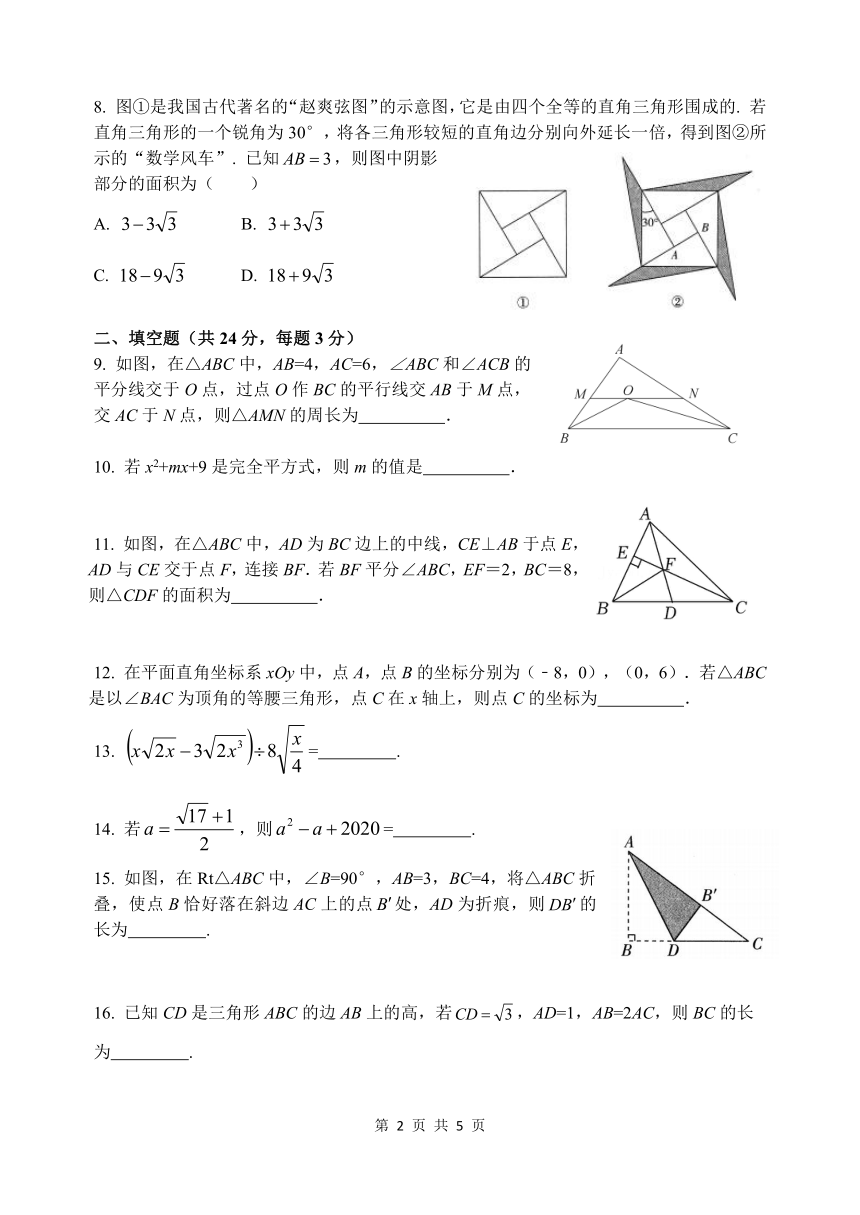
8. 图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的. 若
直角三角形的一个锐角为 30°,将各三角形较短的直角边分别向外延长一倍,得到图②所
示的“数学风车”. 已知 AB 3,则图中阴影
部分的面积为( )
A. 3 3 3 B. 3 3 3
C. 18 9 3 D. 18 9 3
二、填空题(共 24分,每题 3分)
9. 如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的
平分线交于 O点,过点 O作 BC的平行线交 AB于 M点,
交 AC于 N点,则△AMN的周长为 .
10. 若 x2+mx+9是完全平方式,则 m的值是 .
11. 如图,在△ABC中,AD为 BC边上的中线,CE⊥AB于点 E,
AD与 CE交于点 F,连接 BF.若 BF平分∠ABC,EF=2,BC=8,
则△CDF的面积为 .
12. 在平面直角坐标系 xOy中,点 A,点 B的坐标分别为(﹣8,0),(0,6).若△ABC
是以∠BAC为顶角的等腰三角形,点 C在 x轴上,则点 C的坐标为 .
13. x 2x 3 2x3 x 8 = .
4
a 17 114. 2若 ,则 a a 2020 = .
2
15. 如图,在 Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折
叠,使点 B恰好落在斜边 AC上的点 B 处,AD为折痕,则DB 的
长为 .
16. 已知 CD是三角形 ABC的边 AB上的高,若CD 3,AD=1,AB=2AC,则 BC的长
为 .
第 2 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
三、解答题(共 52分,第 17、18、19、20、21、22题每题 6分,第 23、24每题 8分)解答
应写出文字说明、演算步骤或证明过程.
17. 计算:
(1) 12 4 27 (2) 6 2 6 2 52 .
18. 因式分解:(1)3x2﹣6xy+3y2 3 5(2) 4amx am x
2 a 1 a2 1
19. 先化简 2 ,然后从-2,-1,0,1,2中,选择一个合适的数代入a 1 a a 2a
求值.
20. 如图,四边形 ABCD中,AB=AC,∠D=90°,BE⊥AC 于点 F,交 CD于点 E,连
接 EA,EA平分∠DEF.
(1)求证:AF=AD;
(2)若 BF=7,DE=3,求 CE的长.
21. 如图,在等腰 Rt△ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC= 7 ,
求∠CPA的度数.
第 3 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
22. 观察,思考,解答:
( 2 1)2 ( 2)2 2 1 2 12 2 2 2 1 3 2 2 ,
2 2
反之,3 2 2 2 2 2 1 ( 2 1) ,即3 2 2 ( 2 1) .
所以 3 2 2 2 1.
(1)仿照上列,化简 4 2 3 =__________;
1 1 x2 4
(2)已知 x 5 2 6 ,求 2 的值.(结果需化为最简的二次根式) x 2 x 2 2x
23. 已知 AB=BC,∠ABC=90°,直线 l是过点 B的一条动直线(不与直线 AB,BC重合),
分别过点 A,C作直线 l的垂线,垂足为 D,E.
(1)如图 1,当 45 ABD 90 时,
①求证:CE DE AD;
②连接 AE,过点 D作 DH⊥AE于 H,过点 A作 AF∥BC交 DH的延长线于点 F.依题意
补全图形,用等式表示线段 DF,BE,DE的数量关系,并证明;
(2)在直线 l运动的过程中,若 DE的最大值为 3,直接写出 AB的长.
图 1 备用图
第 4 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
24. 在平面直角坐标系 xOy中,直线 l过原点且经过第三、第一象限,l与 x轴所夹锐角为
n°.对于点 P和 x轴上的两点 M,N,给出如下定义:记点 P关于直线 l的对称点为 Q,
若点 Q的纵坐标为正数,且△MNQ为等边三角形,则称点 P为 M,N的 n°点.
(1)如图 1,若点 M(2,0),N(4,0),点 P为 M,N的 45°点,连接 OP,OQ.
①∠POQ= °;
②求点 P坐标.
(2)已知点 M(m,0),N(m+t,0).
①当 t=2时,点 P为 M,N的 60°点,且点 P的横坐标为﹣2,则 m= ;
②当 m=﹣2时,点 P为 M,N的 30°点,且点 P的横坐标为 2,则 t= .
第 5 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
姓名:______________ 班级:______________
一、选择题(共 24分,每题 3分)第 1-8题均有四个选项,符合题意的选项只有一个.
1. 将数字 0.000 000 5用科学记数法表示应为( )
A 8 7 6 6.50 10 B.5 10 C.5 10 D.0.5 10
2. 下列计算正确的是( )
A a3 a2 2a5 B a2 a3 a6 C (3a3)2 9a6. . . D. a8 a2 a4
3. 1如果二次根式 有意义,那么 x的取值范围是( )
x 3
A. x 3 B. x 3 C. x 3 D. x 3
4. 如图,在△ABC中,∠ABC=50°,∠BAC=20°,D为线段 AB的
垂直平分线与直线 BC的交点,连结 AD,则∠CAD=( )
A.10° B.20°
C.30° D.40°
5. 下列各式中,计算正确的是( )
A.98 102 100 2 100 2 1002 2 9998
x
B. 1 3
x 3 x 3
C. (15x2 y 5xy2 ) 5xy 3x 5y
D. (3x 1)(x 2) 3x2 5x 2
6. 下列各组的两个根式,是同类二次根式的是( )
1 1
A. a和 ab B. 20和 0.2 C. 8ab3 和 2 ab D. 和xy 2xy
7. 如图,∠MAN=30°,点 B是射线 AN上的定点,点 P是直
线 AM上的动点,要使△PAB 为等腰三角形,则满足条件的
点 P 共有( )个.
A. 1 B. 2 C. 3 D. 4
第 1 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
8. 图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的. 若
直角三角形的一个锐角为 30°,将各三角形较短的直角边分别向外延长一倍,得到图②所
示的“数学风车”. 已知 AB 3,则图中阴影
部分的面积为( )
A. 3 3 3 B. 3 3 3
C. 18 9 3 D. 18 9 3
二、填空题(共 24分,每题 3分)
9. 如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的
平分线交于 O点,过点 O作 BC的平行线交 AB于 M点,
交 AC于 N点,则△AMN的周长为 .
10. 若 x2+mx+9是完全平方式,则 m的值是 .
11. 如图,在△ABC中,AD为 BC边上的中线,CE⊥AB于点 E,
AD与 CE交于点 F,连接 BF.若 BF平分∠ABC,EF=2,BC=8,
则△CDF的面积为 .
12. 在平面直角坐标系 xOy中,点 A,点 B的坐标分别为(﹣8,0),(0,6).若△ABC
是以∠BAC为顶角的等腰三角形,点 C在 x轴上,则点 C的坐标为 .
13. x 2x 3 2x3 x 8 = .
4
a 17 114. 2若 ,则 a a 2020 = .
2
15. 如图,在 Rt△ABC中,∠B=90°,AB=3,BC=4,将△ABC折
叠,使点 B恰好落在斜边 AC上的点 B 处,AD为折痕,则DB 的
长为 .
16. 已知 CD是三角形 ABC的边 AB上的高,若CD 3,AD=1,AB=2AC,则 BC的长
为 .
第 2 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
三、解答题(共 52分,第 17、18、19、20、21、22题每题 6分,第 23、24每题 8分)解答
应写出文字说明、演算步骤或证明过程.
17. 计算:
(1) 12 4 27 (2) 6 2 6 2 52 .
18. 因式分解:(1)3x2﹣6xy+3y2 3 5(2) 4amx am x
2 a 1 a2 1
19. 先化简 2 ,然后从-2,-1,0,1,2中,选择一个合适的数代入a 1 a a 2a
求值.
20. 如图,四边形 ABCD中,AB=AC,∠D=90°,BE⊥AC 于点 F,交 CD于点 E,连
接 EA,EA平分∠DEF.
(1)求证:AF=AD;
(2)若 BF=7,DE=3,求 CE的长.
21. 如图,在等腰 Rt△ABC中,∠A=90°,P是△ABC内一点,PA=1,PB=3,PC= 7 ,
求∠CPA的度数.
第 3 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
22. 观察,思考,解答:
( 2 1)2 ( 2)2 2 1 2 12 2 2 2 1 3 2 2 ,
2 2
反之,3 2 2 2 2 2 1 ( 2 1) ,即3 2 2 ( 2 1) .
所以 3 2 2 2 1.
(1)仿照上列,化简 4 2 3 =__________;
1 1 x2 4
(2)已知 x 5 2 6 ,求 2 的值.(结果需化为最简的二次根式) x 2 x 2 2x
23. 已知 AB=BC,∠ABC=90°,直线 l是过点 B的一条动直线(不与直线 AB,BC重合),
分别过点 A,C作直线 l的垂线,垂足为 D,E.
(1)如图 1,当 45 ABD 90 时,
①求证:CE DE AD;
②连接 AE,过点 D作 DH⊥AE于 H,过点 A作 AF∥BC交 DH的延长线于点 F.依题意
补全图形,用等式表示线段 DF,BE,DE的数量关系,并证明;
(2)在直线 l运动的过程中,若 DE的最大值为 3,直接写出 AB的长.
图 1 备用图
第 4 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
24. 在平面直角坐标系 xOy中,直线 l过原点且经过第三、第一象限,l与 x轴所夹锐角为
n°.对于点 P和 x轴上的两点 M,N,给出如下定义:记点 P关于直线 l的对称点为 Q,
若点 Q的纵坐标为正数,且△MNQ为等边三角形,则称点 P为 M,N的 n°点.
(1)如图 1,若点 M(2,0),N(4,0),点 P为 M,N的 45°点,连接 OP,OQ.
①∠POQ= °;
②求点 P坐标.
(2)已知点 M(m,0),N(m+t,0).
①当 t=2时,点 P为 M,N的 60°点,且点 P的横坐标为﹣2,则 m= ;
②当 m=﹣2时,点 P为 M,N的 30°点,且点 P的横坐标为 2,则 t= .
第 5 页 共 5 页
{#{QQABYYYQogCgABAAAAgCEwEICgAQkAGAAIoGhAAMIAABCRFABAA=}#}
同课章节目录
