矩形的性质
图片预览



文档简介
课件28张PPT。数学箴言 给我最大快乐的,不是已懂得知识,而是不断的学习;不是已有的东西,而是不断的获取;不是已达到的高度,而是继续不断的攀登.
----高斯 复习提问1.什么叫平行四边形?2. 平行四边形与四边
形有什么关系?两组对边分别平行的四边形叫做平行四边形 .特殊一般 平行四边形
具有四边形的
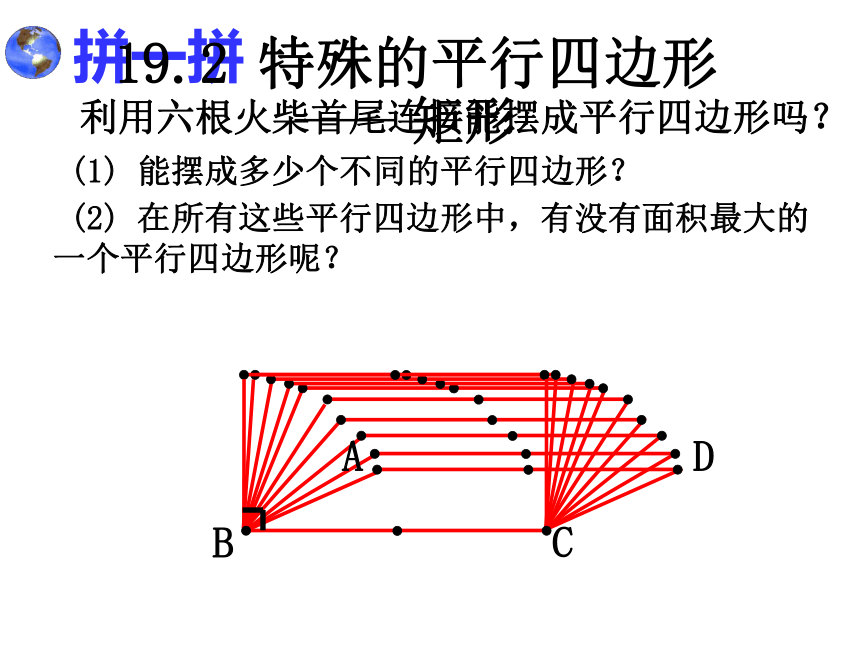
一切性质拼一拼利用六根火柴首尾连接能摆成平行四边形吗? (1) 能摆成多少个不同的平行四边形? (2) 在所有这些平行四边形中,有没有面积最大的
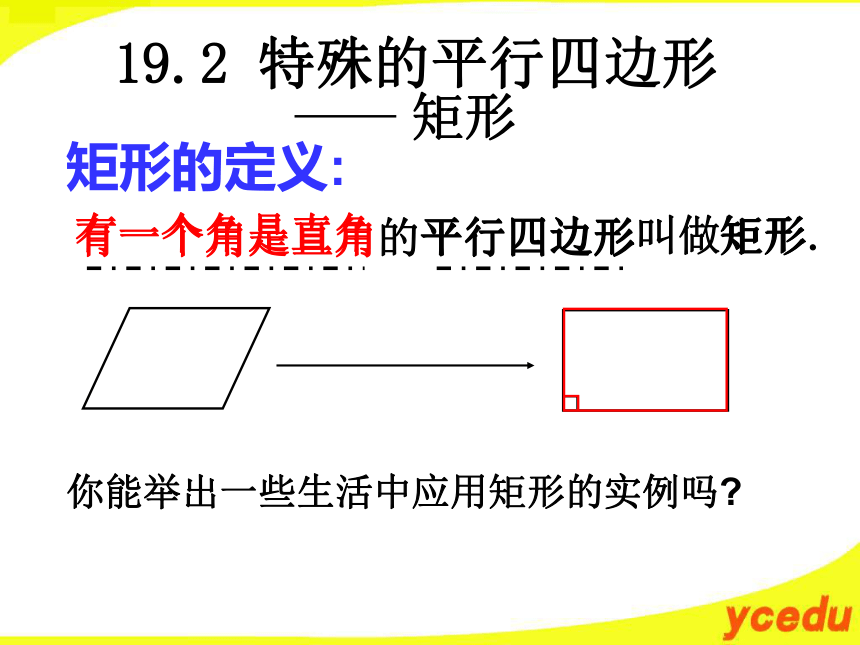
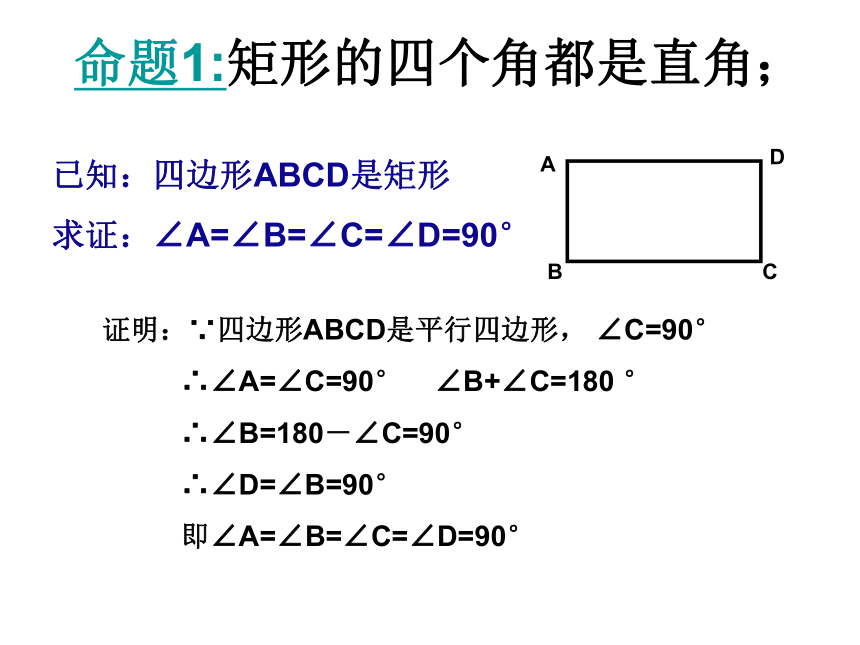
一个平行四边形呢?19.2 特殊的平行四边形平行四边形19.2 特殊的平行四边形 有一个角是直角的平行四边形矩形的定义: 叫做矩形.有一个角是直角矩形 你能举出一些生活中应用矩形的实例吗?矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补矩形是轴对称图形吗?它的对称轴有几条?ABCDEFGH.点燃思维 矩形的四个角都是直角. 性质1: 猜想2:矩形的对角线相等.猜想1:O矩形特殊的性质命题1:矩形的四个角都是直角;已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
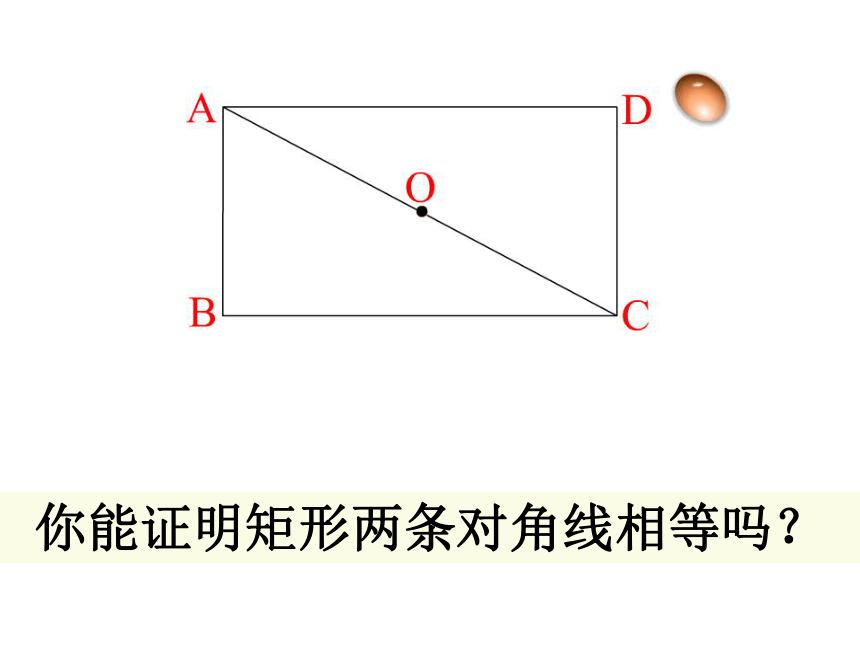
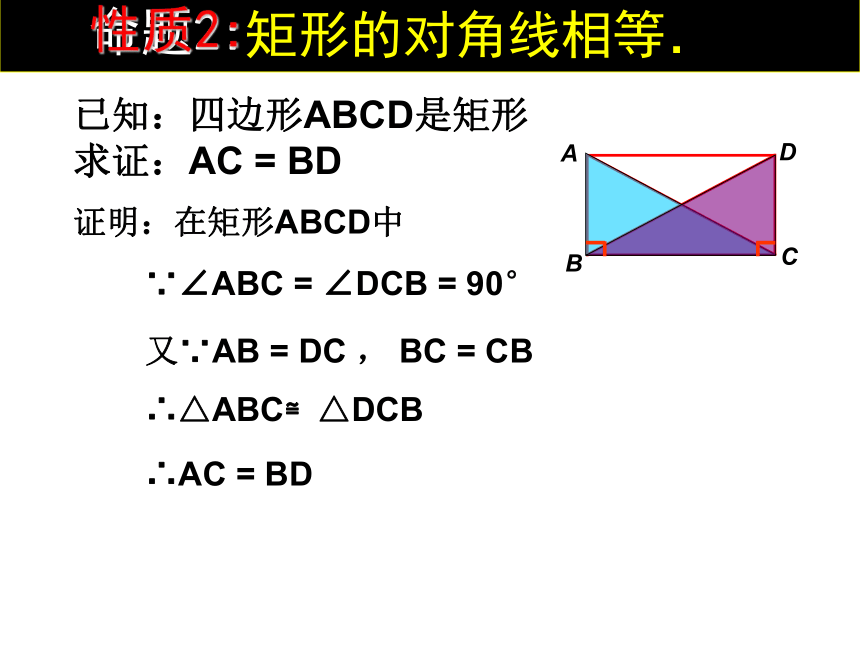
即∠A=∠B=∠C=∠D=90°你能证明矩形两条对角线相等吗?已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 矩形的对角线相等.命题2:性质2:矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:符号语言: ∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900符号语言: ∵四边形ABCD是矩形 ∴AC = BD矩形的性质∠BAD=∠BCD =∠ABC=∠ADC= 90°探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠DOA=OC,OB=OD矩形的四个角都是直角;矩形的对角线相等对角相等;对角线互相平分;且互相平分;OA=OC=OB=OD思维提升既是中心对称图形又是轴对称图形对边平行且
相等四个角都等于
90°对角线互相
平分且相等如图:在矩形ABCD中, 找出相等的线段与相等的角。想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三角形,有几对全等的等腰三角形?牛刀小试方法一:矩形的问题可以转化到直角三角形或等腰(边)三角形中的问题来解决. ODCBA相等的线段:AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ , OB= ㎝.
2 若OA=3㎝,则AC= ㎝.
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝,
矩形的面积= ㎝2.
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝.51012482861.矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等 闯关2.下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直DD3.矩形ABCD中,∠ABD:∠DBC=2:1,
则∠ADB=???????度。若AB=4,则AC=???? 。 ????????????????????????????????????? 4.矩形的边长为10cm和15cm,其中一个
内角的平分线分长边为两部分,这两部
分的长分别为???? cm,????? cm. ?????????????????????????????????308E1231055.如果矩形的一边与对角线的夹角为50o,
则两对角线相交所成的锐角的度数 为?? ??????????度。??????????? ???????????????????????????????????????????????????????????????????? ? 50080寓学于乐 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗?公平,OB= OA=OCBO = AC推论:直角三角形斜边上的中线等于斜边的一半.D已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = ACD证明: 延长BO至D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD ∴四边形ABCD是平行四边形.∴AC=BD∵ ∠ABC=900推论:直角三角形斜边上的中线等于斜边的一半.回 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O方法二: 如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形. AB=OA=4cm, 已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°, AB=4cm,例题赏析求矩形对角线的长.求∠AOD的度数.1.在矩形ABCD中,若AB = 3,BC = 4,则它的面积
是_____.AC =____. BD =____.
2.在矩形ABCD中, ∠ACB=30°,AB = 3,则AC =
____ ,BD =____. ∠AOB =____ ,∠BOC =______.
12556660°120°学以致用5.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D6.已知MN//PQ,直线L分别交MN、PQ于
点A、C,同旁内角的平分线AB、BC相交于
点B,AD、CD相交于点D,
证明:四边形ABCD是矩形。MNPQABCD1234 某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.(1)圈出的空地是什么形状? (2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗?若能,则喷水器应安放在何处;若不能,请说明理由.O6868课堂小结1.知识小结2.学法小结(1)用类比的方法探究矩形的性质,先找共性再找特殊性,
并注意性质的整合;(2)矩形的问题常可以转化为直角三角形或等腰三角形
的问题来解决.课后作业课本P113页习题19.2第3题
思考题:如图:矩形ABCD,AB长8cm,对角 线比AD边长4cm.求AD的长及点A到BD的距离AE的长.
----高斯 复习提问1.什么叫平行四边形?2. 平行四边形与四边
形有什么关系?两组对边分别平行的四边形叫做平行四边形 .特殊一般 平行四边形
具有四边形的
一切性质拼一拼利用六根火柴首尾连接能摆成平行四边形吗? (1) 能摆成多少个不同的平行四边形? (2) 在所有这些平行四边形中,有没有面积最大的
一个平行四边形呢?19.2 特殊的平行四边形平行四边形19.2 特殊的平行四边形 有一个角是直角的平行四边形矩形的定义: 叫做矩形.有一个角是直角矩形 你能举出一些生活中应用矩形的实例吗?矩形的性质的研究:我们已经知道矩形是特殊的平行四边形,因此矩形除具有平行四边形的性质外,还有它的特殊性质.你能说出矩形有哪些性质吗?四、矩形 两条对角线互相平分三、矩形的两组对角分别相等二、矩形的两组对边分别相等一、矩形的两组对边分别平行五、矩形的邻角互补矩形是轴对称图形吗?它的对称轴有几条?ABCDEFGH.点燃思维 矩形的四个角都是直角. 性质1: 猜想2:矩形的对角线相等.猜想1:O矩形特殊的性质命题1:矩形的四个角都是直角;已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°证明:∵四边形ABCD是平行四边形, ∠C=90°
∴∠A=∠C=90° ∠B+∠C=180 °
∴∠B=180-∠C=90°
∴∠D=∠B=90°
即∠A=∠B=∠C=∠D=90°你能证明矩形两条对角线相等吗?已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD 矩形的对角线相等.命题2:性质2:矩形特殊的性质矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:符号语言: ∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900符号语言: ∵四边形ABCD是矩形 ∴AC = BD矩形的性质∠BAD=∠BCD =∠ABC=∠ADC= 90°探究矩形的性质O(1)对边平行且相等;(2) (3)∠A=∠C , ∠B=∠DOA=OC,OB=OD矩形的四个角都是直角;矩形的对角线相等对角相等;对角线互相平分;且互相平分;OA=OC=OB=OD思维提升既是中心对称图形又是轴对称图形对边平行且
相等四个角都等于
90°对角线互相
平分且相等如图:在矩形ABCD中, 找出相等的线段与相等的角。想一想:上图中有几个直角三角形,它们全等吗?图中有个等腰三角形,有几对全等的等腰三角形?牛刀小试方法一:矩形的问题可以转化到直角三角形或等腰(边)三角形中的问题来解决. ODCBA相等的线段:AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD相等的角:∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB等腰三角形有:△OAB △ OBC △OCD △OAD直角三角形有:Rt△ABC Rt△BCD Rt△CDA Rt△DAB全等三角形有:Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB已知四边形ABCD是矩形如图:四边形ABCD是矩形
若已知AB=8㎝,AD=6㎝,
则AC= ㎝ , OB= ㎝.
2 若OA=3㎝,则AC= ㎝.
若已知AC=10㎝,BC=6㎝,则矩形的周长= ㎝,
矩形的面积= ㎝2.
4 若已知 ∠DOC=120°,AD=6㎝,则AC= ㎝.51012482861.矩形具有而平行四边形不具有的性质( )
(A)内角和是360度 (B)对角相等
(C)对边平行且相等 (D)对角线相等 闯关2.下面性质中,矩形不一定具有的是( )
(A)对角线相等 (B)四个角相等
(C)是轴对称图形 (D)对角线垂直DD3.矩形ABCD中,∠ABD:∠DBC=2:1,
则∠ADB=???????度。若AB=4,则AC=???? 。 ????????????????????????????????????? 4.矩形的边长为10cm和15cm,其中一个
内角的平分线分长边为两部分,这两部
分的长分别为???? cm,????? cm. ?????????????????????????????????308E1231055.如果矩形的一边与对角线的夹角为50o,
则两对角线相交所成的锐角的度数 为?? ??????????度。??????????? ???????????????????????????????????????????????????????????????????? ? 50080寓学于乐 三位学生正在做投圈游戏,他们分别站在一个直角三角形的三个顶点处,目标物放在斜边的中点处,这样的队形对每个人公平吗?公平,OB= OA=OCBO = AC推论:直角三角形斜边上的中线等于斜边的一半.D已知:在Rt△ABC中,∠ABC=900,BO是AC上的中线.
求证: BO = ACD证明: 延长BO至D,使OD=BO,
连结AD、DC.∵AO=OC, BO=OD ∴四边形ABCD是平行四边形.∴AC=BD∵ ∠ABC=900推论:直角三角形斜边上的中线等于斜边的一半.回 解:∵ 四边形ABCD是矩形
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4(㎝)
∴ 矩形的对角线长 AC=BD=2OA=8(㎝)O方法二: 如果矩形两对角线的夹角是60°或120°, 则其中必有等边三角形. AB=OA=4cm, 已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°, AB=4cm,例题赏析求矩形对角线的长.求∠AOD的度数.1.在矩形ABCD中,若AB = 3,BC = 4,则它的面积
是_____.AC =____. BD =____.
2.在矩形ABCD中, ∠ACB=30°,AB = 3,则AC =
____ ,BD =____. ∠AOB =____ ,∠BOC =______.
12556660°120°学以致用5.如图,用8块相同的长方形地砖拼成一个矩形地面,则每块长方形地砖的长和宽分别是( )
(A)48cm,12cm; (B)48cm,16cm;
(C)44cm,16cm; (D)45cm,15cm.D6.已知MN//PQ,直线L分别交MN、PQ于
点A、C,同旁内角的平分线AB、BC相交于
点B,AD、CD相交于点D,
证明:四边形ABCD是矩形。MNPQABCD1234 某学校因地制宜:先向北量6m,再向东量8m,接着向南量6m,最后向西量8m,在圈出的这块空地上建一个草坪.(1)圈出的空地是什么形状? (2)考虑到护理草坪,学校购置了一台自动喷水器, 这台机器的最大喷水距离为5m,问这台机器能对整个草坪进行护理吗?若能,则喷水器应安放在何处;若不能,请说明理由.O6868课堂小结1.知识小结2.学法小结(1)用类比的方法探究矩形的性质,先找共性再找特殊性,
并注意性质的整合;(2)矩形的问题常可以转化为直角三角形或等腰三角形
的问题来解决.课后作业课本P113页习题19.2第3题
思考题:如图:矩形ABCD,AB长8cm,对角 线比AD边长4cm.求AD的长及点A到BD的距离AE的长.
