北师大版七年级数学下册尖子生培优必刷题 专题2.4相交线大题专练(重难点培优30题)(原卷版+解析版)
文档属性
| 名称 | 北师大版七年级数学下册尖子生培优必刷题 专题2.4相交线大题专练(重难点培优30题)(原卷版+解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 808.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 00:00:00 | ||
图片预览


文档简介
专题2.4相交线大题专练(重难点培优30题)
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、解答题
1.(黑龙江省哈尔滨市南岗区第六十九中学2022-2023学年度七年级上学期期中学业水平检测数学(五四制)试卷)如图,直线、相交于点,平分,,,求的度数.
2.(广东省东莞市石龙第二中学2021-2022学年七年级下学期期中数学试卷)如图,直线,相交于,是的角平分线.
(1)的对顶角是 ___________;
(2)若,求、的度数.
3.(黑龙江省哈尔滨德强学校2022—2023学年七年级上学期11月份线上教学问题诊断数学试题)如图,直线、相交于点,平分,垂足为点,且.
(1)如图,求的度数.
(2)在不添加任何辅助线的情况下,请直接写出图中与互余的角.
4.(2023秋·陕西延安·七年级统考期末)如图,点 A 、O 、B 在同一直线上,平分,若.
(1)求的度数;
(2)若平分,求的度数.
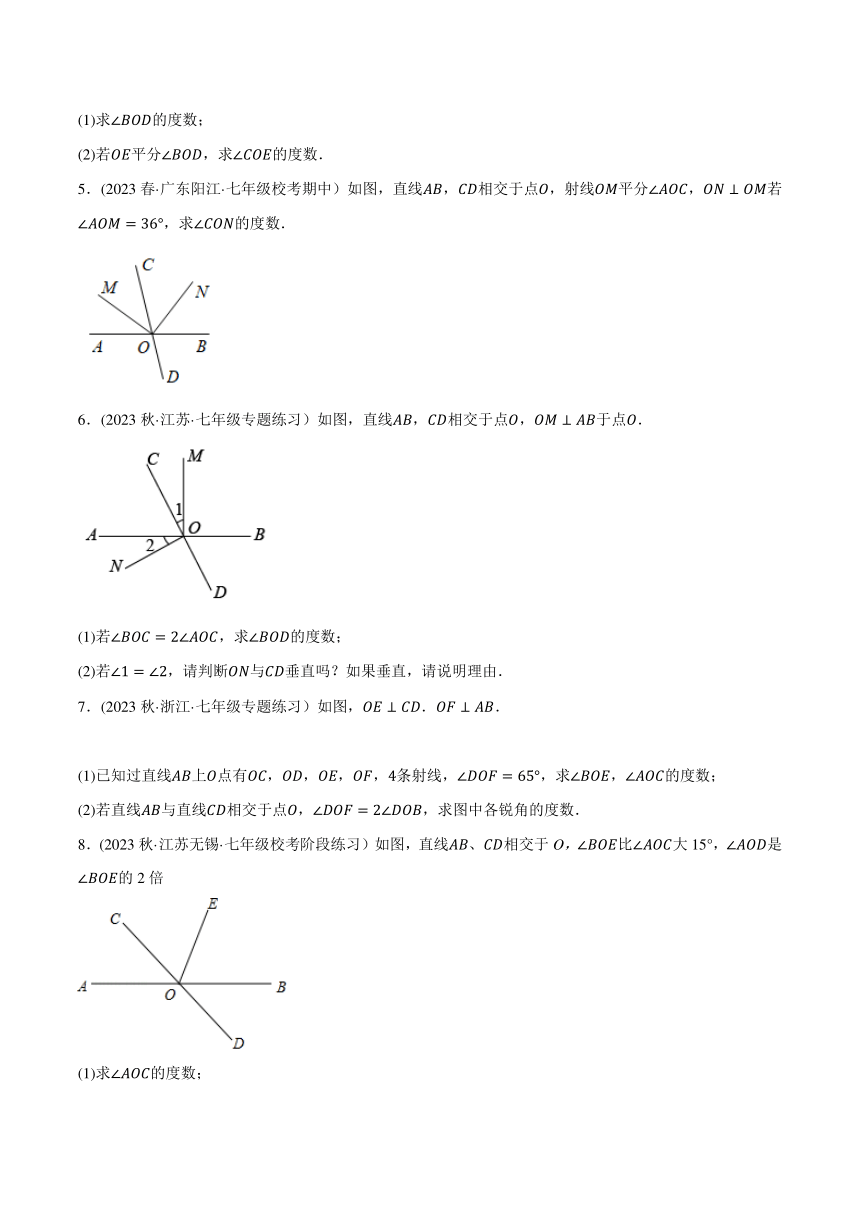
5.(2023春·广东阳江·七年级校考期中)如图,直线,相交于点,射线平分,若,求的度数.
6.(2023秋·江苏·七年级专题练习)如图,直线相交于点,于点.
(1)若,求的度数;
(2)若,请判断与垂直吗?如果垂直,请说明理由.
7.(2023秋·浙江·七年级专题练习)如图,.
(1)已知过直线上点有,条射线,,求的度数;
(2)若直线与直线相交于点,求图中各锐角的度数.
8.(2023秋·江苏无锡·七年级校考阶段练习)如图,直线相交于O,比大15°,是的2倍
(1)求的度数;
(2)试说明平分.
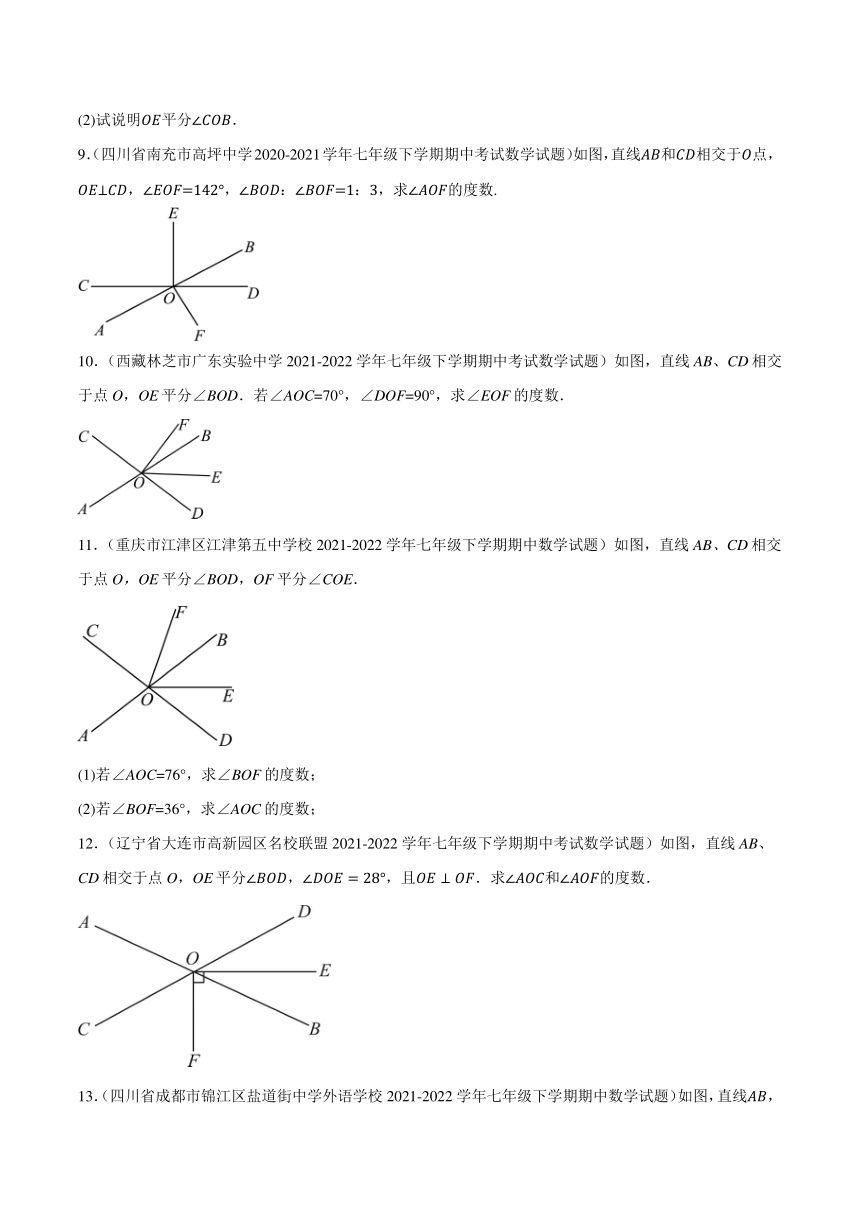
9.(四川省南充市高坪中学2020-2021学年七年级下学期期中考试数学试题)如图,直线和相交于点,,,,求的度数.
10.(西藏林芝市广东实验中学2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD.若∠AOC=70°,∠DOF=90°,求∠EOF的度数.
11.(重庆市江津区江津第五中学校2021-2022学年七年级下学期期中数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
12.(辽宁省大连市高新园区名校联盟2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分,,且.求和的度数.
13.(四川省成都市锦江区盐道街中学外语学校2021-2022学年七年级下学期期中数学试题)如图,直线,相交于点,平分.
(1)若,,求的度数;
(2)若平分,,求的度数.
14.(广东省广州市白云区六校2021-2022学年下学期七年级期中数学试卷-)如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.
(1)求∠AOF的度数.
(2)判断OE与OF的位置关系并说明理由.
15.(广东省惠州市大亚湾第三中学2021--2022学年七年级下学期数学期中考试试卷)如图,直线,相交于点,,垂足为.若,求的度数.
16.(福建省长汀县第四中学2021-2022学年七年级下学期第一次适应性练习数学试题)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
17.(广东省东莞市松山湖实验中学2020-2021学年七年级下学期期中数学试卷)如图,直线与相交于点,于点,平分,且,求的度数.
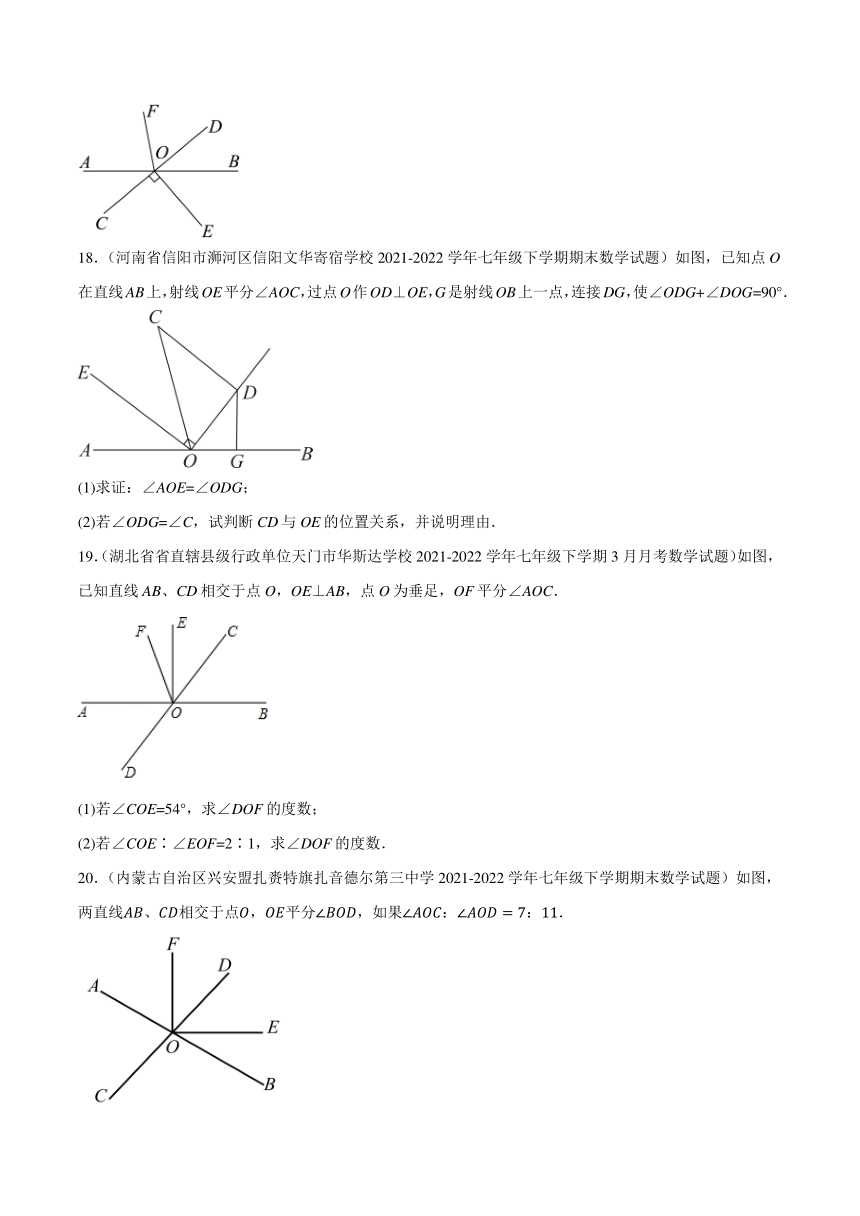
18.(河南省信阳市浉河区信阳文华寄宿学校2021-2022学年七年级下学期期末数学试题)如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
19.(湖北省省直辖县级行政单位天门市华斯达学校2021-2022学年七年级下学期3月月考数学试题)如图,已知直线AB、CD相交于点O,OE⊥AB,点O为垂足,OF平分∠AOC.
(1)若∠COE=54°,求∠DOF的度数;
(2)若∠COE∶∠EOF=2∶1,求∠DOF的度数.
20.(内蒙古自治区兴安盟扎赉特旗扎音德尔第三中学2021-2022学年七年级下学期期末数学试题)如图,两直线、相交于点,平分,如果::.
(1)求;
(2)若,,求.
21.(福建省建宁县城关中学片区2021-2022学年七年级下学期第一次单元检测(月考)数学试题)如图,直线相交于点O,平分,求:
(1)的度数;
(2)写出图中互余的角;
(3)的度数.
22.(河北省保定市满城区龙门中学2021-2022学年七年级下学期期末教学质量监测数学试题)如图,直线,相交于点,于点.
(1)若,求的度数;
(2)若,求的度数.
23.(浙江省丽水市莲都区2021-2022学年七年级上学期期末数学试题)如图,直线AE与CD相交于点B,BF⊥AE.
(1)若∠DBE=60°,求∠FBD的度数;
(2)猜想∠CBE与∠DBF的数量关系,并说明理由.
24.(广西壮族自治区百色市靖西市2021-2022学年七年级下学期期末数学试题)如图,直线AB、CD相交于点O,∠AOC=60°,射线OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
(1)求∠BOE的度数.
(2)过点O作射线OF⊥OE,求∠DOF的度数.
25.(2023秋·河北石家庄·七年级石家庄市第九中学校考期末)已知:O 是直线上的一点,是直角,平分钝角.
(1)如图 1,若,求的度数;
(2)如图 2,平分,求的度数;
(3)当时,绕点 O 以每秒 5°沿逆时针方向旋转 t 秒(),请直接写出和之间的数量关系.
26.(2023秋·河北石家庄·七年级石家庄市第四十一中学校考期末)如图,将两块直角三角板的直角顶点C叠放在一起.
(1) ______(填“”“”或“”);
(2)当时,求的度数;
(3)猜想与的数量关系,并说明理由;
(4)将三角板绕点C逆时针旋转一周,请直接写出此时为多少度时,与的大小是二倍关系.
27.(2023秋·安徽·七年级统考期末)如图,点是直线上的一点,,平分.
(1)如图1,若,则______°,______°.
(2)如图2,射线和分别位于直线的两侧,若,求的度数;
(3)如图3,射线和位于直线的下侧,求的度数.
28.(江西省抚州市实验学校2021-2022学年七年级下学期数学第一阶段综合练习题)如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且.请回答下列问题:
(1)∠AOE度数是 ;∠DOE度数是 ;
(2)将射线OE绕点O逆时针旋转α°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,OB是否平分∠DOF?请说明其理由;
②当OA⊥OF时,请求出α的度数.
29.(辽宁省沈阳市沈河区第七中学2022-2023学年七年级上学期期中数学试题)【实践操作】三角尺中的数学.
(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,.
①若,则______;若,则_____;
②猜想:请直接写出与的数量关系:_______.
(2)如图乙若是两个同样的直角三角尺60°锐角的顶点虫重合在一起,,则请直接写出与的数量关系______;
(3)已知,(、都是锐角),如图3,若把它们的顶点O重合在一起,请直接写出与的数量关系: _______.
30.(云南省红河哈尼族彝族自治州建水县2021-2022学年七年级上学期期末数学试题)如图1,点为直线上一点,过点作射线,使.将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点处逆时针旋转至图2,使一边在的内部.且恰好平分,求的度数;
(2)在图3中,延长线段得到射线,判断是否平分,请说明理由.
(3)将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角,则的值为______.(直接写出答案)
专题2.4相交线大题专练(重难点培优30题)
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、解答题
1.(黑龙江省哈尔滨市南岗区第六十九中学2022-2023学年度七年级上学期期中学业水平检测数学(五四制)试卷)如图,直线、相交于点,平分,,,求的度数.
【答案】
【分析】依据,,可得,再根据平分,即可得出,依据平角定义得到.
【详解】解:∵,
∴.
∵.
∴.
∵平分.
∴.
∴.
∵
∴.
【点睛】本题主要考查了垂线的意义,角平分线的定义以及余角的综合运用,正确的识别图形是解题的关键.
2.(广东省东莞市石龙第二中学2021-2022学年七年级下学期期中数学试卷)如图,直线,相交于,是的角平分线.
(1)的对顶角是 ___________;
(2)若,求、的度数.
【答案】(1)
(2),
【分析】(1)根据对顶角定义直接解答即可;
(2)由邻补角定义求出的度数,再根据角平分线定义求出,即可得到的度数.
【详解】(1)解:由对顶角的定义可知,的对顶角是,
故答案为:;
(2),,
,
又是的角平分线.
,
,
答:的度数为.
【点睛】此题考查了几何图形中角度的计算,角平分线的定义,邻补角定义,对顶角定义,正确理解各定义并理解图形中各角的位置关系及数量关系是解题的关键.
3.(黑龙江省哈尔滨德强学校2022—2023学年七年级上学期11月份线上教学问题诊断数学试题)如图,直线、相交于点,平分,垂足为点,且.
(1)如图,求的度数.
(2)在不添加任何辅助线的情况下,请直接写出图中与互余的角.
【答案】(1)
(2)
【分析】(1)先根据垂直的定义得到,再根据平角的定义得到,再根据角平分线的定义得到则,据此求出,即可利用平角的定义求出;
(2)根据余角的定义进行推理即可.
【详解】(1)解:∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∵,
∴,
∵∵平分,
∴,
∴,
∴的余角有.
【点睛】本题主要考查了垂直的定义,角平分线的定义,余角的定义,平角的定义,熟知相关知识是解题的关键.
4.(2023秋·陕西延安·七年级统考期末)如图,点 A 、O 、B 在同一直线上,平分,若.
(1)求的度数;
(2)若平分,求的度数.
【答案】(1)
(2)
【分析】(1)根据平角的定义、角平分线的定义求出,结合图形计算得到答案;
(2)根据角平分线的定义求出∠DOE,结合图形计算得到答案.
【详解】(1)解:∵点A、O、B在同一直线上,平分,
∴,
∴;
(2)解:∵平分,
∴,
∴.
【点睛】本题考查的是角的计算、角平分线的定义,从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
5.(2023春·广东阳江·七年级校考期中)如图,直线,相交于点,射线平分,若,求的度数.
【答案】
【分析】首先根据角平分线的定义可求得的度数,由垂线的定义可知,故此可求得的度数.
【详解】∵平分,
∴,
∵,
∴,
∴.
【点睛】本题考查了角平分线的定义和垂线的定义,掌握此定义是解题的关键.
6.(2023秋·江苏·七年级专题练习)如图,直线相交于点,于点.
(1)若,求的度数;
(2)若,请判断与垂直吗?如果垂直,请说明理由.
【答案】(1)
(2)垂直,理由见解析
【分析】(1)根据和平角的定义计算即可;
(2)利用等量代换,可计算出,即可证明出与垂直.
【详解】(1)解:,
,
,
,
直线相交于点,
,
故的度数为:;
(2)解:垂直,
理由如下:
,
,
,
,
,
故与垂直.
【点睛】本题考查了垂直、对顶角、等量代换等知识点,解题的关键是理解垂直、对顶角的定义.
7.(2023秋·浙江·七年级专题练习)如图,.
(1)已知过直线上点有,条射线,,求的度数;
(2)若直线与直线相交于点,求图中各锐角的度数.
【答案】(1)
(2)图中各锐角的度数为
【分析】(1)根据得出,根据图形可得,,,即可求解;
(2)根据,得出,进而即可求解.
【详解】(1)解:∵,
∴,
∵,
∴,
∴,.
∴;
(2)解:∵,
∴,
∴,
∴,
∴,
∴.
∴图中各锐角的度数为.
【点睛】本题考查了垂线、对顶角、邻补角,解决本题的关键是掌握垂线、对顶角、邻补角定义.
8.(2023秋·江苏无锡·七年级校考阶段练习)如图,直线相交于O,比大15°,是的2倍
(1)求的度数;
(2)试说明平分.
【答案】(1)50°
(2)见解析
【分析】(1)设的度数为x,则,根据平角的定义可得,解方程即可得到答案;
(2)根据(1)所求得到,根据平角的定义求出则,由此即可证明结论.
【详解】(1)解:设的度数为x,
由题意得:,
∵直线相交于O,
∴,
∴,
∴,
∴;
(2)证明:由(1)得:,
∴,
∴,即平分.
【点睛】本题主要考查了几何中角度的计算,一元一次方程的应用,正确理清角之间的关系是解题的关键.
9.(四川省南充市高坪中学2020-2021学年七年级下学期期中考试数学试题)如图,直线和相交于点,,,,求的度数.
【答案】
【分析】根据,得出,根据,可得,根据角的倍分关系,可得∠的度数,根据是邻补角,可得答案.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
∴.
【点睛】本题考查垂直的性质、角的和差、角的倍分关系、邻补角的性质等知识,是基础考点,掌握相关知识是解题关键.
10.(西藏林芝市广东实验中学2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD.若∠AOC=70°,∠DOF=90°,求∠EOF的度数.
【答案】55°
【分析】根据对顶角和角平分线的定义求出∠BOE的度数,再根据已知求出∠BOF的度数,即可求出∠EOF的度数.
【详解】解:∵∠AOC=70°,
∴∠BOD=∠AOC=70°,
∵OE平分∠BOD,
∴∠BOE=∠DOE=∠BOD=35°,
又∵∠DOF=90°,
∴
∴.
【点睛】本题考查角平分线、对顶角,角的和差运算,掌握角平分线的定义,理解对顶角相等是正确解答的关键.
11.(重庆市江津区江津第五中学校2021-2022学年七年级下学期期中数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
【答案】(1)∠BOF=33°
(2)∠AOC=72°
【分析】(1)先根据对顶角相等求出∠BOD=76°,再由角平分线定义得∠DOE=∠BOE=38°,由邻补角得∠COE=142°,再根据角平分线定义得∠EOF=71°,从而可得结论.
(2)利用角平分的定义得出,进而表示出各角求出答案.
【详解】(1)∵∠AOC、∠BOD是对顶角,
∴∠BOD=∠AOC=76°,
∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD=38°
∴∠COE=142°,
∵OF平分∠COE.
∴∠EOF=∠COE=71°,
又∠BOE+∠BOF=∠EOF,
∴∠BOF=∠EOF ∠BOE=71° 38°=33°,
(2)∵OE平分∠BOD,OF平分∠COE,
∴,
∴设,则,
故,,
则,
解得,
故∠AOC=72°.
【点睛】本题考查了角平分线的定义和对顶角的性质,解决本题的关键是掌握对顶角的定义(从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线).
12.(辽宁省大连市高新园区名校联盟2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分,,且.求和的度数.
【答案】,
【分析】根据题意和角平分线的性质得,根据对顶角相等可得,根据得,可得,即可得.
【详解】解:∵OE平分,,
∴,
又∵,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查了角平分线,对顶角,邻补角,解题的关键是掌握角平分线的性质,对顶角相等并认真计算.
13.(四川省成都市锦江区盐道街中学外语学校2021-2022学年七年级下学期期中数学试题)如图,直线,相交于点,平分.
(1)若,,求的度数;
(2)若平分,,求的度数.
【答案】(1)70°
(2)50°
【分析】(1)根据角平分线的性质可得,根据垂线的定义以及已知条件求得,继而求得,根据对顶角相等即可求解;
(2)根据角平分线的性质可得,,设,则,根据平角的定义建立方程,解方程即可求解.
【详解】(1)解:平分,
,
,,
,
,
∴
;
(2)平分,
,
,
设,则,
,
解得:,
故的度数为:.
【点睛】本题考查了几何图形中角度的计算,角平分线的定义,垂线的定义,一元一次方程的应用,数形结合是解题的关键.
14.(广东省广州市白云区六校2021-2022学年下学期七年级期中数学试卷-)如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.
(1)求∠AOF的度数.
(2)判断OE与OF的位置关系并说明理由.
【答案】(1)108°
(2),理由见解析
【分析】(1)设∠1=x°,则∠2=4x°,求出,,根据∠BOC+∠BOD=180°,求出x=18,代入∠AOF=∠AOC+∠COF求出即可.
(2)根据(1)的结论得出,即可求解.
(1)
解:设∠1=x°,则∠2=4x°,
∵OE平分∠BOD,OF平分∠BOC,
∴,
∵∠BOC+∠BOD=180°,
∴8x+2x=180,
∴x=18,
∴∠AOC=∠DOB=2x=36°,∠1=18°,∠2=72°,
∴∠AOF=∠AOC+∠2=36°+72°=108°.
(2)
由(1)可得∠1=18°,∠2=72°,
∴,
∴.
【点睛】本题考查了几何图形中角度的计算,角平分线的定义,数形结合是解题的关键.
15.(广东省惠州市大亚湾第三中学2021--2022学年七年级下学期数学期中考试试卷)如图,直线,相交于点,,垂足为.若,求的度数.
【答案】150°
【分析】由EO⊥AB可得∠BOE=90°,由,,可得∠AOC,从而可得∠BOD,这样由∠DOE=∠BOE+∠BOD即可求得∠DOE的度数.
【详解】解:,,
,
,
,
答:的度数为.
【点睛】本题考查了垂线、对顶角、邻补角,求出∠AOC的度数是解题的关键.
16.(福建省长汀县第四中学2021-2022学年七年级下学期第一次适应性练习数学试题)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
【答案】(1)OF⊥OD,理由见解析;
(2)∠EOF=60°
【分析】(1)利用角平分线的定义结合已知求出∠FOD=90°即可得出答案;
(2)求出∠AOC的度数,再利用对顶角的性质和角平分线的定义求出∠BOD=∠AOC=∠EOD=30°,进而得出∠EOF的度数.
(1)
解:OF⊥OD,
理由:∵OF平分∠AOE,
∴∠AOF=∠FOE,
∵∠DOE=∠BOD,
∴∠AOF+∠BOD=∠FOE+∠DOE=×180°=90°,即∠FOD=90°,
∴OF与OD的位置关系是OF⊥OD;
(2)
∵∠AOC:∠AOD=1:5,
∴∠AOC=×180°=30°,
∴∠BOD=∠AOC=∠EOD=30°,
∴∠AOE=120°,
∴∠EOF=∠AOE=60°.
【点睛】此题主要考查了角平分线的定义以及邻补角的性质,正确得出各角之间的关系是解题关键.
17.(广东省东莞市松山湖实验中学2020-2021学年七年级下学期期中数学试卷)如图,直线与相交于点,于点,平分,且,求的度数.
【答案】70°
【分析】根据垂直的定义,求得,根据,以及对顶角相等可得,然后根据角平分线的定义即可求解.
【详解】,,
,
,
,
又平分,
.
【点睛】本题考查了垂线的定义,几何图形中角度的计算,对顶角相等,角平分线的定义,数形结合求得是解题的关键.
18.(河南省信阳市浉河区信阳文华寄宿学校2021-2022学年七年级下学期期末数学试题)如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
【答案】(1)证明见解析
(2)CDOE,理由见解析
【分析】(1)由OD⊥OE得到∠EOC+∠COD=∠AOE+∠DOG=90°,再利用等角的余角相等即可证明∠AOE=∠ODG;
(2)证明∠EOC=∠C,利用内错角相等两直线平行,即可证明CDOE.
【详解】(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
【点睛】本题考查了角平分线定义,垂直的定义,平行线的判定,等角的余角相等,正确识图是解题的关键.
19.(湖北省省直辖县级行政单位天门市华斯达学校2021-2022学年七年级下学期3月月考数学试题)如图,已知直线AB、CD相交于点O,OE⊥AB,点O为垂足,OF平分∠AOC.
(1)若∠COE=54°,求∠DOF的度数;
(2)若∠COE∶∠EOF=2∶1,求∠DOF的度数.
【答案】(1)∠DOF=108°;
(2)∠DOF=112.5°.
【分析】(1)先由OE⊥AB得出∠AOE=∠BOE=90°,再根据角平分线定义求出∠COF=72°,然后由∠DOF=180°-∠COF即可求解;
(2)设∠EOF=x°,则∠COE=2x°,则∠COF=3x°,再根据角平分线定义求出∠AOF=∠COF=3x°,所以∠AOE=4x°,由垂直的定义可知∠AOE=90°,则4x=90,解之,求出x即可.
【详解】(1)解:∵OE⊥AB,
∴∠AOE=90°;
∵∠COE=54°,
∴∠AOC=∠AOE+∠COE=144°,
∵OF平分∠AOC,
∴∠COF=∠AOC=72°,
∴∠DOF=180°-∠COF=108°;
(2)解:设∠EOF=x°,则∠COE=2x°,
∴∠COF=3x°,
∵OF平分∠AOC,
∴∠AOF=∠COF=3x°,
∴∠AOE=4x°,
∵OE⊥AB,
∴∠AOE=90°,
∴4x=90,解得x=22.5,
∴∠COF=3x°=67.5°,
∴∠DOF=180°-∠COF=112.5°.
【点睛】本题考查了角的计算,根据垂直的定义、角的和差关系列方程进行求解,即可计算出答案,难度适中.
20.(内蒙古自治区兴安盟扎赉特旗扎音德尔第三中学2021-2022学年七年级下学期期末数学试题)如图,两直线、相交于点,平分,如果::.
(1)求;
(2)若,,求.
【答案】(1)145°
(2)125°
【分析】(1)根据邻补角的性质和已知求出和的度数,根据对顶角相等求出和的度数,根据角平分线的定义求出的度数,可以得到的度数;
(2)根据垂直的定义得到,根据互余的性质求出的度数,计算得到答案.
【详解】(1)解:,::,
,,
,,
平分,
,
.
(2)解:,
,
平分,
,
,
.
【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.
21.(福建省建宁县城关中学片区2021-2022学年七年级下学期第一次单元检测(月考)数学试题)如图,直线相交于点O,平分,求:
(1)的度数;
(2)写出图中互余的角;
(3)的度数.
【答案】(1)70°
(2)∠BOF与∠BOD互余,∠EOF与∠EOD互余,∠EOF与∠BOE互余,∠BOF与∠AOC互余
(3)55°
【分析】(1)根据对顶角相等即可得到;
(2)根据余角的定义求解即可;
(3)先根据角平分线的定义求出∠DOE=35°,则∠EOF=∠DOF-∠DOE=55°.
【详解】(1)解:由题意得;
(2)解:∵∠COF=90°,
∴∠DOF=180°-∠COF=90°,
∴∠BOF+∠BOD=90°,∠EOF+∠EOD=90°,
∵OE平分∠BOD,
∴∠BOE=∠DOE,
∴∠EOF+∠BOE=90°,
∵∠AOC=∠BOD,
∴∠BOF+∠AOC=90°,
∴∠BOF与∠BOD互余,∠EOF与∠EOD互余,∠EOF与∠BOE互余,∠BOF与∠AOC互余;
(3)解:∵∠BOD=70°,OE平分∠BOD,
∴∠DOE=35°,
∴∠EOF=∠DOF-∠DOE=55°.
【点睛】本题主要考查了几何中角度的计算,角平分线的定义,对顶角相等,余角的定义,熟知相关知识是解题的关键.
22.(河北省保定市满城区龙门中学2021-2022学年七年级下学期期末教学质量监测数学试题)如图,直线,相交于点,于点.
(1)若,求的度数;
(2)若,求的度数.
【答案】(1)54°
(2)120°
【分析】(1)先由垂直的定义得到∠EOD=90°,再由对顶角相等得到∠BOD=∠AOC=36°,由此求解即可;
(2)根据平角的定义结合已知条件求出∠BOD的度数,进而求出∠BOE的度数,最后根据平角的定义即可求出∠AOE的度数.
【详解】(1)解:∵EO⊥CD,
∴∠EOD=90°,
∵∠AOC=36°,
∴∠BOD=∠AOC=36°,
∴∠BOE=∠EOD-∠BOD=54°;
(2)解:∵∠BOD:∠BOC=1:5,
∴∠BOC=5∠BOD,
∵∠BOC+∠BOD=180°,
∴6∠BOD=180°,
∴∠BOD=30°,
∵EO⊥CD,
∴∠EOD=90°,
∴∠BOE=∠EOD-∠BOD=60°,
∴∠AOE=180°-∠BOE=120°.
【点睛】本题主要考查了几何中角度的计算,垂线的定义,对顶角,熟知相关知识是解题的关键.
23.(浙江省丽水市莲都区2021-2022学年七年级上学期期末数学试题)如图,直线AE与CD相交于点B,BF⊥AE.
(1)若∠DBE=60°,求∠FBD的度数;
(2)猜想∠CBE与∠DBF的数量关系,并说明理由.
【答案】(1)30°.
(2)∠CBE= 90°+∠DBF,理由见解析
【分析】(1)由垂线的定义可得∠DBF+∠DBE=90°,结合已知条件即可求解.
(2)根据∠CBE=∠ABD,∠ABD=∠ABF+∠DBF,可得∠CBE=∠ABF+∠DBF. 由BF⊥AE,得出∠ABF=90°, 即∠CBE= 90°+∠DBF.
【详解】(1)解:∵BF⊥AE,
∴∠DBF+∠DBE=90°,
∵∠DBE=60°,
∴∠DBF=90°-∠DBE=30°.
(2)∠CBE=∠DBF +90°.理由如下:
∵∠CBE=∠ABD,∠ABD=∠ABF+∠DBF,
∴∠CBE=∠ABF+∠DBF.
∵BF⊥AE,
∴∠ABF=90°,
∴∠CBE= 90°+∠DBF.
【点睛】本题考查了垂线的定义,几何图形中角度的计算,数形结合是解题的关键.
24.(广西壮族自治区百色市靖西市2021-2022学年七年级下学期期末数学试题)如图,直线AB、CD相交于点O,∠AOC=60°,射线OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
(1)求∠BOE的度数.
(2)过点O作射线OF⊥OE,求∠DOF的度数.
【答案】(1)24°
(2)54°或126°
【分析】(1)设∠BOE=2x,则∠EOD=3x;有对顶角相等可得∠BOD=∠AOC=60°,再由∠BOD=∠BOE+∠DOE列关于x的方程求得x,进而求得∠BOE;
(2)如图1、图2分两种情况,分别根据余角和角的和差计算即可.
【详解】(1)解:(1)设∠BOE=2x,则∠EOD=3x,
∵∠AOC=60°,
∴∠BOD=∠AOC=60°,
∵∠BOD=∠BOE+∠DOE,
∴2x+3x=60°,
∴x=12°,
∴∠BOE=2×12°=24°.
(2)解:如图1,
∵OF⊥OE,
∴∠FOE=90°,
∵∠DOE=60°-24°=36°,
∴∠DOF=∠FOE﹣∠DOE=90°﹣36°=54°;
如图2,
∵OF⊥OE,
∴∠FOE=90°,
∴∠DOF=∠FOE+∠EOD=90°+36°=126°.
∴∠DOF的度数是54°或126°.
【点睛】本题主要考查了对顶角相等、角的和差、垂直、余角等知识点,灵活运用相关知识和方程思想成为解答本题的关键.
25.(2023秋·河北石家庄·七年级石家庄市第九中学校考期末)已知:O 是直线上的一点,是直角,平分钝角.
(1)如图 1,若,求的度数;
(2)如图 2,平分,求的度数;
(3)当时,绕点 O 以每秒 5°沿逆时针方向旋转 t 秒(),请直接写出和之间的数量关系.
【答案】(1)
(2)
(3)时,;时,
【分析】(1)由补角及直角的定义可求得的度数,结合角平分线的定义可求解的度数;
(2)由角平分线的定义可得,进而可求解;
(3)可分两总情况:①时,时,分别计算可求解.
【详解】(1)解:∵,
∴,
∵是直角,
∴,
∴,
∵平分,
∴,
∴;
(2)解:∵平分平分,
∴,
∴,
∵,
∴;
(3)解:①时,由题意得,
∴,
∵平分,
∴,
∴,
∴;
②时,
由题意得,
∴,
∵平分,
∴,
∴,
∴.
综上,时,;时,.
【点睛】本题主要考查了几何中角度的计算,角平分线的定义,熟知角平分线的定义是解题的关键-.
26.(2023秋·河北石家庄·七年级石家庄市第四十一中学校考期末)如图,将两块直角三角板的直角顶点C叠放在一起.
(1) ______(填“”“”或“”);
(2)当时,求的度数;
(3)猜想与的数量关系,并说明理由;
(4)将三角板绕点C逆时针旋转一周,请直接写出此时为多少度时,与的大小是二倍关系.
【答案】(1);
(2);
(3),理由见解析;
(4).
【分析】(1)根据题意可知,,即可求出与的大小关系;
(2)根据角的数量关系进行和差计算即可得到答案;
(3)根据角的数量关系进行和差计算即可得到答案;
(4)分两种情况讨论:①当时;②当时,作出图形,结合(3)的结论,即可得到答案.
【详解】(1)解:两块直角三角板的直角顶点C叠放在一起,
,
,
,
故答案为:;
(2)解:,
,
;
(3)解:,
理由:,
,
,
;
(4)解:由(3)可知,,
①当时,如图1,
则,
,
;
②当时,如图2,
则
,
即当时,与的大小是二倍关系.
【点睛】本题考查了互余,旋转的性质,角的相关计算等知识,利用数形结合与分类讨论的思想,找出相关角的数量关系是解题关键.
27.(2023秋·安徽·七年级统考期末)如图,点是直线上的一点,,平分.
(1)如图1,若,则______°,______°.
(2)如图2,射线和分别位于直线的两侧,若,求的度数;
(3)如图3,射线和位于直线的下侧,求的度数.
【答案】(1),
(2)
(3)
【分析】(1)根据已知可得,再利用角平分线的定义求出,进行计算即可解答;
(2)利用平角是 先求出,然后利用角平分线的定义进行计算即可解答;
(3)根据进行计算即可解答;.
【详解】(1)解:∵,,
∴ ,
∵平分,
∴,
;
故答案为:,
(2)解:∵,
∴,
∵,
∴
∵平分,
∴,
∴;
(3)解:∵射线和位于直线的下侧
∴
∵是直线,
∴
【点睛】本题考查了角平分线及角的和差计算,掌握角平分线定义得出所求角与已知角的关系转化是关键.
28.(江西省抚州市实验学校2021-2022学年七年级下学期数学第一阶段综合练习题)如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且.请回答下列问题:
(1)∠AOE度数是 ;∠DOE度数是 ;
(2)将射线OE绕点O逆时针旋转α°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,OB是否平分∠DOF?请说明其理由;
②当OA⊥OF时,请求出α的度数.
【答案】(1)75°;135°
(2)①平分,理由见解析;②60°或者240°
【分析】(1)对于求解∠AOE与∠DOE的度数,首先从∠BOD=75°分析,它们之间有什么关系.根据对顶角相等,以及给出的角关系比例即可求出2个角的度数;
(2)要想得出OB是否平分∠DOF的结论,需要求出∠BOD与∠BOF的度数,进行比较即可得出结论;
②考虑到有两种情况即可,即为OF在如图所示位置与OF在上方位置.
【详解】(1)∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=75°
∵∠AOE=∠COE,
∴∠AOC=∠AOE+∠COE=∠COE=75°,
∴∠COE=45°,
∴∠AOE=30°,
∵∠AOD=180°﹣∠BOD=105°,
∠DOE=∠AOE+∠AOD=30°+105°=135°,
故答案为:75°,135°;
(2)①当OF平分∠BOE时
∵∠BOF=∠BOE=(∠COE+∠BOC)=×150°=75°,
∴∠BOF=∠BOD=75°,
∴当OF平分∠BOE时,OB是平分∠DOF.
②当OA⊥OF时,且OF在下方时,
∵∠COF=90°﹣∠AOC=90°﹣75°=15°,
∴α=∠COE+∠COF=45°+15°=60°,
当OA⊥OF时,且OF在上方时,OF相当于比在下方时多旋转了180°,
∴α=60°+180°=240°.
综上所述:当OA⊥OF时,α的度数为60°或者240°.
【点睛】本题考查了几何图形中角的计算,角平分线的定义,数形结合是解题的关键.
29.(辽宁省沈阳市沈河区第七中学2022-2023学年七年级上学期期中数学试题)【实践操作】三角尺中的数学.
(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,.
①若,则______;若,则_____;
②猜想:请直接写出与的数量关系:_______.
(2)如图乙若是两个同样的直角三角尺60°锐角的顶点虫重合在一起,,则请直接写出与的数量关系______;
(3)已知,(、都是锐角),如图3,若把它们的顶点O重合在一起,请直接写出与的数量关系: _______.
【答案】(1)①,;②
(2)
(3)
【分析】(1)①本题已知两块直角三角尺实际就是已知三角板的各个角的度数,根据角的和差就可以求出的度数;②根据前两个小问题的结论猜想与的大小关系,结合前两问的解决思路得出证明;
(2)根据(1)解决思路确定与的大小并证明;
(3)由于(都是锐角),而,进而得出结论.
【详解】(1)①∵
∴
∵
∴
∵
∴
∵
∴
故答案为:;
②猜想得(或与互补),
理由:∵
∴
∴;
故答案为:
(2),
理由如下:由于,
故 ;
故答案为:
(3),
理由:∵
∴ ,
即,
∴.
故答案为:
【点睛】本题考查余角与补角,掌握互为余角、互为补角的意义以及图形中角的和差关系是正确解答的关键.
30.(云南省红河哈尼族彝族自治州建水县2021-2022学年七年级上学期期末数学试题)如图1,点为直线上一点,过点作射线,使.将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点处逆时针旋转至图2,使一边在的内部.且恰好平分,求的度数;
(2)在图3中,延长线段得到射线,判断是否平分,请说明理由.
(3)将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角,则的值为______.(直接写出答案)
【答案】(1)
(2)平分;理由见解析
(3)30或12秒
【分析】(1)由角的平分线的定义和等角的余角相等求解;
(2)先由对顶角性质得=30°,再由,得,从而得出结论;
(3)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解.
【详解】(1)解:∵,
∴,
∵恰好平分,
∴,
∴,
∴;
(2)解:∵(对顶角),.
∴,
又∵,
∴.
∴
∴平分
(3)解:30或12.
设三角板绕点旋转的时间是秒,
∵,
∴,
如图,当的反向延长线平分时,
,
∴,
∴旋转的角度是,
∴,
∴;
如图,当平分时,
,
∴旋转的角度是,
∴,
∴,
综上,或,
即此时三角板绕点旋转的时间是30或12秒.
【点睛】此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、解答题
1.(黑龙江省哈尔滨市南岗区第六十九中学2022-2023学年度七年级上学期期中学业水平检测数学(五四制)试卷)如图,直线、相交于点,平分,,,求的度数.
2.(广东省东莞市石龙第二中学2021-2022学年七年级下学期期中数学试卷)如图,直线,相交于,是的角平分线.
(1)的对顶角是 ___________;
(2)若,求、的度数.
3.(黑龙江省哈尔滨德强学校2022—2023学年七年级上学期11月份线上教学问题诊断数学试题)如图,直线、相交于点,平分,垂足为点,且.
(1)如图,求的度数.
(2)在不添加任何辅助线的情况下,请直接写出图中与互余的角.
4.(2023秋·陕西延安·七年级统考期末)如图,点 A 、O 、B 在同一直线上,平分,若.
(1)求的度数;
(2)若平分,求的度数.
5.(2023春·广东阳江·七年级校考期中)如图,直线,相交于点,射线平分,若,求的度数.
6.(2023秋·江苏·七年级专题练习)如图,直线相交于点,于点.
(1)若,求的度数;
(2)若,请判断与垂直吗?如果垂直,请说明理由.
7.(2023秋·浙江·七年级专题练习)如图,.
(1)已知过直线上点有,条射线,,求的度数;
(2)若直线与直线相交于点,求图中各锐角的度数.
8.(2023秋·江苏无锡·七年级校考阶段练习)如图,直线相交于O,比大15°,是的2倍
(1)求的度数;
(2)试说明平分.
9.(四川省南充市高坪中学2020-2021学年七年级下学期期中考试数学试题)如图,直线和相交于点,,,,求的度数.
10.(西藏林芝市广东实验中学2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD.若∠AOC=70°,∠DOF=90°,求∠EOF的度数.
11.(重庆市江津区江津第五中学校2021-2022学年七年级下学期期中数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
12.(辽宁省大连市高新园区名校联盟2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分,,且.求和的度数.
13.(四川省成都市锦江区盐道街中学外语学校2021-2022学年七年级下学期期中数学试题)如图,直线,相交于点,平分.
(1)若,,求的度数;
(2)若平分,,求的度数.
14.(广东省广州市白云区六校2021-2022学年下学期七年级期中数学试卷-)如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.
(1)求∠AOF的度数.
(2)判断OE与OF的位置关系并说明理由.
15.(广东省惠州市大亚湾第三中学2021--2022学年七年级下学期数学期中考试试卷)如图,直线,相交于点,,垂足为.若,求的度数.
16.(福建省长汀县第四中学2021-2022学年七年级下学期第一次适应性练习数学试题)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
17.(广东省东莞市松山湖实验中学2020-2021学年七年级下学期期中数学试卷)如图,直线与相交于点,于点,平分,且,求的度数.
18.(河南省信阳市浉河区信阳文华寄宿学校2021-2022学年七年级下学期期末数学试题)如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
19.(湖北省省直辖县级行政单位天门市华斯达学校2021-2022学年七年级下学期3月月考数学试题)如图,已知直线AB、CD相交于点O,OE⊥AB,点O为垂足,OF平分∠AOC.
(1)若∠COE=54°,求∠DOF的度数;
(2)若∠COE∶∠EOF=2∶1,求∠DOF的度数.
20.(内蒙古自治区兴安盟扎赉特旗扎音德尔第三中学2021-2022学年七年级下学期期末数学试题)如图,两直线、相交于点,平分,如果::.
(1)求;
(2)若,,求.
21.(福建省建宁县城关中学片区2021-2022学年七年级下学期第一次单元检测(月考)数学试题)如图,直线相交于点O,平分,求:
(1)的度数;
(2)写出图中互余的角;
(3)的度数.
22.(河北省保定市满城区龙门中学2021-2022学年七年级下学期期末教学质量监测数学试题)如图,直线,相交于点,于点.
(1)若,求的度数;
(2)若,求的度数.
23.(浙江省丽水市莲都区2021-2022学年七年级上学期期末数学试题)如图,直线AE与CD相交于点B,BF⊥AE.
(1)若∠DBE=60°,求∠FBD的度数;
(2)猜想∠CBE与∠DBF的数量关系,并说明理由.
24.(广西壮族自治区百色市靖西市2021-2022学年七年级下学期期末数学试题)如图,直线AB、CD相交于点O,∠AOC=60°,射线OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
(1)求∠BOE的度数.
(2)过点O作射线OF⊥OE,求∠DOF的度数.
25.(2023秋·河北石家庄·七年级石家庄市第九中学校考期末)已知:O 是直线上的一点,是直角,平分钝角.
(1)如图 1,若,求的度数;
(2)如图 2,平分,求的度数;
(3)当时,绕点 O 以每秒 5°沿逆时针方向旋转 t 秒(),请直接写出和之间的数量关系.
26.(2023秋·河北石家庄·七年级石家庄市第四十一中学校考期末)如图,将两块直角三角板的直角顶点C叠放在一起.
(1) ______(填“”“”或“”);
(2)当时,求的度数;
(3)猜想与的数量关系,并说明理由;
(4)将三角板绕点C逆时针旋转一周,请直接写出此时为多少度时,与的大小是二倍关系.
27.(2023秋·安徽·七年级统考期末)如图,点是直线上的一点,,平分.
(1)如图1,若,则______°,______°.
(2)如图2,射线和分别位于直线的两侧,若,求的度数;
(3)如图3,射线和位于直线的下侧,求的度数.
28.(江西省抚州市实验学校2021-2022学年七年级下学期数学第一阶段综合练习题)如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且.请回答下列问题:
(1)∠AOE度数是 ;∠DOE度数是 ;
(2)将射线OE绕点O逆时针旋转α°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,OB是否平分∠DOF?请说明其理由;
②当OA⊥OF时,请求出α的度数.
29.(辽宁省沈阳市沈河区第七中学2022-2023学年七年级上学期期中数学试题)【实践操作】三角尺中的数学.
(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,.
①若,则______;若,则_____;
②猜想:请直接写出与的数量关系:_______.
(2)如图乙若是两个同样的直角三角尺60°锐角的顶点虫重合在一起,,则请直接写出与的数量关系______;
(3)已知,(、都是锐角),如图3,若把它们的顶点O重合在一起,请直接写出与的数量关系: _______.
30.(云南省红河哈尼族彝族自治州建水县2021-2022学年七年级上学期期末数学试题)如图1,点为直线上一点,过点作射线,使.将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点处逆时针旋转至图2,使一边在的内部.且恰好平分,求的度数;
(2)在图3中,延长线段得到射线,判断是否平分,请说明理由.
(3)将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角,则的值为______.(直接写出答案)
专题2.4相交线大题专练(重难点培优30题)
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷试题解答30道,共分成三个层组:基础过关题(第1-10题)、能力提升题(第11-20题)、培优压轴题(第21-30题),每个题组各10题,可以灵活选用.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、解答题
1.(黑龙江省哈尔滨市南岗区第六十九中学2022-2023学年度七年级上学期期中学业水平检测数学(五四制)试卷)如图,直线、相交于点,平分,,,求的度数.
【答案】
【分析】依据,,可得,再根据平分,即可得出,依据平角定义得到.
【详解】解:∵,
∴.
∵.
∴.
∵平分.
∴.
∴.
∵
∴.
【点睛】本题主要考查了垂线的意义,角平分线的定义以及余角的综合运用,正确的识别图形是解题的关键.
2.(广东省东莞市石龙第二中学2021-2022学年七年级下学期期中数学试卷)如图,直线,相交于,是的角平分线.
(1)的对顶角是 ___________;
(2)若,求、的度数.
【答案】(1)
(2),
【分析】(1)根据对顶角定义直接解答即可;
(2)由邻补角定义求出的度数,再根据角平分线定义求出,即可得到的度数.
【详解】(1)解:由对顶角的定义可知,的对顶角是,
故答案为:;
(2),,
,
又是的角平分线.
,
,
答:的度数为.
【点睛】此题考查了几何图形中角度的计算,角平分线的定义,邻补角定义,对顶角定义,正确理解各定义并理解图形中各角的位置关系及数量关系是解题的关键.
3.(黑龙江省哈尔滨德强学校2022—2023学年七年级上学期11月份线上教学问题诊断数学试题)如图,直线、相交于点,平分,垂足为点,且.
(1)如图,求的度数.
(2)在不添加任何辅助线的情况下,请直接写出图中与互余的角.
【答案】(1)
(2)
【分析】(1)先根据垂直的定义得到,再根据平角的定义得到,再根据角平分线的定义得到则,据此求出,即可利用平角的定义求出;
(2)根据余角的定义进行推理即可.
【详解】(1)解:∵,
∴,
∴,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴;
(2)解:∵,
∴,
∴,
∵,
∴,
∵∵平分,
∴,
∴,
∴的余角有.
【点睛】本题主要考查了垂直的定义,角平分线的定义,余角的定义,平角的定义,熟知相关知识是解题的关键.
4.(2023秋·陕西延安·七年级统考期末)如图,点 A 、O 、B 在同一直线上,平分,若.
(1)求的度数;
(2)若平分,求的度数.
【答案】(1)
(2)
【分析】(1)根据平角的定义、角平分线的定义求出,结合图形计算得到答案;
(2)根据角平分线的定义求出∠DOE,结合图形计算得到答案.
【详解】(1)解:∵点A、O、B在同一直线上,平分,
∴,
∴;
(2)解:∵平分,
∴,
∴.
【点睛】本题考查的是角的计算、角平分线的定义,从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.
5.(2023春·广东阳江·七年级校考期中)如图,直线,相交于点,射线平分,若,求的度数.
【答案】
【分析】首先根据角平分线的定义可求得的度数,由垂线的定义可知,故此可求得的度数.
【详解】∵平分,
∴,
∵,
∴,
∴.
【点睛】本题考查了角平分线的定义和垂线的定义,掌握此定义是解题的关键.
6.(2023秋·江苏·七年级专题练习)如图,直线相交于点,于点.
(1)若,求的度数;
(2)若,请判断与垂直吗?如果垂直,请说明理由.
【答案】(1)
(2)垂直,理由见解析
【分析】(1)根据和平角的定义计算即可;
(2)利用等量代换,可计算出,即可证明出与垂直.
【详解】(1)解:,
,
,
,
直线相交于点,
,
故的度数为:;
(2)解:垂直,
理由如下:
,
,
,
,
,
故与垂直.
【点睛】本题考查了垂直、对顶角、等量代换等知识点,解题的关键是理解垂直、对顶角的定义.
7.(2023秋·浙江·七年级专题练习)如图,.
(1)已知过直线上点有,条射线,,求的度数;
(2)若直线与直线相交于点,求图中各锐角的度数.
【答案】(1)
(2)图中各锐角的度数为
【分析】(1)根据得出,根据图形可得,,,即可求解;
(2)根据,得出,进而即可求解.
【详解】(1)解:∵,
∴,
∵,
∴,
∴,.
∴;
(2)解:∵,
∴,
∴,
∴,
∴,
∴.
∴图中各锐角的度数为.
【点睛】本题考查了垂线、对顶角、邻补角,解决本题的关键是掌握垂线、对顶角、邻补角定义.
8.(2023秋·江苏无锡·七年级校考阶段练习)如图,直线相交于O,比大15°,是的2倍
(1)求的度数;
(2)试说明平分.
【答案】(1)50°
(2)见解析
【分析】(1)设的度数为x,则,根据平角的定义可得,解方程即可得到答案;
(2)根据(1)所求得到,根据平角的定义求出则,由此即可证明结论.
【详解】(1)解:设的度数为x,
由题意得:,
∵直线相交于O,
∴,
∴,
∴,
∴;
(2)证明:由(1)得:,
∴,
∴,即平分.
【点睛】本题主要考查了几何中角度的计算,一元一次方程的应用,正确理清角之间的关系是解题的关键.
9.(四川省南充市高坪中学2020-2021学年七年级下学期期中考试数学试题)如图,直线和相交于点,,,,求的度数.
【答案】
【分析】根据,得出,根据,可得,根据角的倍分关系,可得∠的度数,根据是邻补角,可得答案.
【详解】解:∵,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴.
∴.
【点睛】本题考查垂直的性质、角的和差、角的倍分关系、邻补角的性质等知识,是基础考点,掌握相关知识是解题关键.
10.(西藏林芝市广东实验中学2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD.若∠AOC=70°,∠DOF=90°,求∠EOF的度数.
【答案】55°
【分析】根据对顶角和角平分线的定义求出∠BOE的度数,再根据已知求出∠BOF的度数,即可求出∠EOF的度数.
【详解】解:∵∠AOC=70°,
∴∠BOD=∠AOC=70°,
∵OE平分∠BOD,
∴∠BOE=∠DOE=∠BOD=35°,
又∵∠DOF=90°,
∴
∴.
【点睛】本题考查角平分线、对顶角,角的和差运算,掌握角平分线的定义,理解对顶角相等是正确解答的关键.
11.(重庆市江津区江津第五中学校2021-2022学年七年级下学期期中数学试题)如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC=76°,求∠BOF的度数;
(2)若∠BOF=36°,求∠AOC的度数;
【答案】(1)∠BOF=33°
(2)∠AOC=72°
【分析】(1)先根据对顶角相等求出∠BOD=76°,再由角平分线定义得∠DOE=∠BOE=38°,由邻补角得∠COE=142°,再根据角平分线定义得∠EOF=71°,从而可得结论.
(2)利用角平分的定义得出,进而表示出各角求出答案.
【详解】(1)∵∠AOC、∠BOD是对顶角,
∴∠BOD=∠AOC=76°,
∵OE平分∠BOD,
∴∠DOE=∠BOE=∠BOD=38°
∴∠COE=142°,
∵OF平分∠COE.
∴∠EOF=∠COE=71°,
又∠BOE+∠BOF=∠EOF,
∴∠BOF=∠EOF ∠BOE=71° 38°=33°,
(2)∵OE平分∠BOD,OF平分∠COE,
∴,
∴设,则,
故,,
则,
解得,
故∠AOC=72°.
【点睛】本题考查了角平分线的定义和对顶角的性质,解决本题的关键是掌握对顶角的定义(从一个角的顶点引出一条射线,把这个角分成两个完全相同的角,这条射线叫做这个角的角平分线).
12.(辽宁省大连市高新园区名校联盟2021-2022学年七年级下学期期中考试数学试题)如图,直线AB、CD相交于点O,OE平分,,且.求和的度数.
【答案】,
【分析】根据题意和角平分线的性质得,根据对顶角相等可得,根据得,可得,即可得.
【详解】解:∵OE平分,,
∴,
又∵,
∴,
∵,
∴,
∴,
∴.
【点睛】本题考查了角平分线,对顶角,邻补角,解题的关键是掌握角平分线的性质,对顶角相等并认真计算.
13.(四川省成都市锦江区盐道街中学外语学校2021-2022学年七年级下学期期中数学试题)如图,直线,相交于点,平分.
(1)若,,求的度数;
(2)若平分,,求的度数.
【答案】(1)70°
(2)50°
【分析】(1)根据角平分线的性质可得,根据垂线的定义以及已知条件求得,继而求得,根据对顶角相等即可求解;
(2)根据角平分线的性质可得,,设,则,根据平角的定义建立方程,解方程即可求解.
【详解】(1)解:平分,
,
,,
,
,
∴
;
(2)平分,
,
,
设,则,
,
解得:,
故的度数为:.
【点睛】本题考查了几何图形中角度的计算,角平分线的定义,垂线的定义,一元一次方程的应用,数形结合是解题的关键.
14.(广东省广州市白云区六校2021-2022学年下学期七年级期中数学试卷-)如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠BOC,∠2:∠1=4:1.
(1)求∠AOF的度数.
(2)判断OE与OF的位置关系并说明理由.
【答案】(1)108°
(2),理由见解析
【分析】(1)设∠1=x°,则∠2=4x°,求出,,根据∠BOC+∠BOD=180°,求出x=18,代入∠AOF=∠AOC+∠COF求出即可.
(2)根据(1)的结论得出,即可求解.
(1)
解:设∠1=x°,则∠2=4x°,
∵OE平分∠BOD,OF平分∠BOC,
∴,
∵∠BOC+∠BOD=180°,
∴8x+2x=180,
∴x=18,
∴∠AOC=∠DOB=2x=36°,∠1=18°,∠2=72°,
∴∠AOF=∠AOC+∠2=36°+72°=108°.
(2)
由(1)可得∠1=18°,∠2=72°,
∴,
∴.
【点睛】本题考查了几何图形中角度的计算,角平分线的定义,数形结合是解题的关键.
15.(广东省惠州市大亚湾第三中学2021--2022学年七年级下学期数学期中考试试卷)如图,直线,相交于点,,垂足为.若,求的度数.
【答案】150°
【分析】由EO⊥AB可得∠BOE=90°,由,,可得∠AOC,从而可得∠BOD,这样由∠DOE=∠BOE+∠BOD即可求得∠DOE的度数.
【详解】解:,,
,
,
,
答:的度数为.
【点睛】本题考查了垂线、对顶角、邻补角,求出∠AOC的度数是解题的关键.
16.(福建省长汀县第四中学2021-2022学年七年级下学期第一次适应性练习数学试题)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
【答案】(1)OF⊥OD,理由见解析;
(2)∠EOF=60°
【分析】(1)利用角平分线的定义结合已知求出∠FOD=90°即可得出答案;
(2)求出∠AOC的度数,再利用对顶角的性质和角平分线的定义求出∠BOD=∠AOC=∠EOD=30°,进而得出∠EOF的度数.
(1)
解:OF⊥OD,
理由:∵OF平分∠AOE,
∴∠AOF=∠FOE,
∵∠DOE=∠BOD,
∴∠AOF+∠BOD=∠FOE+∠DOE=×180°=90°,即∠FOD=90°,
∴OF与OD的位置关系是OF⊥OD;
(2)
∵∠AOC:∠AOD=1:5,
∴∠AOC=×180°=30°,
∴∠BOD=∠AOC=∠EOD=30°,
∴∠AOE=120°,
∴∠EOF=∠AOE=60°.
【点睛】此题主要考查了角平分线的定义以及邻补角的性质,正确得出各角之间的关系是解题关键.
17.(广东省东莞市松山湖实验中学2020-2021学年七年级下学期期中数学试卷)如图,直线与相交于点,于点,平分,且,求的度数.
【答案】70°
【分析】根据垂直的定义,求得,根据,以及对顶角相等可得,然后根据角平分线的定义即可求解.
【详解】,,
,
,
,
又平分,
.
【点睛】本题考查了垂线的定义,几何图形中角度的计算,对顶角相等,角平分线的定义,数形结合求得是解题的关键.
18.(河南省信阳市浉河区信阳文华寄宿学校2021-2022学年七年级下学期期末数学试题)如图,已知点O在直线AB上,射线OE平分∠AOC,过点O作OD⊥OE,G是射线OB上一点,连接DG,使∠ODG+∠DOG=90°.
(1)求证:∠AOE=∠ODG;
(2)若∠ODG=∠C,试判断CD与OE的位置关系,并说明理由.
【答案】(1)证明见解析
(2)CDOE,理由见解析
【分析】(1)由OD⊥OE得到∠EOC+∠COD=∠AOE+∠DOG=90°,再利用等角的余角相等即可证明∠AOE=∠ODG;
(2)证明∠EOC=∠C,利用内错角相等两直线平行,即可证明CDOE.
【详解】(1)证明:∵OD⊥OE,
∴∠EOC+∠COD=∠AOE+∠DOG=90°,
∵∠ODG+∠DOG=90°,
∴∠AOE=∠ODG;
(2)解:CDOE.理由如下:
由(1)得∠AOE=∠ODG,
∵射线OE平分∠AOC,
∴∠AOE=∠EOC,
∵∠ODG=∠C,
∴∠EOC=∠C,
∴CDOE.
【点睛】本题考查了角平分线定义,垂直的定义,平行线的判定,等角的余角相等,正确识图是解题的关键.
19.(湖北省省直辖县级行政单位天门市华斯达学校2021-2022学年七年级下学期3月月考数学试题)如图,已知直线AB、CD相交于点O,OE⊥AB,点O为垂足,OF平分∠AOC.
(1)若∠COE=54°,求∠DOF的度数;
(2)若∠COE∶∠EOF=2∶1,求∠DOF的度数.
【答案】(1)∠DOF=108°;
(2)∠DOF=112.5°.
【分析】(1)先由OE⊥AB得出∠AOE=∠BOE=90°,再根据角平分线定义求出∠COF=72°,然后由∠DOF=180°-∠COF即可求解;
(2)设∠EOF=x°,则∠COE=2x°,则∠COF=3x°,再根据角平分线定义求出∠AOF=∠COF=3x°,所以∠AOE=4x°,由垂直的定义可知∠AOE=90°,则4x=90,解之,求出x即可.
【详解】(1)解:∵OE⊥AB,
∴∠AOE=90°;
∵∠COE=54°,
∴∠AOC=∠AOE+∠COE=144°,
∵OF平分∠AOC,
∴∠COF=∠AOC=72°,
∴∠DOF=180°-∠COF=108°;
(2)解:设∠EOF=x°,则∠COE=2x°,
∴∠COF=3x°,
∵OF平分∠AOC,
∴∠AOF=∠COF=3x°,
∴∠AOE=4x°,
∵OE⊥AB,
∴∠AOE=90°,
∴4x=90,解得x=22.5,
∴∠COF=3x°=67.5°,
∴∠DOF=180°-∠COF=112.5°.
【点睛】本题考查了角的计算,根据垂直的定义、角的和差关系列方程进行求解,即可计算出答案,难度适中.
20.(内蒙古自治区兴安盟扎赉特旗扎音德尔第三中学2021-2022学年七年级下学期期末数学试题)如图,两直线、相交于点,平分,如果::.
(1)求;
(2)若,,求.
【答案】(1)145°
(2)125°
【分析】(1)根据邻补角的性质和已知求出和的度数,根据对顶角相等求出和的度数,根据角平分线的定义求出的度数,可以得到的度数;
(2)根据垂直的定义得到,根据互余的性质求出的度数,计算得到答案.
【详解】(1)解:,::,
,,
,,
平分,
,
.
(2)解:,
,
平分,
,
,
.
【点睛】本题考查的是邻补角的性质、对顶角的性质和角平分线的定义,掌握邻补角互补、对顶角相等和垂直的定义是解题的关键.
21.(福建省建宁县城关中学片区2021-2022学年七年级下学期第一次单元检测(月考)数学试题)如图,直线相交于点O,平分,求:
(1)的度数;
(2)写出图中互余的角;
(3)的度数.
【答案】(1)70°
(2)∠BOF与∠BOD互余,∠EOF与∠EOD互余,∠EOF与∠BOE互余,∠BOF与∠AOC互余
(3)55°
【分析】(1)根据对顶角相等即可得到;
(2)根据余角的定义求解即可;
(3)先根据角平分线的定义求出∠DOE=35°,则∠EOF=∠DOF-∠DOE=55°.
【详解】(1)解:由题意得;
(2)解:∵∠COF=90°,
∴∠DOF=180°-∠COF=90°,
∴∠BOF+∠BOD=90°,∠EOF+∠EOD=90°,
∵OE平分∠BOD,
∴∠BOE=∠DOE,
∴∠EOF+∠BOE=90°,
∵∠AOC=∠BOD,
∴∠BOF+∠AOC=90°,
∴∠BOF与∠BOD互余,∠EOF与∠EOD互余,∠EOF与∠BOE互余,∠BOF与∠AOC互余;
(3)解:∵∠BOD=70°,OE平分∠BOD,
∴∠DOE=35°,
∴∠EOF=∠DOF-∠DOE=55°.
【点睛】本题主要考查了几何中角度的计算,角平分线的定义,对顶角相等,余角的定义,熟知相关知识是解题的关键.
22.(河北省保定市满城区龙门中学2021-2022学年七年级下学期期末教学质量监测数学试题)如图,直线,相交于点,于点.
(1)若,求的度数;
(2)若,求的度数.
【答案】(1)54°
(2)120°
【分析】(1)先由垂直的定义得到∠EOD=90°,再由对顶角相等得到∠BOD=∠AOC=36°,由此求解即可;
(2)根据平角的定义结合已知条件求出∠BOD的度数,进而求出∠BOE的度数,最后根据平角的定义即可求出∠AOE的度数.
【详解】(1)解:∵EO⊥CD,
∴∠EOD=90°,
∵∠AOC=36°,
∴∠BOD=∠AOC=36°,
∴∠BOE=∠EOD-∠BOD=54°;
(2)解:∵∠BOD:∠BOC=1:5,
∴∠BOC=5∠BOD,
∵∠BOC+∠BOD=180°,
∴6∠BOD=180°,
∴∠BOD=30°,
∵EO⊥CD,
∴∠EOD=90°,
∴∠BOE=∠EOD-∠BOD=60°,
∴∠AOE=180°-∠BOE=120°.
【点睛】本题主要考查了几何中角度的计算,垂线的定义,对顶角,熟知相关知识是解题的关键.
23.(浙江省丽水市莲都区2021-2022学年七年级上学期期末数学试题)如图,直线AE与CD相交于点B,BF⊥AE.
(1)若∠DBE=60°,求∠FBD的度数;
(2)猜想∠CBE与∠DBF的数量关系,并说明理由.
【答案】(1)30°.
(2)∠CBE= 90°+∠DBF,理由见解析
【分析】(1)由垂线的定义可得∠DBF+∠DBE=90°,结合已知条件即可求解.
(2)根据∠CBE=∠ABD,∠ABD=∠ABF+∠DBF,可得∠CBE=∠ABF+∠DBF. 由BF⊥AE,得出∠ABF=90°, 即∠CBE= 90°+∠DBF.
【详解】(1)解:∵BF⊥AE,
∴∠DBF+∠DBE=90°,
∵∠DBE=60°,
∴∠DBF=90°-∠DBE=30°.
(2)∠CBE=∠DBF +90°.理由如下:
∵∠CBE=∠ABD,∠ABD=∠ABF+∠DBF,
∴∠CBE=∠ABF+∠DBF.
∵BF⊥AE,
∴∠ABF=90°,
∴∠CBE= 90°+∠DBF.
【点睛】本题考查了垂线的定义,几何图形中角度的计算,数形结合是解题的关键.
24.(广西壮族自治区百色市靖西市2021-2022学年七年级下学期期末数学试题)如图,直线AB、CD相交于点O,∠AOC=60°,射线OE把∠BOD分成两个角,且∠BOE:∠EOD=2:3.
(1)求∠BOE的度数.
(2)过点O作射线OF⊥OE,求∠DOF的度数.
【答案】(1)24°
(2)54°或126°
【分析】(1)设∠BOE=2x,则∠EOD=3x;有对顶角相等可得∠BOD=∠AOC=60°,再由∠BOD=∠BOE+∠DOE列关于x的方程求得x,进而求得∠BOE;
(2)如图1、图2分两种情况,分别根据余角和角的和差计算即可.
【详解】(1)解:(1)设∠BOE=2x,则∠EOD=3x,
∵∠AOC=60°,
∴∠BOD=∠AOC=60°,
∵∠BOD=∠BOE+∠DOE,
∴2x+3x=60°,
∴x=12°,
∴∠BOE=2×12°=24°.
(2)解:如图1,
∵OF⊥OE,
∴∠FOE=90°,
∵∠DOE=60°-24°=36°,
∴∠DOF=∠FOE﹣∠DOE=90°﹣36°=54°;
如图2,
∵OF⊥OE,
∴∠FOE=90°,
∴∠DOF=∠FOE+∠EOD=90°+36°=126°.
∴∠DOF的度数是54°或126°.
【点睛】本题主要考查了对顶角相等、角的和差、垂直、余角等知识点,灵活运用相关知识和方程思想成为解答本题的关键.
25.(2023秋·河北石家庄·七年级石家庄市第九中学校考期末)已知:O 是直线上的一点,是直角,平分钝角.
(1)如图 1,若,求的度数;
(2)如图 2,平分,求的度数;
(3)当时,绕点 O 以每秒 5°沿逆时针方向旋转 t 秒(),请直接写出和之间的数量关系.
【答案】(1)
(2)
(3)时,;时,
【分析】(1)由补角及直角的定义可求得的度数,结合角平分线的定义可求解的度数;
(2)由角平分线的定义可得,进而可求解;
(3)可分两总情况:①时,时,分别计算可求解.
【详解】(1)解:∵,
∴,
∵是直角,
∴,
∴,
∵平分,
∴,
∴;
(2)解:∵平分平分,
∴,
∴,
∵,
∴;
(3)解:①时,由题意得,
∴,
∵平分,
∴,
∴,
∴;
②时,
由题意得,
∴,
∵平分,
∴,
∴,
∴.
综上,时,;时,.
【点睛】本题主要考查了几何中角度的计算,角平分线的定义,熟知角平分线的定义是解题的关键-.
26.(2023秋·河北石家庄·七年级石家庄市第四十一中学校考期末)如图,将两块直角三角板的直角顶点C叠放在一起.
(1) ______(填“”“”或“”);
(2)当时,求的度数;
(3)猜想与的数量关系,并说明理由;
(4)将三角板绕点C逆时针旋转一周,请直接写出此时为多少度时,与的大小是二倍关系.
【答案】(1);
(2);
(3),理由见解析;
(4).
【分析】(1)根据题意可知,,即可求出与的大小关系;
(2)根据角的数量关系进行和差计算即可得到答案;
(3)根据角的数量关系进行和差计算即可得到答案;
(4)分两种情况讨论:①当时;②当时,作出图形,结合(3)的结论,即可得到答案.
【详解】(1)解:两块直角三角板的直角顶点C叠放在一起,
,
,
,
故答案为:;
(2)解:,
,
;
(3)解:,
理由:,
,
,
;
(4)解:由(3)可知,,
①当时,如图1,
则,
,
;
②当时,如图2,
则
,
即当时,与的大小是二倍关系.
【点睛】本题考查了互余,旋转的性质,角的相关计算等知识,利用数形结合与分类讨论的思想,找出相关角的数量关系是解题关键.
27.(2023秋·安徽·七年级统考期末)如图,点是直线上的一点,,平分.
(1)如图1,若,则______°,______°.
(2)如图2,射线和分别位于直线的两侧,若,求的度数;
(3)如图3,射线和位于直线的下侧,求的度数.
【答案】(1),
(2)
(3)
【分析】(1)根据已知可得,再利用角平分线的定义求出,进行计算即可解答;
(2)利用平角是 先求出,然后利用角平分线的定义进行计算即可解答;
(3)根据进行计算即可解答;.
【详解】(1)解:∵,,
∴ ,
∵平分,
∴,
;
故答案为:,
(2)解:∵,
∴,
∵,
∴
∵平分,
∴,
∴;
(3)解:∵射线和位于直线的下侧
∴
∵是直线,
∴
【点睛】本题考查了角平分线及角的和差计算,掌握角平分线定义得出所求角与已知角的关系转化是关键.
28.(江西省抚州市实验学校2021-2022学年七年级下学期数学第一阶段综合练习题)如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且.请回答下列问题:
(1)∠AOE度数是 ;∠DOE度数是 ;
(2)将射线OE绕点O逆时针旋转α°(0°<α<360°)到OF.
①如图2,当OF平分∠BOE时,OB是否平分∠DOF?请说明其理由;
②当OA⊥OF时,请求出α的度数.
【答案】(1)75°;135°
(2)①平分,理由见解析;②60°或者240°
【分析】(1)对于求解∠AOE与∠DOE的度数,首先从∠BOD=75°分析,它们之间有什么关系.根据对顶角相等,以及给出的角关系比例即可求出2个角的度数;
(2)要想得出OB是否平分∠DOF的结论,需要求出∠BOD与∠BOF的度数,进行比较即可得出结论;
②考虑到有两种情况即可,即为OF在如图所示位置与OF在上方位置.
【详解】(1)∵直线AB、CD相交于点O,
∴∠BOD=∠AOC=75°
∵∠AOE=∠COE,
∴∠AOC=∠AOE+∠COE=∠COE=75°,
∴∠COE=45°,
∴∠AOE=30°,
∵∠AOD=180°﹣∠BOD=105°,
∠DOE=∠AOE+∠AOD=30°+105°=135°,
故答案为:75°,135°;
(2)①当OF平分∠BOE时
∵∠BOF=∠BOE=(∠COE+∠BOC)=×150°=75°,
∴∠BOF=∠BOD=75°,
∴当OF平分∠BOE时,OB是平分∠DOF.
②当OA⊥OF时,且OF在下方时,
∵∠COF=90°﹣∠AOC=90°﹣75°=15°,
∴α=∠COE+∠COF=45°+15°=60°,
当OA⊥OF时,且OF在上方时,OF相当于比在下方时多旋转了180°,
∴α=60°+180°=240°.
综上所述:当OA⊥OF时,α的度数为60°或者240°.
【点睛】本题考查了几何图形中角的计算,角平分线的定义,数形结合是解题的关键.
29.(辽宁省沈阳市沈河区第七中学2022-2023学年七年级上学期期中数学试题)【实践操作】三角尺中的数学.
(1)如图1,将两块直角三角尺的直角顶点C叠放在一起,.
①若,则______;若,则_____;
②猜想:请直接写出与的数量关系:_______.
(2)如图乙若是两个同样的直角三角尺60°锐角的顶点虫重合在一起,,则请直接写出与的数量关系______;
(3)已知,(、都是锐角),如图3,若把它们的顶点O重合在一起,请直接写出与的数量关系: _______.
【答案】(1)①,;②
(2)
(3)
【分析】(1)①本题已知两块直角三角尺实际就是已知三角板的各个角的度数,根据角的和差就可以求出的度数;②根据前两个小问题的结论猜想与的大小关系,结合前两问的解决思路得出证明;
(2)根据(1)解决思路确定与的大小并证明;
(3)由于(都是锐角),而,进而得出结论.
【详解】(1)①∵
∴
∵
∴
∵
∴
∵
∴
故答案为:;
②猜想得(或与互补),
理由:∵
∴
∴;
故答案为:
(2),
理由如下:由于,
故 ;
故答案为:
(3),
理由:∵
∴ ,
即,
∴.
故答案为:
【点睛】本题考查余角与补角,掌握互为余角、互为补角的意义以及图形中角的和差关系是正确解答的关键.
30.(云南省红河哈尼族彝族自治州建水县2021-2022学年七年级上学期期末数学试题)如图1,点为直线上一点,过点作射线,使.将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的下方.
(1)将图1中的三角板绕点处逆时针旋转至图2,使一边在的内部.且恰好平分,求的度数;
(2)在图3中,延长线段得到射线,判断是否平分,请说明理由.
(3)将图1中的三角板绕点按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,第秒时,直线恰好平分锐角,则的值为______.(直接写出答案)
【答案】(1)
(2)平分;理由见解析
(3)30或12秒
【分析】(1)由角的平分线的定义和等角的余角相等求解;
(2)先由对顶角性质得=30°,再由,得,从而得出结论;
(3)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解.
【详解】(1)解:∵,
∴,
∵恰好平分,
∴,
∴,
∴;
(2)解:∵(对顶角),.
∴,
又∵,
∴.
∴
∴平分
(3)解:30或12.
设三角板绕点旋转的时间是秒,
∵,
∴,
如图,当的反向延长线平分时,
,
∴,
∴旋转的角度是,
∴,
∴;
如图,当平分时,
,
∴旋转的角度是,
∴,
∴,
综上,或,
即此时三角板绕点旋转的时间是30或12秒.
【点睛】此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
