新人教版数学八年级上册第十三章轴对称13.3.1《等腰三角形》课时练习.docx
文档属性
| 名称 | 新人教版数学八年级上册第十三章轴对称13.3.1《等腰三角形》课时练习.docx |

|
|
| 格式 | docx | ||
| 文件大小 | 68.9KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-19 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新人教版数学八年级上册
第十三章轴对称13.3.1等腰三角形课时练习
一.选择题
1.知等腰三角形的一个底角为40°,则这个等腰三角形的顶角为( )
A.40° B.100° C.40°或100° D.50°或70°
答案:B
知识点:等腰三角形的性质;三角形内角和定理
解析:解答:∵等腰三角形的一个底角为40°∴顶角为180°-(40°+40°)=100°,故B项正确.
分析:结合所给条件根据等腰三角形性质可得两底角和为80°,再根据三角形内角和定理可得顶角的度数.
2.如图, AB=AC ,BD=BC, 若∠A=50°,则∠ABD=度数是( )
A.15° B.20° C.25° D. 30°
答案:A
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵AB=AC, ∠A=50°∴∠ABC=∠ACB=65°,∵BD=BC,∴∠BDC=∠ACB=65°则∠DBC=50°, ∠ABD=∠ABC -∠DBC =15°,故A项正确.
分析:根据所给条件利用等腰三角形性质在△ABC可得∠ABC=∠ACB=65°,在△BCD可得∠BDC=∠ACB=65°,再三角形内角和定理得∠DBC=50°,则∠ABD=∠ABC -∠DBC =15°
试3.等腰三角形的两条边长分别为3,6,那么它的周长为( )
A.15 B.12 C.12或15 D.不能确定
答案:A
知识点:等腰三角形的性质;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为3,6分情况讨论 :(1)边为3.3.6,由三角形三边关系可知不能组成三角形.(2)3.6.6可组成三角形,则周长为:6+6+3=15. 故A项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即3.6.6,则周长为15.
4.已知等腰三角形的两条边长分别是2和4,则它的周长是 ( )
A.8 B.10 C.8或10 D.无法确定
答案:B
知识点:;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为2和4分情况讨论 :(1)边为2.2.4,由三角形三边关系可知不能组成三角形.(2)2.4.4可组成三角形,则周长为:2+4+4=10. 故B项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即2.4.4,则周长为10.
5.已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A.10 B.13 C.17 D.13或17
答案:C
知识点:等腰三角形的性质;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为3和7分情况讨论 :(1)边为3.3.7,由三角形三边关系可知不能组成三角形.(2)3.7.7可组成三角形,则周长为:3+7+7=17. 故C项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即3.7.7,则周长为17.
6.等腰三角形的两边长是2和5,它的周长是( )
A.9 B.12 C.9或12 D.7
答案:B
知识点:等腰三角形的性质;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为2和5分情况讨论 :(1)边为2.2.5,由三角形三边关系可知不能组成三角形.(2)2.5.5可组成三角形,则周长为:2+5+5=12. 故B项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即2.5.5,则周长为12.
7.已知一个等腰三角形两内角的度数之比1:4,则这个等腰三角形顶角的度数为()
A.20°;B.120°;C.20°或120°;D.30°;
答案:C
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵等腰三角形的两内角的度数之比为1:4分情况讨论 :(1)顶角为x底角4X,则4X+4X+X =180°,X=20°;(2) 顶角为4X底角X,则4X+X+X =180°,x=30,°则顶角为120°, 故C项正确.
分析:根据等腰三角形性质可知顶角有两种情况,结合三角形三内角和可得顶角度数.
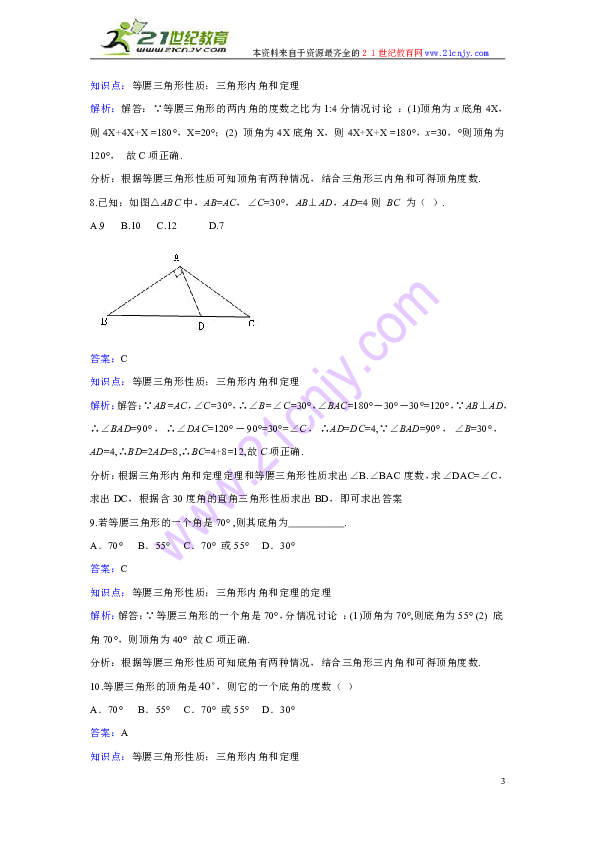
8.已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4则 BC 为( ).
A.9 B.10 C.12 D.7
答案:C
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵AB=AC,∠C=30°,∴∠B=∠C=30°,∠BAC=180°-30°-30°=120°,∵AB⊥AD,∴∠BAD=90°,∴∠DAC=120°-90°=30°=∠C,∴AD=DC=4,∵∠BAD=90°,∠B=30°,AD=4,∴BD=2AD=8,∴BC=4+8=12,故C项正确.
分析:根据三角形内角和定理定理和等腰三角形性质求出∠B.∠BAC度数,求∠DAC=∠C,求出DC,根据含30度角的直角三角形性质求出BD,即可求出答案
9.若等腰三角形的一个角是70° ,则其底角为 .
A.70° B.55° C.70° 或 55° D.30°
答案:C
知识点:等腰三角形性质;三角形内角和定理的定理
解析:解答:∵等腰三角形的一个角是70°,分情况讨论 :(1)顶角为70°,则底角为 55° (2) 底角70°,则顶角为40° 故C项正确.
分析:根据等腰三角形性质可知底角有两种情况,结合三角形三内角和可得顶角度数.
10.等腰三角形的顶角是,则它的一个底角的度数( )
A.70° B.55° C.70° 或 55° D.30°
答案:A
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵等腰三角形的顶角是,则底角70°故A项正确.
分析:根据等腰三角形性质可知两底角相等,结合三角形三内角和可得底角度数.
11.等腰三角形的底角是20°,则顶角的度数是( ). .
A.140° B.55° C.70° D.30°
答案:A
知识点:等腰三角形性质;三角形内角和定理
解析:解答:等腰三角形的底角是20°,顶角为140° 故A项正确.
分析:根据等腰三角形性质可知两底角相等,结合三角形三内角和可得顶角度数.
12.若等腰三角形中有一个角等于110°,则其它两个角的度数为( ).
A.70° B.110°和 70° C.35°和35° D.30°和70°
答案:C
知识点:等腰三角形性质;三角形内角和定理
解析:解答:等腰三角形的一个角是110°,其它两个角35°和35°,故C项正确.
分析:由等腰三角形性质可知有两个角相等,根据已知角的度数利用三角形三内角和可得其它两个角的度数.
13.若等腰三角形中有一个角等于50° ,则其它两个角的度数为()。
A.70° B.50°和 80 或 65°和65° C.65°和65° D.50°和 80°
答案:B
知识点:等腰三角形性质;三角形内角和定理
解析:解答:等腰三角形中有一个角等于50° ,分两种情况讨论:(1)50° 为底角,其它两个角的度数为50° 和 80°; (2)50° 为顶角,其它两个角的度数为65° 和65°. 故B项正确
分析:根据已知角的度数分两种情况讨论,利用三角形三内角和可得其它两个角的度数.
14.已知等腰三角形底边长为6Cm,腰长为5Cm,则它的周长为( ).
A.19 B.16 C.14 D.16或17
答案:B
知识点:等腰三角形的性质
解析:解答:等腰三角形的底边长为6Cm,腰长为5Cm,则周长为:6+5+5=16, 故B项正确.
分析:根据等腰三角形的性质可知边为5,5,6,则周长为16.
15.已知等腰三角形两边长分别为6Cm和12Cm,则底边长为( ),周长为( ). .
A.6,30 B.16,25 C.14,30 D.12,30
答案:A
知识点:等腰三角形的性质;三角形三边关系
解析:解答:等腰三角形的两条边长分别为6和12,分情况讨论 :(1)边为6.6.12,由三角形三边关系可知不能组成三角形.(2)6.12.12可组成三角形,则周长为:6+12+12=30. 故A项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即6.12.12,则周长为30
二.填空题
16.等腰三角形的周长为30,腰长是12,则底边长为 .
答案:6
知识点:等腰三角形的性质
解析:解答:等腰三角形的周长为30,腰长是12,则底边为:30—12-12=6
分析:根据已知条件可直接计算出底边的长度.
17.等腰三角形有两条边长为4和9,则该三角形的周长是( )
答案:22
知识点:等腰三角形的性质;三角形三边关系
解析:解答:等腰三角形的两条边长分别为4和9,分情况讨论 :(1)边为4.4.9,由三角形三边关系可知不能组成三角形.(2)4.9.9可组成三角形,则周长为:4+9+9=22.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即4.9.9,则周长为22Cm.
18.若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
答案:50° 或80°
知识点:等腰三角形性质;三角形的内角和
解析:解答:等腰三角形中有一个角等于50°,分情况讨论 :(1)顶角为50°;(2)底角为50°,则顶角为:180°-(50°+50°)=80°
分析:根据等腰三角形性质可知已知角可有两种情况,在根据三角形的内角和计算顶角的度数.
19.等腰三角形的底边长为5,周长是25,则腰长为_________.
答案:10
知识点:等腰三角形的性质
解析:解答:等腰三角形的底边长为6,周长是25,等腰三角形的腰长为10.
分析:结合已知条件利用等腰三角形的性质可直接计算出腰的长度.
若等腰三角形中顶角等于110°,则其它两个底角的度数( ).
答案:35°,35°
知识点:等腰三角形性质,三角形的内角和
解析:解答:已知等腰三角形的底角为110°,则(180°-110°)2=35°.
分析:结合已知条件利用等腰三角形性质可直接计算出所求角的度数.
三.解答题
21.如图,在△ABC中,∠BAD=∠B,∠EAC=∠C,若△ADE的周长是12,则BC的长是多少?
答案:解:∵∠BAD=∠B,∴BD=AD,∵∠EAC=∠C,∴AE=CE,
∵AD+DE+DE=12,∴BC=BD+DE+EC=12.
知识点:等腰三角形的判定
解析:解答:∠BAD=∠B,∴BD=AD,∵∠EAC=∠C,∴AE=CE,
∵AD+DE+DE=12Cm,∴BC=BD+DE+EC=12Cm
分析:结合图形,利用等腰三角形的判定,可所求出BC的长度..
22.如图,若∠BGD=35°,AK=GK,求∠A的度数.
答案:解:∵ AK=GK∴∠GAK=∠AGK,∵∠BGD=35°∴∠A=∠AGK=35°
知识点:等腰三角形的性质
解析:解答:∵AK=GK ∴∠GAK=∠AGK,∵∠BGD=35°∴∠GAK=∠AGK=35°
分析:结合图形,利用等腰三角形的性质,可所求出∠A的度数..
23.如图,△ABC中,AB=AC,点M.N分别在BC所在直线上,且AM=AN,BM=CN吗?说明理由
答案:解:BM=CN,理由:过点A作AD⊥MN于点D,∵AB=AC∴BD=CD,∵AM=AN,∴MD=ND,则BM=CN.
知识点:等腰三角形的性质(三线合一)
解析:解答:解:BM=CN,理由:过点A作AD⊥MN于点D,∵AB=AC∴BD=CD,∵AM=AN,∴MD=ND,则BM=CN.
分析:过点A作AD⊥MN于点D,利用等腰三角形的三线合一,易得BD=CD,MD=ND,再由等式的性质可得结论:BM=CN.
24.如图3,在△ABC中,已知AD是∠BAC的平分线,DE.DF分别垂直于AB.AC,垂足分别为E.F,且D是BC的中点,你认为线段EB与FC相等吗?如果相等,请说明理由.
答案:解:相等,理由:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,
在Rt△BED和Rt△CFD中,∵DE=DF,BD=DC,∴Rt△BED≌Rt△CFD(HL),∴EB=FC.
知识点:角平分线的性质;直角三角形全等的判定
解析:解答:解:相等,理由:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,
在Rt△BED和Rt△CFD中,∵DE=DF,BD=DC,∴Rt△BED≌Rt△CFD(HL),∴EB=FC.
分析:利用角平分线的性质,得DE=DF,再证Rt△BED≌Rt△CFD得到EB=FC.
25.如下图,在等腰ΔABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F.∠CAE=∠CBF吗?说明理由.
答案:解:相等,理由:∵△ABC是等腰三角形,CH是底边上的高线,∴AC=BC, ∠ACP=∠BCP,∵CP=CP, ∴△ACP≌△BCP, ∴∠CAP=∠CBP, 即∠CAE=∠CBF ,
知识点:等腰三角形的性质;三角形全等的判
解析:
解答:解:相等,理由:∵ΔABC是等腰三角形,CH是底边上的高线,∴AC=BC, ∠ACP
=∠BCP,∵CP=CP,∴△ACP≌△BCP,∴∠CAP=∠CBP, 即∠CAE=∠CBF
分析:利用等腰三角形的性质得AC=BC,∠ACP=∠BCP,再判定△ACP≌△BCP,即可得出∠CAE=∠CBF .
1
新人教版数学八年级上册
第十三章轴对称13.3.1等腰三角形课时练习
一.选择题
1.知等腰三角形的一个底角为40°,则这个等腰三角形的顶角为( )
A.40° B.100° C.40°或100° D.50°或70°
答案:B
知识点:等腰三角形的性质;三角形内角和定理
解析:解答:∵等腰三角形的一个底角为40°∴顶角为180°-(40°+40°)=100°,故B项正确.
分析:结合所给条件根据等腰三角形性质可得两底角和为80°,再根据三角形内角和定理可得顶角的度数.
2.如图, AB=AC ,BD=BC, 若∠A=50°,则∠ABD=度数是( )
A.15° B.20° C.25° D. 30°
答案:A
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵AB=AC, ∠A=50°∴∠ABC=∠ACB=65°,∵BD=BC,∴∠BDC=∠ACB=65°则∠DBC=50°, ∠ABD=∠ABC -∠DBC =15°,故A项正确.
分析:根据所给条件利用等腰三角形性质在△ABC可得∠ABC=∠ACB=65°,在△BCD可得∠BDC=∠ACB=65°,再三角形内角和定理得∠DBC=50°,则∠ABD=∠ABC -∠DBC =15°
试3.等腰三角形的两条边长分别为3,6,那么它的周长为( )
A.15 B.12 C.12或15 D.不能确定
答案:A
知识点:等腰三角形的性质;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为3,6分情况讨论 :(1)边为3.3.6,由三角形三边关系可知不能组成三角形.(2)3.6.6可组成三角形,则周长为:6+6+3=15. 故A项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即3.6.6,则周长为15.
4.已知等腰三角形的两条边长分别是2和4,则它的周长是 ( )
A.8 B.10 C.8或10 D.无法确定
答案:B
知识点:;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为2和4分情况讨论 :(1)边为2.2.4,由三角形三边关系可知不能组成三角形.(2)2.4.4可组成三角形,则周长为:2+4+4=10. 故B项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即2.4.4,则周长为10.
5.已知等腰三角形的两条边长分别为3和7,则它的周长为( )
A.10 B.13 C.17 D.13或17
答案:C
知识点:等腰三角形的性质;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为3和7分情况讨论 :(1)边为3.3.7,由三角形三边关系可知不能组成三角形.(2)3.7.7可组成三角形,则周长为:3+7+7=17. 故C项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即3.7.7,则周长为17.
6.等腰三角形的两边长是2和5,它的周长是( )
A.9 B.12 C.9或12 D.7
答案:B
知识点:等腰三角形的性质;三角形三边关系
解析:解答:∵等腰三角形的两条边长分别为2和5分情况讨论 :(1)边为2.2.5,由三角形三边关系可知不能组成三角形.(2)2.5.5可组成三角形,则周长为:2+5+5=12. 故B项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即2.5.5,则周长为12.
7.已知一个等腰三角形两内角的度数之比1:4,则这个等腰三角形顶角的度数为()
A.20°;B.120°;C.20°或120°;D.30°;
答案:C
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵等腰三角形的两内角的度数之比为1:4分情况讨论 :(1)顶角为x底角4X,则4X+4X+X =180°,X=20°;(2) 顶角为4X底角X,则4X+X+X =180°,x=30,°则顶角为120°, 故C项正确.
分析:根据等腰三角形性质可知顶角有两种情况,结合三角形三内角和可得顶角度数.
8.已知:如图△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=4则 BC 为( ).
A.9 B.10 C.12 D.7
答案:C
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵AB=AC,∠C=30°,∴∠B=∠C=30°,∠BAC=180°-30°-30°=120°,∵AB⊥AD,∴∠BAD=90°,∴∠DAC=120°-90°=30°=∠C,∴AD=DC=4,∵∠BAD=90°,∠B=30°,AD=4,∴BD=2AD=8,∴BC=4+8=12,故C项正确.
分析:根据三角形内角和定理定理和等腰三角形性质求出∠B.∠BAC度数,求∠DAC=∠C,求出DC,根据含30度角的直角三角形性质求出BD,即可求出答案
9.若等腰三角形的一个角是70° ,则其底角为 .
A.70° B.55° C.70° 或 55° D.30°
答案:C
知识点:等腰三角形性质;三角形内角和定理的定理
解析:解答:∵等腰三角形的一个角是70°,分情况讨论 :(1)顶角为70°,则底角为 55° (2) 底角70°,则顶角为40° 故C项正确.
分析:根据等腰三角形性质可知底角有两种情况,结合三角形三内角和可得顶角度数.
10.等腰三角形的顶角是,则它的一个底角的度数( )
A.70° B.55° C.70° 或 55° D.30°
答案:A
知识点:等腰三角形性质;三角形内角和定理
解析:解答:∵等腰三角形的顶角是,则底角70°故A项正确.
分析:根据等腰三角形性质可知两底角相等,结合三角形三内角和可得底角度数.
11.等腰三角形的底角是20°,则顶角的度数是( ). .
A.140° B.55° C.70° D.30°
答案:A
知识点:等腰三角形性质;三角形内角和定理
解析:解答:等腰三角形的底角是20°,顶角为140° 故A项正确.
分析:根据等腰三角形性质可知两底角相等,结合三角形三内角和可得顶角度数.
12.若等腰三角形中有一个角等于110°,则其它两个角的度数为( ).
A.70° B.110°和 70° C.35°和35° D.30°和70°
答案:C
知识点:等腰三角形性质;三角形内角和定理
解析:解答:等腰三角形的一个角是110°,其它两个角35°和35°,故C项正确.
分析:由等腰三角形性质可知有两个角相等,根据已知角的度数利用三角形三内角和可得其它两个角的度数.
13.若等腰三角形中有一个角等于50° ,则其它两个角的度数为()。
A.70° B.50°和 80 或 65°和65° C.65°和65° D.50°和 80°
答案:B
知识点:等腰三角形性质;三角形内角和定理
解析:解答:等腰三角形中有一个角等于50° ,分两种情况讨论:(1)50° 为底角,其它两个角的度数为50° 和 80°; (2)50° 为顶角,其它两个角的度数为65° 和65°. 故B项正确
分析:根据已知角的度数分两种情况讨论,利用三角形三内角和可得其它两个角的度数.
14.已知等腰三角形底边长为6Cm,腰长为5Cm,则它的周长为( ).
A.19 B.16 C.14 D.16或17
答案:B
知识点:等腰三角形的性质
解析:解答:等腰三角形的底边长为6Cm,腰长为5Cm,则周长为:6+5+5=16, 故B项正确.
分析:根据等腰三角形的性质可知边为5,5,6,则周长为16.
15.已知等腰三角形两边长分别为6Cm和12Cm,则底边长为( ),周长为( ). .
A.6,30 B.16,25 C.14,30 D.12,30
答案:A
知识点:等腰三角形的性质;三角形三边关系
解析:解答:等腰三角形的两条边长分别为6和12,分情况讨论 :(1)边为6.6.12,由三角形三边关系可知不能组成三角形.(2)6.12.12可组成三角形,则周长为:6+12+12=30. 故A项正确.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即6.12.12,则周长为30
二.填空题
16.等腰三角形的周长为30,腰长是12,则底边长为 .
答案:6
知识点:等腰三角形的性质
解析:解答:等腰三角形的周长为30,腰长是12,则底边为:30—12-12=6
分析:根据已知条件可直接计算出底边的长度.
17.等腰三角形有两条边长为4和9,则该三角形的周长是( )
答案:22
知识点:等腰三角形的性质;三角形三边关系
解析:解答:等腰三角形的两条边长分别为4和9,分情况讨论 :(1)边为4.4.9,由三角形三边关系可知不能组成三角形.(2)4.9.9可组成三角形,则周长为:4+9+9=22.
分析:根据等腰三角形的性质可知边有两种组成情况,结合三角形三边关系可得只有一组边可以组成三角形,即4.9.9,则周长为22Cm.
18.若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为( )
答案:50° 或80°
知识点:等腰三角形性质;三角形的内角和
解析:解答:等腰三角形中有一个角等于50°,分情况讨论 :(1)顶角为50°;(2)底角为50°,则顶角为:180°-(50°+50°)=80°
分析:根据等腰三角形性质可知已知角可有两种情况,在根据三角形的内角和计算顶角的度数.
19.等腰三角形的底边长为5,周长是25,则腰长为_________.
答案:10
知识点:等腰三角形的性质
解析:解答:等腰三角形的底边长为6,周长是25,等腰三角形的腰长为10.
分析:结合已知条件利用等腰三角形的性质可直接计算出腰的长度.
若等腰三角形中顶角等于110°,则其它两个底角的度数( ).
答案:35°,35°
知识点:等腰三角形性质,三角形的内角和
解析:解答:已知等腰三角形的底角为110°,则(180°-110°)2=35°.
分析:结合已知条件利用等腰三角形性质可直接计算出所求角的度数.
三.解答题
21.如图,在△ABC中,∠BAD=∠B,∠EAC=∠C,若△ADE的周长是12,则BC的长是多少?
答案:解:∵∠BAD=∠B,∴BD=AD,∵∠EAC=∠C,∴AE=CE,
∵AD+DE+DE=12,∴BC=BD+DE+EC=12.
知识点:等腰三角形的判定
解析:解答:∠BAD=∠B,∴BD=AD,∵∠EAC=∠C,∴AE=CE,
∵AD+DE+DE=12Cm,∴BC=BD+DE+EC=12Cm
分析:结合图形,利用等腰三角形的判定,可所求出BC的长度..
22.如图,若∠BGD=35°,AK=GK,求∠A的度数.
答案:解:∵ AK=GK∴∠GAK=∠AGK,∵∠BGD=35°∴∠A=∠AGK=35°
知识点:等腰三角形的性质
解析:解答:∵AK=GK ∴∠GAK=∠AGK,∵∠BGD=35°∴∠GAK=∠AGK=35°
分析:结合图形,利用等腰三角形的性质,可所求出∠A的度数..
23.如图,△ABC中,AB=AC,点M.N分别在BC所在直线上,且AM=AN,BM=CN吗?说明理由
答案:解:BM=CN,理由:过点A作AD⊥MN于点D,∵AB=AC∴BD=CD,∵AM=AN,∴MD=ND,则BM=CN.
知识点:等腰三角形的性质(三线合一)
解析:解答:解:BM=CN,理由:过点A作AD⊥MN于点D,∵AB=AC∴BD=CD,∵AM=AN,∴MD=ND,则BM=CN.
分析:过点A作AD⊥MN于点D,利用等腰三角形的三线合一,易得BD=CD,MD=ND,再由等式的性质可得结论:BM=CN.
24.如图3,在△ABC中,已知AD是∠BAC的平分线,DE.DF分别垂直于AB.AC,垂足分别为E.F,且D是BC的中点,你认为线段EB与FC相等吗?如果相等,请说明理由.
答案:解:相等,理由:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,
在Rt△BED和Rt△CFD中,∵DE=DF,BD=DC,∴Rt△BED≌Rt△CFD(HL),∴EB=FC.
知识点:角平分线的性质;直角三角形全等的判定
解析:解答:解:相等,理由:∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,∴DE=DF,
在Rt△BED和Rt△CFD中,∵DE=DF,BD=DC,∴Rt△BED≌Rt△CFD(HL),∴EB=FC.
分析:利用角平分线的性质,得DE=DF,再证Rt△BED≌Rt△CFD得到EB=FC.
25.如下图,在等腰ΔABC中,CH是底边上的高线,点P是线段CH上不与端点重合的任意一点,连结AP交BC于点E,连结BP交AC于点F.∠CAE=∠CBF吗?说明理由.
答案:解:相等,理由:∵△ABC是等腰三角形,CH是底边上的高线,∴AC=BC, ∠ACP=∠BCP,∵CP=CP, ∴△ACP≌△BCP, ∴∠CAP=∠CBP, 即∠CAE=∠CBF ,
知识点:等腰三角形的性质;三角形全等的判
解析:
解答:解:相等,理由:∵ΔABC是等腰三角形,CH是底边上的高线,∴AC=BC, ∠ACP
=∠BCP,∵CP=CP,∴△ACP≌△BCP,∴∠CAP=∠CBP, 即∠CAE=∠CBF
分析:利用等腰三角形的性质得AC=BC,∠ACP=∠BCP,再判定△ACP≌△BCP,即可得出∠CAE=∠CBF .
1
