新人教版数学八年级上册第十三章轴对称13.4《课题学习 最短路径问题》课时练习.doc
文档属性
| 名称 | 新人教版数学八年级上册第十三章轴对称13.4《课题学习 最短路径问题》课时练习.doc |
|
|
| 格式 | doc | ||
| 文件大小 | 560.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-19 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新人教版数学八年级上册13.4课题学习 最短路径问题课时练习
一、选择题(共15小题)
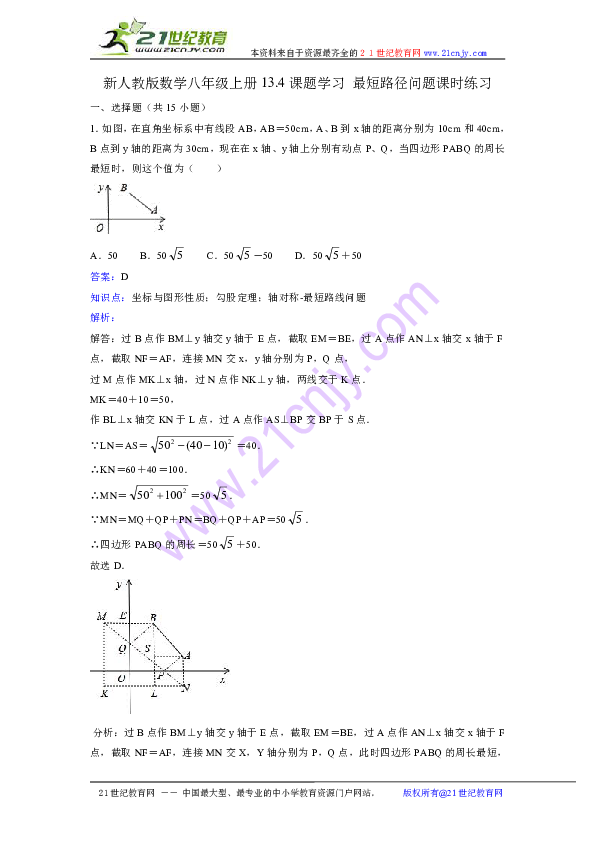
1.如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为( )
A.50 B.50 C.50-50 D.50+50
答案:D
知识点:坐标与图形性质;勾股定理;轴对称-最短路线问题
解析:
解答:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交x,y轴分别为P,Q点,
过M点作MK⊥x轴,过N点作NK⊥y轴,两线交于K点.
MK=40+10=50,
作BL⊥x轴交KN于L点,过A点作AS⊥BP交BP于S点.
∵LN=AS==40.
∴KN=60+40=100.
∴MN==50.
∵MN=MQ+QP+PN=BQ+QP+AP=50.
∴四边形PABQ的周长=50+50.
故选D.
分析:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交X,Y轴分别为P,Q点,此时四边形PABQ的周长最短,根据题目所给的条件可求出周长.
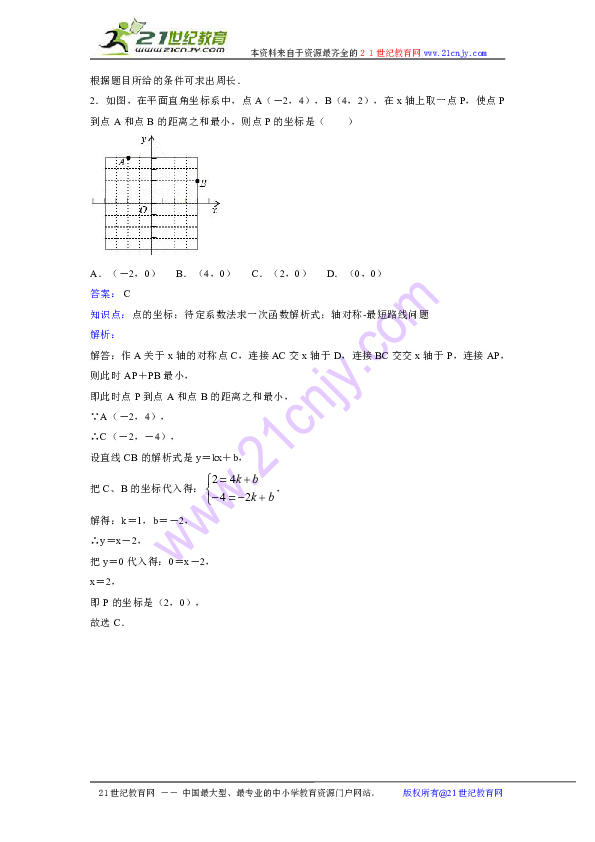
2.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A.(-2,0) B.(4,0) C.(2,0) D.(0,0)
答案: C
知识点:点的坐标;待定系数法求一次函数解析式;轴对称-最短路线问题
解析:
解答:作A关于x轴的对称点C,连接AC交x轴于D,连接BC交交x轴于P,连接AP,
则此时AP+PB最小,
即此时点P到点A和点B的距离之和最小,
∵A(-2,4),
∴C(-2,-4),
设直线CB的解析式是y=kx+b,
把C、B的坐标代入得:,
解得:k=1,b=-2,
∴y=x-2,
把y=0代入得:0=x-2,
x=2,
即P的坐标是(2,0),
故选C.
分析:作A关于x轴的对称点C,连接AC交x轴于D,连接BC交交x轴于P,连接AP,此时点P到点A和点B的距离之和最小,求出C(的坐标,设直线CB的解析式是y=kx+b,把C、B的坐标代入求出解析式是y=x-2,把y=0代入求出x即可.
3.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( ).
A.15° B.22.5° C.30° D.45°
答案:C
知识点:等边三角形的性质; 轴对称-最短路线问题
解析:
解答:
过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°,
故选C.
分析:过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可求出答案.
4.如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( ).
A. B. 6 C. D.
答案:D
知识点:等边三角形的判定与性质;轴对称-最短路线问题
解析:
解答:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,
连接OD,OE,
∵P、D关于OA对称,
∴OD=OP,PM=DM,
同理OE=OP,PN=EN,
∴OD=OE=OP=
∵P、D关于OA对称,
∴OA⊥PD,
∵OD=OP,
∴∠DOA=∠POA,
同理∠POB=∠EOB,
∴∠DOE=2∠AOB2×30°═60°,
∵OD=OE=,
∴△DOE是等边三角形,
∴DE=,
即△PMN的周长是PM+MN+PN=DM+MN+EN=DE=,
故选D.
分析:根据题意画出符合条件的图形,求出OD=OE=OP,∠DOE=60°,得出等边三角形DOE,求出DE=,求出△PMN的周长=DE,即可求出答案.
5.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( ).
A. (,-4) B. (,0) C. (,0) D. (,0)
答案:C
知识点:坐标与图形性质;轴对称-最短路线问题;待定系数法求一次函数解析式
解析:
解答:∵PM+PN最短,
∴M、P、N三点共线,
∵M(3,5),N(1,-1),
∴设解析式为y=kx+b,
把M(3,5),N(1,-1)分别代入解析式得,
,
解得,
其解析式为y=3x-4.
当y=0时,x=.
故P点坐标为(,0).
故选C.
分析:若PM+PN最短,则M、P、N三点共线,根据M、N的坐标,求出MN的解析式,再求出与x轴的交点即可.
6.已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( ).
A. 30° B. 45° C. 60° D. 90°
答案:A
知识点:等边三角形的判定与性质; 轴对称-最短路线问题
解析:
解答:如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=OP=2,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,
∴OC=OD=CD=2,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故选A.
分析:设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=2可求出α的度数.
7.直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. B.
C. D.
答案:D
知识点:轴对称-最短路线问题
解析:
解答:作点P关于直线L的对称点P′,连接QP′交直线L于M.
根据两点之间,线段最短,可知选项D铺设的管道,则所需管道最短.
故选D.
分析: 利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
8.已知两点A(3,2)和B(1,-2),点P在y轴上且使AP+BP最短,则点P的坐标是( ).
A. (0,) B. (0,) C. (0,-1) D. (0,)
答案:C
知识点:点的坐标; 轴对称-最短路线问题;待定系数法求一次函数解析式
解析:
解答:根据已知条件,点A关于y轴的对称点A′为(-3,2).
设过A′B的解析式为y=kx+b,则-3k+b=2;k+b=-2.
解得k=-1,b=-1
那么此函数解析式为y=-x-1.与y轴的交点是(0,-1),此点就是所求的点P.
故选C.
分析:根据已知条件和两点间线段最短,可知P点是“其中一点关于y轴的对称点与另一点的连线和y轴的交点.
9.在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, m)(m为非负数),则CA+CB的最小值是( ).
A. 6 B. C. D. 5
答案:C
知识点: 轴对称-最短路线问题;待定系数法求一次函数解析式;两条直线相交或平行问题
解析:
解答:如图所示:
∵点C的坐标为(m, m)(m为非负数),
∴点C的坐标所在直线为y=x,
点A关于直线y=x的对称点的坐标为A′,则AA′所在直线为y=x+b,
把点A的坐标( 2,0 )代入得×2+b=0,
解得b=.
故AA′所在直线为y=x+.
联立C的坐标所在直线和AA′所在直线可得,
解得,
∴C的坐标所在直线和AA′所在直线的交点M的坐标为(,),
∴点A关于直线y=x的对称点的坐标为(-1,),
∴A′B===2,即CA+CB的最小值.
故选C.
分析:分别得到点C的坐标所在直线,点A关于点C的坐标所在直线的对称点的坐标A′所在直线AA′的解析式,求得两条直线的交点,进一步得到A′点的坐标,再根据两点间的距离公式即可求解.
10.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ).
A. 3 B. 4 C. 5 D. 6
答案:B
知识点:三角形的角平分线、中线和高; 轴对称-最短路线问题;全等三角形的判定与性质
解析:
解答:如图,在AC上截取AE=AN,连接BE.
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中,,
∴△AME≌△AMN(SAS),
∴ME=MN.
∴BM+MN=BM+ME≥BE.
∵BM+MN有最小值.
当BE是点B到直线AC的距离时,BE⊥AC,
又AB=4,∠BAC=45°,此时,△ABE为等腰直角三角形,
∴BE=4,
即BE取最小值为4,
∴BM+MN的最小值是4.
故答案为:B.
分析:从已知条件结合图形认真思考,通过构造全等三角形,利用三角形的三边的关系确定线段和的最小值.
11.如图,锐角三角形ABC中,∠C=45°,N为BC上一点,NC=5,BN=2,M为边AC上的一个动点,则BM+MN的最小值是( ).
A. B. C. D.
答案:C
知识点:三角形相关概念;勾股定理; 轴对称-最短路线问题
解析:
解答:如图所示,
先作点N关于AC的对称点N′,由两点之间线段最短可知BN′即为BM+MN的最小值,
根据对称的性质可知N′C=NC=5,∠ACB=∠ACN′=45°,即∠BCN′=90°,
在Rt△BCN′中,BN′===.
故答案为:C.
分析:先作点N关于AC的对称点N′,由两点之间线段最短可知BN′即为BM+MN的最小值,根据对称的性质可知N′C=NC=5,∠BCN′=90°,再利用勾股定理即可求出BN′的长.
12.加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于( )米.
A. 8 B. 9 C. 6 D. 7
答案:D
知识点:轴对称-最短路线问题;三角形的三边关系
解析:
解答:当A、B、P三点不在同一直线上时,
此时三点构成三角形.
∵两边AP与BP的差小于第三边AB.
∴A、B、P在同一直线上,
∴P到A的距离与P到B的距离之差最大,
∴这个差就是AB的长,
故答案为:D.
分析:当ABP构成三角形时,AP与BP的差小于第三边AB,所以当ABP在同一直线上时,PA与PB之差最大=AB=7.
13.如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为( ).
A. B. 10 C. 12 D. 13
答案:A
知识点:轴对称-最短路线问题;等腰三角形的性质;勾股定理
解析:
解答:
作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,由勾股定理得:AD==12,
∴S△ABC=×BC×AD=×AB×CN,
∴CN===,
∵E关于AD的对称点M,
∴EF=FM,
∴CF+EF=CF+FM=CM,
根据垂线段最短得出:CM≥CN,
即CF+EF≥,
即CF+EF的最小值是,
故答案为:A.
分析:作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,根据三线合一定理求出BD的长和AD⊥BC,根据勾股定理求出AD,根据三角形面积公式求出CN,根据对称性质求出CF+EF=CM,根据垂线段最短得出CF+EF≥,即可得出答案.
14.如图,Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是( ).
A. B. 4 C. D. 5
答案:C
知识点:轴对称-最短路线问题;等腰三角形的性质
解析:
解答:如图,连接BE,
则BE就是PA+PE的最小值,
∵Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,
∴CE=2cm,
∴BE==,
∴PA+PE的最小值是.
故答案为:C.
分析:要求PA+PE的最小值,PA,PE不能直接求,可考虑通过作辅助线转化PA,PE的值,从而找出其最小值求解.
15.已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走( )米.
A. 1100 B. 1200 C. 1300 D. 1400
答案:C
知识点:轴对称-最短路线问题;勾股定理
解析:
解答:点B关于CD的对称点E,
由对称的性质可知,BD=ED,∠EDM=∠MDB,DM=DM,
∴△MDE≌△MDB,
∴BM=ME,BM+AM=ME+AM=AE,
即AE为牧童要走的最短路程.
∵EN=CD=500米,AN=NC+AC=700+500=1200米,
∴在Rt△ANE中,AE===1300米.
故牧童至少要走1300米.
分析:在CD边上找一点M,使AM和BM的和最小,延长BD到E点,使BD=DE,连接AE交CD边于点M,过点E作EN⊥AC于点N,则AE为所求的长即牧童最少要走的距离.
二、填空题(共5小题)
1.如图,已知AB⊥AD,CD⊥AD,垂足分别为A、D,AD=6,AB=5,CD=3,P是线段AD上的一个动点,设AP=x,DP=y,,则a的最小值是______.
答案:10
知识点:相似三角形的判定与性质;轴对称-最短路线问题
解析:
解答:由题意可得,当BPC三点在同一直线时,a的值最小.
则△ABP∽△DCP,
x=,y=,
则a的最小值是10.
分析:首先确定当BPC三点在同一直线时,a的值最小.然后根据相似三角形的性质计算.
2.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为_____.
答案:100°
知识点:多边形内角与外角;三角形相关概念;轴对称-最短路线问题
解析:
解答:如图,作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°-∠MON=180°-40°=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=140°-40°=100°.
故答案为:100°.
分析:作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,再由四边形内和定理即可求出答案.
3.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是_____.
答案:
知识点:等边三角形的性质;勾股定理;轴对称-最短路线问题
解析:
解答:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,连接CE,
此时DE+CE=DE+EC′=DC′的值最小.
连接BC′,由对称性可知∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=2,
∵D是BC边的中点,
∴BD=1,
根据勾股定理可得DC′==.
故答案为:.
分析:首先确定DC′=DE+EC′=DE+CE的值最小.然后根据勾股定理计算.
4.已知:如图所示,M(3,2),N(1,-1).点P在y轴上使PM+PN最短,则P点坐标为_________.
答案:(0,-)
知识点:点的坐标;一次函数的应用;轴对称-最短路线问题
解析:
解答:根据题意画出图形,找出点N关于y轴的对称点N′,连接MN′,与y轴交点为所求的点P,
∵N(1,-1),
∴N′(-1,-1),
设直线MN′的解析式为y=kx+b,把M(3,2),N′(-1,-1)代入得:
,
解得,
所以y=x-,
令x=0,求得y=-,
则点P坐标为(0,-).
分析:找出点N关于y轴的对称点,连接M与对称点,与y轴的交点为P点,根据两点之间,线段最短得到此时点P在y轴上,且能使PM+PN最短.根据关于y轴对称点的特点,找出N对称点的坐标,设出直线MP的方程,把N的对称点的坐标和M的坐标代入即可确定出直线MP的方程,然后令x=0求出直线与y轴的交点,写出交点坐标即为点P的坐标.
5.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,则(1)EF=____;(2)若D是BC边上一动点,则△EFD的周长最小值是____.
答案:2;2+2
知识点:勾股定理;轴对称-最短路线问题;三角形中位线定理
解析:
解答:(1)∵E是AB边的中点,F是AC边的中点,
∴EF为△ABC的中位线,
∵BC=4,
∴EF=BC=×4=2;
(2)延长FC到P,使FC=PC,连接EP交BC于D,连接ED、FD,此时ED+FD最小,即△EDF的周长最小,
∵EF为△ABC的中位线,
∴EF∥BC,
∵∠C=90°,
∴∠EFC=90°,FC=PC=AC=2,
∵在Rt△EFP中,EP===2,
∴△EDF的周长为:EF+FD+ED=2+ED+PD=2+EP=2+2,
故答案为:2;2+2.
分析:(1)根据E是AB边的中点,F是AC边的中点可以得到EF为三角形的中位线,根据中位线定理求得EF的长即可;
(2)根据对称点的性质,延长FC到P,使FC=PC,连接EP交BC于D,连接ED、FD,此时ED+FD最小,即△EDF的周长最小,求出EP长,即可求出答案.
三、解答题(共6小题)
1.已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
答案:(1)见解析;(2)AM+AN=BM+BN
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:(1)如图所示.
画法:
①作点M关于射线OP的对称点M',
②连接M'N交OP于点A.
③作点N关于射线OQ的对称点N',
④连接N'M交OQ于点B.
(2)答:AM+AN与BM+BN的大小关系是:AM+AN=BM+BN.
分析:(1)分别作出点M关于射线OP的对称点M',点N关于射线OQ的对称点N',连接M'N、N'M即可求出答案;
(2)根据轴对称性质求出即可.
2.某大型农场拟在公路L旁修建一个农产品储藏、加工厂,将该农场两个规模相同的水果生产基地A、B的水果集中进行储藏和技术加工,以提高经济效益.请你在图中标明加工厂所在的位置C,使A、B两地到加工厂C的运输路程之和最短.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:如图
分析:作A关于直线L的对称点E,连接BE交直线L于C,则C为所求.
3.如图,△ABC的边AB、AC上分别有定点M、N,请在BC边上找一点P,使得△PMN的周长最短. (写出作法,保留作图痕迹)
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:①作点N关于BC的对称点N′,连接MN′交BC于点P,
②由对称的性质可知PN=PN′,故PN+PM=MN′,
③由两点之间线段最短可知,△PMN的最短周长即为MN′+MN.
分析:作点N关于BC的对称点N′,连接MN′交BC于点P,由两点之间线段最短可知P点即为所求点.
4.在某一地方,有条小河和草地,一天某牧民的计划是从A处的牧场牵着一只马到草地牧马,再到小河饮马,你能为他设计一条最短的路线吗?(在N上任意一点即可牧马,M上任意一点即可饮马.)(保留作图痕迹,需要证明)
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:沿AC-CD-DB路线走是最短的路线如图(1)所示:
证明:在ON上任意取一点T,在OM上任意取一点R,连接FR、BR、RT、ET、AT,
∵A、E关于ON对称,
∴AC=EC,
同理BD=FD,FR=BR,AT=ET,
∴AC+CD+DB=EC+CD+FD=EF,
AT+TR+BR=ET+TR+FR,
∵ET+TR+FR>EF,
∴AC+CD+DB<AT+TR+BR,
即沿AC-CD-DB路线走是最短的路线.
分析:作A关于ON的对称点E,B关于OM的对称点F,连接EF交ON于C,交OM于D,连接AC、BD,即可得出答案;
根据对称点推出AC=EC,BD=FD,FR=BR,AT=ET,根据两点之间线段最短即可求出答案.
5.已知:如图所示,
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.
答案:见解析
知识点:轴对称-最短路线问题;关于x轴、y轴对称的点的坐标;作图-轴对称变换
解析:
解答:(1)
分别作A、B、C的对称点,A′、B′、C′,由三点的位置可知:
A′(-1,2),B′(-3,1),C′(-4,3)
(2)先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,
(或找出A点关于x轴对称的点A″(1,-2),连接A″C交x轴于点P)则P点即为所求点.
分析:(1)根据轴对称的性质分别作出A、B、C三点关于y轴的对称点A′、B′、C′,分别连接各点即可;
(2)先找出C先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,则点p即为所求点.
6.作图题:(写出作法,保留作图痕迹)
M、N为△ABC为AB、AC上的两个定点,请你在BC边上找一点P,使PMN周长最小?
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:作法:(1)作M关于BC的对称点M’
(2)连接M’N交BC于P点
(3)连线MP,则△PMN周长最小 P为所求作的点.
分析:由于△PMN的周长=PM+PN+MN,而MN是定值,故只需在BC上找一点P,使PM+PN最小.如果设M关于BC的对称点为M,使PM,+PN最小.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新人教版数学八年级上册13.4课题学习 最短路径问题课时练习
一、选择题(共15小题)
1.如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为( )
A.50 B.50 C.50-50 D.50+50
答案:D
知识点:坐标与图形性质;勾股定理;轴对称-最短路线问题
解析:
解答:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交x,y轴分别为P,Q点,
过M点作MK⊥x轴,过N点作NK⊥y轴,两线交于K点.
MK=40+10=50,
作BL⊥x轴交KN于L点,过A点作AS⊥BP交BP于S点.
∵LN=AS==40.
∴KN=60+40=100.
∴MN==50.
∵MN=MQ+QP+PN=BQ+QP+AP=50.
∴四边形PABQ的周长=50+50.
故选D.
分析:过B点作BM⊥y轴交y轴于E点,截取EM=BE,过A点作AN⊥x轴交x轴于F点,截取NF=AF,连接MN交X,Y轴分别为P,Q点,此时四边形PABQ的周长最短,根据题目所给的条件可求出周长.
2.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A.(-2,0) B.(4,0) C.(2,0) D.(0,0)
答案: C
知识点:点的坐标;待定系数法求一次函数解析式;轴对称-最短路线问题
解析:
解答:作A关于x轴的对称点C,连接AC交x轴于D,连接BC交交x轴于P,连接AP,
则此时AP+PB最小,
即此时点P到点A和点B的距离之和最小,
∵A(-2,4),
∴C(-2,-4),
设直线CB的解析式是y=kx+b,
把C、B的坐标代入得:,
解得:k=1,b=-2,
∴y=x-2,
把y=0代入得:0=x-2,
x=2,
即P的坐标是(2,0),
故选C.
分析:作A关于x轴的对称点C,连接AC交x轴于D,连接BC交交x轴于P,连接AP,此时点P到点A和点B的距离之和最小,求出C(的坐标,设直线CB的解析式是y=kx+b,把C、B的坐标代入求出解析式是y=x-2,把y=0代入求出x即可.
3.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为( ).
A.15° B.22.5° C.30° D.45°
答案:C
知识点:等边三角形的性质; 轴对称-最短路线问题
解析:
解答:
过E作EM∥BC,交AD于N,
∵AC=4,AE=2,
∴EC=2=AE,
∴AM=BM=2,
∴AM=AE,
∵AD是BC边上的中线,△ABC是等边三角形,
∴AD⊥BC,
∵EM∥BC,
∴AD⊥EM,
∵AM=AE,
∴E和M关于AD对称,
连接CM交AD于F,连接EF,
则此时EF+CF的值最小,
∵△ABC是等边三角形,
∴∠ACB=60°,AC=BC,
∵AM=BM,
∴∠ECF=∠ACB=30°,
故选C.
分析:过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可求出答案.
4.如图,∠AOB=30°,内有一点P且OP=,若M、N为边OA、OB上两动点,那么△PMN的周长最小为( ).
A. B. 6 C. D.
答案:D
知识点:等边三角形的判定与性质;轴对称-最短路线问题
解析:
解答:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB于N,连接PM,PN,则此时△PMN的周长最小,
连接OD,OE,
∵P、D关于OA对称,
∴OD=OP,PM=DM,
同理OE=OP,PN=EN,
∴OD=OE=OP=
∵P、D关于OA对称,
∴OA⊥PD,
∵OD=OP,
∴∠DOA=∠POA,
同理∠POB=∠EOB,
∴∠DOE=2∠AOB2×30°═60°,
∵OD=OE=,
∴△DOE是等边三角形,
∴DE=,
即△PMN的周长是PM+MN+PN=DM+MN+EN=DE=,
故选D.
分析:根据题意画出符合条件的图形,求出OD=OE=OP,∠DOE=60°,得出等边三角形DOE,求出DE=,求出△PMN的周长=DE,即可求出答案.
5.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为( ).
A. (,-4) B. (,0) C. (,0) D. (,0)
答案:C
知识点:坐标与图形性质;轴对称-最短路线问题;待定系数法求一次函数解析式
解析:
解答:∵PM+PN最短,
∴M、P、N三点共线,
∵M(3,5),N(1,-1),
∴设解析式为y=kx+b,
把M(3,5),N(1,-1)分别代入解析式得,
,
解得,
其解析式为y=3x-4.
当y=0时,x=.
故P点坐标为(,0).
故选C.
分析:若PM+PN最短,则M、P、N三点共线,根据M、N的坐标,求出MN的解析式,再求出与x轴的交点即可.
6.已知∠AOB的大小为α,P是∠AOB内部的一个定点,且OP=2,点E、F分别是OA、OB上的动点,若△PEF周长的最小值等于2,则α=( ).
A. 30° B. 45° C. 60° D. 90°
答案:A
知识点:等边三角形的判定与性质; 轴对称-最短路线问题
解析:
解答:如图,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.
连接OC,OD,PE,PF.
∵点P与点C关于OA对称,
∴OA垂直平分PC,
∴∠COA=∠AOP,PE=CE,OC=OP,
同理,可得∠DOB=∠BOP,PF=DF,OD=OP.
∴∠COA+∠DOB=∠AOP+∠BOP=∠AOB=α,OC=OD=OP=2,
∴∠COD=2α.
又∵△PEF的周长=PE+EF+FP=CE+EF+FD=CD=2,
∴OC=OD=CD=2,
∴△COD是等边三角形,
∴2α=60°,
∴α=30°.
故选A.
分析:设点P关于OA的对称点为C,关于OB的对称点为D,当点E、F在CD上时,△PEF的周长为PE+EF+FP=CD,此时周长最小,根据CD=2可求出α的度数.
7.直线L是一条河,P,Q是两个村庄.欲在L上的某处修建一个水泵站,向P,Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( ).
A. B.
C. D.
答案:D
知识点:轴对称-最短路线问题
解析:
解答:作点P关于直线L的对称点P′,连接QP′交直线L于M.
根据两点之间,线段最短,可知选项D铺设的管道,则所需管道最短.
故选D.
分析: 利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.
8.已知两点A(3,2)和B(1,-2),点P在y轴上且使AP+BP最短,则点P的坐标是( ).
A. (0,) B. (0,) C. (0,-1) D. (0,)
答案:C
知识点:点的坐标; 轴对称-最短路线问题;待定系数法求一次函数解析式
解析:
解答:根据已知条件,点A关于y轴的对称点A′为(-3,2).
设过A′B的解析式为y=kx+b,则-3k+b=2;k+b=-2.
解得k=-1,b=-1
那么此函数解析式为y=-x-1.与y轴的交点是(0,-1),此点就是所求的点P.
故选C.
分析:根据已知条件和两点间线段最短,可知P点是“其中一点关于y轴的对称点与另一点的连线和y轴的交点.
9.在平面直角坐标系中,点A、B的坐标分别为( 2,0 ),(4,0),点C的坐标为(m, m)(m为非负数),则CA+CB的最小值是( ).
A. 6 B. C. D. 5
答案:C
知识点: 轴对称-最短路线问题;待定系数法求一次函数解析式;两条直线相交或平行问题
解析:
解答:如图所示:
∵点C的坐标为(m, m)(m为非负数),
∴点C的坐标所在直线为y=x,
点A关于直线y=x的对称点的坐标为A′,则AA′所在直线为y=x+b,
把点A的坐标( 2,0 )代入得×2+b=0,
解得b=.
故AA′所在直线为y=x+.
联立C的坐标所在直线和AA′所在直线可得,
解得,
∴C的坐标所在直线和AA′所在直线的交点M的坐标为(,),
∴点A关于直线y=x的对称点的坐标为(-1,),
∴A′B===2,即CA+CB的最小值.
故选C.
分析:分别得到点C的坐标所在直线,点A关于点C的坐标所在直线的对称点的坐标A′所在直线AA′的解析式,求得两条直线的交点,进一步得到A′点的坐标,再根据两点间的距离公式即可求解.
10.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ).
A. 3 B. 4 C. 5 D. 6
答案:B
知识点:三角形的角平分线、中线和高; 轴对称-最短路线问题;全等三角形的判定与性质
解析:
解答:如图,在AC上截取AE=AN,连接BE.
∵∠BAC的平分线交BC于点D,
∴∠EAM=∠NAM,
在△AME与△AMN中,,
∴△AME≌△AMN(SAS),
∴ME=MN.
∴BM+MN=BM+ME≥BE.
∵BM+MN有最小值.
当BE是点B到直线AC的距离时,BE⊥AC,
又AB=4,∠BAC=45°,此时,△ABE为等腰直角三角形,
∴BE=4,
即BE取最小值为4,
∴BM+MN的最小值是4.
故答案为:B.
分析:从已知条件结合图形认真思考,通过构造全等三角形,利用三角形的三边的关系确定线段和的最小值.
11.如图,锐角三角形ABC中,∠C=45°,N为BC上一点,NC=5,BN=2,M为边AC上的一个动点,则BM+MN的最小值是( ).
A. B. C. D.
答案:C
知识点:三角形相关概念;勾股定理; 轴对称-最短路线问题
解析:
解答:如图所示,
先作点N关于AC的对称点N′,由两点之间线段最短可知BN′即为BM+MN的最小值,
根据对称的性质可知N′C=NC=5,∠ACB=∠ACN′=45°,即∠BCN′=90°,
在Rt△BCN′中,BN′===.
故答案为:C.
分析:先作点N关于AC的对称点N′,由两点之间线段最短可知BN′即为BM+MN的最小值,根据对称的性质可知N′C=NC=5,∠BCN′=90°,再利用勾股定理即可求出BN′的长.
12.加油站A和商店B在马路MN的同一侧(如图),A到MN的距离大于B到MN的距离,AB=7米,一个行人P在马路MN上行走,问:当P到A的距离与P到B的距离之差最大时,这个差等于( )米.
A. 8 B. 9 C. 6 D. 7
答案:D
知识点:轴对称-最短路线问题;三角形的三边关系
解析:
解答:当A、B、P三点不在同一直线上时,
此时三点构成三角形.
∵两边AP与BP的差小于第三边AB.
∴A、B、P在同一直线上,
∴P到A的距离与P到B的距离之差最大,
∴这个差就是AB的长,
故答案为:D.
分析:当ABP构成三角形时,AP与BP的差小于第三边AB,所以当ABP在同一直线上时,PA与PB之差最大=AB=7.
13.如图,△ABC中,AB=AC=13,BC=10,AD是BC边上的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为( ).
A. B. 10 C. 12 D. 13
答案:A
知识点:轴对称-最短路线问题;等腰三角形的性质;勾股定理
解析:
解答:
作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,
∵AB=AC=13,BC=10,AD是BC边上的中线,
∴BD=DC=5,AD⊥BC,AD平分∠BAC,
∴M在AB上,
在Rt△ABD中,由勾股定理得:AD==12,
∴S△ABC=×BC×AD=×AB×CN,
∴CN===,
∵E关于AD的对称点M,
∴EF=FM,
∴CF+EF=CF+FM=CM,
根据垂线段最短得出:CM≥CN,
即CF+EF≥,
即CF+EF的最小值是,
故答案为:A.
分析:作E关于AD的对称点M,连接CM交AD于F,连接EF,过C作CN⊥AB于N,根据三线合一定理求出BD的长和AD⊥BC,根据勾股定理求出AD,根据三角形面积公式求出CN,根据对称性质求出CF+EF=CM,根据垂线段最短得出CF+EF≥,即可得出答案.
14.如图,Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,在CD上找一点P,使PA+PE最小,则这个最小值是( ).
A. B. 4 C. D. 5
答案:C
知识点:轴对称-最短路线问题;等腰三角形的性质
解析:
解答:如图,连接BE,
则BE就是PA+PE的最小值,
∵Rt△ABC中,AC=BC=4,点D,E分别是AB,AC的中点,
∴CE=2cm,
∴BE==,
∴PA+PE的最小值是.
故答案为:C.
分析:要求PA+PE的最小值,PA,PE不能直接求,可考虑通过作辅助线转化PA,PE的值,从而找出其最小值求解.
15.已知,如图,一牧童在A处牧马,牧童家在B处,A,B两处距河岸的距离AC,BD的长分别为700米,500米,且CD的距离为500米,天黑前牧童从A点将马牵到河边去饮水后,再赶回家,那么牧童最少要走( )米.
A. 1100 B. 1200 C. 1300 D. 1400
答案:C
知识点:轴对称-最短路线问题;勾股定理
解析:
解答:点B关于CD的对称点E,
由对称的性质可知,BD=ED,∠EDM=∠MDB,DM=DM,
∴△MDE≌△MDB,
∴BM=ME,BM+AM=ME+AM=AE,
即AE为牧童要走的最短路程.
∵EN=CD=500米,AN=NC+AC=700+500=1200米,
∴在Rt△ANE中,AE===1300米.
故牧童至少要走1300米.
分析:在CD边上找一点M,使AM和BM的和最小,延长BD到E点,使BD=DE,连接AE交CD边于点M,过点E作EN⊥AC于点N,则AE为所求的长即牧童最少要走的距离.
二、填空题(共5小题)
1.如图,已知AB⊥AD,CD⊥AD,垂足分别为A、D,AD=6,AB=5,CD=3,P是线段AD上的一个动点,设AP=x,DP=y,,则a的最小值是______.
答案:10
知识点:相似三角形的判定与性质;轴对称-最短路线问题
解析:
解答:由题意可得,当BPC三点在同一直线时,a的值最小.
则△ABP∽△DCP,
x=,y=,
则a的最小值是10.
分析:首先确定当BPC三点在同一直线时,a的值最小.然后根据相似三角形的性质计算.
2.已知如图所示,∠MON=40°,P为∠MON内一点,A为OM上一点,B为ON上一点,则当△PAB的周长取最小值时,∠APB的度数为_____.
答案:100°
知识点:多边形内角与外角;三角形相关概念;轴对称-最短路线问题
解析:
解答:如图,作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°-∠MON=180°-40°=140°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°-∠P1PP2=40°,
∴∠APB=140°-40°=100°.
故答案为:100°.
分析:作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,再由四边形内和定理即可求出答案.
3.如图,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是_____.
答案:
知识点:等边三角形的性质;勾股定理;轴对称-最短路线问题
解析:
解答:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于E,连接CE,
此时DE+CE=DE+EC′=DC′的值最小.
连接BC′,由对称性可知∠C′BE=∠CBE=45°,
∴∠CBC′=90°,
∴BC′⊥BC,∠BCC′=∠BC′C=45°,
∴BC=BC′=2,
∵D是BC边的中点,
∴BD=1,
根据勾股定理可得DC′==.
故答案为:.
分析:首先确定DC′=DE+EC′=DE+CE的值最小.然后根据勾股定理计算.
4.已知:如图所示,M(3,2),N(1,-1).点P在y轴上使PM+PN最短,则P点坐标为_________.
答案:(0,-)
知识点:点的坐标;一次函数的应用;轴对称-最短路线问题
解析:
解答:根据题意画出图形,找出点N关于y轴的对称点N′,连接MN′,与y轴交点为所求的点P,
∵N(1,-1),
∴N′(-1,-1),
设直线MN′的解析式为y=kx+b,把M(3,2),N′(-1,-1)代入得:
,
解得,
所以y=x-,
令x=0,求得y=-,
则点P坐标为(0,-).
分析:找出点N关于y轴的对称点,连接M与对称点,与y轴的交点为P点,根据两点之间,线段最短得到此时点P在y轴上,且能使PM+PN最短.根据关于y轴对称点的特点,找出N对称点的坐标,设出直线MP的方程,把N的对称点的坐标和M的坐标代入即可确定出直线MP的方程,然后令x=0求出直线与y轴的交点,写出交点坐标即为点P的坐标.
5.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,则(1)EF=____;(2)若D是BC边上一动点,则△EFD的周长最小值是____.
答案:2;2+2
知识点:勾股定理;轴对称-最短路线问题;三角形中位线定理
解析:
解答:(1)∵E是AB边的中点,F是AC边的中点,
∴EF为△ABC的中位线,
∵BC=4,
∴EF=BC=×4=2;
(2)延长FC到P,使FC=PC,连接EP交BC于D,连接ED、FD,此时ED+FD最小,即△EDF的周长最小,
∵EF为△ABC的中位线,
∴EF∥BC,
∵∠C=90°,
∴∠EFC=90°,FC=PC=AC=2,
∵在Rt△EFP中,EP===2,
∴△EDF的周长为:EF+FD+ED=2+ED+PD=2+EP=2+2,
故答案为:2;2+2.
分析:(1)根据E是AB边的中点,F是AC边的中点可以得到EF为三角形的中位线,根据中位线定理求得EF的长即可;
(2)根据对称点的性质,延长FC到P,使FC=PC,连接EP交BC于D,连接ED、FD,此时ED+FD最小,即△EDF的周长最小,求出EP长,即可求出答案.
三、解答题(共6小题)
1.已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.
(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;
(2)直接写出AM+AN与BM+BN的大小关系.
答案:(1)见解析;(2)AM+AN=BM+BN
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:(1)如图所示.
画法:
①作点M关于射线OP的对称点M',
②连接M'N交OP于点A.
③作点N关于射线OQ的对称点N',
④连接N'M交OQ于点B.
(2)答:AM+AN与BM+BN的大小关系是:AM+AN=BM+BN.
分析:(1)分别作出点M关于射线OP的对称点M',点N关于射线OQ的对称点N',连接M'N、N'M即可求出答案;
(2)根据轴对称性质求出即可.
2.某大型农场拟在公路L旁修建一个农产品储藏、加工厂,将该农场两个规模相同的水果生产基地A、B的水果集中进行储藏和技术加工,以提高经济效益.请你在图中标明加工厂所在的位置C,使A、B两地到加工厂C的运输路程之和最短.(要求:用尺规作图,保留作图痕迹,不写作法和证明)
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:如图
分析:作A关于直线L的对称点E,连接BE交直线L于C,则C为所求.
3.如图,△ABC的边AB、AC上分别有定点M、N,请在BC边上找一点P,使得△PMN的周长最短. (写出作法,保留作图痕迹)
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:①作点N关于BC的对称点N′,连接MN′交BC于点P,
②由对称的性质可知PN=PN′,故PN+PM=MN′,
③由两点之间线段最短可知,△PMN的最短周长即为MN′+MN.
分析:作点N关于BC的对称点N′,连接MN′交BC于点P,由两点之间线段最短可知P点即为所求点.
4.在某一地方,有条小河和草地,一天某牧民的计划是从A处的牧场牵着一只马到草地牧马,再到小河饮马,你能为他设计一条最短的路线吗?(在N上任意一点即可牧马,M上任意一点即可饮马.)(保留作图痕迹,需要证明)
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:沿AC-CD-DB路线走是最短的路线如图(1)所示:
证明:在ON上任意取一点T,在OM上任意取一点R,连接FR、BR、RT、ET、AT,
∵A、E关于ON对称,
∴AC=EC,
同理BD=FD,FR=BR,AT=ET,
∴AC+CD+DB=EC+CD+FD=EF,
AT+TR+BR=ET+TR+FR,
∵ET+TR+FR>EF,
∴AC+CD+DB<AT+TR+BR,
即沿AC-CD-DB路线走是最短的路线.
分析:作A关于ON的对称点E,B关于OM的对称点F,连接EF交ON于C,交OM于D,连接AC、BD,即可得出答案;
根据对称点推出AC=EC,BD=FD,FR=BR,AT=ET,根据两点之间线段最短即可求出答案.
5.已知:如图所示,
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.
答案:见解析
知识点:轴对称-最短路线问题;关于x轴、y轴对称的点的坐标;作图-轴对称变换
解析:
解答:(1)
分别作A、B、C的对称点,A′、B′、C′,由三点的位置可知:
A′(-1,2),B′(-3,1),C′(-4,3)
(2)先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,
(或找出A点关于x轴对称的点A″(1,-2),连接A″C交x轴于点P)则P点即为所求点.
分析:(1)根据轴对称的性质分别作出A、B、C三点关于y轴的对称点A′、B′、C′,分别连接各点即可;
(2)先找出C先找出C点关于x轴对称的点C″(4,-3),连接C″A交x轴于点P,则点p即为所求点.
6.作图题:(写出作法,保留作图痕迹)
M、N为△ABC为AB、AC上的两个定点,请你在BC边上找一点P,使PMN周长最小?
答案:见解析
知识点:轴对称-最短路线问题;作图-轴对称变换
解析:
解答:作法:(1)作M关于BC的对称点M’
(2)连接M’N交BC于P点
(3)连线MP,则△PMN周长最小 P为所求作的点.
分析:由于△PMN的周长=PM+PN+MN,而MN是定值,故只需在BC上找一点P,使PM+PN最小.如果设M关于BC的对称点为M,使PM,+PN最小.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
