新人教版数学八年级下册第十七章勾股定理17.1《勾股定理》课时练习.doc
文档属性
| 名称 | 新人教版数学八年级下册第十七章勾股定理17.1《勾股定理》课时练习.doc |  | |
| 格式 | doc | ||
| 文件大小 | 475.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 08:57:31 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新人教版数学八年级下册第十七章第一节勾股定理课时练习
一、单选题(共15小题)
1.如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
A. 25 B. 12.5 C. 9 D. 8.5
答案:B
知识点:勾股定理 三角形的面积
解析:
解答:四边形ABCD的面积=三角形ACD的面积+三角形ABC的面积=×AC×2+×AC×3=×AC×5=×5×5=12.5,故选B.
分析:正确应用三角形面积公式结合勾股定理求解不规则四边形面积,注意应用面积的割补法.
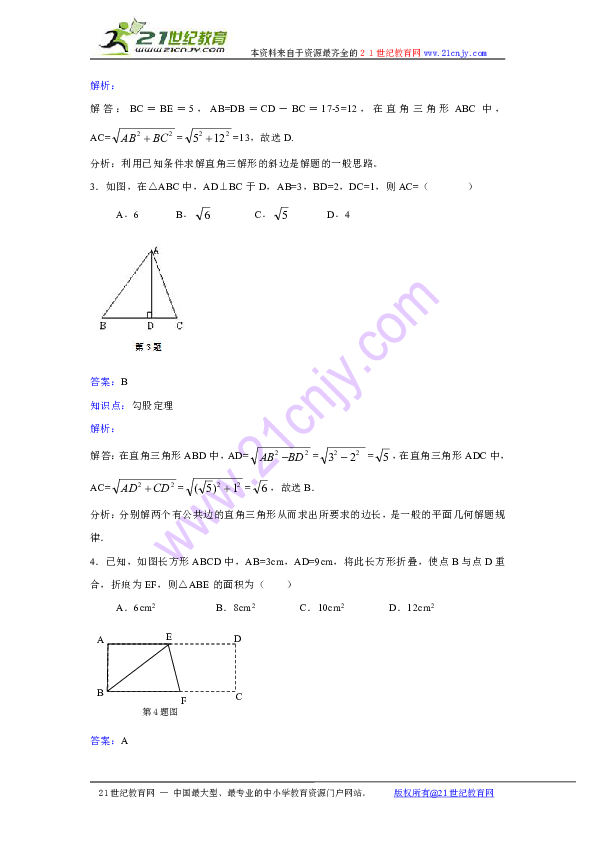
2.如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为( ).
A.12 B.7 C.5 D.13
答案:D
知识点:勾股定理的应用
解析:
解答:BC=BE=5,AB=DB=CD-BC=17-5=12,在直角三角形ABC中,AC===13,故选D.
分析:利用已知条件求解直角三解形的斜边是解题的一般思路。
3.如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,则AC=( )
A.6 B. C. D.4
答案:B
知识点:勾股定理
解析:
解答:在直角三角形ABD中,AD===,在直角三角形ADC中,AC===,故选B.
分析:分别解两个有公共边的直角三角形从而求出所要求的边长,是一般的平面几何解题规律.
4.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
答案:A
知识点:勾股定理
解析:
解答:由直角三角形ABE,得AB+AE=(9-AE),解得AE=4,所以直角三角形ABE的面积=×AB×AE=×3×4=6,故选A.
分析:利用折叠关系和勾股定理列出关于AE的方程是解此题的关键.
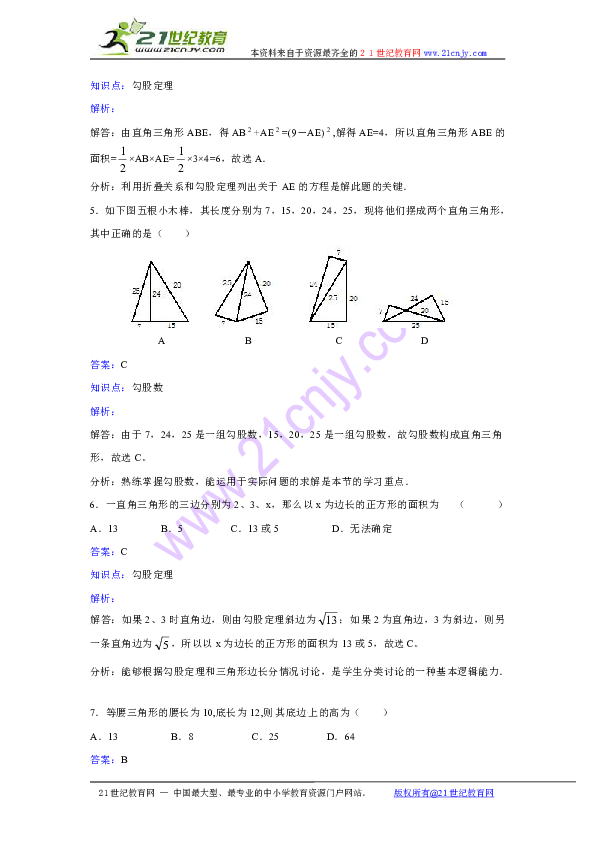
5.如下图五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
A B C D
答案:C
知识点:勾股数
解析:
解答:由于7,24,25是一组勾股数,15,20,25是一组勾股数,故勾股数构成直角三角形,故选C。
分析:熟练掌握勾股数,能运用于实际问题的求解是本节的学习重点.
6.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为 ( )
A.13 B.5 C.13或5 D.无法确定
答案:C
知识点:勾股定理
解析:
解答:如果2、3时直角边,则由勾股定理斜边为;如果2为直角边,3为斜边,则另一条直角边为,所以以x为边长的正方形的面积为13或5,故选C。
分析:能够根据勾股定理和三角形边长分情况讨论,是学生分类讨论的一种基本逻辑能力.
7.等腰三角形的腰长为10,底长为12,则其底边上的高为( )
A.13 B.8 C.25 D.64
答案:B
知识点:勾股定理 等腰三角形的性质
解析:
解答:由题意等腰三角形的腰长为10,底长为12,故底边的一半为6,底边上的高为=8,故选B.
分析:明确等腰三角形底边上的高将等腰三角形分为两个全等的直角三角形,是解此一类型题目的关键.
8. 已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
答案:D
知识点:勾股定理
解析:
解答:若3和4是此直角三角形的两条直角边,此斜边为5;若3为一条直角边,4为斜边,则第三边为,所以第三边长的平方是,故选D.
分析:根据已知条件分情况讨论,是培养学生逻辑思维能力的一个好方法.
9. 直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( )
A.4 cm B.8 cm C.10 cm D.12 cm
答案:C
知识点:勾股定理
解析:
解答:设斜边为x,则由勾股定理得6+(x-2)=x,解之得x=10,故选C.
分析:熟练利用勾股定理列出方程是本节的学习重点之一.
10.如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2﹣13的立方根是( )
A.﹣13 B.﹣﹣13 C.2 D.﹣2
答案:D
知识点:勾股定理
解析:
解答:x=A′B+OB=2+1=5,所以x-13=5-13=-8,-8的立方根为-2,故选D.
分析:根据题目图示正确应用勾股定理进行计算,并能正确求解某实数的立方根是解此题的基本方法.
11.如图,正方形OABC的边长为1,以A为圆心,AC为半径画弧,与数轴的一个交点是D,则D点表示的数为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A. B.
C. D.
答案:A
知识点:二次根式的加减法;勾股定理
解析:
解答:由勾股定理DA=1+1=2,所以DA=,DA=x-x,x=x-DA=1-,故选B.
分析:由数轴正方向求得DA的大小,由线段终点坐标减始点坐标等于线段有方向的数量,求得D点的数轴上的表示的数值大小.
12.已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A.(3,3) B.(3,2)
C.(2,3) D.(3,3)
答案:D
知识点:勾股定理 点的坐标
解析:
解答:由等边三角形三线合一,得C点的横坐标为×6=3,由勾股定理得C点的纵坐标为=3 ,故选D.
分析:利用数形结合的思想,用几何的一些数量关系表达平面直角坐标系当中的点的坐标是一个基本数形应用.
13. 如图是我校的长方形水泥操场,如果一学生要A角走到C角,至少走( )
A.140米 B.120米 C.100米 D.90米
答案:C
知识点:勾股定理
解析:
解答:长方形对角线把长方形分成两个全等的直角三角形,两直角边分别为60米和80米,故斜边AC==100(米),故选C.
分析:根据题意找出直角三角形并用勾股定理正确求解,是用勾股定理求解特殊四边形的常用方法.
14.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.47 D.94
答案:C
知识点:勾股定理的应用
解析:
解答:由勾股定理知E的面积=A的面积+B的面积+C的面积+D的面积=3+5+2+3=47,故选C.
分析:活学活用勾股定理,判断面积之间的数量关系是解此题的关键.
15.如图,长方体的长为15,宽为10,高为20,点离点的距离为5,一只蚂蚁如
果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( )
A. B.25 C. D.
答案:B
知识点:勾股定理;平面展开-最短路径问题
解析:
解答:把长方体侧面展开,A到B的最短距离即线段AB的距离,线段AB恰是以15、20为直角边的直角三角形斜边的长,所以AB=25,即得B.
分析:巧妙应用长方体的侧面展开图,利用直角三角形勾股定理求最短距离是初中学生对于立体几何部分的初步认识,起到了一个启蒙的作用.
二、填空题
1.某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米
答案:7
知识点:勾股定理的应用
解析:
解答:楼梯的宽为=4,地毯的长度为3+4=7米.
分析:正确的将勾股定理运用于实际问题的求解,是学习数学的必要途径.
2、在直角三角形中,斜边=2,则=______
答案:8
知识点:勾股定理
解析:
解答:由题意AB=4,AC+BC=AB,所以AB+AC+BC=8
分析:运用勾股定理求出等量关系是解此题的一般思路.
3、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行___________千米
答案:540
知识点:勾股定理
解析:
解答:由题意,男孩飞行的距离为=3000,故飞行速度为3000÷20=150米/秒=540千米/小时.
分析:将勾股定理运用于实际问题当中,注意单位的细节变化,是考察学生实际应用和细致性的常用方法.
4.在边长为1cm的正△ABC中,P0为BC边上一点,作P0P1⊥CA于点 P1,作P1P2⊥AB于点P2,作P2P3⊥BC于点P3.如果点P3恰与点P0重合,则△P1P2P3的面积是 cm2.
答案:
知识点:勾股定理 等边三角形的性质
解析:
解答:由题意知△P1P2P3每个内角均为180 -90 -30 =60 ,所以△P1P2P3是等边三角形,其顶点分原三角形每个边长为2:1,故△P1P2P3的边长为=,所以其面积为×()=.
分析:能够根据题目求出△P1P2P3每个内角的度数,从而判定△P1P2P3是一个等边三角形,并运用等边三角形面积与边长的关系求出三角形的面积.
5.如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是 ;CE和CG的大小关系 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
答案:a, CE知识点:勾股定理
解析:
解答:补全左上侧小正方形,则阴影部分的面积=(2a+a)×2a-a×a-×2a×2a-×a×(a+2a)=a,CE=(2a)+(2a)=8a,CG=a+(a+2a)=10a,所以CE分析:利用割补法求面积,并能运用勾股定理比较边长的大小.
三、解答题(共5小题)
1.小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知,求的长.
答案:
知识点:勾股定理
解析:
解答:BC=BD+CD=2CD=8,设AC=x,则AB=x,由勾股定理得()+8=x,解之得x=
分析:运用勾股定理求解三角板的边长是典型的特殊直角三角形的应用,学生应牢固掌握.
2.在△ABC中,AB=AC,D是BC延长线上的点,求证:.
答案:证明过点A作AE⊥BD于E,易得
在Rt△AED, Rt△ABE,中由勾股定理
即
知识点:勾股定理的证明
解析:
解答:证明过点A作AE⊥BD于E,易得
在Rt△AED, Rt△ABE,中由勾股定理
即.
分析:充分利用勾股定理进行有关边长平方的等量关系证明是要求学生提高抽象思维能力的一个基本要求,学生应能根据题意合理设计相关三角形进行有效证明
3.一个零件的形状如图所示,已知AC=3,AB=4,BD=12求CD的长.
答案:13cm
知识点:勾股定理
解析:
解答:在直角三角形ABC中,BC===5,在直角三角形BCD中,CD===13
分析:运用勾股定理两次求解直角三角形的斜边长是本题的一个解题关键。
4.已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
答案:∵a,b是Rt△ABC的两条直角边,c是斜边,
∴a2+b2=c2,
即a2=c2﹣b2=(c+b)(c﹣b),
∵a为质数,
∴c+b=a2,c﹣b=1,
∴a2=2b+1,
∴2(a+b+1)=a2+2a+1=(a+1)2,
∴2(a+b+1)是完全平方数.
知识点:勾股定理
解析:
解答∵a,b是Rt△ABC的两条直角边,c是斜边,
∴a2+b2=c2,
即a2=c2﹣b2=(c+b)(c﹣b),
∵a为质数,
∴c+b=a2,c﹣b=1,
∴a2=2b+1,
∴2(a+b+1)=a2+2a+1=(a+1)2,
∴2(a+b+1)是完全平方数.分析:根据题意和折扣关系列出方程并正确求解,是解此类型题目的基本方法.
分析:此题考查完全平方数,根据勾股定理和a为质数展开答题,是关键
5.一个直角三角形的边长都是整数,它的面积和周长的数值相等.试确定这个直角三角形三边的长.
答案:设直角边为a,b 由题意得:
=++
移项,平方并化简得到:
+2﹣(+)=0
∵≠0
∴+﹣=2
===4+
∵b是正整数
∴①a=5,b=12,c=13
②a=6,b=8,c=10
③a=8,b=6,c=10
④a=12,b=5,c=13
∴符合题意的直角三角形的斜边长10或13.
知识点:勾股定理;分式方程的解
解析:
解答:设直角边为a,b 由题意得:
=a+b+
移项,平方并化简得到:
+2ab﹣ab(a+b)=0
∵ab≠0
∴a+b﹣=2
b===4+
∵b是正整数
∴①a=5,b=12,c=13
②a=6,b=8,c=10
③a=8,b=6,c=10
④a=12,b=5,c=13
∴符合题意的直角三角形的斜边长10或13.
分析:此题主要考查了勾股定理与求方程的整数解的综合运用,用到了数学中的分类讨论思想,注注意讨论是要考虑全面.
A
B
E
D
C
A
B
E
F
D
C
第4题图
5
20
15
10
C
A
B
第3题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新人教版数学八年级下册第十七章第一节勾股定理课时练习
一、单选题(共15小题)
1.如图小方格都是边长为1的正方形,则四边形ABCD的面积是 ( )
A. 25 B. 12.5 C. 9 D. 8.5
答案:B
知识点:勾股定理 三角形的面积
解析:
解答:四边形ABCD的面积=三角形ACD的面积+三角形ABC的面积=×AC×2+×AC×3=×AC×5=×5×5=12.5,故选B.
分析:正确应用三角形面积公式结合勾股定理求解不规则四边形面积,注意应用面积的割补法.
2.如图,AB⊥CD于B,△ABD和△BCE都是等腰直角三角形,如果CD=17,BE=5,那么AC的长为( ).
A.12 B.7 C.5 D.13
答案:D
知识点:勾股定理的应用
解析:
解答:BC=BE=5,AB=DB=CD-BC=17-5=12,在直角三角形ABC中,AC===13,故选D.
分析:利用已知条件求解直角三解形的斜边是解题的一般思路。
3.如图,在△ABC中,AD⊥BC于D,AB=3,BD=2,DC=1,则AC=( )
A.6 B. C. D.4
答案:B
知识点:勾股定理
解析:
解答:在直角三角形ABD中,AD===,在直角三角形ADC中,AC===,故选B.
分析:分别解两个有公共边的直角三角形从而求出所要求的边长,是一般的平面几何解题规律.
4.已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A.6cm2 B.8cm2 C.10cm2 D.12cm2
答案:A
知识点:勾股定理
解析:
解答:由直角三角形ABE,得AB+AE=(9-AE),解得AE=4,所以直角三角形ABE的面积=×AB×AE=×3×4=6,故选A.
分析:利用折叠关系和勾股定理列出关于AE的方程是解此题的关键.
5.如下图五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( )
A B C D
答案:C
知识点:勾股数
解析:
解答:由于7,24,25是一组勾股数,15,20,25是一组勾股数,故勾股数构成直角三角形,故选C。
分析:熟练掌握勾股数,能运用于实际问题的求解是本节的学习重点.
6.一直角三角形的三边分别为2、3、x,那么以x为边长的正方形的面积为 ( )
A.13 B.5 C.13或5 D.无法确定
答案:C
知识点:勾股定理
解析:
解答:如果2、3时直角边,则由勾股定理斜边为;如果2为直角边,3为斜边,则另一条直角边为,所以以x为边长的正方形的面积为13或5,故选C。
分析:能够根据勾股定理和三角形边长分情况讨论,是学生分类讨论的一种基本逻辑能力.
7.等腰三角形的腰长为10,底长为12,则其底边上的高为( )
A.13 B.8 C.25 D.64
答案:B
知识点:勾股定理 等腰三角形的性质
解析:
解答:由题意等腰三角形的腰长为10,底长为12,故底边的一半为6,底边上的高为=8,故选B.
分析:明确等腰三角形底边上的高将等腰三角形分为两个全等的直角三角形,是解此一类型题目的关键.
8. 已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
答案:D
知识点:勾股定理
解析:
解答:若3和4是此直角三角形的两条直角边,此斜边为5;若3为一条直角边,4为斜边,则第三边为,所以第三边长的平方是,故选D.
分析:根据已知条件分情况讨论,是培养学生逻辑思维能力的一个好方法.
9. 直角三角形的斜边比一直角边长2 cm,另一直角边长为6 cm,则它的斜边长( )
A.4 cm B.8 cm C.10 cm D.12 cm
答案:C
知识点:勾股定理
解析:
解答:设斜边为x,则由勾股定理得6+(x-2)=x,解之得x=10,故选C.
分析:熟练利用勾股定理列出方程是本节的学习重点之一.
10.如图,已知矩形A′BOC的边长A′B=2,OB=1,数轴上点A表示的数为x,则x2﹣13的立方根是( )
A.﹣13 B.﹣﹣13 C.2 D.﹣2
答案:D
知识点:勾股定理
解析:
解答:x=A′B+OB=2+1=5,所以x-13=5-13=-8,-8的立方根为-2,故选D.
分析:根据题目图示正确应用勾股定理进行计算,并能正确求解某实数的立方根是解此题的基本方法.
11.如图,正方形OABC的边长为1,以A为圆心,AC为半径画弧,与数轴的一个交点是D,则D点表示的数为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A. B.
C. D.
答案:A
知识点:二次根式的加减法;勾股定理
解析:
解答:由勾股定理DA=1+1=2,所以DA=,DA=x-x,x=x-DA=1-,故选B.
分析:由数轴正方向求得DA的大小,由线段终点坐标减始点坐标等于线段有方向的数量,求得D点的数轴上的表示的数值大小.
12.已知等边△ABC,点A在坐标原点,B点的坐标为(6,0),则点C的坐标为( )
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
A.(3,3) B.(3,2)
C.(2,3) D.(3,3)
答案:D
知识点:勾股定理 点的坐标
解析:
解答:由等边三角形三线合一,得C点的横坐标为×6=3,由勾股定理得C点的纵坐标为=3 ,故选D.
分析:利用数形结合的思想,用几何的一些数量关系表达平面直角坐标系当中的点的坐标是一个基本数形应用.
13. 如图是我校的长方形水泥操场,如果一学生要A角走到C角,至少走( )
A.140米 B.120米 C.100米 D.90米
答案:C
知识点:勾股定理
解析:
解答:长方形对角线把长方形分成两个全等的直角三角形,两直角边分别为60米和80米,故斜边AC==100(米),故选C.
分析:根据题意找出直角三角形并用勾股定理正确求解,是用勾股定理求解特殊四边形的常用方法.
14.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
A.13 B.26 C.47 D.94
答案:C
知识点:勾股定理的应用
解析:
解答:由勾股定理知E的面积=A的面积+B的面积+C的面积+D的面积=3+5+2+3=47,故选C.
分析:活学活用勾股定理,判断面积之间的数量关系是解此题的关键.
15.如图,长方体的长为15,宽为10,高为20,点离点的距离为5,一只蚂蚁如
果要沿着长方体的表面从点爬到点,需要爬行的最短距离是( )
A. B.25 C. D.
答案:B
知识点:勾股定理;平面展开-最短路径问题
解析:
解答:把长方体侧面展开,A到B的最短距离即线段AB的距离,线段AB恰是以15、20为直角边的直角三角形斜边的长,所以AB=25,即得B.
分析:巧妙应用长方体的侧面展开图,利用直角三角形勾股定理求最短距离是初中学生对于立体几何部分的初步认识,起到了一个启蒙的作用.
二、填空题
1.某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要____________米
答案:7
知识点:勾股定理的应用
解析:
解答:楼梯的宽为=4,地毯的长度为3+4=7米.
分析:正确的将勾股定理运用于实际问题的求解,是学习数学的必要途径.
2、在直角三角形中,斜边=2,则=______
答案:8
知识点:勾股定理
解析:
解答:由题意AB=4,AC+BC=AB,所以AB+AC+BC=8
分析:运用勾股定理求出等量关系是解此题的一般思路.
3、飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶正上方4000米处,过了20秒,飞机距离这个男孩头顶5000米,求飞机每小时飞行___________千米
答案:540
知识点:勾股定理
解析:
解答:由题意,男孩飞行的距离为=3000,故飞行速度为3000÷20=150米/秒=540千米/小时.
分析:将勾股定理运用于实际问题当中,注意单位的细节变化,是考察学生实际应用和细致性的常用方法.
4.在边长为1cm的正△ABC中,P0为BC边上一点,作P0P1⊥CA于点 P1,作P1P2⊥AB于点P2,作P2P3⊥BC于点P3.如果点P3恰与点P0重合,则△P1P2P3的面积是 cm2.
答案:
知识点:勾股定理 等边三角形的性质
解析:
解答:由题意知△P1P2P3每个内角均为180 -90 -30 =60 ,所以△P1P2P3是等边三角形,其顶点分原三角形每个边长为2:1,故△P1P2P3的边长为=,所以其面积为×()=.
分析:能够根据题目求出△P1P2P3每个内角的度数,从而判定△P1P2P3是一个等边三角形,并运用等边三角形面积与边长的关系求出三角形的面积.
5.如图,正方形BCDE和ABFG的边长分别为2a,a,连接CE和CG,则图中阴影部分的面积是 ;CE和CG的大小关系 .
( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
答案:a, CE
解析:
解答:补全左上侧小正方形,则阴影部分的面积=(2a+a)×2a-a×a-×2a×2a-×a×(a+2a)=a,CE=(2a)+(2a)=8a,CG=a+(a+2a)=10a,所以CE
三、解答题(共5小题)
1.小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知,求的长.
答案:
知识点:勾股定理
解析:
解答:BC=BD+CD=2CD=8,设AC=x,则AB=x,由勾股定理得()+8=x,解之得x=
分析:运用勾股定理求解三角板的边长是典型的特殊直角三角形的应用,学生应牢固掌握.
2.在△ABC中,AB=AC,D是BC延长线上的点,求证:.
答案:证明过点A作AE⊥BD于E,易得
在Rt△AED, Rt△ABE,中由勾股定理
即
知识点:勾股定理的证明
解析:
解答:证明过点A作AE⊥BD于E,易得
在Rt△AED, Rt△ABE,中由勾股定理
即.
分析:充分利用勾股定理进行有关边长平方的等量关系证明是要求学生提高抽象思维能力的一个基本要求,学生应能根据题意合理设计相关三角形进行有效证明
3.一个零件的形状如图所示,已知AC=3,AB=4,BD=12求CD的长.
答案:13cm
知识点:勾股定理
解析:
解答:在直角三角形ABC中,BC===5,在直角三角形BCD中,CD===13
分析:运用勾股定理两次求解直角三角形的斜边长是本题的一个解题关键。
4.已知Rt△ABC的两条直角边的长a、b均为整数,且a为质数,若斜边c也是整数,求证:2(a+b+1)是完全平方数.
答案:∵a,b是Rt△ABC的两条直角边,c是斜边,
∴a2+b2=c2,
即a2=c2﹣b2=(c+b)(c﹣b),
∵a为质数,
∴c+b=a2,c﹣b=1,
∴a2=2b+1,
∴2(a+b+1)=a2+2a+1=(a+1)2,
∴2(a+b+1)是完全平方数.
知识点:勾股定理
解析:
解答∵a,b是Rt△ABC的两条直角边,c是斜边,
∴a2+b2=c2,
即a2=c2﹣b2=(c+b)(c﹣b),
∵a为质数,
∴c+b=a2,c﹣b=1,
∴a2=2b+1,
∴2(a+b+1)=a2+2a+1=(a+1)2,
∴2(a+b+1)是完全平方数.分析:根据题意和折扣关系列出方程并正确求解,是解此类型题目的基本方法.
分析:此题考查完全平方数,根据勾股定理和a为质数展开答题,是关键
5.一个直角三角形的边长都是整数,它的面积和周长的数值相等.试确定这个直角三角形三边的长.
答案:设直角边为a,b 由题意得:
=++
移项,平方并化简得到:
+2﹣(+)=0
∵≠0
∴+﹣=2
===4+
∵b是正整数
∴①a=5,b=12,c=13
②a=6,b=8,c=10
③a=8,b=6,c=10
④a=12,b=5,c=13
∴符合题意的直角三角形的斜边长10或13.
知识点:勾股定理;分式方程的解
解析:
解答:设直角边为a,b 由题意得:
=a+b+
移项,平方并化简得到:
+2ab﹣ab(a+b)=0
∵ab≠0
∴a+b﹣=2
b===4+
∵b是正整数
∴①a=5,b=12,c=13
②a=6,b=8,c=10
③a=8,b=6,c=10
④a=12,b=5,c=13
∴符合题意的直角三角形的斜边长10或13.
分析:此题主要考查了勾股定理与求方程的整数解的综合运用,用到了数学中的分类讨论思想,注注意讨论是要考虑全面.
A
B
E
D
C
A
B
E
F
D
C
第4题图
5
20
15
10
C
A
B
第3题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
