重庆市巴渝学校2023-2024学年九年级下学期开学考试数学试题(pdf版无答案)
文档属性
| 名称 | 重庆市巴渝学校2023-2024学年九年级下学期开学考试数学试题(pdf版无答案) | 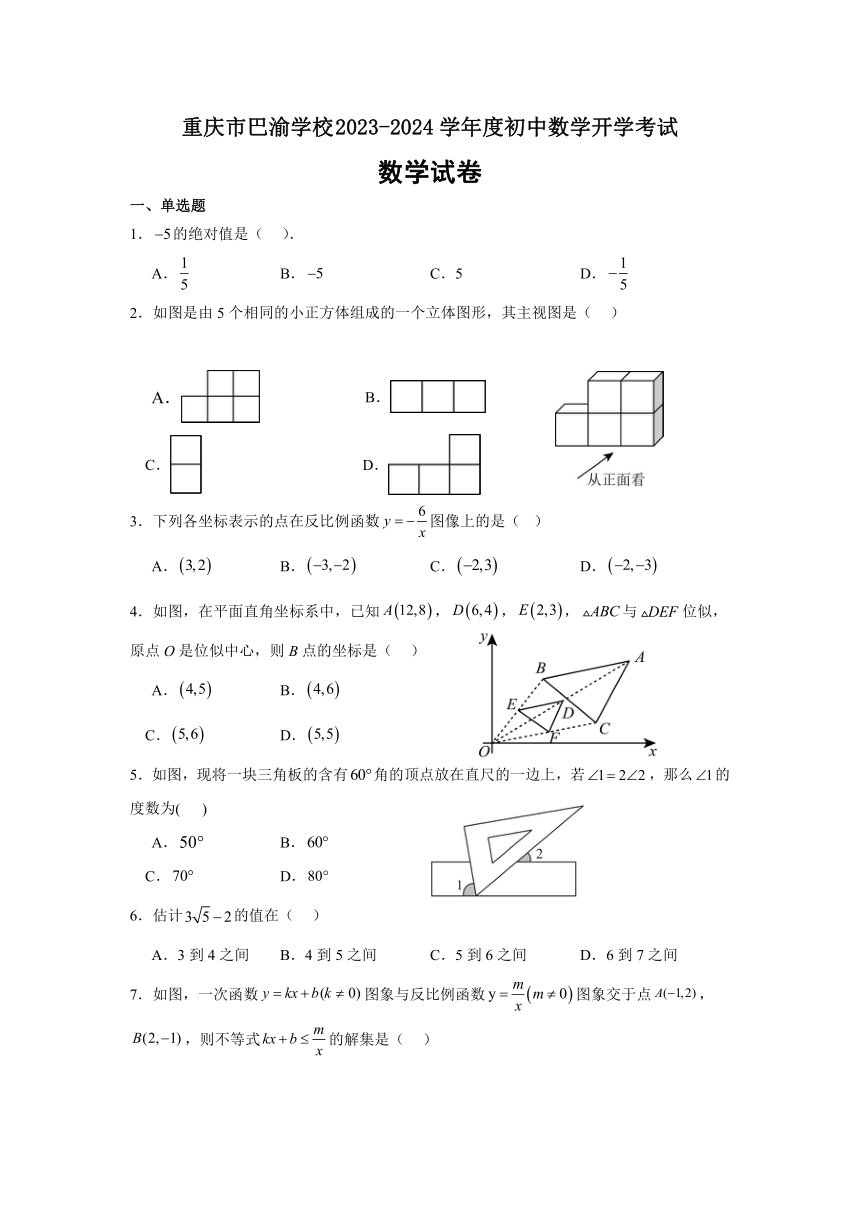 | |
| 格式 | |||
| 文件大小 | 498.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 12:38:24 | ||
图片预览




文档简介
重庆市巴渝学校2023-2024 学年度初中数学开学考试
数学试卷
一、单选题
1. 5的绝对值是( ).
1 1
A. B. 5 C.5 D.
5 5
2.如图是由 5个相同的小正方体组成的一个立体图形,其主视图是( )
A. B.
C. D.
6
3.下列各坐标表示的点在反比例函数 y 图像上的是( )
x
A. 3,2 B. 3, 2 C. 2,3 D. 2, 3
4.如图,在平面直角坐标系中,已知 A 12,8 ,D 6,4 , E 2,3 , ABC与 DEF位似,
原点 O是位似中心,则 B点的坐标是( )
A. 4,5 B. 4,6
C. 5,6 D. 5,5
5.如图,现将一块三角板的含有60 角的顶点放在直尺的一边上,若 1 2 2,那么 1的
度数为( )
A.50 B.60
C.70 D.80
6.估计3 5 2的值在( )
A.3到 4之间 B.4到 5之间 C.5到 6之间 D.6到 7之间
m
7.如图,一次函数 y kx b(k 0)图象与反比例函数 y m 0 图象交于点 A( 1,2),
x
B(2, 1) kx b m,则不等式 的解集是( )
x
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
A. x 1或 x 2 B. 1 x 0或0 x 2
C. x 1或0 x 2 D. 1 x 0或 x 2
8.如图,已知 AB是 O的直径,CD是弦,若 BCD 36 ,则 DAB等于( )
A.54 B.56
C.64 D.36
9.如图,点 E为正方形 ABCD内一点, AD ED, AED 70 ,连结 EC,那么 AEC的
度数是( )
A.105 B.130
C.135 D.140
10.己知 x y z m n,从 y、z、m、n中随机取两个字母作差,记为 A;将剩下两个字
母作差后取绝对值,记为 B;再对 x A B 进行化简运算,称此为“和差操作”,例如:
x z n m y x z n m y x y z m n为一次“和差操作”, x y z m n为
“和差操作”的一种运算结果下列说法:
①存在两种“和差操作”运算结果的和为 2x;
②不存在两种“和差操作”运算结果的差为 2m 2n;
③所有的“和差操作”共有 5种不同运算结果.
其中正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题
11 0.计算: 2021 4 .
12.若一个正多边形的每一个外角都是 30°,则这个正多边形的内角和等于 度.
13.有四张大小和背面完全相同的不透明卡片,正面分别印有“1”、“2”、“3”、“6”四个数字,
将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上数字的积为 6
的概率是 .
14.某种商品原来每件售价为 200元,经过连续两次降价后,该种商品每件售价为 128元,
设平均每次降价的百分率为 x,根据题意,可列方程为 .
答案第 2页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
15.如图,在 ABC中, ACB 60 , BAC 75 ,AD BC于 D,BE AC于 E,AD
与BE交于 H,则 CHD .
16.如图,半圆O的直径 AB 2, P为 AB上一点,点C,D为半圆的三等分点,则阴影部
分的面积为 .
3y 1 1 y
17 y 2 2
x 4a 1
.若关于 的不等式组 1 无解,且关于
x的分式方程 1的解为
y a 0
x 1 x 1
5
负数,则所有满足条件的整数 a的值之和是 .
18.一个两位正整数,将其个位与十位上的数交换位置后,放在原数的后面组成一个四位数
m,那么我们把这个四位数称为“顺利数”,并规定 F m 为交换位置后组成的两位数与原两
位数的平方差;例如:将 27交换位置后为 72,则 2772是一个“顺利数”,且
F 2772 72 2 27 2 4455 .若四位正整数 n,n的千位数字为 a,百位数字为 b,十位数字
为 c,个位数字为 d,其中 a,b,c,d为整数,1 a,b,c,d 9 ,且 c d,以 n的十位数
字和个位数字组成两位数,交换位置后放在此两位数之后组成的数为“顺利数”s,若
F s 1001a 110b,则 a b的值为 ;满足条件的所有数 n的最大值为 .
三、解答题
19.计算:
5 m 3
(1) m 2
; (2) (x y)
2 x x y .
m 2 2m 4
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
20.小南在学习过程中遇到了一个问题:试说明顶角为 120°的等腰三角形的面积,与以其
腰为边长的等边三角形的面积相等,已知:在△ABC中, AB AC, BAC 120 ,她
的思路是以 AC为边构造等边三角形△ACE,将问题转化为证明三角形全等,根据全等三
角形的面积相等使问题得到解决,请根据小南的思路完成下面的作图与填空:
证明:用直尺和圆规,在 BC 下方作 BCD ABC ,在射线 CD 上截取一点 E,使得
CE CA,连接 AE交 BC于点 F(只保留作图痕迹).
在△ABC中,____①__________,且 BAC 120 ,
ABC ACB 60 ,
BCD ABC,
ACE BCD ACB 60 ,
CE CA,
∴____②_____________,
AB AC,CE CA,
AB EC,
在△ABF 和△ECF 中,
ABF ECF
____③____
AB EC
△ABF≌△ECF AAS .
∴____④_____________.
S△ABC S△ABF S△ACF , S△ACE S△ECF S△ACF ,
S△ABC S△ACE .
21.我校在七、八年级学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各随机
抽取 10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用 x表示,共分成
四组:A.130 x 135,B.135 x 140,C.140 x 145,D.145 x 150),
下面给出了部分信息:
七年级抽取的 10名学生的竞赛成绩:131,134,135,138,141,147,148,148,148,150.
八年级 10名学生的竞赛成绩在 C组中的数据是 140,143,143,144.
答案第 4页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
七、八年级抽取的学生的竞赛成绩统计表
年级 七年级 八年级
平均数 142 142
中位数 144 b
众数 c 143
根据以上信息,解答下列问题:
(1)填空:a=______,b=______,c=______;
(2)根据以上数据分析,你认为我校七、八年级中哪个年级学生竞赛成绩较好?请说明理
由(一条理由即可);
(3)我校七、八年级分别有 780名、620学生参加了此次竞赛,请估计成绩达到 140分及
以上的学生共有多少名?
22.如图,Rt△ABC中, AB 6, AC 8,动点 M、N分别以每秒 3个单位长度、4个单
位长度的速度同时从 A出发,点 M沿折线 A B C方向运动,点 N沿折线 A C B方
向运动,点 M达点 B后,点 M、点 N的运动速度均变为每秒 1个单位长度运动,当两点相
遇时停止运动,设运动时间为 t秒,点 M、N的距离为 y.
(1)请直接写出 y关于 t的函数表达式并直接写出自变量 t的取值范围;
(2)在给定的平面直角坐标系中画出函数的图像,并写出函数的一条性质;
(3)当 M,N两点相距 6个单位长度时,直接写出 t的值.
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
23.某水果店以相同的进价购进两批樱桃,第一批 80千克,每千克 16元出售;第二批 60
千克,每千克 18元出售,两批樱桃全部售完,店主共获利 960元.
(1)求樱桃的进价是每千克多少元?
(2)该水果店一相同的进价购进第三批樱桃若干,第一天将樱桃涨价到每千克 20元出售,
结果仅售出 40千克;为了尽快售完第三批樱桃,第二天店主决定在第一天售价的基础上降
价促销,若在第一天售价基础上每降价 1元,第二天的销售量就在第一天的基础上增加 10
千克.到第二天晚上关店时樱桃售完,店主销售第三批樱桃获得的利润为 850元,求第二天
樱桃的售价是每千克多少元?
24.五一假期,不少人选择乘坐飞机出游.妈妈和小明从航站楼入口点 B处前往登机口点 A
处登机.已知点 A位于点 B东北方向且 AB 100米.点 B的正东方向有另一入口点C,商
店D位于点C的正北方向,同时位于点 A的南偏东 60 , AD 40米.
(1)求两个入口 BC的距离;(结果保留根号)
(2)妈妈和小明到达航站楼时间为上午 9 : 00,登机时间为 9 :30.妈妈见时间尚早,决定
和小明一起先去商店D处逛逛,他们沿 B C D A路线行走,步行速度为 60米 /分,
在商店D处逗留 25分钟,请计算说明妈妈和小明是否能准时登机?(参考数据: 2 1.41,
3 1.73)
答案第 6页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
1
25. 1 y ax
2 bx c a 0 y x 2如图 ,在平面直角坐标系中,抛物线 与直线 2 交于 x轴
3
上的点 B, y
x
轴上的点C,且其对称轴为直线 2 .该抛物线与 x轴的另一交点为点 A,
顶点为M .
(1)求抛物线的解析式及顶点M 的坐标;
(2)如图 2,长度为 5 的线段DF 在线段 BC上滑动(点 D在点 F 的左侧),过D, F 分
别作 y轴的平行线,交抛物线于 E, P两点,连接 PE ,求四边形 PFDE面积的最大值及此
时点 P坐标;
(3)在(2)问条件下,当四边形 PFDE 面积有最大值时,记四边形 PFDE 为四边形
P1F1D1E1.将四边形 P1F1D1E1 沿直线 BC平移,点 P1,E1关于直线 BC的对称点分别是点 P2,
E2 .在平移过程中,当点 P2,E2 中有一点落到抛物线上时,请直接写出点 P2,E2 的坐标.
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
26.已知 ABC是等边三角形,
(1)如图 1,若 AB 4,点 D在线段BC上,且 BD 1,连接 AD,求 AD的长;
(2)如图 2,点 E是BC延长线上一点, AEF 60 ,EF 交 ABC的外角平分线于点 F,求证:
CF AC CE;
(3)如图 3,若 AB 8,动点 M从点 B出发,沿射线 BC方向移动,以 AM 为边在右侧作等
边 AMN ,取 AC中点 H,连接 NH ,请直接写出 NH 的最小值及此时 BM的长.
答案第 8页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
数学试卷
一、单选题
1. 5的绝对值是( ).
1 1
A. B. 5 C.5 D.
5 5
2.如图是由 5个相同的小正方体组成的一个立体图形,其主视图是( )
A. B.
C. D.
6
3.下列各坐标表示的点在反比例函数 y 图像上的是( )
x
A. 3,2 B. 3, 2 C. 2,3 D. 2, 3
4.如图,在平面直角坐标系中,已知 A 12,8 ,D 6,4 , E 2,3 , ABC与 DEF位似,
原点 O是位似中心,则 B点的坐标是( )
A. 4,5 B. 4,6
C. 5,6 D. 5,5
5.如图,现将一块三角板的含有60 角的顶点放在直尺的一边上,若 1 2 2,那么 1的
度数为( )
A.50 B.60
C.70 D.80
6.估计3 5 2的值在( )
A.3到 4之间 B.4到 5之间 C.5到 6之间 D.6到 7之间
m
7.如图,一次函数 y kx b(k 0)图象与反比例函数 y m 0 图象交于点 A( 1,2),
x
B(2, 1) kx b m,则不等式 的解集是( )
x
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
A. x 1或 x 2 B. 1 x 0或0 x 2
C. x 1或0 x 2 D. 1 x 0或 x 2
8.如图,已知 AB是 O的直径,CD是弦,若 BCD 36 ,则 DAB等于( )
A.54 B.56
C.64 D.36
9.如图,点 E为正方形 ABCD内一点, AD ED, AED 70 ,连结 EC,那么 AEC的
度数是( )
A.105 B.130
C.135 D.140
10.己知 x y z m n,从 y、z、m、n中随机取两个字母作差,记为 A;将剩下两个字
母作差后取绝对值,记为 B;再对 x A B 进行化简运算,称此为“和差操作”,例如:
x z n m y x z n m y x y z m n为一次“和差操作”, x y z m n为
“和差操作”的一种运算结果下列说法:
①存在两种“和差操作”运算结果的和为 2x;
②不存在两种“和差操作”运算结果的差为 2m 2n;
③所有的“和差操作”共有 5种不同运算结果.
其中正确的个数是( )
A.0 B.1 C.2 D.3
二、填空题
11 0.计算: 2021 4 .
12.若一个正多边形的每一个外角都是 30°,则这个正多边形的内角和等于 度.
13.有四张大小和背面完全相同的不透明卡片,正面分别印有“1”、“2”、“3”、“6”四个数字,
将这四张卡片背面朝上洗匀,从中随机抽取两张卡片,所抽取的卡片正面上数字的积为 6
的概率是 .
14.某种商品原来每件售价为 200元,经过连续两次降价后,该种商品每件售价为 128元,
设平均每次降价的百分率为 x,根据题意,可列方程为 .
答案第 2页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
15.如图,在 ABC中, ACB 60 , BAC 75 ,AD BC于 D,BE AC于 E,AD
与BE交于 H,则 CHD .
16.如图,半圆O的直径 AB 2, P为 AB上一点,点C,D为半圆的三等分点,则阴影部
分的面积为 .
3y 1 1 y
17 y 2 2
x 4a 1
.若关于 的不等式组 1 无解,且关于
x的分式方程 1的解为
y a 0
x 1 x 1
5
负数,则所有满足条件的整数 a的值之和是 .
18.一个两位正整数,将其个位与十位上的数交换位置后,放在原数的后面组成一个四位数
m,那么我们把这个四位数称为“顺利数”,并规定 F m 为交换位置后组成的两位数与原两
位数的平方差;例如:将 27交换位置后为 72,则 2772是一个“顺利数”,且
F 2772 72 2 27 2 4455 .若四位正整数 n,n的千位数字为 a,百位数字为 b,十位数字
为 c,个位数字为 d,其中 a,b,c,d为整数,1 a,b,c,d 9 ,且 c d,以 n的十位数
字和个位数字组成两位数,交换位置后放在此两位数之后组成的数为“顺利数”s,若
F s 1001a 110b,则 a b的值为 ;满足条件的所有数 n的最大值为 .
三、解答题
19.计算:
5 m 3
(1) m 2
; (2) (x y)
2 x x y .
m 2 2m 4
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
20.小南在学习过程中遇到了一个问题:试说明顶角为 120°的等腰三角形的面积,与以其
腰为边长的等边三角形的面积相等,已知:在△ABC中, AB AC, BAC 120 ,她
的思路是以 AC为边构造等边三角形△ACE,将问题转化为证明三角形全等,根据全等三
角形的面积相等使问题得到解决,请根据小南的思路完成下面的作图与填空:
证明:用直尺和圆规,在 BC 下方作 BCD ABC ,在射线 CD 上截取一点 E,使得
CE CA,连接 AE交 BC于点 F(只保留作图痕迹).
在△ABC中,____①__________,且 BAC 120 ,
ABC ACB 60 ,
BCD ABC,
ACE BCD ACB 60 ,
CE CA,
∴____②_____________,
AB AC,CE CA,
AB EC,
在△ABF 和△ECF 中,
ABF ECF
____③____
AB EC
△ABF≌△ECF AAS .
∴____④_____________.
S△ABC S△ABF S△ACF , S△ACE S△ECF S△ACF ,
S△ABC S△ACE .
21.我校在七、八年级学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各随机
抽取 10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用 x表示,共分成
四组:A.130 x 135,B.135 x 140,C.140 x 145,D.145 x 150),
下面给出了部分信息:
七年级抽取的 10名学生的竞赛成绩:131,134,135,138,141,147,148,148,148,150.
八年级 10名学生的竞赛成绩在 C组中的数据是 140,143,143,144.
答案第 4页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
七、八年级抽取的学生的竞赛成绩统计表
年级 七年级 八年级
平均数 142 142
中位数 144 b
众数 c 143
根据以上信息,解答下列问题:
(1)填空:a=______,b=______,c=______;
(2)根据以上数据分析,你认为我校七、八年级中哪个年级学生竞赛成绩较好?请说明理
由(一条理由即可);
(3)我校七、八年级分别有 780名、620学生参加了此次竞赛,请估计成绩达到 140分及
以上的学生共有多少名?
22.如图,Rt△ABC中, AB 6, AC 8,动点 M、N分别以每秒 3个单位长度、4个单
位长度的速度同时从 A出发,点 M沿折线 A B C方向运动,点 N沿折线 A C B方
向运动,点 M达点 B后,点 M、点 N的运动速度均变为每秒 1个单位长度运动,当两点相
遇时停止运动,设运动时间为 t秒,点 M、N的距离为 y.
(1)请直接写出 y关于 t的函数表达式并直接写出自变量 t的取值范围;
(2)在给定的平面直角坐标系中画出函数的图像,并写出函数的一条性质;
(3)当 M,N两点相距 6个单位长度时,直接写出 t的值.
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
23.某水果店以相同的进价购进两批樱桃,第一批 80千克,每千克 16元出售;第二批 60
千克,每千克 18元出售,两批樱桃全部售完,店主共获利 960元.
(1)求樱桃的进价是每千克多少元?
(2)该水果店一相同的进价购进第三批樱桃若干,第一天将樱桃涨价到每千克 20元出售,
结果仅售出 40千克;为了尽快售完第三批樱桃,第二天店主决定在第一天售价的基础上降
价促销,若在第一天售价基础上每降价 1元,第二天的销售量就在第一天的基础上增加 10
千克.到第二天晚上关店时樱桃售完,店主销售第三批樱桃获得的利润为 850元,求第二天
樱桃的售价是每千克多少元?
24.五一假期,不少人选择乘坐飞机出游.妈妈和小明从航站楼入口点 B处前往登机口点 A
处登机.已知点 A位于点 B东北方向且 AB 100米.点 B的正东方向有另一入口点C,商
店D位于点C的正北方向,同时位于点 A的南偏东 60 , AD 40米.
(1)求两个入口 BC的距离;(结果保留根号)
(2)妈妈和小明到达航站楼时间为上午 9 : 00,登机时间为 9 :30.妈妈见时间尚早,决定
和小明一起先去商店D处逛逛,他们沿 B C D A路线行走,步行速度为 60米 /分,
在商店D处逗留 25分钟,请计算说明妈妈和小明是否能准时登机?(参考数据: 2 1.41,
3 1.73)
答案第 6页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
1
25. 1 y ax
2 bx c a 0 y x 2如图 ,在平面直角坐标系中,抛物线 与直线 2 交于 x轴
3
上的点 B, y
x
轴上的点C,且其对称轴为直线 2 .该抛物线与 x轴的另一交点为点 A,
顶点为M .
(1)求抛物线的解析式及顶点M 的坐标;
(2)如图 2,长度为 5 的线段DF 在线段 BC上滑动(点 D在点 F 的左侧),过D, F 分
别作 y轴的平行线,交抛物线于 E, P两点,连接 PE ,求四边形 PFDE面积的最大值及此
时点 P坐标;
(3)在(2)问条件下,当四边形 PFDE 面积有最大值时,记四边形 PFDE 为四边形
P1F1D1E1.将四边形 P1F1D1E1 沿直线 BC平移,点 P1,E1关于直线 BC的对称点分别是点 P2,
E2 .在平移过程中,当点 P2,E2 中有一点落到抛物线上时,请直接写出点 P2,E2 的坐标.
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
26.已知 ABC是等边三角形,
(1)如图 1,若 AB 4,点 D在线段BC上,且 BD 1,连接 AD,求 AD的长;
(2)如图 2,点 E是BC延长线上一点, AEF 60 ,EF 交 ABC的外角平分线于点 F,求证:
CF AC CE;
(3)如图 3,若 AB 8,动点 M从点 B出发,沿射线 BC方向移动,以 AM 为边在右侧作等
边 AMN ,取 AC中点 H,连接 NH ,请直接写出 NH 的最小值及此时 BM的长.
答案第 8页,共 8页
{#{QQABDYQQogCgABBAAAhCAwXICACQkAAAAKoGABAMMAABCQFABAA=}#}
同课章节目录
