28.1锐角三角函数同步练习(含简单答案)人教版(2012)数学九年级下册
文档属性
| 名称 | 28.1锐角三角函数同步练习(含简单答案)人教版(2012)数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 406.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 14:09:16 | ||
图片预览


文档简介
28.1锐角三角函数同步练习人教版(2012)数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.若∠ACF=2∠ABD,∠BFC=132°,则cosA的值为 ( )
A. B. C. D.
2.角,满足,下列是关于角,的命题,其中错误的是( )
A. B. C. D.
3.计算的值等于( )
A. B.
C. D.
4.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
5.矩形纸片中,E为的中点,连接,将沿折叠得到,连接.若,,则的长是( )
A.3 B. C. D.
6.如图,在中,,,,,则下列选项正确的是( )
A. B. C. D.
7.已知锐角α,且sinα=cos38°,则α=( )
A.38° B.62° C.52° D.72°
8.如图,网格中小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( ).
A. B. C. D.
9.在中,,,则( )
A. B. C. D.
10.如图,已知 两点的坐标分别为,点分别是直线和x轴上的动点,,点是线段的中点,连接交轴于点;当⊿面积取得最小值时,的值是( )
A. B. C. D.
二、填空题
11.在三角形ABC中,AB=4,tanC=1,那么BC+AC的最大值为 .
12.如图,△ABC内接于圆O,若圆的半径是2.5,AB=3,则∠C的正切值= .
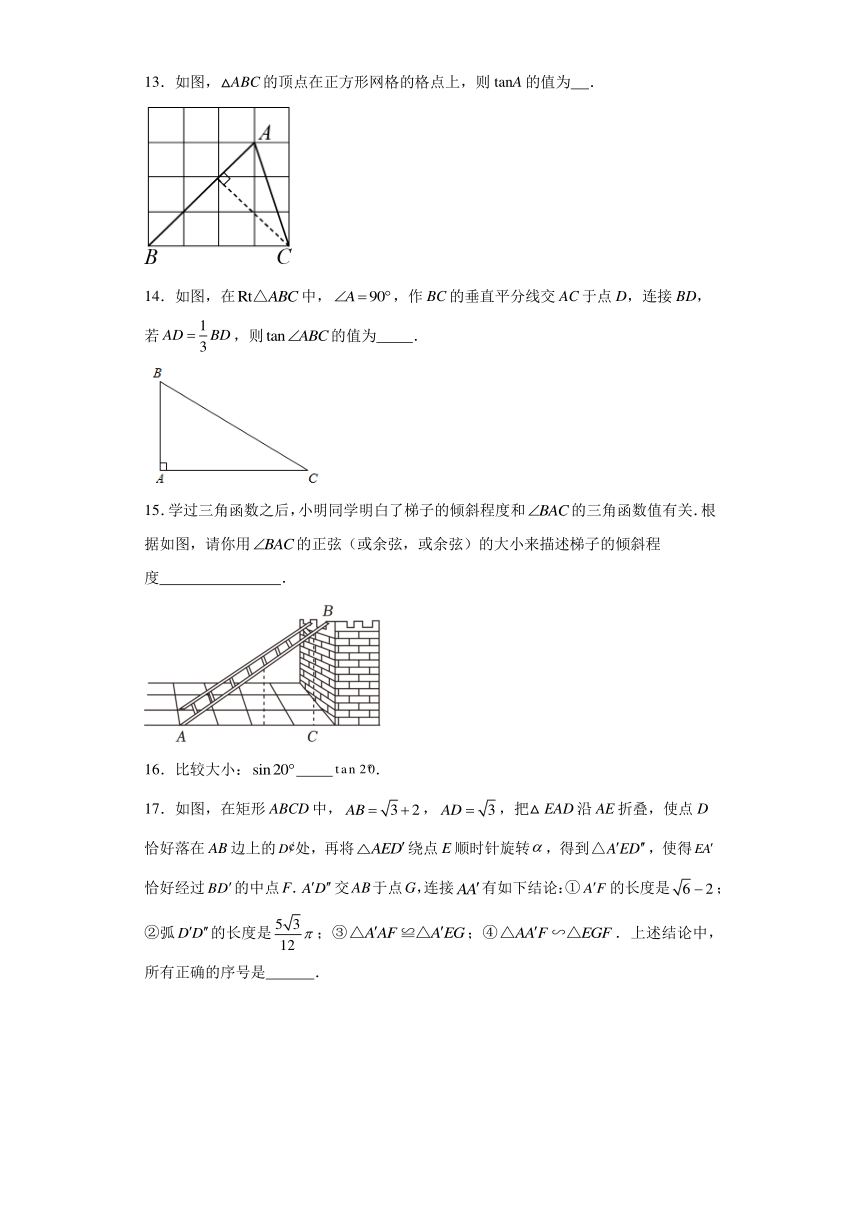
13.如图,△ABC的顶点在正方形网格的格点上,则tanA的值为 .
14.如图,在中,,作BC的垂直平分线交AC于点D,连接BD,若,则的值为 .
15.学过三角函数之后,小明同学明白了梯子的倾斜程度和的三角函数值有关.根据如图,请你用的正弦(或余弦,或余弦)的大小来描述梯子的倾斜程度 .
16.比较大小: .
17.如图,在矩形ABCD中,,,把△EAD沿AE折叠,使点D恰好落在AB边上的处,再将绕点E顺时针旋转,得到,使得恰好经过的中点F.交AB于点G,连接有如下结论:①的长度是;②弧的长度是;③;④.上述结论中,所有正确的序号是 .
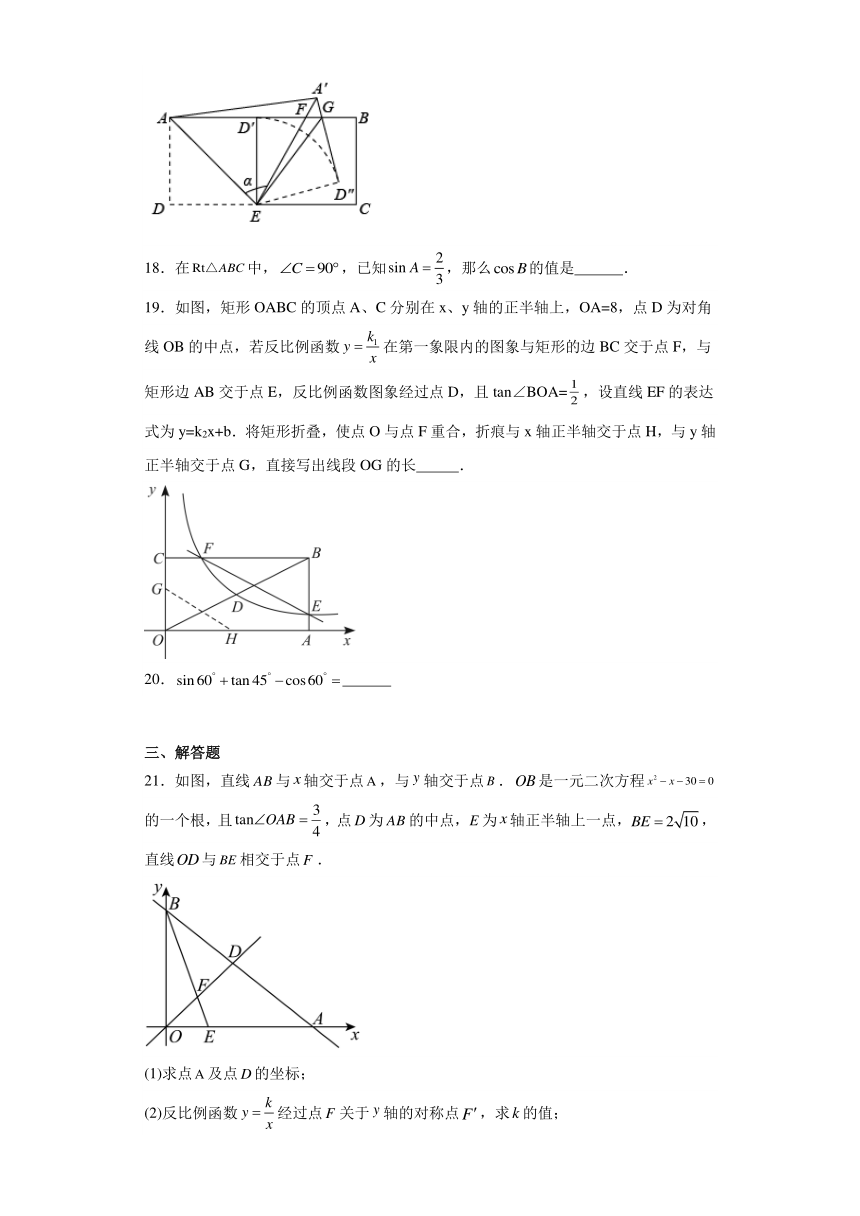
18.在中,,已知,那么的值是 .
19.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,OA=8,点D为对角线OB的中点,若反比例函数在第一象限内的图象与矩形的边BC交于点F,与矩形边AB交于点E,反比例函数图象经过点D,且tan∠BOA=,设直线EF的表达式为y=k2x+b.将矩形折叠,使点O与点F重合,折痕与x轴正半轴交于点H,与y轴正半轴交于点G,直接写出线段OG的长 .
20.
三、解答题
21.如图,直线与轴交于点,与轴交于点.是一元二次方程的一个根,且,点为的中点,为轴正半轴上一点,,直线与相交于点.
(1)求点及点的坐标;
(2)反比例函数经过点关于轴的对称点,求的值;
(3)在直线上是否存在点,使为等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
22.计算:
23.如图,直线经过点A(-3,0)与y轴正半轴交于B,在x轴正半轴上有一点D,且tan过D点作DC⊥x轴交直线于C点,反比例函数经过点C
(1)求b和反比例函数的解析式
(2)将点B向右平移m个单位长度得到点P,当四边形BCPD为菱形时,求出m的值,并判断点P是否落在反比例函数图象上.
(3)点E是x轴上一点,且△COE是等腰三角形,求所有点E的坐标.
24.矩形中,,分别以所在直线为x轴,y轴,建立如图所示的平面直角坐标系,F是边上一个动点(不与B,C重合),过点F的反比例函数的图象与边交于点E.
(1)当点F为边的中点时,求点E的坐标;
(2)连接,求的正切值.
25.如图,在中,,是边上一点,以为圆心的半圆分别与、边相切于、两点,连接.已知,.
求:(1);
(2)图中两部分阴影面积的和.
参考答案:
1.A
2.C
3.D
4.B
5.D
6.D
7.C
8.D
9.B
10.B
11.
12.
13.2.
14.
15.的正弦值越大,梯子越陡
16.
17.①②④
18.
19.
20.
21.(1)
(2)
(3)存在,点P的坐标为或或或.
22.0
23.(1)b=4,;(2)m=6,点P在反比例函数图象上;(2)
24.(1)
(2)
25.(1) ;(2) 图中两部分阴影面积的和为.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,△ABC中,BD平分∠ABC,BC的垂直平分线交BC于点E,交BD于点F,连接CF.若∠ACF=2∠ABD,∠BFC=132°,则cosA的值为 ( )
A. B. C. D.
2.角,满足,下列是关于角,的命题,其中错误的是( )
A. B. C. D.
3.计算的值等于( )
A. B.
C. D.
4.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A=,那么CD的长为( )
A. B.
C. D.
5.矩形纸片中,E为的中点,连接,将沿折叠得到,连接.若,,则的长是( )
A.3 B. C. D.
6.如图,在中,,,,,则下列选项正确的是( )
A. B. C. D.
7.已知锐角α,且sinα=cos38°,则α=( )
A.38° B.62° C.52° D.72°
8.如图,网格中小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( ).
A. B. C. D.
9.在中,,,则( )
A. B. C. D.
10.如图,已知 两点的坐标分别为,点分别是直线和x轴上的动点,,点是线段的中点,连接交轴于点;当⊿面积取得最小值时,的值是( )
A. B. C. D.
二、填空题
11.在三角形ABC中,AB=4,tanC=1,那么BC+AC的最大值为 .
12.如图,△ABC内接于圆O,若圆的半径是2.5,AB=3,则∠C的正切值= .
13.如图,△ABC的顶点在正方形网格的格点上,则tanA的值为 .
14.如图,在中,,作BC的垂直平分线交AC于点D,连接BD,若,则的值为 .
15.学过三角函数之后,小明同学明白了梯子的倾斜程度和的三角函数值有关.根据如图,请你用的正弦(或余弦,或余弦)的大小来描述梯子的倾斜程度 .
16.比较大小: .
17.如图,在矩形ABCD中,,,把△EAD沿AE折叠,使点D恰好落在AB边上的处,再将绕点E顺时针旋转,得到,使得恰好经过的中点F.交AB于点G,连接有如下结论:①的长度是;②弧的长度是;③;④.上述结论中,所有正确的序号是 .
18.在中,,已知,那么的值是 .
19.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,OA=8,点D为对角线OB的中点,若反比例函数在第一象限内的图象与矩形的边BC交于点F,与矩形边AB交于点E,反比例函数图象经过点D,且tan∠BOA=,设直线EF的表达式为y=k2x+b.将矩形折叠,使点O与点F重合,折痕与x轴正半轴交于点H,与y轴正半轴交于点G,直接写出线段OG的长 .
20.
三、解答题
21.如图,直线与轴交于点,与轴交于点.是一元二次方程的一个根,且,点为的中点,为轴正半轴上一点,,直线与相交于点.
(1)求点及点的坐标;
(2)反比例函数经过点关于轴的对称点,求的值;
(3)在直线上是否存在点,使为等腰三角形?若存在,直接写出点的坐标;若不存在,请说明理由.
22.计算:
23.如图,直线经过点A(-3,0)与y轴正半轴交于B,在x轴正半轴上有一点D,且tan过D点作DC⊥x轴交直线于C点,反比例函数经过点C
(1)求b和反比例函数的解析式
(2)将点B向右平移m个单位长度得到点P,当四边形BCPD为菱形时,求出m的值,并判断点P是否落在反比例函数图象上.
(3)点E是x轴上一点,且△COE是等腰三角形,求所有点E的坐标.
24.矩形中,,分别以所在直线为x轴,y轴,建立如图所示的平面直角坐标系,F是边上一个动点(不与B,C重合),过点F的反比例函数的图象与边交于点E.
(1)当点F为边的中点时,求点E的坐标;
(2)连接,求的正切值.
25.如图,在中,,是边上一点,以为圆心的半圆分别与、边相切于、两点,连接.已知,.
求:(1);
(2)图中两部分阴影面积的和.
参考答案:
1.A
2.C
3.D
4.B
5.D
6.D
7.C
8.D
9.B
10.B
11.
12.
13.2.
14.
15.的正弦值越大,梯子越陡
16.
17.①②④
18.
19.
20.
21.(1)
(2)
(3)存在,点P的坐标为或或或.
22.0
23.(1)b=4,;(2)m=6,点P在反比例函数图象上;(2)
24.(1)
(2)
25.(1) ;(2) 图中两部分阴影面积的和为.
