28.2解直角三角形及其应用同步练习(含简单答案)人教版(2012)数学九年级下册
文档属性
| 名称 | 28.2解直角三角形及其应用同步练习(含简单答案)人教版(2012)数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 628.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 14:11:14 | ||
图片预览


文档简介
28.2解直角三角形及其应用同步练习人教版(2012)数学九年级下册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
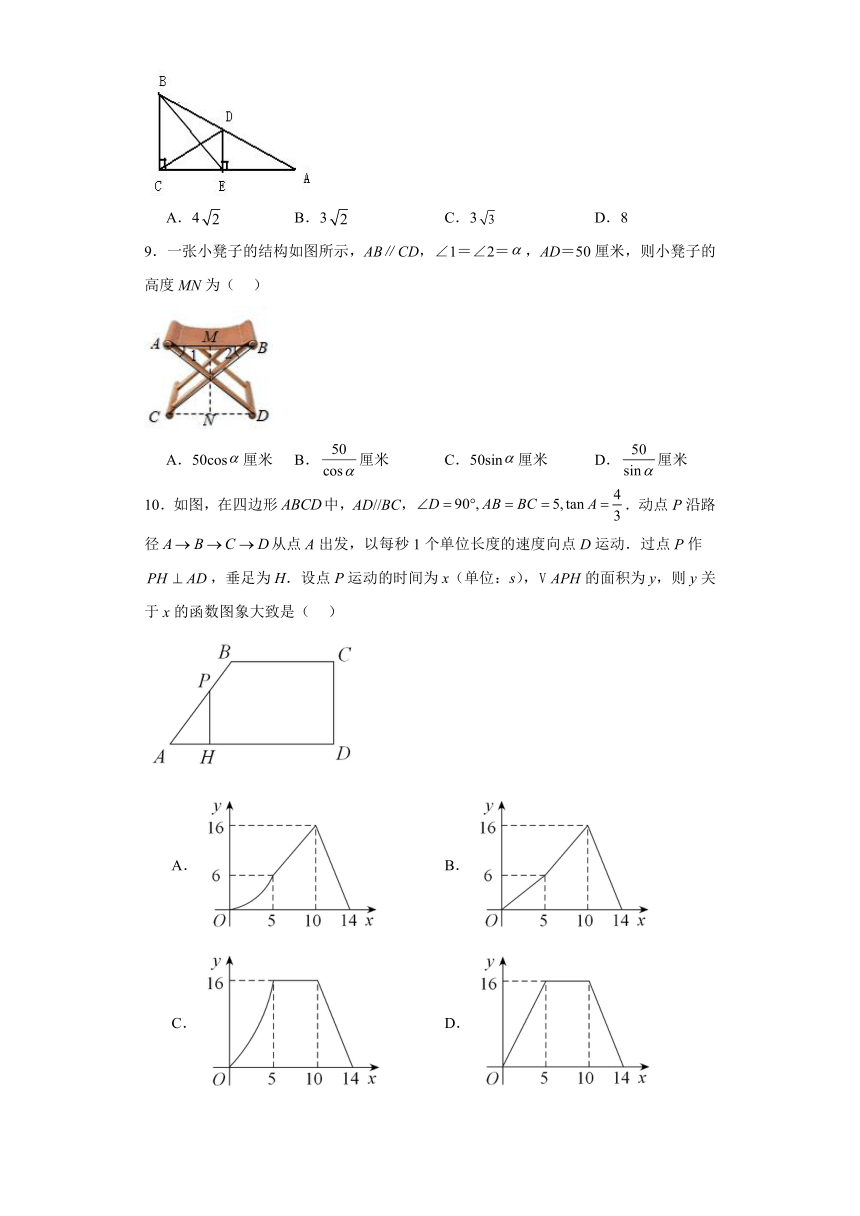
1.如图,将绕点A按顺时针方向旋转一定角度得到,点B的对应点D恰好落在边上.若,则的长为( )
A.0.5 B.1.5 C. D.1
2.如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为α,A处到地面B处的距离AB=35m,则两栋楼之间的距离BC(单位:m)为( )
A.35tanα B.35sinα C. D.
3.如图,点,,在上,若四边形是平行四边形,的半径为,则的长是( )
A. B. C. D.
4.如图,在中,M是上一点,E是上一动点,过点E作交于点F,若,,,则的最大值为( )
A.40 B.30 C.20 D.15
5.如图,在铁路建设中,需要确定隧道两洞口A和B的距离.点D,点E分别位于测绘点C的正北和正西方向.已知测得两定位点E和D与隧道口A和B的距离分别为和,测绘点H,G分别为,的中点,测绘方在测绘点H测得点G在点H的南偏西的方向上,且,则隧道的长约为( )(参考数据:)
A.1600m B.1300m C.980m D.900m
6.如图,是的内接三角形,,,连接,,则的长是( )
A. B. C. D.
7.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. B. C. D.
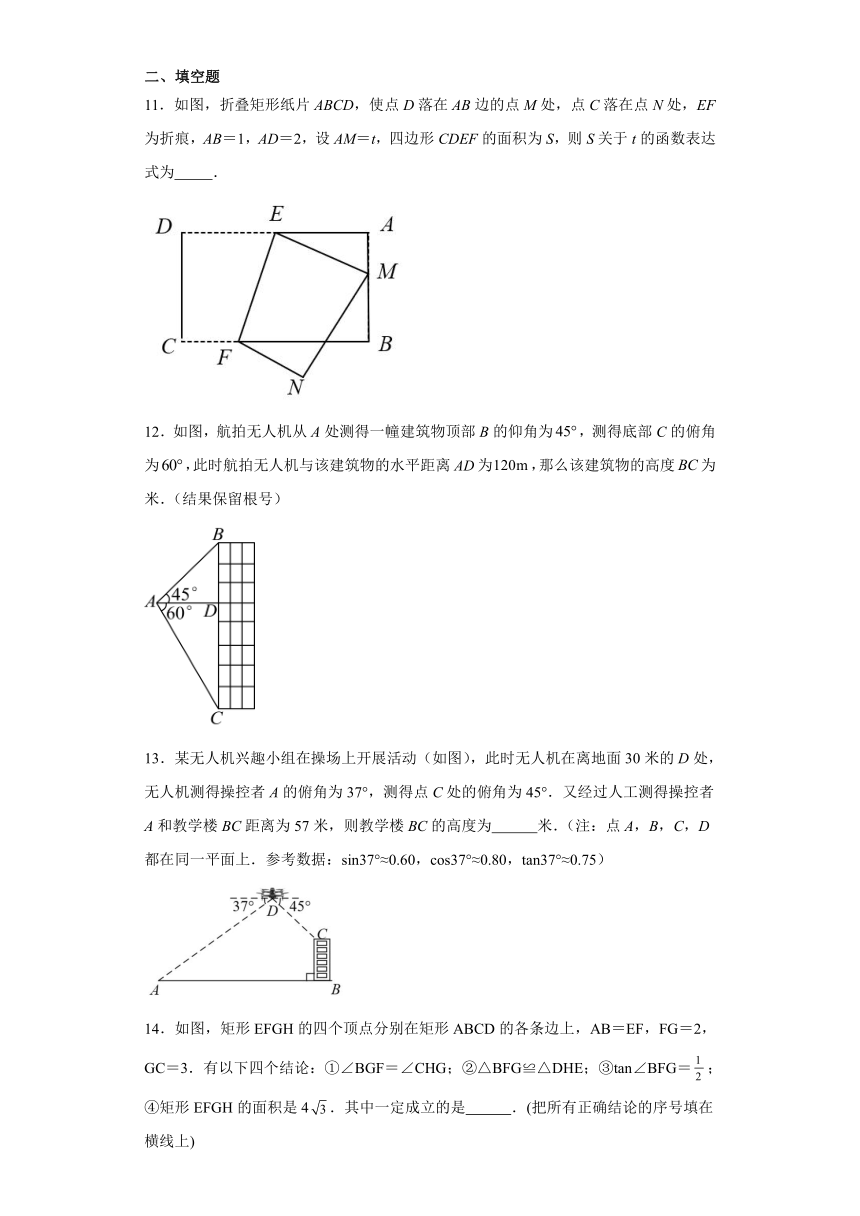
8.如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE⊥AC于E,若DE=2,CD=2,则BE的长为( )
A.4 B.3 C.3 D.8
9.一张小凳子的结构如图所示,AB∥CD,∠1=∠2=,AD=50厘米,则小凳子的高度MN为( )
A.50cos厘米 B.厘米 C.50sin厘米 D.厘米
10.如图,在四边形中,AD//BC,.动点P沿路径从点A出发,以每秒1个单位长度的速度向点D运动.过点P作,垂足为H.设点P运动的时间为x(单位:s),的面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
二、填空题
11.如图,折叠矩形纸片ABCD,使点D落在AB边的点M处,点C落在点N处,EF为折痕,AB=1,AD=2,设AM=t,四边形CDEF的面积为S,则S关于t的函数表达式为 .
12.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为,测得底部C的俯角为,此时航拍无人机与该建筑物的水平距离为,那么该建筑物的高度为 米.(结果保留根号)
13.某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测得操控者A和教学楼BC距离为57米,则教学楼BC的高度为 米.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
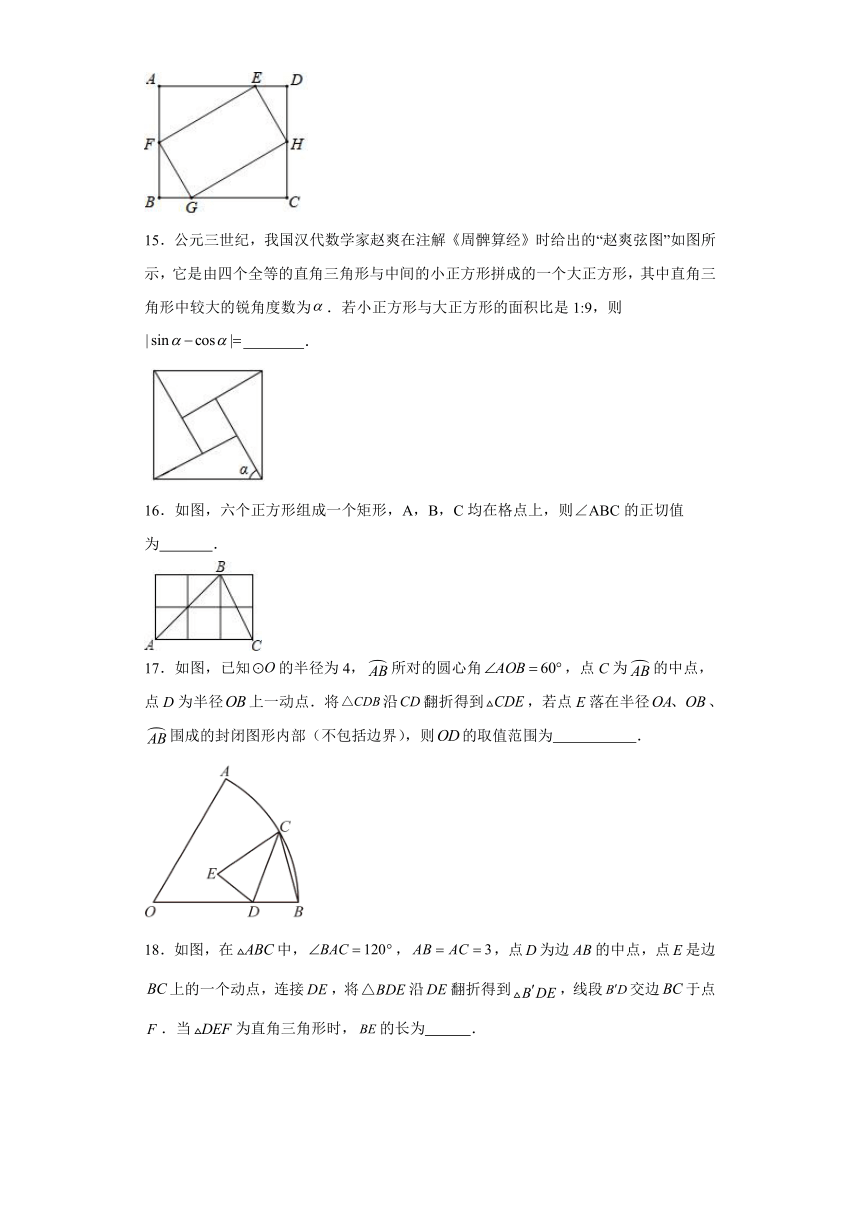
14.如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=;④矩形EFGH的面积是4.其中一定成立的是 .(把所有正确结论的序号填在横线上)
15.公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,其中直角三角形中较大的锐角度数为.若小正方形与大正方形的面积比是1:9,则 .
16.如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为 .
17.如图,已知的半径为4,所对的圆心角,点C为的中点,点D为半径上一动点.将沿翻折得到,若点E落在半径、围成的封闭图形内部(不包括边界),则的取值范围为 .
18.如图,在中,,,点为边的中点,点是边上的一个动点,连接,将沿翻折得到,线段交边于点.当为直角三角形时,的长为 .
19.如图,在⊙O中,弦AB的长为,圆心到弦AB的距离为1,则∠BOC的度数为 .
20.如图,在中,,,,点分别在两边上,将沿直线折叠,使点的对应点D恰好落在线段BC上,当是直角三角形时,则的值为 .
三、解答题
21.如图,小明一家从家所在地自驾前往古镇游玩,古镇在小明家的正北方向千米处,由于道路清障,小明一家先从沿西北方向行驶至地,再从地沿北偏东方向行驶至古镇,求小明一家从地到地实际行驶的路程是多少千米?(结果精确到千米)
(参考数据:,,,)
22.为了迎接2023年的“亚洲杯”足球联赛,某市设计了如图1所示的足球场,足球场看台上方是挡雨棚.将看台和挡雨棚的剖面图简化成如图2所示的平面图形.看台ABC是直角三角形,∠B=90°,线段MN是挡雨棚DE的固定拉索,点M、D在直线BC上,过挡雨棚端点E作水平地面AB的垂线段EF,垂足为F.测得点E在点D的北偏西75°方向,∠CAB=30,米,BC=9米,连接DF,已知.根据题意,求:
(1)看台顶端C与雨棚端点D之间的距离CD的长:
(2)为了不影响球迷观看比赛的效果,要求挡雨棚端点E到地面AB的垂直高度EF不小于16.5米.请通过计算说明这一设计是否符合要求.(参考数据)
23.如图,某小组为测量某幢大厦AB的高度,他们在地面C处测得另一幢大厦DE的项部E处的仰角∠ECD=32°.登上大厦DE的项部E处后,测得该大厦AB的顶部A处的仰角为60°.已知C、D、B三点在同一水平直线上,且CD=180米,DB=120米.
(1)求大厦DE的高度(结果精确到个位):
(2)求大厦AB的高度(结果精确到个位).(参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62,=1.41,=1.73)
24.嵩岳寺塔位于登封市区西北6千米嵩山南麓嵩岳寺院内,为北魏时期佛塔.该塔是我国现存最早的砖塔,反映了中外建筑文化交流融合创新的历程,在结构、造型等方面具有很大价值,对后世砖塔建筑有着巨大影响.某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
课题 测量嵩岳寺塔的高度
测量工具 测量角度的仪器,皮尺等
测量方案 在点C处放置高为1.3米的测角仪CD,此时测得塔顶端A的仰角为45°,再沿BC方向走22米到达点E处,此时测得塔顶端A的仰角为32°. 说明:点E、C、B三点在同一水平线上.
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔AB的高度.(精确到0.1米,参考数据:,,)
25.在一次综合实践活动中,数学兴趣小组的同学想要测量一楼房的高度.如图,楼房后有一假山,其斜坡坡比为1:,山坡坡面上点处有一休息亭,在此处测得楼顶的仰角为45°,假山坡脚与楼房水平距离米,与亭子距离米.
(1)求点距水平地面的高度;
(2)求楼房的高.(结果精确到整数,参考数据≈1.414,≈1.732).
参考答案:
1.D
2.D
3.C
4.B
5.B
6.D
7.D
8.A
9.C
10.A
11.S=t2﹣t+1
12./
13.13
14.①②④
15.
16.3.
17.
18.或或
19.60°
20.1或2.
21.从地到地实际行驶的路程是千米
22.(1)3米
(2)设计符合要求
23.(1)大厦DE的高度为112米
(2)大厦AB的高度为米
24.嵩岳寺塔的高度约为37.2m
25.(1)米;(2)点距水平地面的高度为15米;楼房的高约为61米
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,将绕点A按顺时针方向旋转一定角度得到,点B的对应点D恰好落在边上.若,则的长为( )
A.0.5 B.1.5 C. D.1
2.如图,小明站在自家阳台上A处观测到对面大楼底部C的俯角为α,A处到地面B处的距离AB=35m,则两栋楼之间的距离BC(单位:m)为( )
A.35tanα B.35sinα C. D.
3.如图,点,,在上,若四边形是平行四边形,的半径为,则的长是( )
A. B. C. D.
4.如图,在中,M是上一点,E是上一动点,过点E作交于点F,若,,,则的最大值为( )
A.40 B.30 C.20 D.15
5.如图,在铁路建设中,需要确定隧道两洞口A和B的距离.点D,点E分别位于测绘点C的正北和正西方向.已知测得两定位点E和D与隧道口A和B的距离分别为和,测绘点H,G分别为,的中点,测绘方在测绘点H测得点G在点H的南偏西的方向上,且,则隧道的长约为( )(参考数据:)
A.1600m B.1300m C.980m D.900m
6.如图,是的内接三角形,,,连接,,则的长是( )
A. B. C. D.
7.在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A. B. C. D.
8.如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,DE⊥AC于E,若DE=2,CD=2,则BE的长为( )
A.4 B.3 C.3 D.8
9.一张小凳子的结构如图所示,AB∥CD,∠1=∠2=,AD=50厘米,则小凳子的高度MN为( )
A.50cos厘米 B.厘米 C.50sin厘米 D.厘米
10.如图,在四边形中,AD//BC,.动点P沿路径从点A出发,以每秒1个单位长度的速度向点D运动.过点P作,垂足为H.设点P运动的时间为x(单位:s),的面积为y,则y关于x的函数图象大致是( )
A. B.
C. D.
二、填空题
11.如图,折叠矩形纸片ABCD,使点D落在AB边的点M处,点C落在点N处,EF为折痕,AB=1,AD=2,设AM=t,四边形CDEF的面积为S,则S关于t的函数表达式为 .
12.如图,航拍无人机从A处测得一幢建筑物顶部B的仰角为,测得底部C的俯角为,此时航拍无人机与该建筑物的水平距离为,那么该建筑物的高度为 米.(结果保留根号)
13.某无人机兴趣小组在操场上开展活动(如图),此时无人机在离地面30米的D处,无人机测得操控者A的俯角为37°,测得点C处的俯角为45°.又经过人工测得操控者A和教学楼BC距离为57米,则教学楼BC的高度为 米.(注:点A,B,C,D都在同一平面上.参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
14.如图,矩形EFGH的四个顶点分别在矩形ABCD的各条边上,AB=EF,FG=2,GC=3.有以下四个结论:①∠BGF=∠CHG;②△BFG≌△DHE;③tan∠BFG=;④矩形EFGH的面积是4.其中一定成立的是 .(把所有正确结论的序号填在横线上)
15.公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,其中直角三角形中较大的锐角度数为.若小正方形与大正方形的面积比是1:9,则 .
16.如图,六个正方形组成一个矩形,A,B,C均在格点上,则∠ABC的正切值为 .
17.如图,已知的半径为4,所对的圆心角,点C为的中点,点D为半径上一动点.将沿翻折得到,若点E落在半径、围成的封闭图形内部(不包括边界),则的取值范围为 .
18.如图,在中,,,点为边的中点,点是边上的一个动点,连接,将沿翻折得到,线段交边于点.当为直角三角形时,的长为 .
19.如图,在⊙O中,弦AB的长为,圆心到弦AB的距离为1,则∠BOC的度数为 .
20.如图,在中,,,,点分别在两边上,将沿直线折叠,使点的对应点D恰好落在线段BC上,当是直角三角形时,则的值为 .
三、解答题
21.如图,小明一家从家所在地自驾前往古镇游玩,古镇在小明家的正北方向千米处,由于道路清障,小明一家先从沿西北方向行驶至地,再从地沿北偏东方向行驶至古镇,求小明一家从地到地实际行驶的路程是多少千米?(结果精确到千米)
(参考数据:,,,)
22.为了迎接2023年的“亚洲杯”足球联赛,某市设计了如图1所示的足球场,足球场看台上方是挡雨棚.将看台和挡雨棚的剖面图简化成如图2所示的平面图形.看台ABC是直角三角形,∠B=90°,线段MN是挡雨棚DE的固定拉索,点M、D在直线BC上,过挡雨棚端点E作水平地面AB的垂线段EF,垂足为F.测得点E在点D的北偏西75°方向,∠CAB=30,米,BC=9米,连接DF,已知.根据题意,求:
(1)看台顶端C与雨棚端点D之间的距离CD的长:
(2)为了不影响球迷观看比赛的效果,要求挡雨棚端点E到地面AB的垂直高度EF不小于16.5米.请通过计算说明这一设计是否符合要求.(参考数据)
23.如图,某小组为测量某幢大厦AB的高度,他们在地面C处测得另一幢大厦DE的项部E处的仰角∠ECD=32°.登上大厦DE的项部E处后,测得该大厦AB的顶部A处的仰角为60°.已知C、D、B三点在同一水平直线上,且CD=180米,DB=120米.
(1)求大厦DE的高度(结果精确到个位):
(2)求大厦AB的高度(结果精确到个位).(参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62,=1.41,=1.73)
24.嵩岳寺塔位于登封市区西北6千米嵩山南麓嵩岳寺院内,为北魏时期佛塔.该塔是我国现存最早的砖塔,反映了中外建筑文化交流融合创新的历程,在结构、造型等方面具有很大价值,对后世砖塔建筑有着巨大影响.某数学兴趣小组通过调查研究把“如何测量嵩岳寺塔的高度”作为一项课题活动,他们制订了测量方案,并利用课余时间实地测量.
课题 测量嵩岳寺塔的高度
测量工具 测量角度的仪器,皮尺等
测量方案 在点C处放置高为1.3米的测角仪CD,此时测得塔顶端A的仰角为45°,再沿BC方向走22米到达点E处,此时测得塔顶端A的仰角为32°. 说明:点E、C、B三点在同一水平线上.
请你根据表中信息结合示意图帮助该数学兴趣小组求嵩岳寺塔AB的高度.(精确到0.1米,参考数据:,,)
25.在一次综合实践活动中,数学兴趣小组的同学想要测量一楼房的高度.如图,楼房后有一假山,其斜坡坡比为1:,山坡坡面上点处有一休息亭,在此处测得楼顶的仰角为45°,假山坡脚与楼房水平距离米,与亭子距离米.
(1)求点距水平地面的高度;
(2)求楼房的高.(结果精确到整数,参考数据≈1.414,≈1.732).
参考答案:
1.D
2.D
3.C
4.B
5.B
6.D
7.D
8.A
9.C
10.A
11.S=t2﹣t+1
12./
13.13
14.①②④
15.
16.3.
17.
18.或或
19.60°
20.1或2.
21.从地到地实际行驶的路程是千米
22.(1)3米
(2)设计符合要求
23.(1)大厦DE的高度为112米
(2)大厦AB的高度为米
24.嵩岳寺塔的高度约为37.2m
25.(1)米;(2)点距水平地面的高度为15米;楼房的高约为61米
