新人教版数学八年级下册第十九章一次函数19.1.2《函数图像》课时练习.doc
文档属性
| 名称 | 新人教版数学八年级下册第十九章一次函数19.1.2《函数图像》课时练习.doc |

|
|
| 格式 | doc | ||
| 文件大小 | 155.0KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 00:00:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
新人教版数学八年级下册第十九章19.1.2函数图象课时练习
一、选择题(每小题5分,共30分)
1.下列函数关系中,属于正比例函数关系的是( )
A.圆的面积与它的半径
B.面积为常数S时矩形的长y与宽x
C.路程是常数时,行驶的速度v与时间t
D. 三角形的底边是常数a时它的面积S与这条边上的高h
答案:D.
知识点:函数的图象
解析:解答:A.s=πr,s是r的二次函数
B.y=,y是x的反比例函数
C.v=,v是t的反比例函数
D.s=ah,s是h的正比例函数
分析:将每个选项的关系式列出来,然后再判断即可.
故选D.
2.一枝蜡烛长20厘米,点燃后每小时燃烧掉 ( http: / / www.21cnjy.com )5厘米,则下列3幅图象中能大致刻画出这支蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).【来源:21·世纪·教育·网】
答案:C.
知识点:函数的图象
解析:解答:设蜡烛点燃后剩下h厘米时,燃烧了t小时,
则h与t的关系是h=20-5t,是一次函数图象,即t越大,h越小,
符合此条件的只有C.
分析:可以列出蜡烛点燃后,剩下的长度h与点燃时间t的函数关系式,利用函数的性质判断即可.
故选C.
3.下列四个点中在函数y=2x-3的图象上有( )个.(1,2) , (3,3) , (-1, -1), (1.5,0)
A.1 B.2 C.3 D.4
答案:B.
知识点:函数的图象
解析:解答:分别代入:
2≠2×1-3;3=2×3-3;-1≠2×(-1)-3;0=2×1.5-3;共两个满足.
分析:分别将各选项代入函数关系式,能满足左边等于右边的即在函数图象上.
故选B.
4.如果A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
A .A比B先出发 B.A、B两人的速度相同 C.A先到达终点 D.B比A跑的路程多
答案:C.
知识点:函数的图象
解析:解答:结合图象可得出,A、B同时出发,A比B先到达终点,A的速度比B的速度快.
分析:根据图象法表示函数,观察A、B的出发时间相同.
故选C.
5.函数y=3x+1的图象一定经过 ( )
A.(2,7) B.(4,10) C.(3,5) D.(-2,3)
答案:A.
知识点:函数的图象
解析:解答:将A、B、C、D的坐标分别代入解析式只A符合左边等右边,故A选项正确.
分析:将ABCD各点分别代入解析式,使等式成立的即为函数图象上的点.
故选A.
6.下列各点中,在函数y=2x-6的图象上的是( )
A.(-2,3) B.(3,-2) C.(1,4) D.(4,2)
答案:D.
知识点:函数的图象
解析:解答:将A、B、C、D的坐标分别代入解析式只D符合左边等右边,故D选项正确.
分析:将ABCD各点分别代入解析式,使等式成立的即为函数图象上的点.
故选D.
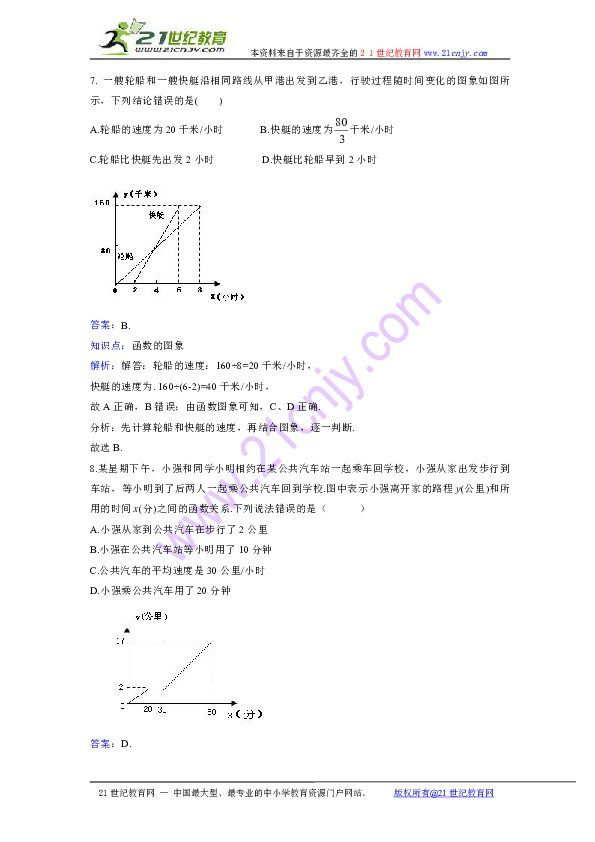
7. 一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )
A.轮船的速度为20千米/小时 B.快艇的速度为千米/小时
C.轮船比快艇先出发2小时 D.快艇比轮船早到2小时
答案:B.
知识点:函数的图象
解析:解答:轮船的速度:160÷8=20千米/小时,
快艇的速度为. 160÷(6-2)=40千米/小时,
故A正确,B错误;由函数图象可知,C、D正确.
分析:先计算轮船和快艇的速度,再结合图象,逐一判断.
故选B.
8.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
A.小强从家到公共汽车在步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
答案:D.
知识点:函数的图象
解析:解答:A.依题意得小强从家到公共汽车步行了2公里,故选项正确;
B.依题意得小强在公共汽车站等掌上小明用了10分钟,故选项正确;
C.公交车的速度为30公里/小时,故选项正确;
D.小强和小明一起乘坐公共汽车,时间为30分钟,故选项错误.
分析:根据图象可以确定小强离公共汽车站2公里,步行用了多长时间,等公交车的时间是多少,两人乘车运行的时间和对应的路程,然后确定各自的速度.
故选D.
9.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反应当天爷爷离家的距离y(米)与时间t(分钟)之间的大致图象是( )
A.B.C.D.
答案:B.
知识点:函数的图象
解析:解答:根据题意中信息可知,相同的路程,跑步比漫步的速度快;在一定时间内没有移动距离,则速度为0.故小华的爷爷跑步到公园的速度最快,即单位时间内通过的路程最大,打太极的过程中没有移动距离,因此通过的路程为0,还要注意出去和回来时的方向不同,故B符合要求.
分析:生活中比较运动快慢通常有两种方法,即比较相同时间内通过的路程多少或通过相同路程所用时间的多少,但统一的方法是直接比较速度的大小.
故选B.
10.如图,某个函数的图象由线段AB和BC组成,其中点A(0,),B(1,),C(2,),由此函数的最小值是( )
A.0 B. C.1 D.
答案:B.
知识点:函数的图象
解析:解答:由函数图象的纵坐标,得
>>.
分析:根据函数图象的纵坐标,可得答案.
故选B.
11.均匀地向如图的容器中注满水,能反应在注水过程中水面高度h随时间t变化的图象是( )
A. B. C. D.
答案:A.
知识点:函数的图象
解析:解答:最下面的容器较粗,第二个容器最粗,那么第二阶段的函数图象水面高度h随时间t的增大而增长缓慢,用时较长,最上面容器最小,那么用时最短.
分析:由于三个容器的高度相同,粗细不同,那么水面高度h随时间t变化而分三个阶段.
故选A.
12.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数的图象,那么符合小明行驶情况的图象大致是( )
A.B.C.D.
答案:D.
知识点:函数的图象
解析:解答:因为开始以正常速度匀速行驶――停下修车――加快速度行驶,可得S先缓慢减小,再不变,再加速减小.
分析:由于开始以正常速度行驶,接着停下修车,后来加快速度匀速,所以开始行驶路S是均匀减小的,接着不变,后来速度加快,所以S变化也加快变小,由此即可作出选择.
故选D.
13.小亮家与学校相距1500m,一天放学后他步行回家,最初以某一速度匀速前进,途中遇到熟人小强,说话耽误几分钟,与小强告别后他就改为匀速慢跑,最后回到了家,设小亮从学校出发后所用的时间为t(min),与家的距离为s(m),下列图象中,能表示上述过程的是( )
A. B.C.D.
答案:C.
知识点:函数的图象
解析:解答:由题意得,最初与家的距离s随时间t的增大而减小,与小强说话时,时间增大而s不变,慢跑时,与家的距离s随时间t的增大而减小.
分析:分三段分析,最初步行、与小强说话、匀速慢跑,分析函数的性质,进行判断即可.
故选C.
14.如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是
( )
A.B.C.D.
答案:D.
知识点:函数的图象
解析:解答:由题意,得锥形瓶中水满之前,水槽中水的高度为0,锥形瓶中水满之后,水槽中的水逐渐增加,水槽中的水满之后,水槽中的水的高度不变.
分析:根据锥形瓶中水满之前,水槽中水的高度为零,锥形瓶中水满之后,水槽中的水逐渐增加,水槽中水满之后,水槽中的水的高度不变.
故选D.
15.如图,李老师早晨出门锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )
A. B.C.D.
答案:D.
知识点:函数的图象
解析:解答:由题意,得
从M到A距离再增加,由A经B到C与M的距离都是半径,由B到M距离逐渐减少,故D符合题意.
分析:根据半圆的关系,可得从M到A距离再增加,由A经B到C与M的距离都是半径,由B到M距离逐渐减少,可得答案.
故选D.
二、填空题(每小题5分,共25分)
16.放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
答案:0.2
知识点:函数的图象
解析:解答:由纵坐标看出路程是2千米,
由横坐标看出时间是10分钟,
小明的骑车速度是=0.2(千米/分钟).
分析:根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得答案.
故答案为:0.2
17.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发 小时,快车追上慢车行驶了 千米,快车比慢车早 小时到达B地.
答案:2,276,4
知识点:函数的图象
解析:解答:由图象直接可得出:一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发2小时,快车追上慢车行驶了276千米,快车比慢车早4小时到达B地.
分析:根据横坐标的意义,分别分析得出即可.
故答案为:2,276,4.
18.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为 平方米.
答案:100
知识点:函数的图象
解析:解答:由纵坐标看出:休息前绿化面积是60平方米,休息后绿化面积160-60=100平方米.
分析:根据函数图象的纵坐标,即可求得.
故答案为:100.
19.某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升 元.
答案:7.09
知识点:函数的图象
解析:解答:单价=709÷100=7.09元.
分析:根据函数图象知道100升油花费了709元,由此可求出这种汽油的单价.
故答案为:7.09.
20.甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快 千米.
答案:0.4
知识点:函数的图象
解析:解答:根据图示知,甲的速度是:8÷(5-1)=2(千米/小时),
乙的速度是:8÷5=1.6(千米/小时).
则:2-1.6=0.4(千米/小时).
故答案是:0.4.
分析:根据“速度=路程÷时间”分别求甲、乙的速度,然后求其差.
故答案为:7.09元.
三、解答题(每题10分,共50分)
21.小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:
(1)小明家离超市的距离是 千米;
(2)小明在超市买东西时间为 小时;
(3)小明去超市时的速度是 千米/小时.
答案:解答:(1)由纵坐标看出,小明家离超市的距离是3千米;
(2)由横坐标看出到达超市是12,离开超市是72,在超市的时间为72-12=60分钟=1小时;
(3)由纵坐标看出,小明家离超市的距离是3千米,由横坐标看出到达超市是12分钟=0.2小时,小明去超市时的速度是3÷0.2=15千米/小时.
故答案为3,1,15.
知识点:函数的图象
解析:分析:(1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得答案;
(3)根据函数图象的纵坐标,可得距离,根据函数的横坐标,可得时间,根据路程与时间的关系,可得答案.
22.一次越野跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程s(米)与时间t(秒)的关系如图,结合结合图象,求图中S1和S0的位置.
答案:解答:由图象可得出:
(1)小刚比李明早到终点100秒;
(2)两匀速跑时,小刚的速度大于李明的速度;
∵×100-×100=150,
∴S1=2050,
∴S0=1450+×100=1750.
故答案为2050,1750.
知识点:函数的图象
解析:分析:(1)根据图象可得出小刚和李明第一次相遇的时间是100秒;小刚比李明早到终点100秒;两人匀速跑时,小刚的速度大于李明的速度;
(2)求得小刚和李明速度,再乘以相遇时间,两个路程相减即可得出两人的路程之差150.
23.李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下来聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a、b、c的值;
(2)求李老师从学校到家的总时间.
答案:解答:由图象可得出:
(1)李老师停留地点离他家的路程为:2000-900=1100(米),
900÷45=20(分).
a=20,b=1100,c=20+30=50;
(2)20+30+1100/110=60(分)
故答案为(1)a=20,b=1100,c=50(2)60分钟.
知识点:函数的图象
解析:分析:(1)根据函数图象和题中给出的信息算出a的值以及b、c的值;
(2)根据等式“时间=路程/速度”分段求出时间,再累加起来算出到家的时间.
24.小强骑自行车去交游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间的函数图象,根据图象所提供的数据,请你写出3个信息.
答案:解答:1.小强从早上9时出发;
2.他在10时30分开始第一次休息;
3.第一次休息11-10.5=0.5小时;
4.小强离家最远为30千米;
5.他在15时回到家等.
知识点:函数的图象
解析:分析:(1)一般应选取最容易得到的答案,比如什么时间出发,到达离家多远的地方;什么时候开始休息,休息了多长时间.
25.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
答案:解答:(1)学校距他家1000米,王老师用25分钟;
(2)王老师吃早餐用了20-10=10分钟;
(3)吃完早餐以后速度快,
(1000-500)÷(25-20)=100(米/分).
知识点:函数的图象
解析:分析:(1)由于步行前往学校,途中在路边一饭店吃早餐,那么行驶路程S(米)与时间t(分)之间的关系图象中有一段平行x轴的线段,然后学校,根据图象可以直接得到结论;(2)根据图象中平行线x轴的线段即可确定王老师吃早餐用了多少时间;
(3)根据图象可以分别求出吃早餐以前的速度和吃完早餐以后的速度,然后比较即可得到结果.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
新人教版数学八年级下册第十九章19.1.2函数图象课时练习
一、选择题(每小题5分,共30分)
1.下列函数关系中,属于正比例函数关系的是( )
A.圆的面积与它的半径
B.面积为常数S时矩形的长y与宽x
C.路程是常数时,行驶的速度v与时间t
D. 三角形的底边是常数a时它的面积S与这条边上的高h
答案:D.
知识点:函数的图象
解析:解答:A.s=πr,s是r的二次函数
B.y=,y是x的反比例函数
C.v=,v是t的反比例函数
D.s=ah,s是h的正比例函数
分析:将每个选项的关系式列出来,然后再判断即可.
故选D.
2.一枝蜡烛长20厘米,点燃后每小时燃烧掉 ( http: / / www.21cnjy.com )5厘米,则下列3幅图象中能大致刻画出这支蜡烛点燃后剩下的长度h(厘米)与点燃时间t之间的函数关系的是( ).【来源:21·世纪·教育·网】
答案:C.
知识点:函数的图象
解析:解答:设蜡烛点燃后剩下h厘米时,燃烧了t小时,
则h与t的关系是h=20-5t,是一次函数图象,即t越大,h越小,
符合此条件的只有C.
分析:可以列出蜡烛点燃后,剩下的长度h与点燃时间t的函数关系式,利用函数的性质判断即可.
故选C.
3.下列四个点中在函数y=2x-3的图象上有( )个.(1,2) , (3,3) , (-1, -1), (1.5,0)
A.1 B.2 C.3 D.4
答案:B.
知识点:函数的图象
解析:解答:分别代入:
2≠2×1-3;3=2×3-3;-1≠2×(-1)-3;0=2×1.5-3;共两个满足.
分析:分别将各选项代入函数关系式,能满足左边等于右边的即在函数图象上.
故选B.
4.如果A、B两人在一次百米赛跑中,路程s(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
A .A比B先出发 B.A、B两人的速度相同 C.A先到达终点 D.B比A跑的路程多
答案:C.
知识点:函数的图象
解析:解答:结合图象可得出,A、B同时出发,A比B先到达终点,A的速度比B的速度快.
分析:根据图象法表示函数,观察A、B的出发时间相同.
故选C.
5.函数y=3x+1的图象一定经过 ( )
A.(2,7) B.(4,10) C.(3,5) D.(-2,3)
答案:A.
知识点:函数的图象
解析:解答:将A、B、C、D的坐标分别代入解析式只A符合左边等右边,故A选项正确.
分析:将ABCD各点分别代入解析式,使等式成立的即为函数图象上的点.
故选A.
6.下列各点中,在函数y=2x-6的图象上的是( )
A.(-2,3) B.(3,-2) C.(1,4) D.(4,2)
答案:D.
知识点:函数的图象
解析:解答:将A、B、C、D的坐标分别代入解析式只D符合左边等右边,故D选项正确.
分析:将ABCD各点分别代入解析式,使等式成立的即为函数图象上的点.
故选D.
7. 一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )
A.轮船的速度为20千米/小时 B.快艇的速度为千米/小时
C.轮船比快艇先出发2小时 D.快艇比轮船早到2小时
答案:B.
知识点:函数的图象
解析:解答:轮船的速度:160÷8=20千米/小时,
快艇的速度为. 160÷(6-2)=40千米/小时,
故A正确,B错误;由函数图象可知,C、D正确.
分析:先计算轮船和快艇的速度,再结合图象,逐一判断.
故选B.
8.某星期下午,小强和同学小明相约在某公共汽车站一起乘车回学校,小强从家出发步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中表示小强离开家的路程y(公里)和所用的时间x(分)之间的函数关系.下列说法错误的是( )
A.小强从家到公共汽车在步行了2公里
B.小强在公共汽车站等小明用了10分钟
C.公共汽车的平均速度是30公里/小时
D.小强乘公共汽车用了20分钟
答案:D.
知识点:函数的图象
解析:解答:A.依题意得小强从家到公共汽车步行了2公里,故选项正确;
B.依题意得小强在公共汽车站等掌上小明用了10分钟,故选项正确;
C.公交车的速度为30公里/小时,故选项正确;
D.小强和小明一起乘坐公共汽车,时间为30分钟,故选项错误.
分析:根据图象可以确定小强离公共汽车站2公里,步行用了多长时间,等公交车的时间是多少,两人乘车运行的时间和对应的路程,然后确定各自的速度.
故选D.
9.小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反应当天爷爷离家的距离y(米)与时间t(分钟)之间的大致图象是( )
A.B.C.D.
答案:B.
知识点:函数的图象
解析:解答:根据题意中信息可知,相同的路程,跑步比漫步的速度快;在一定时间内没有移动距离,则速度为0.故小华的爷爷跑步到公园的速度最快,即单位时间内通过的路程最大,打太极的过程中没有移动距离,因此通过的路程为0,还要注意出去和回来时的方向不同,故B符合要求.
分析:生活中比较运动快慢通常有两种方法,即比较相同时间内通过的路程多少或通过相同路程所用时间的多少,但统一的方法是直接比较速度的大小.
故选B.
10.如图,某个函数的图象由线段AB和BC组成,其中点A(0,),B(1,),C(2,),由此函数的最小值是( )
A.0 B. C.1 D.
答案:B.
知识点:函数的图象
解析:解答:由函数图象的纵坐标,得
>>.
分析:根据函数图象的纵坐标,可得答案.
故选B.
11.均匀地向如图的容器中注满水,能反应在注水过程中水面高度h随时间t变化的图象是( )
A. B. C. D.
答案:A.
知识点:函数的图象
解析:解答:最下面的容器较粗,第二个容器最粗,那么第二阶段的函数图象水面高度h随时间t的增大而增长缓慢,用时较长,最上面容器最小,那么用时最短.
分析:由于三个容器的高度相同,粗细不同,那么水面高度h随时间t变化而分三个阶段.
故选A.
12.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数的图象,那么符合小明行驶情况的图象大致是( )
A.B.C.D.
答案:D.
知识点:函数的图象
解析:解答:因为开始以正常速度匀速行驶――停下修车――加快速度行驶,可得S先缓慢减小,再不变,再加速减小.
分析:由于开始以正常速度行驶,接着停下修车,后来加快速度匀速,所以开始行驶路S是均匀减小的,接着不变,后来速度加快,所以S变化也加快变小,由此即可作出选择.
故选D.
13.小亮家与学校相距1500m,一天放学后他步行回家,最初以某一速度匀速前进,途中遇到熟人小强,说话耽误几分钟,与小强告别后他就改为匀速慢跑,最后回到了家,设小亮从学校出发后所用的时间为t(min),与家的距离为s(m),下列图象中,能表示上述过程的是( )
A. B.C.D.
答案:C.
知识点:函数的图象
解析:解答:由题意得,最初与家的距离s随时间t的增大而减小,与小强说话时,时间增大而s不变,慢跑时,与家的距离s随时间t的增大而减小.
分析:分三段分析,最初步行、与小强说话、匀速慢跑,分析函数的性质,进行判断即可.
故选C.
14.如图,将一个高度为12cm的锥形瓶放入一个空玻璃槽中,并向锥形瓶中匀速注水,若水槽的高度为10cm,则水槽中的水面高度y(cm)随注水时间x(s)的变化图象大致是
( )
A.B.C.D.
答案:D.
知识点:函数的图象
解析:解答:由题意,得锥形瓶中水满之前,水槽中水的高度为0,锥形瓶中水满之后,水槽中的水逐渐增加,水槽中的水满之后,水槽中的水的高度不变.
分析:根据锥形瓶中水满之前,水槽中水的高度为零,锥形瓶中水满之后,水槽中的水逐渐增加,水槽中水满之后,水槽中的水的高度不变.
故选D.
15.如图,李老师早晨出门锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )
A. B.C.D.
答案:D.
知识点:函数的图象
解析:解答:由题意,得
从M到A距离再增加,由A经B到C与M的距离都是半径,由B到M距离逐渐减少,故D符合题意.
分析:根据半圆的关系,可得从M到A距离再增加,由A经B到C与M的距离都是半径,由B到M距离逐渐减少,可得答案.
故选D.
二、填空题(每小题5分,共25分)
16.放学后,小明骑车回家,他经过的路程s(千米)与所用时间t(分钟)的函数关系如图所示,则小明的骑车速度是 千米/分钟.
答案:0.2
知识点:函数的图象
解析:解答:由纵坐标看出路程是2千米,
由横坐标看出时间是10分钟,
小明的骑车速度是=0.2(千米/分钟).
分析:根据函数图象的纵坐标,可得路程,根据函数图象的横坐标,可得时间,根据路程与时间的关系,可得答案.
故答案为:0.2
17.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发 小时,快车追上慢车行驶了 千米,快车比慢车早 小时到达B地.
答案:2,276,4
知识点:函数的图象
解析:解答:由图象直接可得出:一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发2小时,快车追上慢车行驶了276千米,快车比慢车早4小时到达B地.
分析:根据横坐标的意义,分别分析得出即可.
故答案为:2,276,4.
18.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t的函数关系的图象如图所示,则休息后园林队绿化面积为 平方米.
答案:100
知识点:函数的图象
解析:解答:由纵坐标看出:休息前绿化面积是60平方米,休息后绿化面积160-60=100平方米.
分析:根据函数图象的纵坐标,即可求得.
故答案为:100.
19.某型号汽油的数量与相应金额的关系如图,那么这种汽油的单价为每升 元.
答案:7.09
知识点:函数的图象
解析:解答:单价=709÷100=7.09元.
分析:根据函数图象知道100升油花费了709元,由此可求出这种汽油的单价.
故答案为:7.09.
20.甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快 千米.
答案:0.4
知识点:函数的图象
解析:解答:根据图示知,甲的速度是:8÷(5-1)=2(千米/小时),
乙的速度是:8÷5=1.6(千米/小时).
则:2-1.6=0.4(千米/小时).
故答案是:0.4.
分析:根据“速度=路程÷时间”分别求甲、乙的速度,然后求其差.
故答案为:7.09元.
三、解答题(每题10分,共50分)
21.小明从家里出发到超市买东西,再回到家,他离家的距离y(千米)与时间t(分钟)的关系如图所示.请你根据图象回答下列问题:
(1)小明家离超市的距离是 千米;
(2)小明在超市买东西时间为 小时;
(3)小明去超市时的速度是 千米/小时.
答案:解答:(1)由纵坐标看出,小明家离超市的距离是3千米;
(2)由横坐标看出到达超市是12,离开超市是72,在超市的时间为72-12=60分钟=1小时;
(3)由纵坐标看出,小明家离超市的距离是3千米,由横坐标看出到达超市是12分钟=0.2小时,小明去超市时的速度是3÷0.2=15千米/小时.
故答案为3,1,15.
知识点:函数的图象
解析:分析:(1)根据函数图象的纵坐标,可得答案;
(2)根据函数图象的横坐标,可得答案;
(3)根据函数图象的纵坐标,可得距离,根据函数的横坐标,可得时间,根据路程与时间的关系,可得答案.
22.一次越野跑中,当李明跑了1600米时,小刚跑了1450米,此后两人匀速跑的路程s(米)与时间t(秒)的关系如图,结合结合图象,求图中S1和S0的位置.
答案:解答:由图象可得出:
(1)小刚比李明早到终点100秒;
(2)两匀速跑时,小刚的速度大于李明的速度;
∵×100-×100=150,
∴S1=2050,
∴S0=1450+×100=1750.
故答案为2050,1750.
知识点:函数的图象
解析:分析:(1)根据图象可得出小刚和李明第一次相遇的时间是100秒;小刚比李明早到终点100秒;两人匀速跑时,小刚的速度大于李明的速度;
(2)求得小刚和李明速度,再乘以相遇时间,两个路程相减即可得出两人的路程之差150.
23.李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下来聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)求a、b、c的值;
(2)求李老师从学校到家的总时间.
答案:解答:由图象可得出:
(1)李老师停留地点离他家的路程为:2000-900=1100(米),
900÷45=20(分).
a=20,b=1100,c=20+30=50;
(2)20+30+1100/110=60(分)
故答案为(1)a=20,b=1100,c=50(2)60分钟.
知识点:函数的图象
解析:分析:(1)根据函数图象和题中给出的信息算出a的值以及b、c的值;
(2)根据等式“时间=路程/速度”分段求出时间,再累加起来算出到家的时间.
24.小强骑自行车去交游,下图表示他离家的距离y(千米)与所用的时间x(小时)之间的函数图象,根据图象所提供的数据,请你写出3个信息.
答案:解答:1.小强从早上9时出发;
2.他在10时30分开始第一次休息;
3.第一次休息11-10.5=0.5小时;
4.小强离家最远为30千米;
5.他在15时回到家等.
知识点:函数的图象
解析:分析:(1)一般应选取最容易得到的答案,比如什么时间出发,到达离家多远的地方;什么时候开始休息,休息了多长时间.
25.某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中所走的路程S(米)与时间t(分)之间的关系.
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;
(2)王老师吃早餐用了多少分钟?
(3)王老师吃早餐以前的速度快还是吃完早餐以后的速度快?吃完早餐后的平均速度是多少?
答案:解答:(1)学校距他家1000米,王老师用25分钟;
(2)王老师吃早餐用了20-10=10分钟;
(3)吃完早餐以后速度快,
(1000-500)÷(25-20)=100(米/分).
知识点:函数的图象
解析:分析:(1)由于步行前往学校,途中在路边一饭店吃早餐,那么行驶路程S(米)与时间t(分)之间的关系图象中有一段平行x轴的线段,然后学校,根据图象可以直接得到结论;(2)根据图象中平行线x轴的线段即可确定王老师吃早餐用了多少时间;
(3)根据图象可以分别求出吃早餐以前的速度和吃完早餐以后的速度,然后比较即可得到结果.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
