河南省许昌市魏都区许昌高级中学2023-2024学年高一下学期开学考试数学试题(含答案)
文档属性
| 名称 | 河南省许昌市魏都区许昌高级中学2023-2024学年高一下学期开学考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 351.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 09:51:35 | ||
图片预览



文档简介
2023-2024学年高一下学期开学检测试题
数学
注意事项:
1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡的相应位置上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
选择题(共8小题,每小题5分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知函数fx=x+4+ln1 x,则f2x的定义域为( )
A. 4,1 B. 4,1 C. 2,12 D. 8,2
2.若α:M=2,4,β:2 M 2,4,5,则α是β的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知a=2log43,b=log48,c=30.6,则( )
A.aC.c4.已知a>b>0>c,则以下不等式不正确的是( )
A.ac2>bc2 B.c+aa>c+bb
C.a2>ab>b2 D.ba>ab
5.“哥德巴赫猜想”是近代三大数学难题之一,其内容是:一个大于2的偶数都可以写成两个素数(质数)之和,也就是我们所谓的“1+1”问题.它是1742年由数学家哥德巴赫提出的,我国数学家潘承洞、王元、陈景润等在哥德巴赫猜想的证明中都取得了相当好的成绩.若将14拆成两个正整数的和,则拆成的和式中,加数全部为素数的概率为( )
A.313 B.513 C.27 D.37
6.已知命题“ x∈R,4x2+(a 2)x+14>0”是假命题,则实数a的取值范围为( )
A. ∞,0∪4,+∞ B.0,4
C.4,+∞ D.0,4
7. 函数的零点所在区间是( )
A. B. C. D.
8.已知,若方程有四个不同的实数根,则的最小值是( )
A. 2 B. 3 C. 4 D.
二.多选题(共4小题,每题5分,共20分。在每题给出的选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分。)
9.下列命题是真命题的是( )
A. 若,则
B. 若非零实数,,满足,,则
C. 若,则
D. 若,,则
10.某学校为了调查学生在一周内生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在区间[50,60)的学生有60人,则下列说法正确的是( )
A.样本中支出在区间[50,60)的频率为0.03
B.样本中支出不少于40元的人数为132
C.n的值为200
D.若该校有2 000名学生,则一定有600人支出在区间[50,60)内
11.下列各对事件中,M,N是相互独立事件的有( )
A.掷1枚质地均匀的骰子一次,事件M=“出现的点数为奇数”,事件N=“出现的点数为偶数”
B.袋中有5个红球,5个黄球,除颜色外完全相同,依次不放回地摸两次,事件M=“第1次摸到红球”,事件N=“第2次摸到红球”
C.分别抛掷2枚相同的硬币,事件M=“第1枚为正面”,事件N=“两枚结果相同”
D.一枚硬币掷两次,事件M=“第一次为正面”,事件N=“第二次为反面”
12.已知函数,则( )
A. 的最小值为2 B. ,
C. D.
三.填空题(共4小题,每题5分,共20分。)
13.若函数与互为反函数,则的单调递减区间是 .
14.若函数f(x)满足f(x+2)=x+3x+2,则f(x)在[1,+∞)上的值域为 .
15. 已知,,且,则的最小值为______.
16.已知函数的值域为,则实数a的取值范围是___________.
四.解答题(共6小题,共70分)
17.设集合A=x∣a+1≤x≤3a,B=x∣5≤x<10.
(1)若a=2,求A∪B, RA∪B;
(2)若A∩B= ,求实数a的取值范围.
18.2022年新冠肺炎仍在世界好多国家肆虐,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨.我市某小区为了防止疫情在小区出现,严防外来人员进入小区,切实保障居民正常生活,设置“特殊值班岗”.现有包含甲、乙在内的4名志愿者参与该工作,每人安排一天,每4天一轮.在一轮的“特殊值班岗”安排中,求:
(1)甲、乙两人相邻值班的概率;
(2)甲或乙被安排在前2天值班的概率.
19.已知.
(1)若的解集A是集合的真子集,求实数a的取值范围;
(2)若对,均有恒成立,求实数a取值范围.
20. 设为数列的前项和,已知为等比数列,且.
(1)求数列的通项公式;
(2)已知,设,记为数列的前项和,证明:.
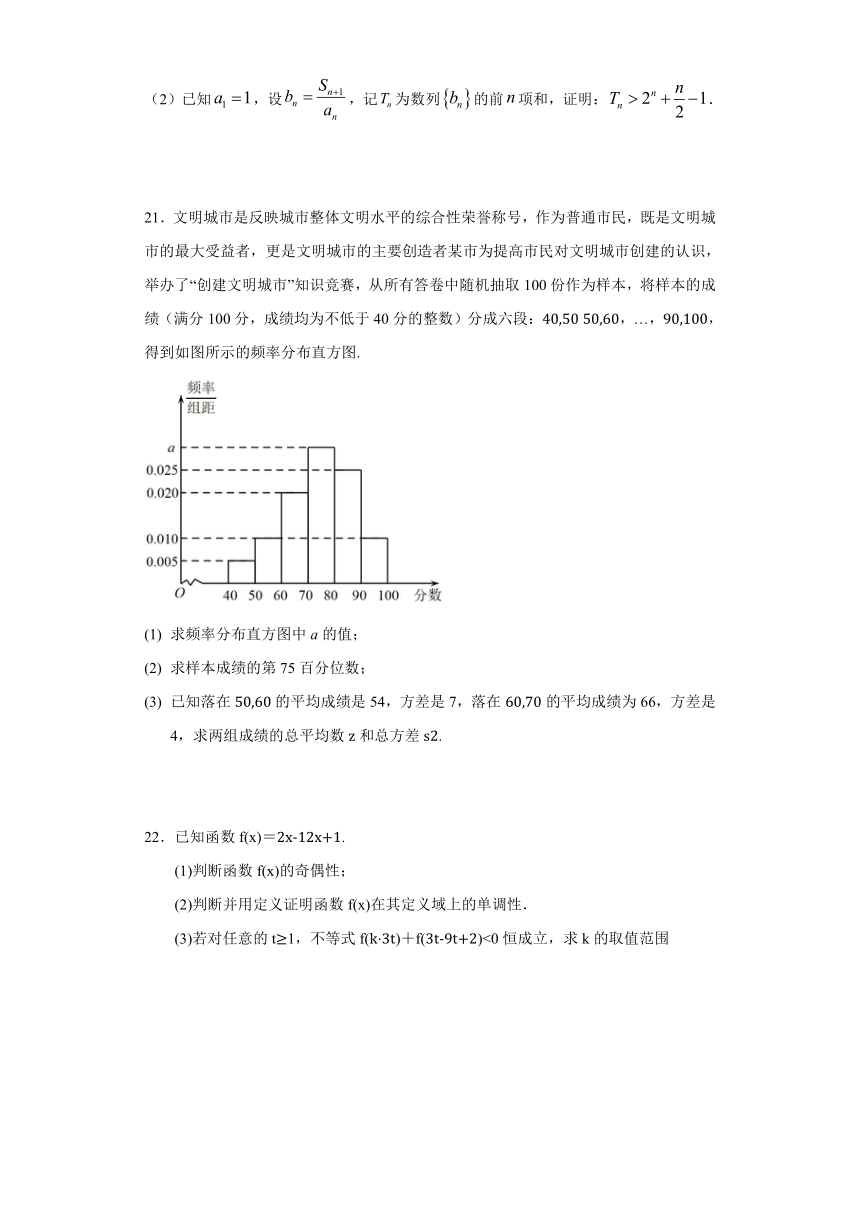
21.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:40,50 50,60,…,90,100,得到如图所示的频率分布直方图.
求频率分布直方图中a的值;
求样本成绩的第75百分位数;
已知落在50,60的平均成绩是54,方差是7,落在60,70的平均成绩为66,方差是4,求两组成绩的总平均数z和总方差s2.
22.已知函数f(x)=2x-12x+1.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t≥1,不等式f(k 3t)+f(3t-9t+2)<0恒成立,求k的取值范围试卷第44页,共44页
数学答案:
1.C 2.A 3.D 4.D 5.A6.A
7.C 8.B解:不妨设,因为方程的根的个数即为与的交点个数,由图象可得:若方程有四个不同的实数根,则,又因为,且,则,可得,又因为,即,可得,所以当时,取到最小值.
9.解:A选项:当时,显然,A错误;
B选项:若非零实数,,满足,,则有,所以,B正确;
C选项:若,则,所以,C正确;
D选项:设,则,解得,
因为,所以,
又,所以,即,D正确.
10.解:样本中支出在区间[50,60)的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;样本中支出不少于40元的人数为0.360.3×60+60=132,故B正确;n=600.3=200,故n的值为200,故C正确;若该校有2 000名学生,则可能有0.3×2 000=600人支出在区间[50,60)内,故D错误.
11.解:在A中,P(MN)=0,所以M,N不相互独立;
在B中,M,N不是相互独立事件;
在C中,P(M)=12,P(N)=12,P(MN)=14,P(MN)=P(M)·P(N),因此M,N是相互独立事件;
在D中,第一次为正面对第二次的结果不影响,因此M,N是相互独立事件.
12.解:,在上单调递减,在上单调递增,
故在上单调递减,在上单调递增,
,函数关于对称,
对选项A:的最小值为,正确;
对选项B:,错误;
对选项C:,故,,正确;
对选项D:,故,错误;
13.. 14.(1,2] 15. 16.
15. 解:因为,,,所以,则,所以,因为
,当且仅当,即时,等号成立,所以.
17.(1)A∪B=x∣3≤x<10, RA∪B=x∣x<3或x≥10 (2) ∞,53∪9,+∞.
【详解】(2)因为A∩B= ,
(i)当A= 时,a+1>3a,解得a<12,此时满足A∩B= ;(ii)当A≠ 时,满足A∩B= ,即需满足a+1≤3a3a<5或a+1≤3aa+1≥10,解得12≤a<53或a≥9.
综上所述,实数a的取值范围为 ∞,53∪9,+∞.
18.(1)12 (2)56【详解】(1)由题意,设4名志愿者为甲,乙,丙,丁,4天一轮的值班安排所有可能的结果是:(甲,乙,丙,丁),……(丁,丙,甲,乙),共24个样本点。设甲乙相邻为事件A,则事件A包含:(甲,乙,丙,丁),……(丁,丙,甲,乙),共12个样本点,故pA=1224=12
(2)设甲或乙被安排在前两天值班的为事件B.则事件B包含:(甲,乙,丙,丁),……(丁,乙,丙,甲),共20个样本点,故pB=2024=56.
19.解:(1)由,可得,
当时,不等式的解集为,
因为集合A是集合的真子集,可得,∴;
当时,不等式的解集为,,满足题意;当时,不等式的解集为,
因为集合A是集合的真子集,可得,∴,
综上所述,实数a的取值范围是
(2)对一切的实数,均有恒成立,即对一切的实数,恒成立,即对一切的实数,恒成立,
即,因为,所以,当且仅当,即时等号成立,所以,故实数a的取值范围是.
20.(1)
(2)证明见解析
(1)由,得,等比数列的首项为1公比为2,可得通项;
(2)由与的关系,求出的通项,通过放缩法证明不等式.
【小问1详解】
为数列的前项和,,
则有,所以,等比数列的公比为2,
又,所以;
【小问2详解】
证明:由(1)知,,当时,,
所以,所以,
则,
因此.
21.(1)a=0.030 (2)84 (3)z=62,s2=37
【详解】(3)解:由图可知,成绩在50,60的市民人数为100×0.1=10,成绩在60,70的市民人数为100×0.2=20,故z=10×54+66×2010+20=62.
设成绩在50,60中10人的分数分别为x1,x2,x3,…,x10;成绩在60,70中20人的分数分别为y1,y2,y3,…,y20,则由题意可得x12+x22+ +x10210 542=7,y12+y22+ +y20220 662=4,
所以x12+x22+ +x102=29230,y12+y22+ +y202=87200,所以s2=110+20x12+x22+ +x102+y12+y22+ +y202 z2=13029230+87200 622=37,所以两组市民成绩的总平均数是62,总方差是37.
22.(3)-∞,43.【详解】(1)∵2x+1≠0,∴函数fx的定义域为R,关于原点对称. ∵f-x=2-x-12-x+1=1-2x1+2x=-2x-12x+1=-fx,∴函数fx为奇函数.
(2)函数fx在定义域上为增函数.证明如下:设x1,x2∈R,且x1(3)∵fk 3t+f3t-9t+2<0,∴fk 3t<-f3t-9t+2.∵函数fx是奇函数,∴fk 3t答案第44页,共44页
答案第33页,共44页
(北京)股份有限公司
数学
注意事项:
1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡的相应位置上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
选择题(共8小题,每小题5分,共40分,每小题给出的四个选项中,只有一项是符合题目要求的。)
1.已知函数fx=x+4+ln1 x,则f2x的定义域为( )
A. 4,1 B. 4,1 C. 2,12 D. 8,2
2.若α:M=2,4,β:2 M 2,4,5,则α是β的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知a=2log43,b=log48,c=30.6,则( )
A.a
A.ac2>bc2 B.c+aa>c+bb
C.a2>ab>b2 D.ba>ab
5.“哥德巴赫猜想”是近代三大数学难题之一,其内容是:一个大于2的偶数都可以写成两个素数(质数)之和,也就是我们所谓的“1+1”问题.它是1742年由数学家哥德巴赫提出的,我国数学家潘承洞、王元、陈景润等在哥德巴赫猜想的证明中都取得了相当好的成绩.若将14拆成两个正整数的和,则拆成的和式中,加数全部为素数的概率为( )
A.313 B.513 C.27 D.37
6.已知命题“ x∈R,4x2+(a 2)x+14>0”是假命题,则实数a的取值范围为( )
A. ∞,0∪4,+∞ B.0,4
C.4,+∞ D.0,4
7. 函数的零点所在区间是( )
A. B. C. D.
8.已知,若方程有四个不同的实数根,则的最小值是( )
A. 2 B. 3 C. 4 D.
二.多选题(共4小题,每题5分,共20分。在每题给出的选项中,有多项符合题目要求。全部选对得5分,部分选对得2分,有选错的得0分。)
9.下列命题是真命题的是( )
A. 若,则
B. 若非零实数,,满足,,则
C. 若,则
D. 若,,则
10.某学校为了调查学生在一周内生活方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如图所示,其中支出在区间[50,60)的学生有60人,则下列说法正确的是( )
A.样本中支出在区间[50,60)的频率为0.03
B.样本中支出不少于40元的人数为132
C.n的值为200
D.若该校有2 000名学生,则一定有600人支出在区间[50,60)内
11.下列各对事件中,M,N是相互独立事件的有( )
A.掷1枚质地均匀的骰子一次,事件M=“出现的点数为奇数”,事件N=“出现的点数为偶数”
B.袋中有5个红球,5个黄球,除颜色外完全相同,依次不放回地摸两次,事件M=“第1次摸到红球”,事件N=“第2次摸到红球”
C.分别抛掷2枚相同的硬币,事件M=“第1枚为正面”,事件N=“两枚结果相同”
D.一枚硬币掷两次,事件M=“第一次为正面”,事件N=“第二次为反面”
12.已知函数,则( )
A. 的最小值为2 B. ,
C. D.
三.填空题(共4小题,每题5分,共20分。)
13.若函数与互为反函数,则的单调递减区间是 .
14.若函数f(x)满足f(x+2)=x+3x+2,则f(x)在[1,+∞)上的值域为 .
15. 已知,,且,则的最小值为______.
16.已知函数的值域为,则实数a的取值范围是___________.
四.解答题(共6小题,共70分)
17.设集合A=x∣a+1≤x≤3a,B=x∣5≤x<10.
(1)若a=2,求A∪B, RA∪B;
(2)若A∩B= ,求实数a的取值范围.
18.2022年新冠肺炎仍在世界好多国家肆虐,尽管我国抗疫取得了很大的成绩,疫情也得到了很好的遏制,但由于整个国际环境的影响,时而也会出现一些散发病例,故而抗疫形势依然艰巨.我市某小区为了防止疫情在小区出现,严防外来人员进入小区,切实保障居民正常生活,设置“特殊值班岗”.现有包含甲、乙在内的4名志愿者参与该工作,每人安排一天,每4天一轮.在一轮的“特殊值班岗”安排中,求:
(1)甲、乙两人相邻值班的概率;
(2)甲或乙被安排在前2天值班的概率.
19.已知.
(1)若的解集A是集合的真子集,求实数a的取值范围;
(2)若对,均有恒成立,求实数a取值范围.
20. 设为数列的前项和,已知为等比数列,且.
(1)求数列的通项公式;
(2)已知,设,记为数列的前项和,证明:.
21.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:40,50 50,60,…,90,100,得到如图所示的频率分布直方图.
求频率分布直方图中a的值;
求样本成绩的第75百分位数;
已知落在50,60的平均成绩是54,方差是7,落在60,70的平均成绩为66,方差是4,求两组成绩的总平均数z和总方差s2.
22.已知函数f(x)=2x-12x+1.
(1)判断函数f(x)的奇偶性;
(2)判断并用定义证明函数f(x)在其定义域上的单调性.
(3)若对任意的t≥1,不等式f(k 3t)+f(3t-9t+2)<0恒成立,求k的取值范围试卷第44页,共44页
数学答案:
1.C 2.A 3.D 4.D 5.A6.A
7.C 8.B解:不妨设,因为方程的根的个数即为与的交点个数,由图象可得:若方程有四个不同的实数根,则,又因为,且,则,可得,又因为,即,可得,所以当时,取到最小值.
9.解:A选项:当时,显然,A错误;
B选项:若非零实数,,满足,,则有,所以,B正确;
C选项:若,则,所以,C正确;
D选项:设,则,解得,
因为,所以,
又,所以,即,D正确.
10.解:样本中支出在区间[50,60)的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;样本中支出不少于40元的人数为0.360.3×60+60=132,故B正确;n=600.3=200,故n的值为200,故C正确;若该校有2 000名学生,则可能有0.3×2 000=600人支出在区间[50,60)内,故D错误.
11.解:在A中,P(MN)=0,所以M,N不相互独立;
在B中,M,N不是相互独立事件;
在C中,P(M)=12,P(N)=12,P(MN)=14,P(MN)=P(M)·P(N),因此M,N是相互独立事件;
在D中,第一次为正面对第二次的结果不影响,因此M,N是相互独立事件.
12.解:,在上单调递减,在上单调递增,
故在上单调递减,在上单调递增,
,函数关于对称,
对选项A:的最小值为,正确;
对选项B:,错误;
对选项C:,故,,正确;
对选项D:,故,错误;
13.. 14.(1,2] 15. 16.
15. 解:因为,,,所以,则,所以,因为
,当且仅当,即时,等号成立,所以.
17.(1)A∪B=x∣3≤x<10, RA∪B=x∣x<3或x≥10 (2) ∞,53∪9,+∞.
【详解】(2)因为A∩B= ,
(i)当A= 时,a+1>3a,解得a<12,此时满足A∩B= ;(ii)当A≠ 时,满足A∩B= ,即需满足a+1≤3a3a<5或a+1≤3aa+1≥10,解得12≤a<53或a≥9.
综上所述,实数a的取值范围为 ∞,53∪9,+∞.
18.(1)12 (2)56【详解】(1)由题意,设4名志愿者为甲,乙,丙,丁,4天一轮的值班安排所有可能的结果是:(甲,乙,丙,丁),……(丁,丙,甲,乙),共24个样本点。设甲乙相邻为事件A,则事件A包含:(甲,乙,丙,丁),……(丁,丙,甲,乙),共12个样本点,故pA=1224=12
(2)设甲或乙被安排在前两天值班的为事件B.则事件B包含:(甲,乙,丙,丁),……(丁,乙,丙,甲),共20个样本点,故pB=2024=56.
19.解:(1)由,可得,
当时,不等式的解集为,
因为集合A是集合的真子集,可得,∴;
当时,不等式的解集为,,满足题意;当时,不等式的解集为,
因为集合A是集合的真子集,可得,∴,
综上所述,实数a的取值范围是
(2)对一切的实数,均有恒成立,即对一切的实数,恒成立,即对一切的实数,恒成立,
即,因为,所以,当且仅当,即时等号成立,所以,故实数a的取值范围是.
20.(1)
(2)证明见解析
(1)由,得,等比数列的首项为1公比为2,可得通项;
(2)由与的关系,求出的通项,通过放缩法证明不等式.
【小问1详解】
为数列的前项和,,
则有,所以,等比数列的公比为2,
又,所以;
【小问2详解】
证明:由(1)知,,当时,,
所以,所以,
则,
因此.
21.(1)a=0.030 (2)84 (3)z=62,s2=37
【详解】(3)解:由图可知,成绩在50,60的市民人数为100×0.1=10,成绩在60,70的市民人数为100×0.2=20,故z=10×54+66×2010+20=62.
设成绩在50,60中10人的分数分别为x1,x2,x3,…,x10;成绩在60,70中20人的分数分别为y1,y2,y3,…,y20,则由题意可得x12+x22+ +x10210 542=7,y12+y22+ +y20220 662=4,
所以x12+x22+ +x102=29230,y12+y22+ +y202=87200,所以s2=110+20x12+x22+ +x102+y12+y22+ +y202 z2=13029230+87200 622=37,所以两组市民成绩的总平均数是62,总方差是37.
22.(3)-∞,43.【详解】(1)∵2x+1≠0,∴函数fx的定义域为R,关于原点对称. ∵f-x=2-x-12-x+1=1-2x1+2x=-2x-12x+1=-fx,∴函数fx为奇函数.
(2)函数fx在定义域上为增函数.证明如下:设x1,x2∈R,且x1
答案第33页,共44页
(北京)股份有限公司
同课章节目录
