人教版5下数学2.2《2、5、3的倍数的特征》同步练习(含答案)
文档属性
| 名称 | 人教版5下数学2.2《2、5、3的倍数的特征》同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 157.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2.2《2、5、3的倍数的特征》同步练习
班级:_________ 姓名:__________
一、选择题
1.某市《开学第一课》在各大网络平台点击量高达百万次,皮皮和爸爸妈妈一起观看,他们点击的次数恰好是3的倍数,又是2的倍数,他们可以是第( )次点击观看。
A.2057 B.1224 C.3364
2.食品店运来77个面包,下面哪种装法可以正好装完( )。
A.7个装一袋 B.5个装一袋 C.2个装一袋
3.51□是一个三位数,要使它既是2的倍数,也有因数3,□里可以填( )。
A.2 B.3 C.6
4.同时是2、3、5倍数的最小三位数是( )。
A.100 B.102 C.120 D.130
5.5个连续的偶数,中间的一个数为m,其中最小的数是( )。
A.m-2 B.m-3 C.m-4
6.在下边的百数表中,用去盖,那盖住的5个数之和不可能是( )。
A.195 B.130 C.236 D.335
二、填空题
7.甲乙丙是三个连续的偶数,甲数最小。如果乙数是a,那么甲数是( ),丙数是( )。
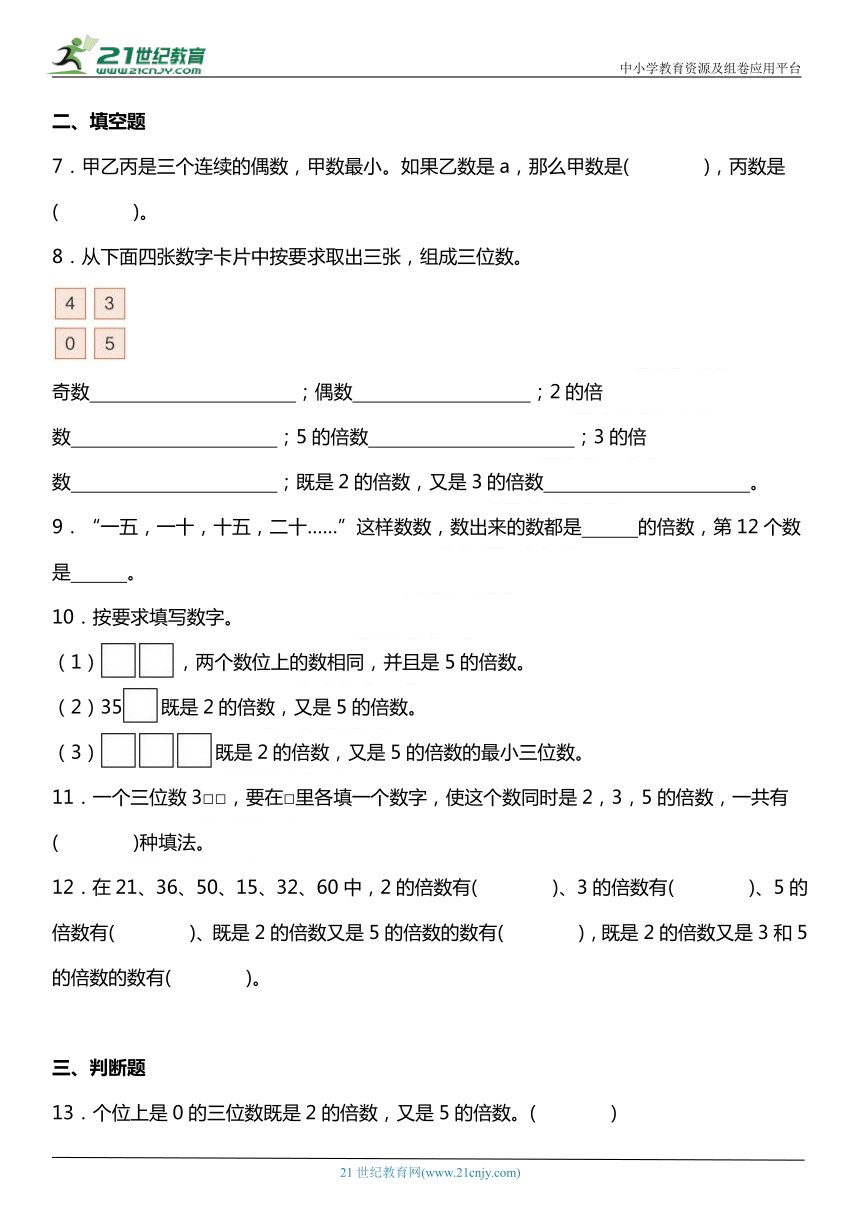
8.从下面四张数字卡片中按要求取出三张,组成三位数。
奇数 ;偶数 ;2的倍数 ;5的倍数 ;3的倍数 ;既是2的倍数,又是3的倍数 。
9.“一五,一十,十五,二十……”这样数数,数出来的数都是 的倍数,第12个数是 。
10.按要求填写数字。
(1),两个数位上的数相同,并且是5的倍数。
(2)35既是2的倍数,又是5的倍数。
(3)既是2的倍数,又是5的倍数的最小三位数。
11.一个三位数3□□,要在□里各填一个数字,使这个数同时是2,3,5的倍数,一共有( )种填法。
12.在21、36、50、15、32、60中,2的倍数有( )、3的倍数有( )、5的倍数有( )、既是2的倍数又是5的倍数的数有( ),既是2的倍数又是3和5的倍数的数有( )。
三、判断题
13.个位上是0的三位数既是2的倍数,又是5的倍数。( )
14.M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。( )
15.a表示自然数,那么,2a-1一定是奇数。( )
16.如果a是奇数,那么1097+89+a+25的结果还是奇数。( )
17.一个三位数的末尾是0,这个三位数既是偶数,又是2和5的倍数。( )
18.个位上的数字是3的倍数的数一定不是3的倍数。( )
四、解答题
19.下面哪些数是2的倍数?哪些数是5的倍数?哪些数既是2的倍数,又是5的倍数?你发现了什么?
35 67 99 106 60 75 130 521 280 6018
20.奇数与奇数的积是奇数还是偶数?奇数与偶数的积是奇数还是偶数?偶数与偶数的积呢?
21.(1)判断一个数是不是2或5的倍数,为什么只用看个位数?
一个数可以根据数的组成进行改写,比如:
其中10,100,1000都是2或5的倍数,所以只要个位上的数是2或5的倍数,这个数就是2或5的倍数。
(2)判断一个数是不是3的倍数,为什么要看各位上数的和?
可以按(1)的思路进行分析。
其中9,99,999都是3的倍数,括号中是这个数各个数位上的数,所以只要这些数的和是3的倍数,这个数就是3的倍数。
试一试:你能继续找到判断9的倍数的方法吗?
22.先圈出4的倍数,再回答下面的问题。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
(1)4的倍数都是2的倍数吗?
(2)只看个位,能否判断一个数是不是4的倍数?应该怎样判断?
23.判断下面的说法是否正确,并说一说你的理由。
(1)个位上是3,6,9的数,都是3的倍数。
(2)个位上是1,3,5,7,9的数,都是奇数。
(3)在全部整数里,不是奇数就是偶数。
参考答案:
1.B
【分析】既是2的倍数,又是3的倍数的数的特征:个位上是0、2、4、6、8;各个数位上的数字的和是3的倍数。据此解答。
【详解】A.2057的个位上是7,则它不是2的倍数,不符合题意;
B.1224的个位上是4,则它是2的倍数,且1+2+2+4=9,9是3的倍数,所以1224既是2的倍数,又是3的倍数,符合题意;
C.3364的个位上是4,它是2的倍数,但是3+3+6+4=16,16不是3的倍数,则3364不是3的倍数,不符合题意。
故答案为:B
2.A
【分析】想正好装完,77应该是每袋里面面包个数的倍数,验证各选项的倍数是不是77即可。
【详解】A.77÷7=11(袋),77是7的倍数,可以正好装完;
B.个位是0或5的数是5的倍数,77不是5的倍数,无法正好装完;
C.个位是0、2、4、6、8的数是2的倍数,77不是2的倍数,无法正好装完。
故答案为:A
3.C
【分析】既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
【详解】51□是一个三位数,要使它既是2的倍数,个位数可以填0、2、4、6、8,5+1=6、6有因数3,个位可以填0、3、6、9,要使它既是2的倍数,也有因数3,□里可以填0或6。
故答案为:C
4.C
【分析】2的倍数的特征:个位上是 0、2、4、6、8的数,都是2的倍数;3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数;5的倍数的特征:个位上是0或5的数,都是5的倍数。这个数同时是2、3、5的倍数,则这个三位数是2×3×5=30的倍数。
【详解】由分析可知:2×3×5=30,则这个数是30的倍数,因此符合条件的最小的三位数是120。
故答案为:C
5.C
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
连续偶数的特点:两个相邻的偶数相差2。
已知5个连续偶数的中间一个数为m,根据连续偶数的特点,分别写出其他4个偶数,找出最小的数即可。
【详解】5个连续的偶数,中间的一个数为m,根据连续偶数的特点,这5个连续的偶数分别是:
m-4,m-2,m,m+2,m+4;
其中最小的数是m-4。
故答案为:C
6.C
【分析】百数表中每一行有10个数字,用去盖,则可设中间的数为未知数,左右两边分别是未知数减一,未知数加一,上下两个数分别为未知数减10、未知数加10;则5个数相加得到5的倍数,再进行解答。
【详解】可设中间的数为x,则左右两侧的数分别为:x-1、x+1,上下两个数分别为:x-10、x+10,则5个数的和为:
即5个数之和是5的倍数,根据5的倍数特征:是5的倍数的整数个位上是0或5,四个选项中236的个位商的数不是0或5。
故答案为:C
【点睛】
7. a-2 a+2/2+a
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
连续偶数的特点:两个相邻的偶数相差2。
已知甲乙丙三个连续的偶数中,乙数是a,即三个连续偶数中间的偶数是a,那么用中间的偶数分别减2、加2,即可求出相邻的另外两个偶数。
【详解】甲乙丙是三个连续的偶数,甲数最小。如果乙数是a,那么甲数是a-2,丙数是a+2。
8. 435、405、403、453、345、305、543、503 430、450、340、304、350、354、540、530、534、504 430、450、340、304、350、354、540、530、534、504 430、435、405、450、340、345、305、350、540、530 435、405、450、453、345、354、543、540、534、504 450、354、540、534、504
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。
5的倍数特征:个位上的数字是0或5的数是5的倍数。
3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数;据此解答。
【详解】用4、3、0、5中的三个数组成的三位数有:430、435、405、403、450、453、340、345、305、304、350、354、543、540、530、534、503、504;
所以组成的三位数是奇数的数有:435、405、403、453、345、305、543、503;
是偶数的数有:430、450、340、304、350、354、540、530、534、504;
2的倍数有:430、450、340、304、350、354、540、530、534、504;
5的倍数有:430、435、405、450、340、345、305、350、540、530;
3的倍数有: 435、405、450、453、345、354、543、540、534、504;
既是2的倍数,又是3的倍数有:450、354、540、534、504。
9. 5 60
【分析】5的最小倍数是5,“一五,一十,十五,二十……”这样数数,相当于从5开始数数,依次加5,数出来的数都是5的倍数;第12个数就是5个5个的依次数12次,用5×12即可。。
【详解】5×12=60
“一五,一十,十五,二十……”这样数数,数出来的数都是5的倍数,第12个数是60。
10.(1)55
(2)350
(3)100
【分析】(1)5的倍数特征:个位上的数字是0或5的数是5的倍数。
(2)(3)既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。
【详解】(1)55,两个数位上的数相同,并且是5的倍数。
(2)350既是2的倍数,又是5的倍数。
(3)100既是2的倍数,又是5的倍数的最小三位数。
11.4
【分析】2的倍数的特征是,个位数字是0,2,4,6,8;3的倍数的特征是,各位数字之和能被3整除;5的倍数的特征是,个位数字是0或5,要使这个三位数同时是2,5、3的倍数,必须满足这三个条件,百位是3,个位是0,再找出十位上的数,即可解答。
【详解】个位上的□是0;
十位上的□:
如果是0;3+0+0=3;3能被3整数;可以填0;
如果是1;3+1+0=4;4不能被3整除;不能填1;
如果是2;3+2+0=5;5不能被3整数;不能填2;
如果是3;3+3+0=6;6能被3整数,可以填3;
如果是4;3+4+0=7;7不能被3整数,不能填4;
如果是5;3+5+0=8;8不能被3整数,不能填5;
如果是6;3+6+0=9;9能被3整数,可以填6;
如果是7;3+7+0=10;10不能被3整数,不能填7;
如果是8;3+8+0=11;11不能被3整数,不能填8;
如果是9;3+9+0=12;12能被3整数,可以填9。
一共有4种填法。
一个三位数3□□,要在□里各填一个数字,使这个数同时是2,3,5的倍数,一共有4种填法。
12. 36、50、32、60 21、36、15、60 50、15、60 50、60 60
【分析】2的倍数特征:末尾数字是0、2、4、6、8的数是2的倍数;3的倍数特征:各个数位上的数字之和是3的倍数,这个数字就是3的倍数;5的倍数特征:末尾数字是0或5的数是5的倍数;一个数既是2的倍数又是5的倍数,则这个数的个位数字一定是0。据此解答即可。
【详解】在21、36、50、15、32、60中,2的倍数有36、50、32、60、3的倍数有21、36、15、60、5的倍数有50、15、60、既是2的倍数又是5的倍数的数有50、60,既是2的倍数又是3和5的倍数的数有60。
13.√
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。据此解答。
【详解】根据2的倍数、5的倍数特征可知,如果一个数既是2的倍数,又是5的倍数,那么这个数的个位一定是0。
所以,个位上是0的三位数既是2的倍数,又是5的倍数。
原题说法正确。
故答案为:√
14.√
【分析】因为M÷N=5,则M÷5=N,M和N都是非零自然数,所以M是5的倍数;再根据5的倍数特征:个位上的数字是0或5的数是5的倍数,所以M的个位上是0或5,据此解答。
【详解】根据分析可知,M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。
故答案为:√
15.×
【分析】a是非0自然数,那么2a是偶数,则2a-1是奇数。据此解答即可。
【详解】由分析可得:题干中没有表示a是非0自然数,只有当a是非0自然数,那么2a是偶数,则2a-1是奇数,所以原题说法错误。
故答案为:×
16.×
【分析】奇数是指不能被2整除的整数,根据奇数加法的性质判定,偶数个的奇数相加,得到的结果是偶数。据此可得出答案。
【详解】1097+89+a+25式子中,1097、89、25都是奇数,如果a是奇数,则是4个奇数相加,是偶数个,则得到的结果是偶数。原题说法错误。
故答案为:×
17.√
【分析】个位是0、2、4、6、8的数是2的倍数;个位上是0或5的数是5的倍数;既是2又是5的倍数的特征是个位是0;是2的倍数的数叫做偶数。据此判断。
【详解】由分析可知,一个三位数的末尾是0,这个三位数既是偶数,又是2和5的倍数。如,100是偶数,也是2和5的倍数。所以,原说法正确。
故答案为:√
18.×
【分析】根据3的倍数的特征,各个数位上的数字之和是3的倍数,这个数就是3的倍数,据此举例判断即可。
【详解】如23个位上是3的数,但23不是3的倍数;33个位上是3的数,但33是3的倍数。所以个位上是3的数一定不是3的倍数说法错误。
故答案为:×
【点睛】本题考查3的倍数,明确3的倍数特征是解题的关键。
19.见详解
【分析】2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。
5的倍数特征:个位上的数字是0或5的数是5的倍数。
既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。
【详解】2的倍数有:106;60;130;280;6018
5的倍数有:35、60、75、130、280
2的倍数又是5的倍数有:60、130、280
发现:既是2的倍数又是5的倍数的末尾一定是0。
20.奇数;偶数;偶数
【分析】在自然数中,是2的倍数的数叫做偶数;不是2的倍数的数叫做奇数。据此解答。
【详解】奇数与奇数的积是奇数,比如3×5=15;
奇数与偶数的积是偶数,比如3×4=12;
偶数与偶数的积是偶数,比如2×4=8。
21.见详解
【分析】题干(1)中给出的方法,是根据数的组成进行改写,看这个数分别是由几个千、几个百、几个十和几个一组成,因为10,100,1000都是2或5的倍数,整十整百整千数无论乘几得到的数都是2或5的倍数,因此所以只要个位上的数是2或5的倍数,这个数就是2或5的倍数。
根据(1)的思路分析3的倍数的特征,利用乘法分配律,得到999、99、9分别乘一个数,因为999、99、9都是3的倍数,因此999、99、9无论乘几得到的数都是3的倍数,而余下的数相加刚好是各个数位上的数之和,因此只要一个数的各数位上的数字之和是3的倍数,这个数就是3的倍数。
根据这个思路,先写出一个9的倍数,将这个数根据数的组成进行改写,利用乘法分配律进行转化,可以得出与3的倍数的特征类似的9的倍数的特征。
【详解】9×181=1629
1629是9的倍数。
1629=1×1000+6×100+2×10+9×1
=1×(999+1)+6×(99+1)+2×(9+1)+9
=1×999+6×999+2×9+(1+6+2+9)
其中9,99,999都是9的倍数,括号中是这个数各个数位上的数,所以只要这些数的和是9的倍数,这个数就是9的倍数。
22.
见详解
【分析】(1)个位上是0,2,4,6或8的数,都是2的倍数。观察圈出来的数,则4的倍数都能被2整除。
(2)对圈出来的数观察发现,个位没有规律。所以只看个位不能判断一个数是不是4的倍数。一个整数的末尾两位数能被4整除,则这个数是4的倍数。
【详解】
(1)观察发现,圈出的4的倍数是2的倍数。
(2)只看个位,没有特别的规律。所以只看个位,不能判断一个数是不是4的倍数。
23.(1)×,13个位上的数是3,但不是3的倍数。
(2)√,11,23,35,47,59都是奇数。
(3)√,整数可以分为奇数和偶数,0是特殊的偶数。
【分析】(1)一个数各位上的数的和是3的倍数,这个数就是3的倍数。
(2)不是2的倍数的是奇数。
(3)一个整数不是奇数就是偶数。0是比较特殊的,但是能被2整除,所以0也是偶数。
【详解】(1)13个位上的数是3,但不是3的倍数。所以个位上是3,6,9的数,都是3的倍数说法错误。
(2)11,23,35,47,59都是奇数。所以个位上是1,3,5,7,9的数,都是奇数说法正确。
(3)整数可以分为奇数和偶数,0是特殊的偶数。所以在全部整数里,不是奇数就是偶数说法正确。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.2《2、5、3的倍数的特征》同步练习
班级:_________ 姓名:__________
一、选择题
1.某市《开学第一课》在各大网络平台点击量高达百万次,皮皮和爸爸妈妈一起观看,他们点击的次数恰好是3的倍数,又是2的倍数,他们可以是第( )次点击观看。
A.2057 B.1224 C.3364
2.食品店运来77个面包,下面哪种装法可以正好装完( )。
A.7个装一袋 B.5个装一袋 C.2个装一袋
3.51□是一个三位数,要使它既是2的倍数,也有因数3,□里可以填( )。
A.2 B.3 C.6
4.同时是2、3、5倍数的最小三位数是( )。
A.100 B.102 C.120 D.130
5.5个连续的偶数,中间的一个数为m,其中最小的数是( )。
A.m-2 B.m-3 C.m-4
6.在下边的百数表中,用去盖,那盖住的5个数之和不可能是( )。
A.195 B.130 C.236 D.335
二、填空题
7.甲乙丙是三个连续的偶数,甲数最小。如果乙数是a,那么甲数是( ),丙数是( )。
8.从下面四张数字卡片中按要求取出三张,组成三位数。
奇数 ;偶数 ;2的倍数 ;5的倍数 ;3的倍数 ;既是2的倍数,又是3的倍数 。
9.“一五,一十,十五,二十……”这样数数,数出来的数都是 的倍数,第12个数是 。
10.按要求填写数字。
(1),两个数位上的数相同,并且是5的倍数。
(2)35既是2的倍数,又是5的倍数。
(3)既是2的倍数,又是5的倍数的最小三位数。
11.一个三位数3□□,要在□里各填一个数字,使这个数同时是2,3,5的倍数,一共有( )种填法。
12.在21、36、50、15、32、60中,2的倍数有( )、3的倍数有( )、5的倍数有( )、既是2的倍数又是5的倍数的数有( ),既是2的倍数又是3和5的倍数的数有( )。
三、判断题
13.个位上是0的三位数既是2的倍数,又是5的倍数。( )
14.M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。( )
15.a表示自然数,那么,2a-1一定是奇数。( )
16.如果a是奇数,那么1097+89+a+25的结果还是奇数。( )
17.一个三位数的末尾是0,这个三位数既是偶数,又是2和5的倍数。( )
18.个位上的数字是3的倍数的数一定不是3的倍数。( )
四、解答题
19.下面哪些数是2的倍数?哪些数是5的倍数?哪些数既是2的倍数,又是5的倍数?你发现了什么?
35 67 99 106 60 75 130 521 280 6018
20.奇数与奇数的积是奇数还是偶数?奇数与偶数的积是奇数还是偶数?偶数与偶数的积呢?
21.(1)判断一个数是不是2或5的倍数,为什么只用看个位数?
一个数可以根据数的组成进行改写,比如:
其中10,100,1000都是2或5的倍数,所以只要个位上的数是2或5的倍数,这个数就是2或5的倍数。
(2)判断一个数是不是3的倍数,为什么要看各位上数的和?
可以按(1)的思路进行分析。
其中9,99,999都是3的倍数,括号中是这个数各个数位上的数,所以只要这些数的和是3的倍数,这个数就是3的倍数。
试一试:你能继续找到判断9的倍数的方法吗?
22.先圈出4的倍数,再回答下面的问题。
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
(1)4的倍数都是2的倍数吗?
(2)只看个位,能否判断一个数是不是4的倍数?应该怎样判断?
23.判断下面的说法是否正确,并说一说你的理由。
(1)个位上是3,6,9的数,都是3的倍数。
(2)个位上是1,3,5,7,9的数,都是奇数。
(3)在全部整数里,不是奇数就是偶数。
参考答案:
1.B
【分析】既是2的倍数,又是3的倍数的数的特征:个位上是0、2、4、6、8;各个数位上的数字的和是3的倍数。据此解答。
【详解】A.2057的个位上是7,则它不是2的倍数,不符合题意;
B.1224的个位上是4,则它是2的倍数,且1+2+2+4=9,9是3的倍数,所以1224既是2的倍数,又是3的倍数,符合题意;
C.3364的个位上是4,它是2的倍数,但是3+3+6+4=16,16不是3的倍数,则3364不是3的倍数,不符合题意。
故答案为:B
2.A
【分析】想正好装完,77应该是每袋里面面包个数的倍数,验证各选项的倍数是不是77即可。
【详解】A.77÷7=11(袋),77是7的倍数,可以正好装完;
B.个位是0或5的数是5的倍数,77不是5的倍数,无法正好装完;
C.个位是0、2、4、6、8的数是2的倍数,77不是2的倍数,无法正好装完。
故答案为:A
3.C
【分析】既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数。
【详解】51□是一个三位数,要使它既是2的倍数,个位数可以填0、2、4、6、8,5+1=6、6有因数3,个位可以填0、3、6、9,要使它既是2的倍数,也有因数3,□里可以填0或6。
故答案为:C
4.C
【分析】2的倍数的特征:个位上是 0、2、4、6、8的数,都是2的倍数;3的倍数的特征:一个数各位上的数的和是3的倍数,这个数就是3的倍数;5的倍数的特征:个位上是0或5的数,都是5的倍数。这个数同时是2、3、5的倍数,则这个三位数是2×3×5=30的倍数。
【详解】由分析可知:2×3×5=30,则这个数是30的倍数,因此符合条件的最小的三位数是120。
故答案为:C
5.C
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
连续偶数的特点:两个相邻的偶数相差2。
已知5个连续偶数的中间一个数为m,根据连续偶数的特点,分别写出其他4个偶数,找出最小的数即可。
【详解】5个连续的偶数,中间的一个数为m,根据连续偶数的特点,这5个连续的偶数分别是:
m-4,m-2,m,m+2,m+4;
其中最小的数是m-4。
故答案为:C
6.C
【分析】百数表中每一行有10个数字,用去盖,则可设中间的数为未知数,左右两边分别是未知数减一,未知数加一,上下两个数分别为未知数减10、未知数加10;则5个数相加得到5的倍数,再进行解答。
【详解】可设中间的数为x,则左右两侧的数分别为:x-1、x+1,上下两个数分别为:x-10、x+10,则5个数的和为:
即5个数之和是5的倍数,根据5的倍数特征:是5的倍数的整数个位上是0或5,四个选项中236的个位商的数不是0或5。
故答案为:C
【点睛】
7. a-2 a+2/2+a
【分析】整数中,是2的倍数的数叫做偶数,不是2的倍数的数叫做奇数。
连续偶数的特点:两个相邻的偶数相差2。
已知甲乙丙三个连续的偶数中,乙数是a,即三个连续偶数中间的偶数是a,那么用中间的偶数分别减2、加2,即可求出相邻的另外两个偶数。
【详解】甲乙丙是三个连续的偶数,甲数最小。如果乙数是a,那么甲数是a-2,丙数是a+2。
8. 435、405、403、453、345、305、543、503 430、450、340、304、350、354、540、530、534、504 430、450、340、304、350、354、540、530、534、504 430、435、405、450、340、345、305、350、540、530 435、405、450、453、345、354、543、540、534、504 450、354、540、534、504
【分析】整数中,是2的倍数的数叫偶数,不是2的倍数的数叫奇数。
2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。
5的倍数特征:个位上的数字是0或5的数是5的倍数。
3的倍数的特征:一个数各个数位上的数字的和是3的倍数,这个数就是3的倍数。
既是2的倍数又是3的倍数的特征:个位上的数字是0、2、4、6、8,各个数位上的数字的和是3的倍数的数;据此解答。
【详解】用4、3、0、5中的三个数组成的三位数有:430、435、405、403、450、453、340、345、305、304、350、354、543、540、530、534、503、504;
所以组成的三位数是奇数的数有:435、405、403、453、345、305、543、503;
是偶数的数有:430、450、340、304、350、354、540、530、534、504;
2的倍数有:430、450、340、304、350、354、540、530、534、504;
5的倍数有:430、435、405、450、340、345、305、350、540、530;
3的倍数有: 435、405、450、453、345、354、543、540、534、504;
既是2的倍数,又是3的倍数有:450、354、540、534、504。
9. 5 60
【分析】5的最小倍数是5,“一五,一十,十五,二十……”这样数数,相当于从5开始数数,依次加5,数出来的数都是5的倍数;第12个数就是5个5个的依次数12次,用5×12即可。。
【详解】5×12=60
“一五,一十,十五,二十……”这样数数,数出来的数都是5的倍数,第12个数是60。
10.(1)55
(2)350
(3)100
【分析】(1)5的倍数特征:个位上的数字是0或5的数是5的倍数。
(2)(3)既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。
【详解】(1)55,两个数位上的数相同,并且是5的倍数。
(2)350既是2的倍数,又是5的倍数。
(3)100既是2的倍数,又是5的倍数的最小三位数。
11.4
【分析】2的倍数的特征是,个位数字是0,2,4,6,8;3的倍数的特征是,各位数字之和能被3整除;5的倍数的特征是,个位数字是0或5,要使这个三位数同时是2,5、3的倍数,必须满足这三个条件,百位是3,个位是0,再找出十位上的数,即可解答。
【详解】个位上的□是0;
十位上的□:
如果是0;3+0+0=3;3能被3整数;可以填0;
如果是1;3+1+0=4;4不能被3整除;不能填1;
如果是2;3+2+0=5;5不能被3整数;不能填2;
如果是3;3+3+0=6;6能被3整数,可以填3;
如果是4;3+4+0=7;7不能被3整数,不能填4;
如果是5;3+5+0=8;8不能被3整数,不能填5;
如果是6;3+6+0=9;9能被3整数,可以填6;
如果是7;3+7+0=10;10不能被3整数,不能填7;
如果是8;3+8+0=11;11不能被3整数,不能填8;
如果是9;3+9+0=12;12能被3整数,可以填9。
一共有4种填法。
一个三位数3□□,要在□里各填一个数字,使这个数同时是2,3,5的倍数,一共有4种填法。
12. 36、50、32、60 21、36、15、60 50、15、60 50、60 60
【分析】2的倍数特征:末尾数字是0、2、4、6、8的数是2的倍数;3的倍数特征:各个数位上的数字之和是3的倍数,这个数字就是3的倍数;5的倍数特征:末尾数字是0或5的数是5的倍数;一个数既是2的倍数又是5的倍数,则这个数的个位数字一定是0。据此解答即可。
【详解】在21、36、50、15、32、60中,2的倍数有36、50、32、60、3的倍数有21、36、15、60、5的倍数有50、15、60、既是2的倍数又是5的倍数的数有50、60,既是2的倍数又是3和5的倍数的数有60。
13.√
【分析】2的倍数特征:个位上是0、2、4、6、8的数。
5的倍数特征:个位上是0或5的数。据此解答。
【详解】根据2的倍数、5的倍数特征可知,如果一个数既是2的倍数,又是5的倍数,那么这个数的个位一定是0。
所以,个位上是0的三位数既是2的倍数,又是5的倍数。
原题说法正确。
故答案为:√
14.√
【分析】因为M÷N=5,则M÷5=N,M和N都是非零自然数,所以M是5的倍数;再根据5的倍数特征:个位上的数字是0或5的数是5的倍数,所以M的个位上是0或5,据此解答。
【详解】根据分析可知,M和N都是非零自然数,且M÷N=5,那么M的个位上是0或5。
故答案为:√
15.×
【分析】a是非0自然数,那么2a是偶数,则2a-1是奇数。据此解答即可。
【详解】由分析可得:题干中没有表示a是非0自然数,只有当a是非0自然数,那么2a是偶数,则2a-1是奇数,所以原题说法错误。
故答案为:×
16.×
【分析】奇数是指不能被2整除的整数,根据奇数加法的性质判定,偶数个的奇数相加,得到的结果是偶数。据此可得出答案。
【详解】1097+89+a+25式子中,1097、89、25都是奇数,如果a是奇数,则是4个奇数相加,是偶数个,则得到的结果是偶数。原题说法错误。
故答案为:×
17.√
【分析】个位是0、2、4、6、8的数是2的倍数;个位上是0或5的数是5的倍数;既是2又是5的倍数的特征是个位是0;是2的倍数的数叫做偶数。据此判断。
【详解】由分析可知,一个三位数的末尾是0,这个三位数既是偶数,又是2和5的倍数。如,100是偶数,也是2和5的倍数。所以,原说法正确。
故答案为:√
18.×
【分析】根据3的倍数的特征,各个数位上的数字之和是3的倍数,这个数就是3的倍数,据此举例判断即可。
【详解】如23个位上是3的数,但23不是3的倍数;33个位上是3的数,但33是3的倍数。所以个位上是3的数一定不是3的倍数说法错误。
故答案为:×
【点睛】本题考查3的倍数,明确3的倍数特征是解题的关键。
19.见详解
【分析】2的倍数特征:个位上的数字是0、2、4、6、8的数是2的倍数。
5的倍数特征:个位上的数字是0或5的数是5的倍数。
既是2的倍数又是5的倍数的特征:个位上的数字是0的数,既是2的倍数,又是5的倍数。
【详解】2的倍数有:106;60;130;280;6018
5的倍数有:35、60、75、130、280
2的倍数又是5的倍数有:60、130、280
发现:既是2的倍数又是5的倍数的末尾一定是0。
20.奇数;偶数;偶数
【分析】在自然数中,是2的倍数的数叫做偶数;不是2的倍数的数叫做奇数。据此解答。
【详解】奇数与奇数的积是奇数,比如3×5=15;
奇数与偶数的积是偶数,比如3×4=12;
偶数与偶数的积是偶数,比如2×4=8。
21.见详解
【分析】题干(1)中给出的方法,是根据数的组成进行改写,看这个数分别是由几个千、几个百、几个十和几个一组成,因为10,100,1000都是2或5的倍数,整十整百整千数无论乘几得到的数都是2或5的倍数,因此所以只要个位上的数是2或5的倍数,这个数就是2或5的倍数。
根据(1)的思路分析3的倍数的特征,利用乘法分配律,得到999、99、9分别乘一个数,因为999、99、9都是3的倍数,因此999、99、9无论乘几得到的数都是3的倍数,而余下的数相加刚好是各个数位上的数之和,因此只要一个数的各数位上的数字之和是3的倍数,这个数就是3的倍数。
根据这个思路,先写出一个9的倍数,将这个数根据数的组成进行改写,利用乘法分配律进行转化,可以得出与3的倍数的特征类似的9的倍数的特征。
【详解】9×181=1629
1629是9的倍数。
1629=1×1000+6×100+2×10+9×1
=1×(999+1)+6×(99+1)+2×(9+1)+9
=1×999+6×999+2×9+(1+6+2+9)
其中9,99,999都是9的倍数,括号中是这个数各个数位上的数,所以只要这些数的和是9的倍数,这个数就是9的倍数。
22.
见详解
【分析】(1)个位上是0,2,4,6或8的数,都是2的倍数。观察圈出来的数,则4的倍数都能被2整除。
(2)对圈出来的数观察发现,个位没有规律。所以只看个位不能判断一个数是不是4的倍数。一个整数的末尾两位数能被4整除,则这个数是4的倍数。
【详解】
(1)观察发现,圈出的4的倍数是2的倍数。
(2)只看个位,没有特别的规律。所以只看个位,不能判断一个数是不是4的倍数。
23.(1)×,13个位上的数是3,但不是3的倍数。
(2)√,11,23,35,47,59都是奇数。
(3)√,整数可以分为奇数和偶数,0是特殊的偶数。
【分析】(1)一个数各位上的数的和是3的倍数,这个数就是3的倍数。
(2)不是2的倍数的是奇数。
(3)一个整数不是奇数就是偶数。0是比较特殊的,但是能被2整除,所以0也是偶数。
【详解】(1)13个位上的数是3,但不是3的倍数。所以个位上是3,6,9的数,都是3的倍数说法错误。
(2)11,23,35,47,59都是奇数。所以个位上是1,3,5,7,9的数,都是奇数说法正确。
(3)整数可以分为奇数和偶数,0是特殊的偶数。所以在全部整数里,不是奇数就是偶数说法正确。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
