北师版数学必修54.2二元一次不等式(组)与平面区域
文档属性
| 名称 | 北师版数学必修54.2二元一次不等式(组)与平面区域 |

|
|
| 格式 | rar | ||
| 文件大小 | 48.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-04-15 23:15:00 | ||
图片预览




文档简介
课件15张PPT。4.1 二元一次不等式(组)与平面区域蚌埠三中 王磊一、引入:设用餐费x元,其他费用y元,由题意知,满足下面不等式确定平面直角坐标系中
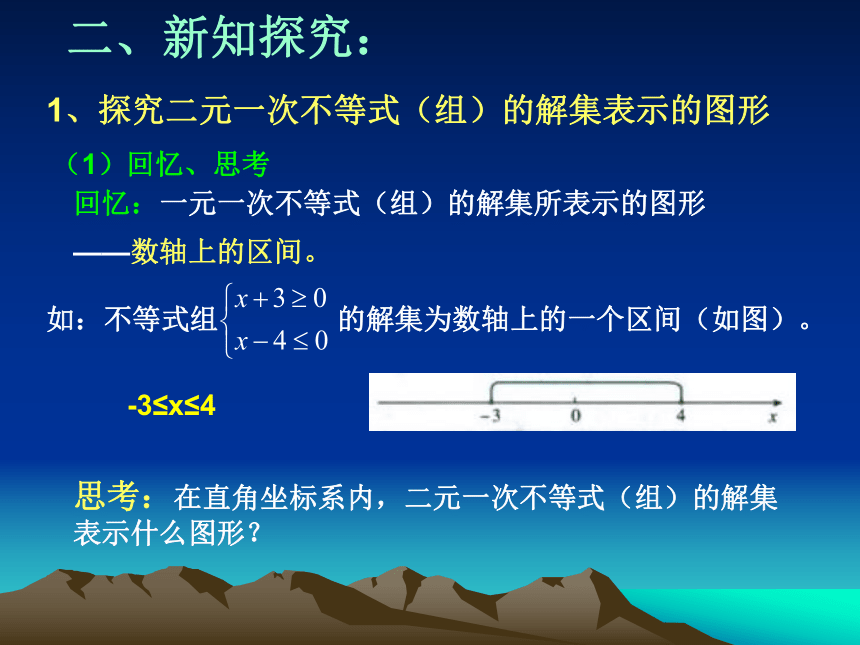
不等式组的解集区域二、新知探究: 1、探究二元一次不等式(组)的解集表示的图形 (1)回忆、思考 回忆:一元一次不等式(组)的解集所表示的图形
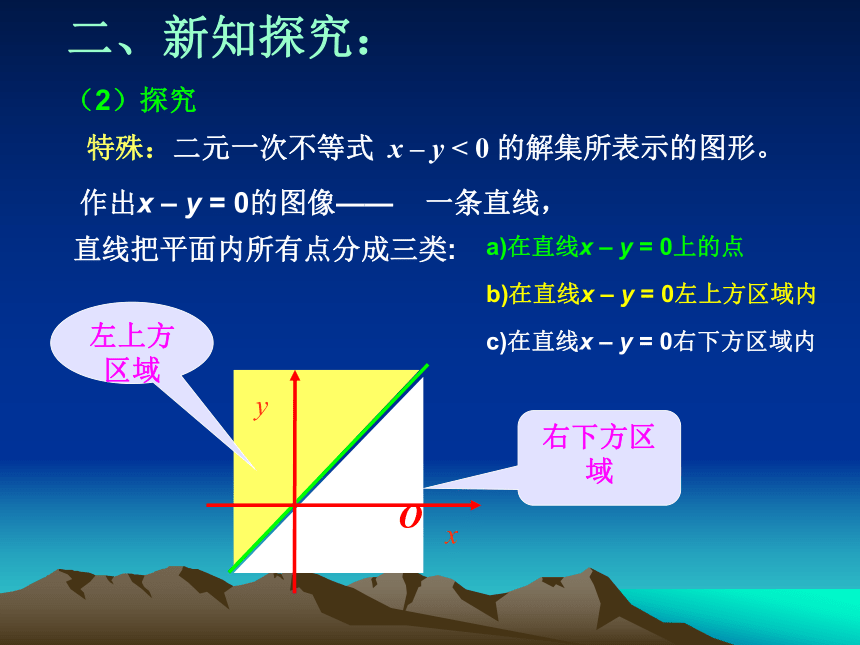
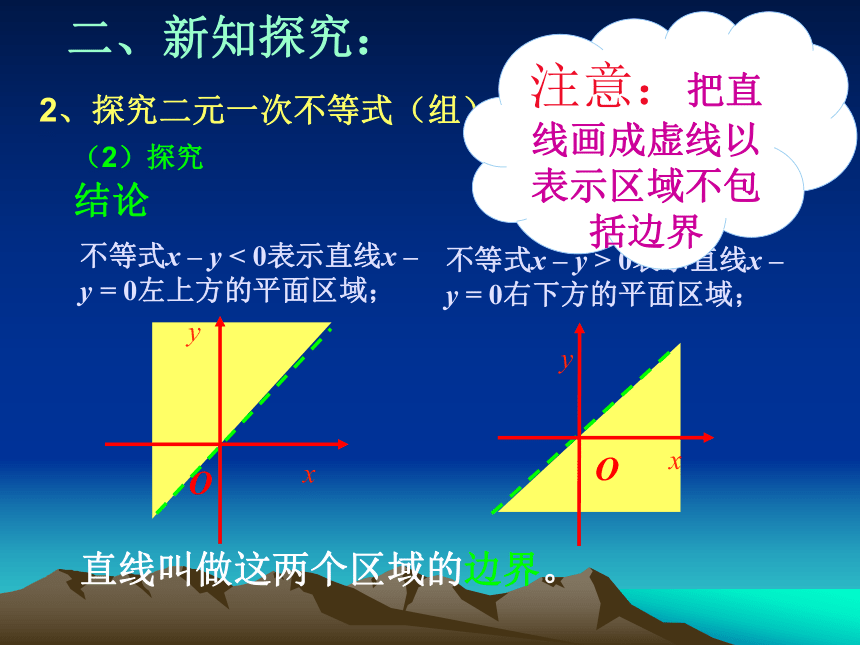
——数轴上的区间。 思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形? -3≤x≤4二、新知探究: (2)探究 特殊:二元一次不等式 x – y < 0 的解集所表示的图形。 作出x – y = 0的图像—— 一条直线,左上方区域右下方区域直线把平面内所有点分成三类:a)在直线x – y = 0上的点b)在直线x – y = 0左上方区域内 c)在直线x – y = 0右下方区域内二、新知探究: 2、探究二元一次不等式(组)的解集表示的图形 (2)探究 验证:在直线上任取点,例如点P(1,1),过点做与y轴平行的直线L1 .(1,1)二、新知探究: 2、探究二元一次不等式(组)的解集表示的图形 (2)探究 结论 在平面直角坐标系中,以二元一次不等式x – y > 0的解为坐标的点都在直线x – y = 0的右下方;反过来,直线x – y = 0右下方的点的坐标都满足不等式x – y > 0。 二、新知探究: 2、探究二元一次不等式(组)的解集表示的图形 (2)探究 结论 不等式x – y < 0表示直线x – y = 0左上方的平面区域; 不等式x – y > 0表示直线x – y = 0右下方的平面区域; 直线叫做这两个区域的边界。 注意:把直线画成虚线以表示区域不包括边界Oxy二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 (3)从特殊到一般情况: 二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线) 结论一 二元一次不等式表示相应直线的某一侧区域二、新知探究: 4.二元一次不等式表示哪个平面区域的判断方法 直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域,C≠0时,常把原点作为特殊点。结论二直线定界,特殊点定域。 解:(1)直线定界: 先画直线x + 2y – 3 = 0(画成虚线)(2)特殊点定域:取原点(0,0),代入x + 2y - 3,因为 0 + 2×0 –3 = -3 < 0所以,原点不在在x + 2y – 3>0表示的平面区域内,
不等式x + 2y – 3 > 0表示的区域如图所示。三、例题示范:课堂练习1:(1)画出不等式4x―3y≤12
表示的平面区域(2)画出不等式x≥1
表示的平面区域 的解集。例2、用平面区域表示不等式组三、例题示范:课堂练习2:课本第98页的练习1、3。 1、图中表示的平面区域满足不等式( )(A) x + y – 1<0 (B) x + y –1>0
(C) x – y – 1 <0 (D) x + y – 1>03、本节开头不等式组表示的
平面区域是B ⑴ 二元一次不等式表示平面区域:
直线某一侧所有点组成的平面区域。 ⑵ 判定方法:
直线定界,特殊点定域。小结: ⑶ 二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分。谢谢指导!作业:课本 P98 练习1 第4题
不等式组的解集区域二、新知探究: 1、探究二元一次不等式(组)的解集表示的图形 (1)回忆、思考 回忆:一元一次不等式(组)的解集所表示的图形
——数轴上的区间。 思考:在直角坐标系内,二元一次不等式(组)的解集表示什么图形? -3≤x≤4二、新知探究: (2)探究 特殊:二元一次不等式 x – y < 0 的解集所表示的图形。 作出x – y = 0的图像—— 一条直线,左上方区域右下方区域直线把平面内所有点分成三类:a)在直线x – y = 0上的点b)在直线x – y = 0左上方区域内 c)在直线x – y = 0右下方区域内二、新知探究: 2、探究二元一次不等式(组)的解集表示的图形 (2)探究 验证:在直线上任取点,例如点P(1,1),过点做与y轴平行的直线L1 .(1,1)二、新知探究: 2、探究二元一次不等式(组)的解集表示的图形 (2)探究 结论 在平面直角坐标系中,以二元一次不等式x – y > 0的解为坐标的点都在直线x – y = 0的右下方;反过来,直线x – y = 0右下方的点的坐标都满足不等式x – y > 0。 二、新知探究: 2、探究二元一次不等式(组)的解集表示的图形 (2)探究 结论 不等式x – y < 0表示直线x – y = 0左上方的平面区域; 不等式x – y > 0表示直线x – y = 0右下方的平面区域; 直线叫做这两个区域的边界。 注意:把直线画成虚线以表示区域不包括边界Oxy二、新知探究: 3、探究二元一次不等式(组)的解集表示的图形 (3)从特殊到一般情况: 二元一次不等式Ax + By + C>0在平面直角坐标系中表示直线Ax + By + C = 0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线) 结论一 二元一次不等式表示相应直线的某一侧区域二、新知探究: 4.二元一次不等式表示哪个平面区域的判断方法 直线Ax+By+C=0同一侧的所有点(x,y)代入Ax+By+C所得实数的符号都相同,只需在直线的某一侧任取一点(x0,y0),根据Ax+By+C的正负即可判断Ax+By+C>0表示直线的哪一侧区域,C≠0时,常把原点作为特殊点。结论二直线定界,特殊点定域。 解:(1)直线定界: 先画直线x + 2y – 3 = 0(画成虚线)(2)特殊点定域:取原点(0,0),代入x + 2y - 3,因为 0 + 2×0 –3 = -3 < 0所以,原点不在在x + 2y – 3>0表示的平面区域内,
不等式x + 2y – 3 > 0表示的区域如图所示。三、例题示范:课堂练习1:(1)画出不等式4x―3y≤12
表示的平面区域(2)画出不等式x≥1
表示的平面区域 的解集。例2、用平面区域表示不等式组三、例题示范:课堂练习2:课本第98页的练习1、3。 1、图中表示的平面区域满足不等式( )(A) x + y – 1<0 (B) x + y –1>0
(C) x – y – 1 <0 (D) x + y – 1>03、本节开头不等式组表示的
平面区域是B ⑴ 二元一次不等式表示平面区域:
直线某一侧所有点组成的平面区域。 ⑵ 判定方法:
直线定界,特殊点定域。小结: ⑶ 二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分。谢谢指导!作业:课本 P98 练习1 第4题
