2023-—2024学年人教版数学八年级下册16.1二次根式课件(22张ppt)
文档属性
| 名称 | 2023-—2024学年人教版数学八年级下册16.1二次根式课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 731.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第十六章 二次根式
16.1 二次根式
2. 什么叫做算术平方根 如何表示
正数的正的平方根叫做它的算术平方根;
0的算术平方根平方根是0. 即:
1. 什么叫做平方根 如何表示
若一个数的平方等于a, 则这个数就
叫做a的平方根. 即:
一、知识回顾
若 x2=a, 则 .
若x2=a(a≥0), 则 .
3. 平方根的性质:
正数有 平方根且互为 ;
0有 平方根就是 ;
负数 平方根.
两个
0
没有
相反数
一个
没有
没有
复习练习:
(1) 16的平方根是 , 算术平方根是 .
(2) 0的平方根是 , 算术平方根是 .
(3) 的平方根是 , 算术平方根是 .
(4) -7 平方根, 算术平方根.
±4
4
0
0
±2
2
二、新知探索①——二次根式
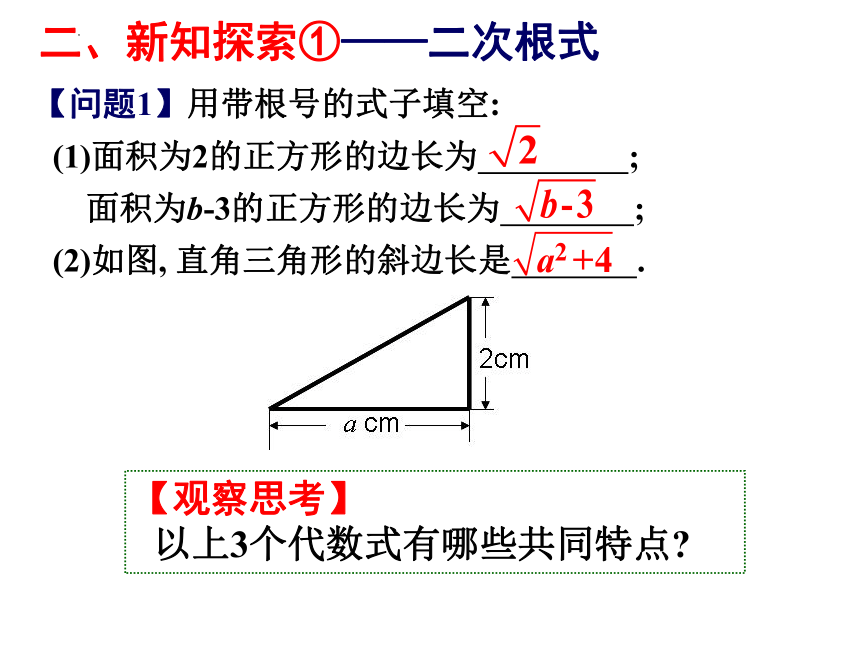
【问题1】用带根号的式子填空:
(1)面积为2的正方形的边长为 ;
面积为b-3的正方形的边长为 ;
(2)如图, 直角三角形的斜边长是 .
【观察思考】
以上3个代数式有哪些共同特点
【知识归纳】
形如 的式子叫做二次根式.
(3)被开方数可以是数, 也可以是含字母的代数式.
(2)被开方数必须是非负数, 即a≥0,
1. 二次根式的定义:
字母的取值使被开方数(式)为非负数.
2. 二次根式有意义的条件:
【注意事项】
(1)二次根式必须含有“ ”, 2叫做根指数(2通常省写),
中a叫做被开方数.
例1.下列各式中, 哪些是二次根式 哪些不是二次根式
是
不是
是
不是
被开方数必须是非负数
即a≥0.
【新知应用】
√
√
√
√
√
√
练习: 下列各式哪些是二次根式 哪些不是
二次根式 为什么
解: (1) ∵2x+3≥0
∴当 时,原式有意义.
例2. 当x为何值时, 下列各式有意义
(2) ∵2-4x≥0
∴当 时,原式有意义.
(3) ∵(x-3)2≥0
∴当x为任意实数时, 原式有意义.
解:(1)当x=-1时, 原式有意义;
(2)当x>-2时, 原式有意义;
(3)当x =1时, 原式有意义.
例3. 指出下列各式有意义的条件:
【对应练习】求下列各式中字母的取值范围:
x为任意实数
a为任意实数
【知识归纳①】
二次根式的性质: (1)
三、新知探索②——二次根式的性质
-6
1
通过快速计算,发现规律:
4
2
0
a
探索②——二次根式的性质
【知识归纳②】
二次根式的性质(2)
【示例2】 快速填空:
3
1.5
20
10
20
0
2
2
0.1
0.1
0
通过快速计算,发现规律:
探索②——二次根式的性质
a
0
-a
【知识归纳③】
二次根式的性质(3)
【思考】 与 是一样的吗 说说你的理由.
不同点:
(1)取值范围不同: 中的a可以取任何实数,
中的a 必须取非负数;
相同点: 当被开方数都是非负数时(a≥0),
(2)计算顺序不同: 是求a的平方的算术平方根,
是求a的算术平方根的平方.
(3)计算结果不同: , 而 .
例4. 化简:
(1)当
时,
(2)当
时,
(3)当
时,
【示例3】 快速填空:
7
1. 若 , 则x的取值范围是 .
2. 若 , 则x的取值范是 .
3. 化简: 的结果是 .
4. 当 时,
课堂练习①
例5. 在实数范围内分解因式:
解: 由图可知 a<0, b>0, |a|>|b|,
则a-b<0
例6. 实数a、b在数轴上的位置如图, 化简:
原式= |a| - |b| - |a-b|
=- a- b+(a-b)
=- a-b+a-b
=-2b.
本课小结
1.二次根式的定义:
2.二次根式的性质:
(1)形如 的式子叫做二次根式.
(2)当被开方数 时,二次根式有意义.
3.若 ,则x的取值范围是 .
1.数a、b在数轴上的位置如图所示,
化简
课堂练习②
1、已知 ,则 .
2、已知 是直角三角形的两边,且满足
,则第三边 的长为 .
3、已知 ,化简 .
4、已知 ,化简 .
能力提升
在实数范围内分解因式:
第十六章 二次根式
16.1 二次根式
2. 什么叫做算术平方根 如何表示
正数的正的平方根叫做它的算术平方根;
0的算术平方根平方根是0. 即:
1. 什么叫做平方根 如何表示
若一个数的平方等于a, 则这个数就
叫做a的平方根. 即:
一、知识回顾
若 x2=a, 则 .
若x2=a(a≥0), 则 .
3. 平方根的性质:
正数有 平方根且互为 ;
0有 平方根就是 ;
负数 平方根.
两个
0
没有
相反数
一个
没有
没有
复习练习:
(1) 16的平方根是 , 算术平方根是 .
(2) 0的平方根是 , 算术平方根是 .
(3) 的平方根是 , 算术平方根是 .
(4) -7 平方根, 算术平方根.
±4
4
0
0
±2
2
二、新知探索①——二次根式
【问题1】用带根号的式子填空:
(1)面积为2的正方形的边长为 ;
面积为b-3的正方形的边长为 ;
(2)如图, 直角三角形的斜边长是 .
【观察思考】
以上3个代数式有哪些共同特点
【知识归纳】
形如 的式子叫做二次根式.
(3)被开方数可以是数, 也可以是含字母的代数式.
(2)被开方数必须是非负数, 即a≥0,
1. 二次根式的定义:
字母的取值使被开方数(式)为非负数.
2. 二次根式有意义的条件:
【注意事项】
(1)二次根式必须含有“ ”, 2叫做根指数(2通常省写),
中a叫做被开方数.
例1.下列各式中, 哪些是二次根式 哪些不是二次根式
是
不是
是
不是
被开方数必须是非负数
即a≥0.
【新知应用】
√
√
√
√
√
√
练习: 下列各式哪些是二次根式 哪些不是
二次根式 为什么
解: (1) ∵2x+3≥0
∴当 时,原式有意义.
例2. 当x为何值时, 下列各式有意义
(2) ∵2-4x≥0
∴当 时,原式有意义.
(3) ∵(x-3)2≥0
∴当x为任意实数时, 原式有意义.
解:(1)当x=-1时, 原式有意义;
(2)当x>-2时, 原式有意义;
(3)当x =1时, 原式有意义.
例3. 指出下列各式有意义的条件:
【对应练习】求下列各式中字母的取值范围:
x为任意实数
a为任意实数
【知识归纳①】
二次根式的性质: (1)
三、新知探索②——二次根式的性质
-6
1
通过快速计算,发现规律:
4
2
0
a
探索②——二次根式的性质
【知识归纳②】
二次根式的性质(2)
【示例2】 快速填空:
3
1.5
20
10
20
0
2
2
0.1
0.1
0
通过快速计算,发现规律:
探索②——二次根式的性质
a
0
-a
【知识归纳③】
二次根式的性质(3)
【思考】 与 是一样的吗 说说你的理由.
不同点:
(1)取值范围不同: 中的a可以取任何实数,
中的a 必须取非负数;
相同点: 当被开方数都是非负数时(a≥0),
(2)计算顺序不同: 是求a的平方的算术平方根,
是求a的算术平方根的平方.
(3)计算结果不同: , 而 .
例4. 化简:
(1)当
时,
(2)当
时,
(3)当
时,
【示例3】 快速填空:
7
1. 若 , 则x的取值范围是 .
2. 若 , 则x的取值范是 .
3. 化简: 的结果是 .
4. 当 时,
课堂练习①
例5. 在实数范围内分解因式:
解: 由图可知 a<0, b>0, |a|>|b|,
则a-b<0
例6. 实数a、b在数轴上的位置如图, 化简:
原式= |a| - |b| - |a-b|
=- a- b+(a-b)
=- a-b+a-b
=-2b.
本课小结
1.二次根式的定义:
2.二次根式的性质:
(1)形如 的式子叫做二次根式.
(2)当被开方数 时,二次根式有意义.
3.若 ,则x的取值范围是 .
1.数a、b在数轴上的位置如图所示,
化简
课堂练习②
1、已知 ,则 .
2、已知 是直角三角形的两边,且满足
,则第三边 的长为 .
3、已知 ,化简 .
4、已知 ,化简 .
能力提升
在实数范围内分解因式:
