人教版七年级数学下册第五章 相交线与平行线章节练习题(含答案)
文档属性
| 名称 | 人教版七年级数学下册第五章 相交线与平行线章节练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 14:48:56 | ||
图片预览




文档简介
七年级数学下册第五章 相交线与平行线章节练习题
一、选择题(共30分)
1.(3分)如图所示,∠1和∠2是对顶角的图形有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)下列四个图案中,能用平移来分析其形成过程的是( )
A.B.C. D.
3.(3分)下列命题是真命题的是( )
A.垂直于同一条直线的两条直线平行
B.相等的角是对顶角
C.平行于同一条直线的两条直线平行
D.内错角相等
4.(3分)如图点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE
C.∠3=∠4 D.∠D+∠DAB=180°
5.(3分)如图,已知AB、CD、EF互相平行,且,EC为的角平分线,则的度数为( )
A.125° B.55° C.110° D.145°
6.(3分)如图,将三角形纸板ABC沿直线AB向右平行移动,使△CAB到达△DBE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
A.50° B.40° C.30° D.110°
7.(3分)如图,三角形ABC沿着由点B到点C的方向平移得到三角形DEF,已知BC=5,EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.8
8.(3分)如图,计划把河水l引到水池A中,先作AB⊥l,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是( )
A.两点之间线段最短
B.垂线段最短
C.过一点只能作一条直线
D.平面内,过一点有且只有一条直线与已知直线垂直
9.(3分)在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
10.(3分)将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )
A.43° B.47° C.30° D.60°
二、填空题(共30分)
11.(3分)如右图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是 °.
12.(3分)如图,已知∠1=∠2=∠3=59°,则∠4的度数为 °.
13.(3分)如图,已知AB∥CD,点E,F分别在AB,CD上,点G,H在两条平行线之间,∠AEG和∠GHF的平分线相交于点M.C若∠EGH=82°,∠HFD=20°,则∠M的度数为 °.
14.(3分)如图,将两个含角 的直角三角板的最长边靠在一起滑动,可知直角 边,依据是 .
15.(3分)将命题“对顶角相等”,改写成“如果………那么………”的形式
16.(3分)如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D'、C′的位置处,若∠1=56°,则∠EFB的度数是 .
17.(3分)如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°,则∠DON的度数是 .
18.(3分)如图,,则、、之间的数量关系是 .
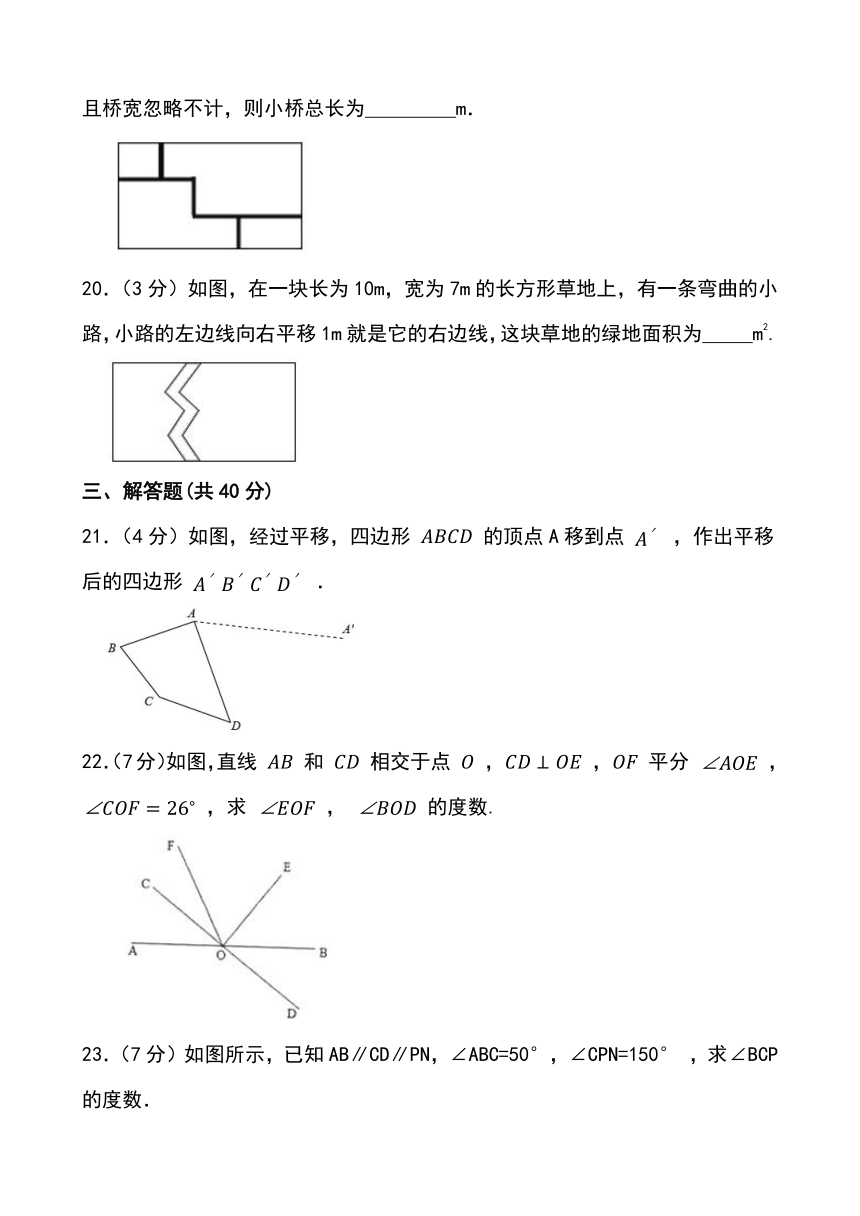
19.(3分)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为 m.
20.(3分)如图,在一块长为10m,宽为7m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m就是它的右边线,这块草地的绿地面积为 m2.
三、解答题(共40分)
21.(4分)如图,经过平移,四边形 的顶点A移到点 ,作出平移后的四边形 .
22.(7分)如图,直线 和 相交于点 , , 平分 , ,求 , 的度数.
23.(7分)如图所示,已知AB∥CD∥PN,∠ABC=50°,∠CPN=150° ,求∠BCP的度数.
24.(7分)如图,已知∠ABC+∠DCB=180°且∠1=∠2,试说明∠GFA+∠FDB=180°,请将下面的说明过程填写完整.
解:∵∠ABC+∠DCB=180°
∴CG∥AB,
∴∠1=▲ ,( )
∵∠1=∠2,
∴∠2=▲ ,( )
∴EG∥ ▲ ,( )
∴▲ +∠FDB=180°,
∵∠GFA=∠DFE,( )
∴∠GFA+∠FDB=180°.
25.(7分)如图,已知,点D在线段上,求证://.
26.(8分)如图,将直角△ABC(AC为斜边)沿直角边AB方向平移得到直角△DEF,已知BE=6,EF=10,CG=3,求阴影部分的面积.
答案解析部分
1.A
2.B
3.C
4.C
5.D
6.C
7.A
8.B
9.B
10.A
11.124
12.121
13.31
14.内错角相等,两直线平行
15.如果两个角为对顶角,那么它们相等。
16.62°
17.65°
18.
19.140
20.63
21.解:如图:四边形 即为所求.
22.解:∵
∴
∵
∴
∵ 平分
∴
∵
∴
23.解:∵AB∥CD∥PN(已知),
∴∠BCD=∠ABC=50°(两直线平行,内错角相等),
∠DCP=180°-∠CPN=180°-150°=30°(两直线平行,同旁内角互补),
∴∠BCP=∠BCD-∠DCP= 50°-30°=20°.
24.解:∵∠ABC+∠DCB=180°
∴CG∥AB,
∴∠1=∠FEA,(两直线平行,内错角相等)
∵∠1=∠2,
∴∠2=∠FEA,(等量代换)
∴EG∥BD,(同位角相等,两直线平行)
∴∠DFE+∠FDB=180°,
∵∠GFA=∠DFE,(对顶角相等)
∴∠GFA+∠FDB=180°.
25.证明:∵,
∴,
∴
∵,
∴,
∴.
26.解:依题意可得:阴影部分的面积=梯形BEFG的面积
又BE=6,EF=10,CG=3
∴BG=BC-CG=EF-CG=10-3=7
∴梯形BEFG的面积是 (BG+EF)·BE
=
=51
即所求阴影部分的面积是51.
故答案为:51.
一、选择题(共30分)
1.(3分)如图所示,∠1和∠2是对顶角的图形有( )
A.1个 B.2个 C.3个 D.4个
2.(3分)下列四个图案中,能用平移来分析其形成过程的是( )
A.B.C. D.
3.(3分)下列命题是真命题的是( )
A.垂直于同一条直线的两条直线平行
B.相等的角是对顶角
C.平行于同一条直线的两条直线平行
D.内错角相等
4.(3分)如图点E在BC的延长线上,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2 B.∠B=∠DCE
C.∠3=∠4 D.∠D+∠DAB=180°
5.(3分)如图,已知AB、CD、EF互相平行,且,EC为的角平分线,则的度数为( )
A.125° B.55° C.110° D.145°
6.(3分)如图,将三角形纸板ABC沿直线AB向右平行移动,使△CAB到达△DBE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为( )
A.50° B.40° C.30° D.110°
7.(3分)如图,三角形ABC沿着由点B到点C的方向平移得到三角形DEF,已知BC=5,EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.8
8.(3分)如图,计划把河水l引到水池A中,先作AB⊥l,垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是( )
A.两点之间线段最短
B.垂线段最短
C.过一点只能作一条直线
D.平面内,过一点有且只有一条直线与已知直线垂直
9.(3分)在一张透明的纸上画一条直线l,在l外任取一点Q,并折出过点Q且与l垂直的直线.这样的直线能折出( )
A.0条 B.1条 C.2条 D.3条
10.(3分)将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )
A.43° B.47° C.30° D.60°
二、填空题(共30分)
11.(3分)如右图,AB∥CD,直线l分别交AB、CD于E,F,∠1=56°,则∠2的度数是 °.
12.(3分)如图,已知∠1=∠2=∠3=59°,则∠4的度数为 °.
13.(3分)如图,已知AB∥CD,点E,F分别在AB,CD上,点G,H在两条平行线之间,∠AEG和∠GHF的平分线相交于点M.C若∠EGH=82°,∠HFD=20°,则∠M的度数为 °.
14.(3分)如图,将两个含角 的直角三角板的最长边靠在一起滑动,可知直角 边,依据是 .
15.(3分)将命题“对顶角相等”,改写成“如果………那么………”的形式
16.(3分)如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在点D'、C′的位置处,若∠1=56°,则∠EFB的度数是 .
17.(3分)如图,AB、CD相交于点O,OM平分∠BOD,∠MON是直角,∠AOC=50°,则∠DON的度数是 .
18.(3分)如图,,则、、之间的数量关系是 .
19.(3分)夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为 m.
20.(3分)如图,在一块长为10m,宽为7m的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m就是它的右边线,这块草地的绿地面积为 m2.
三、解答题(共40分)
21.(4分)如图,经过平移,四边形 的顶点A移到点 ,作出平移后的四边形 .
22.(7分)如图,直线 和 相交于点 , , 平分 , ,求 , 的度数.
23.(7分)如图所示,已知AB∥CD∥PN,∠ABC=50°,∠CPN=150° ,求∠BCP的度数.
24.(7分)如图,已知∠ABC+∠DCB=180°且∠1=∠2,试说明∠GFA+∠FDB=180°,请将下面的说明过程填写完整.
解:∵∠ABC+∠DCB=180°
∴CG∥AB,
∴∠1=▲ ,( )
∵∠1=∠2,
∴∠2=▲ ,( )
∴EG∥ ▲ ,( )
∴▲ +∠FDB=180°,
∵∠GFA=∠DFE,( )
∴∠GFA+∠FDB=180°.
25.(7分)如图,已知,点D在线段上,求证://.
26.(8分)如图,将直角△ABC(AC为斜边)沿直角边AB方向平移得到直角△DEF,已知BE=6,EF=10,CG=3,求阴影部分的面积.
答案解析部分
1.A
2.B
3.C
4.C
5.D
6.C
7.A
8.B
9.B
10.A
11.124
12.121
13.31
14.内错角相等,两直线平行
15.如果两个角为对顶角,那么它们相等。
16.62°
17.65°
18.
19.140
20.63
21.解:如图:四边形 即为所求.
22.解:∵
∴
∵
∴
∵ 平分
∴
∵
∴
23.解:∵AB∥CD∥PN(已知),
∴∠BCD=∠ABC=50°(两直线平行,内错角相等),
∠DCP=180°-∠CPN=180°-150°=30°(两直线平行,同旁内角互补),
∴∠BCP=∠BCD-∠DCP= 50°-30°=20°.
24.解:∵∠ABC+∠DCB=180°
∴CG∥AB,
∴∠1=∠FEA,(两直线平行,内错角相等)
∵∠1=∠2,
∴∠2=∠FEA,(等量代换)
∴EG∥BD,(同位角相等,两直线平行)
∴∠DFE+∠FDB=180°,
∵∠GFA=∠DFE,(对顶角相等)
∴∠GFA+∠FDB=180°.
25.证明:∵,
∴,
∴
∵,
∴,
∴.
26.解:依题意可得:阴影部分的面积=梯形BEFG的面积
又BE=6,EF=10,CG=3
∴BG=BC-CG=EF-CG=10-3=7
∴梯形BEFG的面积是 (BG+EF)·BE
=
=51
即所求阴影部分的面积是51.
故答案为:51.
