第二十八章 锐角三角函数压轴题特训(含解析)
文档属性
| 名称 | 第二十八章 锐角三角函数压轴题特训(含解析) | 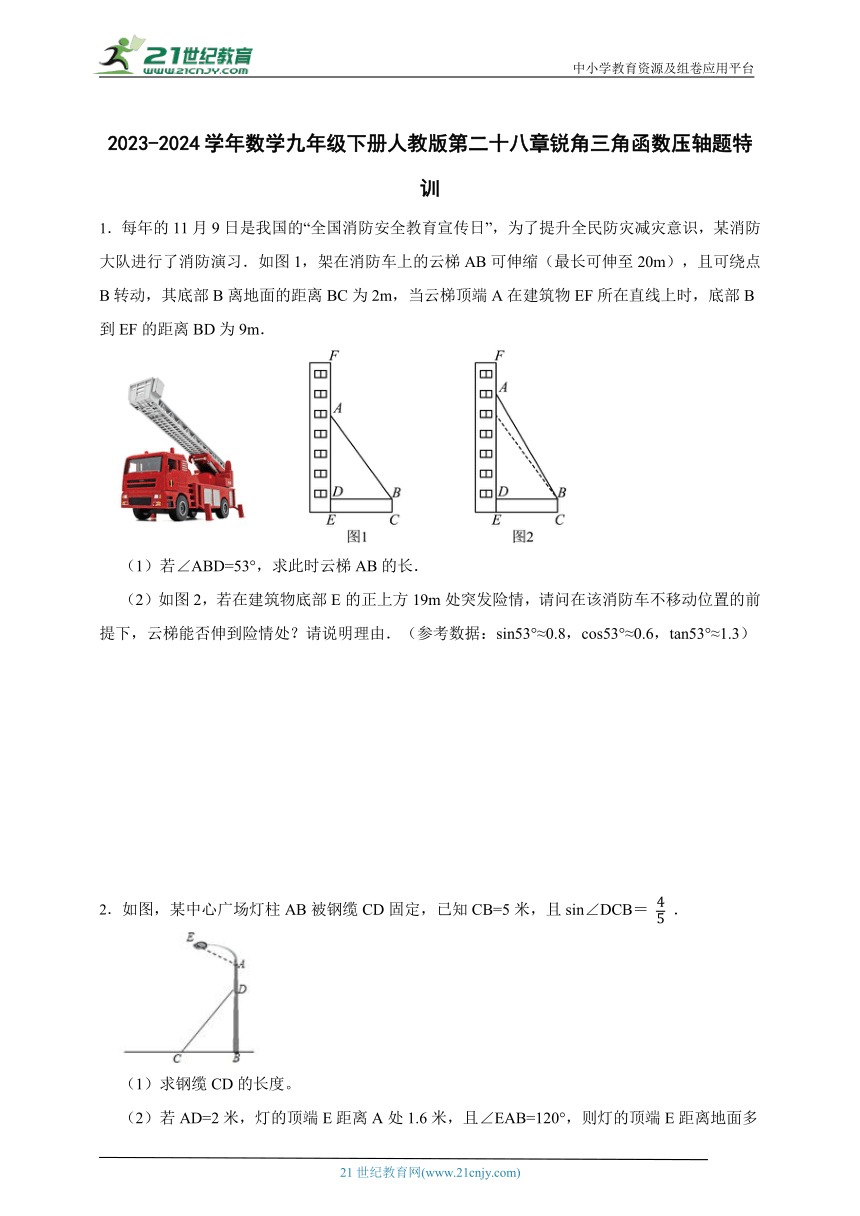 | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 20:35:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册人教版第二十八章锐角三角函数压轴题特训
1.每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
2.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB= .
(1)求钢缆CD的长度。
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
3.某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
(1)如图2,在点观察所测物体最高点,当量角器零刻度线上两点均在视线上时,测得视线与铅垂线所夹的锐角为,设仰角为,请直接用含的代数式示.
(2)如图3,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点分别测得气球的仰角为,为,地面上点在同一水平直线上,,求气球离地面的高度.(参考数据:,)
4.如图,在河流两边有甲、乙两座山,现在从甲山处的位置向乙山处拉电线.已知甲山上点到河边的距离米,点到的垂直高度为120米;乙山的坡比为,乙山上点到河边的距离米,从处看处的俯角为25°(参考值:,,)
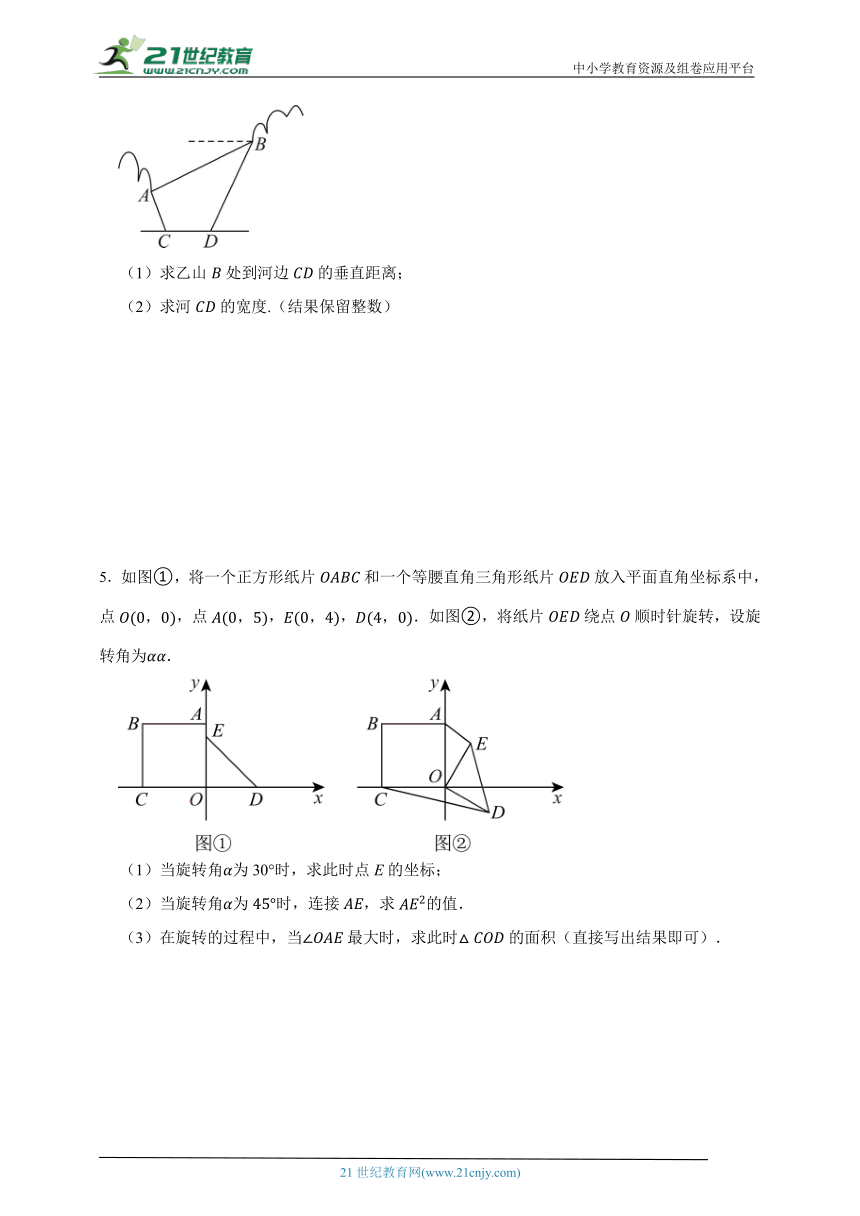
(1)求乙山处到河边的垂直距离;
(2)求河的宽度.(结果保留整数)
5.如图①,将一个正方形纸片和一个等腰直角三角形纸片放入平面直角坐标系中,点,点,,.如图②,将纸片绕点顺时针旋转,设旋转角为.
(1)当旋转角为30°时,求此时点E的坐标;
(2)当旋转角为时,连接,求的值.
(3)在旋转的过程中,当最大时,求此时的面积(直接写出结果即可).
6.一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)求点D转动到点D′的路径长;
(2)求点D到直线EF的距离(结果精确到0.1cm).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
7.如图1,矩形中,过作于点是延长线上一点,连接,过点作,分别交于点.
(1)若
①求证
②求的长
(2)如图2,若平分,,,求的长
8.如图,中,以为直径的交于点E.平分,过点E作于点D,延长交的延长线于点P.
(1)求证:是的切线;
(2)若,求的长.
9.我国于2019年6月5日首次完成运载火箭海上发射,达到了发射技术的新高度.如图,运载火箭海面发射站点M与岸边雷达站N处在同一水平高度.当火箭到达点A处时,测得点A距离发射站点M的垂直高度为9千米,雷达站N测得A处的仰角为,火箭继续垂直上升到达点B处,此时海岸边N处的雷达测得B处的仰角为,根据下面提供的参考数据计算下列问题∶
(1)求火箭海面发射站点M与岸边雷达站N的距离;
(2)求火箭所在点B处距发射站点M处的高度.
(参考数据∶,,,,,)
10.如图,梯形ABCD中,AD∥BC,BC=42,cosB=,以点C为圆心,CM为半径的⊙C交射线CD于点N,交射线CA于点G.
(1)求线段AD的长;
(2)设线段CM=x,=y,当点N在线段CD上时,并写出x的取值范围;
(3)联结DM,当∠NMC=2∠DMN时,求线段CM的长.
11.如图,在矩形ABCD中,AB=2,BC=4,点E在直线AB上,连结DE,过点A作AF⊥DE交直线BC于点F,以AE、AF为邻边作平行四边形AEGF.直线DG交直线AB于点H.
(1)当点E在线段AB上时,求证:△ABF ∽△DAE.
(2)当AE=2时,求EH的长.
(3)在点E的运动过程中,是否存在某一位置,使得△EGH为等腰三角形.若存在,求AE的长.
12.图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)
13.如图,中,,,.是边上的一点,(与、不重合)连接,作,交于点,交于点
(1)求、的长
(2)设,,求与的函数关系式,并写出定义域
(3)连接,当与相似时,求的长
14.如图,梯形中,,,,,.点M在射线上,点N在射线上,且,联结,交射线于点G.
(1)求线段的长;
(2)设线段,,当点N在线段上时,试求出y关于x的函数关系式,并写出x的取值范围;
(3)联结,当时,求线段的长.
答案解析部分
1.【答案】(1)解:在Rt△ABD中,∠ABD=53°,BD=9m,
∴AB==15(m),
∴此时云梯AB的长为15m;
(2)解:在该消防车不移动位置的前提下,云梯能伸到险情处,
理由:由题意得:
DE=BC=2m,
∵AE=19m,
∴AD=AE-DE=19-2=17(m),
在Rt△ABD中,BD=9m,
∴AB= (m),
∵m<20m,
∴在该消防车不移动位置的前提下,云梯能伸到险情处.
2.【答案】(1)解:在Rt△DCB中,sin∠DCB= = ,∴设DB=4x,DC=5x,由勾股定理得:∴ ,解得 或 (舍),∴CD= 米,DB= 米;
(2)解:如图,
过点E作EF⊥AB于点F,∵∠EAB=120°,∴∠EAF=60°,∴AF=AE·cos∠EAF=1.6× =0.8(米),∴FB=AF+AD+DB=0.8+2+ = (米),∴灯的顶端E距离地面 米.
3.【答案】(1)解:如图所示:
由题意知,
在中,,则,即,
;
(2)解:如图所示:
,
在中,,由等腰直角三角形性质得到,
在中,,
由,
即,
解得,
气球离地面的高度.
4.【答案】(1)解:如图,过B作于点F,
∵乙山的坡比为,
∴,
设米,则米,
∴(米),
又米,
∴,
∴,
∴米,
答:乙山B处到河边的垂直距离为360米;
(2)解:过A作于点E,过A作于点H,则四边形为矩形,
,
∴米,,
∴(米),
∵从B处看A处的俯角为,
∴,
在中,,
∴(米),
∴(米),
在中,由勾股定理得:(米),
由(1)可知,米,
∴(米),
答:河的宽度约为195米.
5.【答案】(1)过点作于,
由题意,
,
,
;
(2)过点作于,如图②,
由题意得,
,
,
,
,
,
,
;
(3)由题意知点在以为圆,为半径的圆上运动,当时,的值最大,此时,.
过点作轴于,过点作于.
,
,
,,
∴,
,
,,,
.
6.【答案】(1)解:∵BD'∥EF,∠BEF=108°,
∴∠D'BE=180°-∠BEF=72°,
∵∠DBE=108°,
∴∠DBD'=∠DBE-∠D'BE=108°-72°=36°,
∵BD=6,
∴点D转动到点D′的路径长为 = π(cm);
(2)解:过D作DG⊥BD'于G,过E作EH⊥BD'于H,如图:
Rt△BDG中,DG=BD sin36°≈6×0.59=3.54(cm),
Rt△BEH中,HE=BE sin72°≈4×0.95=3.80(cm),
∴DG+HE=3.54cm+3.80cm=7.34m≈7.3cm,
∵BD'∥EF,
∴点D到直线EF的距离约为7.3cm,
答:点D到直线EF的距离约为7.3cm.
7.【答案】(1)①∵,
∴,
∴,
∴;
②∵四边形是矩形,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
即,
∴,
∴;
(2)∵平分,
∴
设,
∵
∴
又∵
∴
∵
∴
∴,则,
∵,
∴
即
又∵
∴,则,
如图所示,过点分别作的垂线,垂足分别为,则
在中,
∴
∵
即
∴
∴
则,
过点作于点,
∵是的角平分线,
∴
∴;
设,则,
∴
∴,
∴,
在中,则,,则,
∴
在中,,
∴,
在中,
∴
∴
∵,则,
∴,
∴,
∴,
∵,,
∴,
解得:,
∴.
8.【答案】(1)证明:如图,连接,
,
,
平分,
,
,
,
,
,
是的切线;
(2)解:
设,则,
,解得,
,
,
根据勾股定理可得,,
,
是直径,
,
,
,
,
,
,
.
9.【答案】(1)解:∵ 当火箭到达点A处时,测得点A距离发射站点M的垂直高度为9千米,雷达站N测得A处的仰角为37°,
∴AM=9,∠ANM=37°,
在Rt△AMN中
即
解之:MN≈
答:火箭海面发射站点M与岸边雷达站N的距离为12km
(2)解:∵ 火箭继续垂直上升到达点B处,此时海岸边N处的雷达测得B处的仰角为,
∴∠MNB=70°,
在Rt△BMN中
BM=MNtan∠MNB=12×tan0°≈12×2.75=33km.
答:火箭所在点B处距发射站点M处的高度为33km
10.【答案】(1)解:过点A作AH⊥BC于H,过点D作DE⊥AC于E,
∵在Rt△ABH中,∠AHB=90°,,
∴BH=10,AH=24,
∴CH=BC﹣BH=32.
∵在Rt△AHC中,∠AHC=90°,
,
∵AD=DC,
∴∠DAC=∠DCA,.
∵AD∥BC,
∴∠DAC=∠ACB=∠DCA,
在Rt△ADE中,,
∴AD=CD=25;
(2)解:延长MN交AD的延长线于点F.
∵AD∥BC,
∴
∵CM=CN=x,CD=AD=25,
∴DN=25﹣x,
∴,
∴DF=25﹣x,
∴AF=50﹣x,
∴;
(3)解:当点N在CD上时,
∵CM=CN,
∴∠NMC=∠MNC.
∵∠NMC=6∠DMN,∠MNC=∠DMN+∠MDN,
∴∠DMN=∠MDN.
∴DN=MN=25﹣x,
∵
∴.
∴,
∴,
即CM=;
当点N在CD的延长线上时,DN=x﹣25,
延长DA交射线MN于点P.
∵∠NMC=2∠DMN,
∴∠NMD=∠DMC,
∵AD∥BC,∠NMC=∠MNC,
∴∠NPD=∠MNC,,
∴DN=PD=x﹣25.
∵AD∥BC,
∴∠PDM=∠DMC,
∴∠NMD=∠PDM.
∴PM=PD=x﹣25.
∴,
∴x=55,即CM=55,
综上所述,线段CM的长为.
11.【答案】(1)证明:∵,
∴.
∵四边形ABCD为矩形,
∴,
∴.
又∵,
∴△ABF ∽△DAE;
(2)解:①当E在点A上方时,
由AB=2,得点E与B重合,如图,
∵△ABF∽△DAE,
∴,
∴,
∴.
∵四边形AEGF是平行四边形,,
∴GF=AB=CD=2,,
即在△GMF和△DMC中,,
∴△GMF≌△DMC(AAS),
∴,
∴.
∵,
∴△MGF∽△MHE,
∴,即,
∴EH=;
②当E在点A下方时,如图,
∵FG=AE=CD=2,
∴G、A、D共线
此时,H与A重合,
∴HE=2.
综上可知,EH的长为或2;
(3)解:①当点H在点A的上方时,如图,△EGH为钝角三角形
由等腰△EGH得,GH=GE.
作GQ⊥BH于点Q,则HQ=EQ.
∴四边形BFGQ为矩形,
∴QB=GF=EA,
∴QE=AB=2,
∴HQ=EQ=2.
设AE=2t,
由(1)得,
∴,
∴GQ=BF=t.
∵QG//AD,
∴△HQG ∽△HAD
∴,即,
解得 (舍去)
∴AE=2t=;
②当点H在点A的下方时,
(ⅰ)若GH=GE,如图,作GQ⊥BE于点Q,则HQ=EQ.
∵AE=GF=BQ,
∴QE=AB=2,HQ=EQ=2.
设AE=2t,同理:GQ=BF=t
由,得,
解得(舍去)
∴AE=2t=;
(ⅱ)若HG=HE,如图,
∴∠2=∠1.
同理△ABF ∽△DAE,则,
∵AF=GE,AF∥GE,AF⊥DE,
∴GE⊥DE,,
∴△DGE是直角三角形,
∵∠2+∠3=90°,∠GDE+∠1=90°,
∴∠3=∠1,
∴tan∠3= tan∠GDE==,
∴=,
∴AE=2AD=8;
(ⅲ)若EG=EH,如图,
同理可求出tan∠HGE=2,
则tan∠AHD=tan∠GHQ=tan∠HGE=2,
∴.
设AE=2t,
同理可得:GQ=BF=t,EQ=AB=2,
由,得,解得,
∴ AE=2t=.
综上可知:AE=或8或.
12.【答案】(1)解:如图,过M作MN⊥AB于N,交BA的延长线于N,
在Rt△OMN中,∠NOM=60°,OM=1.2,∴∠M=30°,
∴ON OM=0.6,
∴NB=ON+OB=3.3+0.6=3.9,
即点M到地面的距离是3.9米;
(2)解:取CE=0.65,EH=2.55,∴HB=3.9﹣2.55﹣0.65=0.7,
过H作GH⊥BC,交OM于G,过O作OP⊥GH于P,
∵∠GOP=30°,∴tan30° ,
∴GP OP 0.404,
∴GH=3.3+0.404=3.704≈3.70>3.5,
∴货车能安全通过.
13.【答案】(1)解:中,,
∵,即,
∴,
∴,
∴,,
在中,,
在中,,
∴;
(2)解:∵,,
∴,即,
同理可得,
∴,
∴,
即,
∴,
∴,
当时,,
∴,
∴;
(3)解:∵,
①当,时,,
∴,即,
解得(负值已舍去).
②当时,
∴,
∴,
∵,
∴,
∴,
综上所述,的长为或.
14.【答案】(1)解:过点A作于点H,过点D作于点E,
在中,,
∴,
∴,
在中,,由勾股定理得到,
,
∵,
∴,,
∵,
∴,
在中,,
∴;
(2)解:延长交的延长线于点F,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(3)解:当点N在上,如图,
∵,
∴,
∴是等腰三角形,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
解得,
即,
当点N在的延长线上时,,
延长交射线于点P,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
经检验,是分式方程的解,
即,
综上所述,线段的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学九年级下册人教版第二十八章锐角三角函数压轴题特训
1.每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处?请说明理由.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
2.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且sin∠DCB= .
(1)求钢缆CD的长度。
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
3.某综合实践研究小组为了测量观察目标时的仰角和俯角,利用量角器和铅锤自制了一个简易测角仪,如图1所示.
(1)如图2,在点观察所测物体最高点,当量角器零刻度线上两点均在视线上时,测得视线与铅垂线所夹的锐角为,设仰角为,请直接用含的代数式示.
(2)如图3,为了测量广场上空气球离地面的高度,该小组利用自制简易测角仪在点分别测得气球的仰角为,为,地面上点在同一水平直线上,,求气球离地面的高度.(参考数据:,)
4.如图,在河流两边有甲、乙两座山,现在从甲山处的位置向乙山处拉电线.已知甲山上点到河边的距离米,点到的垂直高度为120米;乙山的坡比为,乙山上点到河边的距离米,从处看处的俯角为25°(参考值:,,)
(1)求乙山处到河边的垂直距离;
(2)求河的宽度.(结果保留整数)
5.如图①,将一个正方形纸片和一个等腰直角三角形纸片放入平面直角坐标系中,点,点,,.如图②,将纸片绕点顺时针旋转,设旋转角为.
(1)当旋转角为30°时,求此时点E的坐标;
(2)当旋转角为时,连接,求的值.
(3)在旋转的过程中,当最大时,求此时的面积(直接写出结果即可).
6.一酒精消毒瓶如图1,AB为喷嘴,△BCD为按压柄,CE为伸缩连杆,BE和EF为导管,其示意图如图2,∠DBE=∠BEF=108°,BD=6cm,BE=4cm.当按压柄△BCD按压到底时,BD转动到BD′,此时BD′∥EF(如图3).
(1)求点D转动到点D′的路径长;
(2)求点D到直线EF的距离(结果精确到0.1cm).
(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73,sin72°≈0.95,cos72°≈0.31,tan72°≈3.08)
7.如图1,矩形中,过作于点是延长线上一点,连接,过点作,分别交于点.
(1)若
①求证
②求的长
(2)如图2,若平分,,,求的长
8.如图,中,以为直径的交于点E.平分,过点E作于点D,延长交的延长线于点P.
(1)求证:是的切线;
(2)若,求的长.
9.我国于2019年6月5日首次完成运载火箭海上发射,达到了发射技术的新高度.如图,运载火箭海面发射站点M与岸边雷达站N处在同一水平高度.当火箭到达点A处时,测得点A距离发射站点M的垂直高度为9千米,雷达站N测得A处的仰角为,火箭继续垂直上升到达点B处,此时海岸边N处的雷达测得B处的仰角为,根据下面提供的参考数据计算下列问题∶
(1)求火箭海面发射站点M与岸边雷达站N的距离;
(2)求火箭所在点B处距发射站点M处的高度.
(参考数据∶,,,,,)
10.如图,梯形ABCD中,AD∥BC,BC=42,cosB=,以点C为圆心,CM为半径的⊙C交射线CD于点N,交射线CA于点G.
(1)求线段AD的长;
(2)设线段CM=x,=y,当点N在线段CD上时,并写出x的取值范围;
(3)联结DM,当∠NMC=2∠DMN时,求线段CM的长.
11.如图,在矩形ABCD中,AB=2,BC=4,点E在直线AB上,连结DE,过点A作AF⊥DE交直线BC于点F,以AE、AF为邻边作平行四边形AEGF.直线DG交直线AB于点H.
(1)当点E在线段AB上时,求证:△ABF ∽△DAE.
(2)当AE=2时,求EH的长.
(3)在点E的运动过程中,是否存在某一位置,使得△EGH为等腰三角形.若存在,求AE的长.
12.图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据: 1.73,结果精确到0.01米)
13.如图,中,,,.是边上的一点,(与、不重合)连接,作,交于点,交于点
(1)求、的长
(2)设,,求与的函数关系式,并写出定义域
(3)连接,当与相似时,求的长
14.如图,梯形中,,,,,.点M在射线上,点N在射线上,且,联结,交射线于点G.
(1)求线段的长;
(2)设线段,,当点N在线段上时,试求出y关于x的函数关系式,并写出x的取值范围;
(3)联结,当时,求线段的长.
答案解析部分
1.【答案】(1)解:在Rt△ABD中,∠ABD=53°,BD=9m,
∴AB==15(m),
∴此时云梯AB的长为15m;
(2)解:在该消防车不移动位置的前提下,云梯能伸到险情处,
理由:由题意得:
DE=BC=2m,
∵AE=19m,
∴AD=AE-DE=19-2=17(m),
在Rt△ABD中,BD=9m,
∴AB= (m),
∵m<20m,
∴在该消防车不移动位置的前提下,云梯能伸到险情处.
2.【答案】(1)解:在Rt△DCB中,sin∠DCB= = ,∴设DB=4x,DC=5x,由勾股定理得:∴ ,解得 或 (舍),∴CD= 米,DB= 米;
(2)解:如图,
过点E作EF⊥AB于点F,∵∠EAB=120°,∴∠EAF=60°,∴AF=AE·cos∠EAF=1.6× =0.8(米),∴FB=AF+AD+DB=0.8+2+ = (米),∴灯的顶端E距离地面 米.
3.【答案】(1)解:如图所示:
由题意知,
在中,,则,即,
;
(2)解:如图所示:
,
在中,,由等腰直角三角形性质得到,
在中,,
由,
即,
解得,
气球离地面的高度.
4.【答案】(1)解:如图,过B作于点F,
∵乙山的坡比为,
∴,
设米,则米,
∴(米),
又米,
∴,
∴,
∴米,
答:乙山B处到河边的垂直距离为360米;
(2)解:过A作于点E,过A作于点H,则四边形为矩形,
,
∴米,,
∴(米),
∵从B处看A处的俯角为,
∴,
在中,,
∴(米),
∴(米),
在中,由勾股定理得:(米),
由(1)可知,米,
∴(米),
答:河的宽度约为195米.
5.【答案】(1)过点作于,
由题意,
,
,
;
(2)过点作于,如图②,
由题意得,
,
,
,
,
,
,
;
(3)由题意知点在以为圆,为半径的圆上运动,当时,的值最大,此时,.
过点作轴于,过点作于.
,
,
,,
∴,
,
,,,
.
6.【答案】(1)解:∵BD'∥EF,∠BEF=108°,
∴∠D'BE=180°-∠BEF=72°,
∵∠DBE=108°,
∴∠DBD'=∠DBE-∠D'BE=108°-72°=36°,
∵BD=6,
∴点D转动到点D′的路径长为 = π(cm);
(2)解:过D作DG⊥BD'于G,过E作EH⊥BD'于H,如图:
Rt△BDG中,DG=BD sin36°≈6×0.59=3.54(cm),
Rt△BEH中,HE=BE sin72°≈4×0.95=3.80(cm),
∴DG+HE=3.54cm+3.80cm=7.34m≈7.3cm,
∵BD'∥EF,
∴点D到直线EF的距离约为7.3cm,
答:点D到直线EF的距离约为7.3cm.
7.【答案】(1)①∵,
∴,
∴,
∴;
②∵四边形是矩形,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
即,
∴,
∴;
(2)∵平分,
∴
设,
∵
∴
又∵
∴
∵
∴
∴,则,
∵,
∴
即
又∵
∴,则,
如图所示,过点分别作的垂线,垂足分别为,则
在中,
∴
∵
即
∴
∴
则,
过点作于点,
∵是的角平分线,
∴
∴;
设,则,
∴
∴,
∴,
在中,则,,则,
∴
在中,,
∴,
在中,
∴
∴
∵,则,
∴,
∴,
∴,
∵,,
∴,
解得:,
∴.
8.【答案】(1)证明:如图,连接,
,
,
平分,
,
,
,
,
,
是的切线;
(2)解:
设,则,
,解得,
,
,
根据勾股定理可得,,
,
是直径,
,
,
,
,
,
,
.
9.【答案】(1)解:∵ 当火箭到达点A处时,测得点A距离发射站点M的垂直高度为9千米,雷达站N测得A处的仰角为37°,
∴AM=9,∠ANM=37°,
在Rt△AMN中
即
解之:MN≈
答:火箭海面发射站点M与岸边雷达站N的距离为12km
(2)解:∵ 火箭继续垂直上升到达点B处,此时海岸边N处的雷达测得B处的仰角为,
∴∠MNB=70°,
在Rt△BMN中
BM=MNtan∠MNB=12×tan0°≈12×2.75=33km.
答:火箭所在点B处距发射站点M处的高度为33km
10.【答案】(1)解:过点A作AH⊥BC于H,过点D作DE⊥AC于E,
∵在Rt△ABH中,∠AHB=90°,,
∴BH=10,AH=24,
∴CH=BC﹣BH=32.
∵在Rt△AHC中,∠AHC=90°,
,
∵AD=DC,
∴∠DAC=∠DCA,.
∵AD∥BC,
∴∠DAC=∠ACB=∠DCA,
在Rt△ADE中,,
∴AD=CD=25;
(2)解:延长MN交AD的延长线于点F.
∵AD∥BC,
∴
∵CM=CN=x,CD=AD=25,
∴DN=25﹣x,
∴,
∴DF=25﹣x,
∴AF=50﹣x,
∴;
(3)解:当点N在CD上时,
∵CM=CN,
∴∠NMC=∠MNC.
∵∠NMC=6∠DMN,∠MNC=∠DMN+∠MDN,
∴∠DMN=∠MDN.
∴DN=MN=25﹣x,
∵
∴.
∴,
∴,
即CM=;
当点N在CD的延长线上时,DN=x﹣25,
延长DA交射线MN于点P.
∵∠NMC=2∠DMN,
∴∠NMD=∠DMC,
∵AD∥BC,∠NMC=∠MNC,
∴∠NPD=∠MNC,,
∴DN=PD=x﹣25.
∵AD∥BC,
∴∠PDM=∠DMC,
∴∠NMD=∠PDM.
∴PM=PD=x﹣25.
∴,
∴x=55,即CM=55,
综上所述,线段CM的长为.
11.【答案】(1)证明:∵,
∴.
∵四边形ABCD为矩形,
∴,
∴.
又∵,
∴△ABF ∽△DAE;
(2)解:①当E在点A上方时,
由AB=2,得点E与B重合,如图,
∵△ABF∽△DAE,
∴,
∴,
∴.
∵四边形AEGF是平行四边形,,
∴GF=AB=CD=2,,
即在△GMF和△DMC中,,
∴△GMF≌△DMC(AAS),
∴,
∴.
∵,
∴△MGF∽△MHE,
∴,即,
∴EH=;
②当E在点A下方时,如图,
∵FG=AE=CD=2,
∴G、A、D共线
此时,H与A重合,
∴HE=2.
综上可知,EH的长为或2;
(3)解:①当点H在点A的上方时,如图,△EGH为钝角三角形
由等腰△EGH得,GH=GE.
作GQ⊥BH于点Q,则HQ=EQ.
∴四边形BFGQ为矩形,
∴QB=GF=EA,
∴QE=AB=2,
∴HQ=EQ=2.
设AE=2t,
由(1)得,
∴,
∴GQ=BF=t.
∵QG//AD,
∴△HQG ∽△HAD
∴,即,
解得 (舍去)
∴AE=2t=;
②当点H在点A的下方时,
(ⅰ)若GH=GE,如图,作GQ⊥BE于点Q,则HQ=EQ.
∵AE=GF=BQ,
∴QE=AB=2,HQ=EQ=2.
设AE=2t,同理:GQ=BF=t
由,得,
解得(舍去)
∴AE=2t=;
(ⅱ)若HG=HE,如图,
∴∠2=∠1.
同理△ABF ∽△DAE,则,
∵AF=GE,AF∥GE,AF⊥DE,
∴GE⊥DE,,
∴△DGE是直角三角形,
∵∠2+∠3=90°,∠GDE+∠1=90°,
∴∠3=∠1,
∴tan∠3= tan∠GDE==,
∴=,
∴AE=2AD=8;
(ⅲ)若EG=EH,如图,
同理可求出tan∠HGE=2,
则tan∠AHD=tan∠GHQ=tan∠HGE=2,
∴.
设AE=2t,
同理可得:GQ=BF=t,EQ=AB=2,
由,得,解得,
∴ AE=2t=.
综上可知:AE=或8或.
12.【答案】(1)解:如图,过M作MN⊥AB于N,交BA的延长线于N,
在Rt△OMN中,∠NOM=60°,OM=1.2,∴∠M=30°,
∴ON OM=0.6,
∴NB=ON+OB=3.3+0.6=3.9,
即点M到地面的距离是3.9米;
(2)解:取CE=0.65,EH=2.55,∴HB=3.9﹣2.55﹣0.65=0.7,
过H作GH⊥BC,交OM于G,过O作OP⊥GH于P,
∵∠GOP=30°,∴tan30° ,
∴GP OP 0.404,
∴GH=3.3+0.404=3.704≈3.70>3.5,
∴货车能安全通过.
13.【答案】(1)解:中,,
∵,即,
∴,
∴,
∴,,
在中,,
在中,,
∴;
(2)解:∵,,
∴,即,
同理可得,
∴,
∴,
即,
∴,
∴,
当时,,
∴,
∴;
(3)解:∵,
①当,时,,
∴,即,
解得(负值已舍去).
②当时,
∴,
∴,
∵,
∴,
∴,
综上所述,的长为或.
14.【答案】(1)解:过点A作于点H,过点D作于点E,
在中,,
∴,
∴,
在中,,由勾股定理得到,
,
∵,
∴,,
∵,
∴,
在中,,
∴;
(2)解:延长交的延长线于点F,
∵,
∴,
∵,
∴,
∴,
∴,
∴;
(3)解:当点N在上,如图,
∵,
∴,
∴是等腰三角形,
∵,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
解得,
即,
当点N在的延长线上时,,
延长交射线于点P,
∵,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
经检验,是分式方程的解,
即,
综上所述,线段的长为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
