第三章 圆压轴题特训(含解析)
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册北师大版第三章圆压轴题特训
1.如图,在中,,的平分线交于点D,的平分线交于点E.以上的点O为圆心,为半径作,恰好过点E.
(1)求证:是的切线;
(2)若,,求的半径.
2.如图,是的直径,,都是上的点,且平分,过点作的垂线交的延长线于点,交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
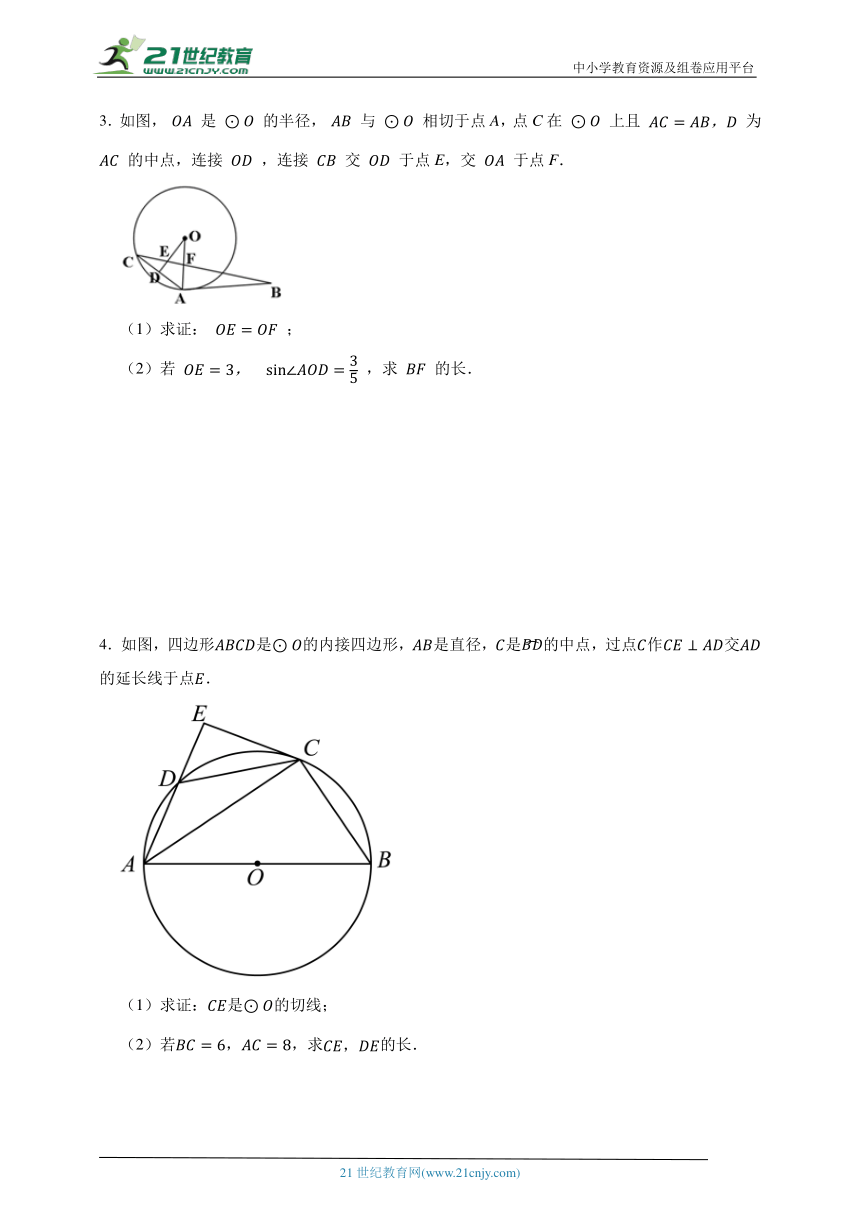
3.如图, 是 的半径, 与 相切于点A,点C在 上且 为 的中点,连接 ,连接 交 于点E,交 于点F.
(1)求证: ;
(2)若 ,求 的长.
4.如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
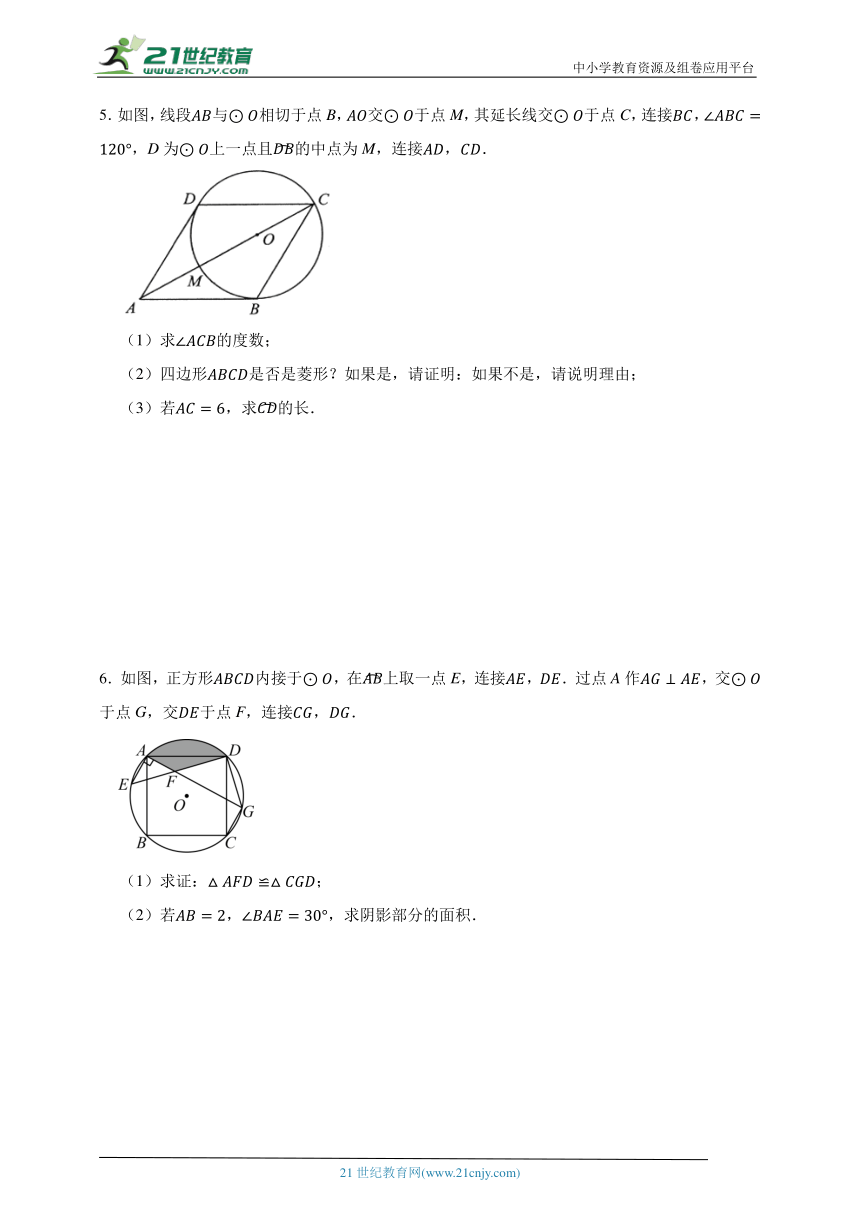
5.如图,线段与相切于点B,交于点M,其延长线交于点C,连接,,D为上一点且的中点为M,连接,.
(1)求的度数;
(2)四边形是否是菱形?如果是,请证明:如果不是,请说明理由;
(3)若,求的长.
6.如图,正方形内接于,在上取一点E,连接,.过点A作,交于点G,交于点F,连接,.
(1)求证:;
(2)若,,求阴影部分的面积.
7.如图,,为的直径,为上一点,过点的切线与的延长线交于点,,点是的中点,弦,相交于点.
(1)求的度数;
(2)若,求直径的长.
8.如图,点D,E在以为直径的上,的平分线交于点B,连接,,,过点E作,垂足为H,交于点F.
(1)求证:;
(2)若,求的长.
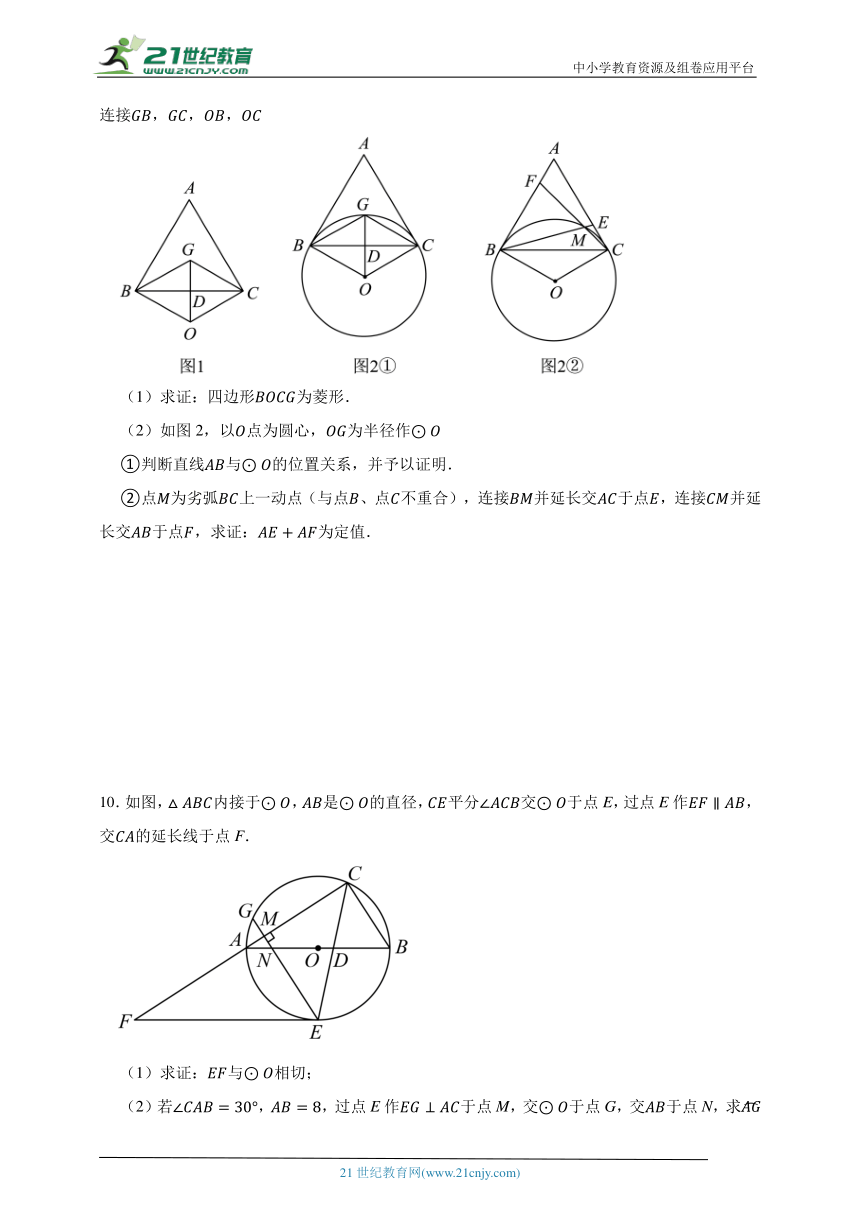
9.如图1,点为等边的重心,点为边的中点,连接并延长至点,使得,连接,,,
(1)求证:四边形为菱形.
(2)如图2,以点为圆心,为半径作
①判断直线与的位置关系,并予以证明.
②点为劣弧上一动点(与点、点不重合),连接并延长交于点,连接并延长交于点,求证:为定值.
10.如图,内接于,是的直径,平分交于点E,过点E作,交的延长线于点F.
(1)求证:与相切;
(2)若,,过点E作于点M,交于点G,交于点N,求的长.
11.如图,已知是的直径,直线是的切线,切点为,,垂足为.连接.
(1)求证:平分;
(2)若,,求的半径.
12.如图,在中,,以为直径的与交于点D,点是的中点,连接,.
(1)求证:是的切线;
(2)若,,求的长;
(3)在(2)的条件下,点P是上一动点,求的最大值.
13.如图,已知等腰,,以为直径作交于点,过作于点,交延长线于点.
(1)求证:是的切线.
(2)若,,求图中阴影部分的面积结果用表示.
14.如图1,在中,为的直径,点为上一点,为的平分线交于点,连接交于点.
(1)求的度数;
(2)如图2,过点作的切线交延长线于点,过点作交于点.若,求的长.
答案解析部分
1.【答案】(1)证明:连接,
由题意可知,
∴,
∵平分,
∴,
∴,
∴,
又∵,
∴,
即,
∴是的切线;
(2)解:过点作,
∵平分,,,
∴,
∵,,
∴,
∴,则,
∴,
∴,
∵,
∴,
∴,即:,
可得:,
∴的半径为.
2.【答案】(1)证明:连接.
于点E,
,
平分,
,
,
,
,
.
,即于点D,且是半径,
是的切线.
(2)解:连接交于点G,
是的直径,
.
.
四边形是矩形
,,即于点G.
在中,
,,
,
,是的半径,
,
在中,
,,
,
,
.
3.【答案】(1)证明:∵ 与 相切于点A,
∴∠OAB=90°,
∴∠B+∠AFB=90°,
∵D是 的中点,
∴OD⊥AC,
∴∠C+∠CED=90°,
∵ ,
∴∠B=∠C,
∴∠AFB=∠CED,
又∵∠AFB=∠OFE,∠CED=∠OEF,
∴OE=OF,
(2)解:∵在 中, ,
∴设AD=3x,则OA=5x,OD=4x,
∵D是 的中点,
∴CD=AD=3x,
∴DE=4x-3,
又∵OE=OF=3,
∴AF=5x-3,
∵∠B=∠C, =6x,
∴tanB=tanC,即: ,
∴ ,解得:x=1,
∴AF=5x-3=2,AB=6x=6,
∴BF .
4.【答案】(1)证明:连接
∵为的中点,
∴=,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,为半径,
∴为的切线,
(2)解:∵为直径,
∴,
∵,
∴,
又∵,,
∴,
∴,即,
∴,
∵,
∴,
在中,由勾股定理得:
.
5.【答案】(1)解:如图,连接,
∵线段与相切于点B,
∴,而,
∴,
∵,
∴;
(2)解:四边形是菱形,理由如下:
∵的中点为M,,
∴,即,而,
∴,
∴,
∵的中点为M,为直径,
∴,
∴,
∵,,
∴,
∴,
∴,
∴四边形是菱形.
(3)解:如图,连接,,交于,
∵,,
∴为等边三角形,
∴,
∴,
∵菱形,,
∴,,
∴,
∵,
∴,
∴,
∴,
,
∴的长为.
6.【答案】(1)证明:如图,连接,
∵,则,
∴,
∵正方形,
∴,,
∴,
∴,
∵,
∴.
(2)解:如图,连接,,过作于,设,在上取Q,使,
∵O为正方形中心,
∴,,而,
∴,,
∵,
∴,
∴,,
∵,
∴,
∴,而,
∴,
∴,
∴,,
而正方形的边长,
∴,
解得:,
∴,
∵,,,
∴,
∴,
而,
∴.
7.【答案】(1)解:∵与相切于点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴,
∴;
(2)解:如图,连接,
∵是直径,
∴,
∵点是的中点,
∴,
∴,
在中,
∵,,
∴,
在中,
∵,
∴,
∴的直径的长为.
8.【答案】(1)证明:连接,
∵,
∴,
∵是直径,
∴,
∴,
∴,
∴,
又∵,
∴,
∴,
∴;
(2)解:如图,连接,
∵的平分线交于点B,
∴,
∴,
∴,
∵是直径,
∴,
∵,
∴,,
∴.
9.【答案】(1)证明:如图,延长交于点,连接,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,
∴ ,,
∵,
∴四边形是平行四边形,
∵ ,
∴四边形为菱形;
(2)解:①解:直线是的切线,理由如下:延长交于点,连接,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,,
∴为的角平分线,
∴,
∵四边形是菱形,
∴,
∴,
∴,
∴直线是的切线;
②证明:在优弧上取一点,连接、,
由①得,
∵,
∴,
∴,
∴,
∵四边形内接于,
∴,
∴,
∵,
∴,
∴,
∵,,
∴
∴
∵
∴,即为定值.
10.【答案】(1)证明:如图,连接,
是的直径,
,
平分交于点E,
,
,
,
,
,
是的半径,
与相切;
(2)解:如图,连接,,
,,
,
,
是等边三角形,
,
,
,,
,
,
,
,是的直径,
,
.
即的长为.
11.【答案】(1)证明:连接,
∵直线是的切线,
∴,
∵,
∴,
∴,
∵,
∴,
∴,即平分;
(2)解:连接,过点O作于F,则,
∵,,
∴,
∴,
∴,
∴,
∴,
即的半径为.
12.【答案】(1)证明:连接,如图所示,
∵为的直径,
∴,
∴,
∵点为的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵是的半径,
∴与相切;
(2)解:由(1)知,,
∵是的中点,
∴,
∴,
∵,
∴,,
又∵在中,,即:,
∴(负值以舍去),
∴;
(3)解:设的边高为,
由(2)可知,
又∵是直径,
∴,
∴,
∴,
∴当取最大值时,也取最大值,
又∵,
∴当取最大值时,取最大值,
此时边高为取最大值为半径,
∴,
∴
∴,
∴,
综上所述:的最大值为.
13.【答案】(1)证明:如图,连接,
,
,
,
,
,
,
,
,
是的半径,
是的切线
(2)解:如图,连接,
设的半径为,
在中,,,
,
,
,
,
,
,
,为的中点,
是的中位线,
是中点,
,
是的的直径,
,
,
,
,
,
,
阴影部分的面积四边形的面积扇形的面积
.
14.【答案】(1)∵是的直径,
∴,
∵平分,
∴,即,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
(2)如图,连接,设,
则,,,
∵是的直径,
∴,
在中,由勾股定理得:
由(1)得:,
∴,
由勾股定理得:,,
∴,
∴,整理得:,
解得:或(舍去),
∴,
∴,
∵是的切线,
∴,
∵,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学九年级下册北师大版第三章圆压轴题特训
1.如图,在中,,的平分线交于点D,的平分线交于点E.以上的点O为圆心,为半径作,恰好过点E.
(1)求证:是的切线;
(2)若,,求的半径.
2.如图,是的直径,,都是上的点,且平分,过点作的垂线交的延长线于点,交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
3.如图, 是 的半径, 与 相切于点A,点C在 上且 为 的中点,连接 ,连接 交 于点E,交 于点F.
(1)求证: ;
(2)若 ,求 的长.
4.如图,四边形是的内接四边形,是直径,是的中点,过点作交的延长线于点.
(1)求证:是的切线;
(2)若,,求的长.
5.如图,线段与相切于点B,交于点M,其延长线交于点C,连接,,D为上一点且的中点为M,连接,.
(1)求的度数;
(2)四边形是否是菱形?如果是,请证明:如果不是,请说明理由;
(3)若,求的长.
6.如图,正方形内接于,在上取一点E,连接,.过点A作,交于点G,交于点F,连接,.
(1)求证:;
(2)若,,求阴影部分的面积.
7.如图,,为的直径,为上一点,过点的切线与的延长线交于点,,点是的中点,弦,相交于点.
(1)求的度数;
(2)若,求直径的长.
8.如图,点D,E在以为直径的上,的平分线交于点B,连接,,,过点E作,垂足为H,交于点F.
(1)求证:;
(2)若,求的长.
9.如图1,点为等边的重心,点为边的中点,连接并延长至点,使得,连接,,,
(1)求证:四边形为菱形.
(2)如图2,以点为圆心,为半径作
①判断直线与的位置关系,并予以证明.
②点为劣弧上一动点(与点、点不重合),连接并延长交于点,连接并延长交于点,求证:为定值.
10.如图,内接于,是的直径,平分交于点E,过点E作,交的延长线于点F.
(1)求证:与相切;
(2)若,,过点E作于点M,交于点G,交于点N,求的长.
11.如图,已知是的直径,直线是的切线,切点为,,垂足为.连接.
(1)求证:平分;
(2)若,,求的半径.
12.如图,在中,,以为直径的与交于点D,点是的中点,连接,.
(1)求证:是的切线;
(2)若,,求的长;
(3)在(2)的条件下,点P是上一动点,求的最大值.
13.如图,已知等腰,,以为直径作交于点,过作于点,交延长线于点.
(1)求证:是的切线.
(2)若,,求图中阴影部分的面积结果用表示.
14.如图1,在中,为的直径,点为上一点,为的平分线交于点,连接交于点.
(1)求的度数;
(2)如图2,过点作的切线交延长线于点,过点作交于点.若,求的长.
答案解析部分
1.【答案】(1)证明:连接,
由题意可知,
∴,
∵平分,
∴,
∴,
∴,
又∵,
∴,
即,
∴是的切线;
(2)解:过点作,
∵平分,,,
∴,
∵,,
∴,
∴,则,
∴,
∴,
∵,
∴,
∴,即:,
可得:,
∴的半径为.
2.【答案】(1)证明:连接.
于点E,
,
平分,
,
,
,
,
.
,即于点D,且是半径,
是的切线.
(2)解:连接交于点G,
是的直径,
.
.
四边形是矩形
,,即于点G.
在中,
,,
,
,是的半径,
,
在中,
,,
,
,
.
3.【答案】(1)证明:∵ 与 相切于点A,
∴∠OAB=90°,
∴∠B+∠AFB=90°,
∵D是 的中点,
∴OD⊥AC,
∴∠C+∠CED=90°,
∵ ,
∴∠B=∠C,
∴∠AFB=∠CED,
又∵∠AFB=∠OFE,∠CED=∠OEF,
∴OE=OF,
(2)解:∵在 中, ,
∴设AD=3x,则OA=5x,OD=4x,
∵D是 的中点,
∴CD=AD=3x,
∴DE=4x-3,
又∵OE=OF=3,
∴AF=5x-3,
∵∠B=∠C, =6x,
∴tanB=tanC,即: ,
∴ ,解得:x=1,
∴AF=5x-3=2,AB=6x=6,
∴BF .
4.【答案】(1)证明:连接
∵为的中点,
∴=,
∴,
又∵,
∴,
∴,
∴,
又∵,
∴,为半径,
∴为的切线,
(2)解:∵为直径,
∴,
∵,
∴,
又∵,,
∴,
∴,即,
∴,
∵,
∴,
在中,由勾股定理得:
.
5.【答案】(1)解:如图,连接,
∵线段与相切于点B,
∴,而,
∴,
∵,
∴;
(2)解:四边形是菱形,理由如下:
∵的中点为M,,
∴,即,而,
∴,
∴,
∵的中点为M,为直径,
∴,
∴,
∵,,
∴,
∴,
∴,
∴四边形是菱形.
(3)解:如图,连接,,交于,
∵,,
∴为等边三角形,
∴,
∴,
∵菱形,,
∴,,
∴,
∵,
∴,
∴,
∴,
,
∴的长为.
6.【答案】(1)证明:如图,连接,
∵,则,
∴,
∵正方形,
∴,,
∴,
∴,
∵,
∴.
(2)解:如图,连接,,过作于,设,在上取Q,使,
∵O为正方形中心,
∴,,而,
∴,,
∵,
∴,
∴,,
∵,
∴,
∴,而,
∴,
∴,
∴,,
而正方形的边长,
∴,
解得:,
∴,
∵,,,
∴,
∴,
而,
∴.
7.【答案】(1)解:∵与相切于点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴,
∴;
(2)解:如图,连接,
∵是直径,
∴,
∵点是的中点,
∴,
∴,
在中,
∵,,
∴,
在中,
∵,
∴,
∴的直径的长为.
8.【答案】(1)证明:连接,
∵,
∴,
∵是直径,
∴,
∴,
∴,
∴,
又∵,
∴,
∴,
∴;
(2)解:如图,连接,
∵的平分线交于点B,
∴,
∴,
∴,
∵是直径,
∴,
∵,
∴,,
∴.
9.【答案】(1)证明:如图,延长交于点,连接,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,
∴ ,,
∵,
∴四边形是平行四边形,
∵ ,
∴四边形为菱形;
(2)解:①解:直线是的切线,理由如下:延长交于点,连接,
∵是等边三角形,是重心,点为边的中点,
∴中线过点,即、、三点共线,,,,
∴为的角平分线,
∴,
∵四边形是菱形,
∴,
∴,
∴,
∴直线是的切线;
②证明:在优弧上取一点,连接、,
由①得,
∵,
∴,
∴,
∴,
∵四边形内接于,
∴,
∴,
∵,
∴,
∴,
∵,,
∴
∴
∵
∴,即为定值.
10.【答案】(1)证明:如图,连接,
是的直径,
,
平分交于点E,
,
,
,
,
,
是的半径,
与相切;
(2)解:如图,连接,,
,,
,
,
是等边三角形,
,
,
,,
,
,
,
,是的直径,
,
.
即的长为.
11.【答案】(1)证明:连接,
∵直线是的切线,
∴,
∵,
∴,
∴,
∵,
∴,
∴,即平分;
(2)解:连接,过点O作于F,则,
∵,,
∴,
∴,
∴,
∴,
∴,
即的半径为.
12.【答案】(1)证明:连接,如图所示,
∵为的直径,
∴,
∴,
∵点为的中点,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵是的半径,
∴与相切;
(2)解:由(1)知,,
∵是的中点,
∴,
∴,
∵,
∴,,
又∵在中,,即:,
∴(负值以舍去),
∴;
(3)解:设的边高为,
由(2)可知,
又∵是直径,
∴,
∴,
∴,
∴当取最大值时,也取最大值,
又∵,
∴当取最大值时,取最大值,
此时边高为取最大值为半径,
∴,
∴
∴,
∴,
综上所述:的最大值为.
13.【答案】(1)证明:如图,连接,
,
,
,
,
,
,
,
,
是的半径,
是的切线
(2)解:如图,连接,
设的半径为,
在中,,,
,
,
,
,
,
,
,为的中点,
是的中位线,
是中点,
,
是的的直径,
,
,
,
,
,
,
阴影部分的面积四边形的面积扇形的面积
.
14.【答案】(1)∵是的直径,
∴,
∵平分,
∴,即,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
(2)如图,连接,设,
则,,,
∵是的直径,
∴,
在中,由勾股定理得:
由(1)得:,
∴,
由勾股定理得:,,
∴,
∴,整理得:,
解得:或(舍去),
∴,
∴,
∵是的切线,
∴,
∵,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
