第二章 二次函数压轴题特训(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册北师大版第二章二次函数压轴题特训
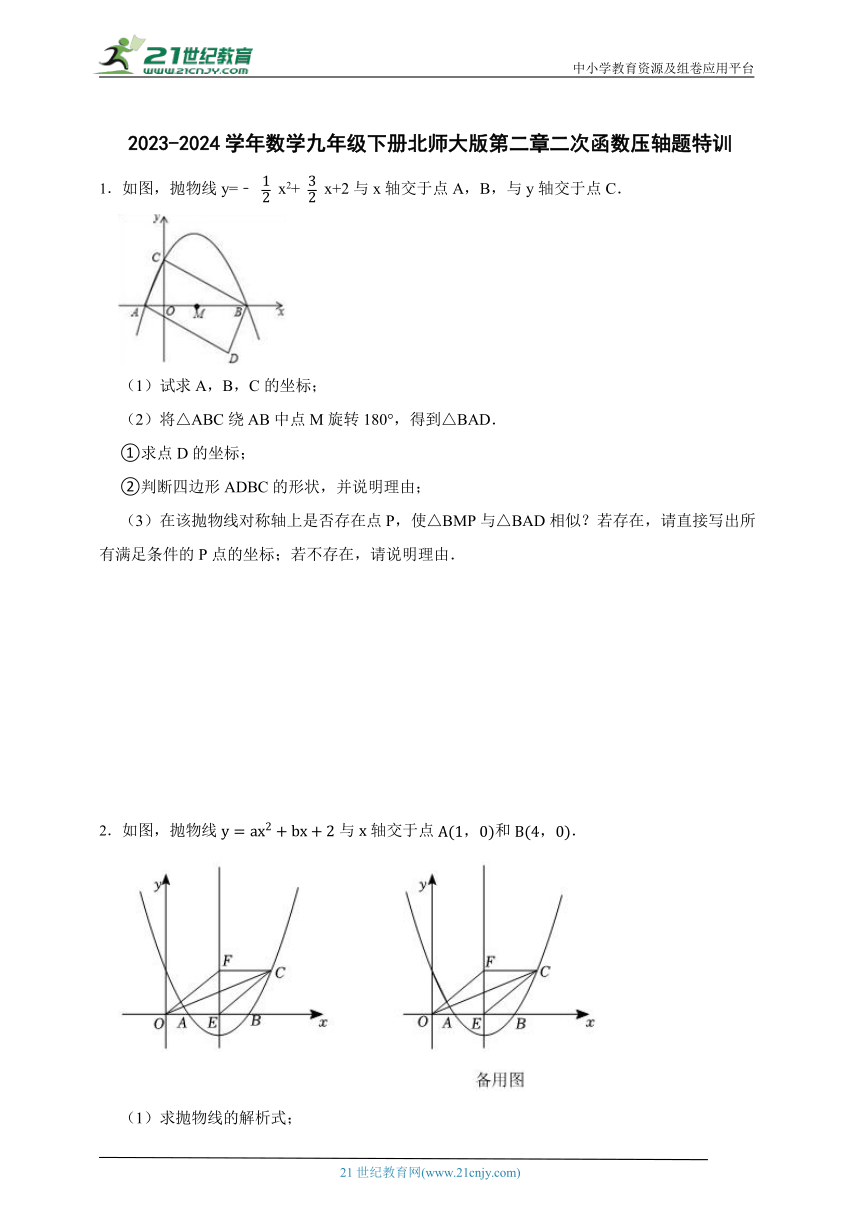
1.如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
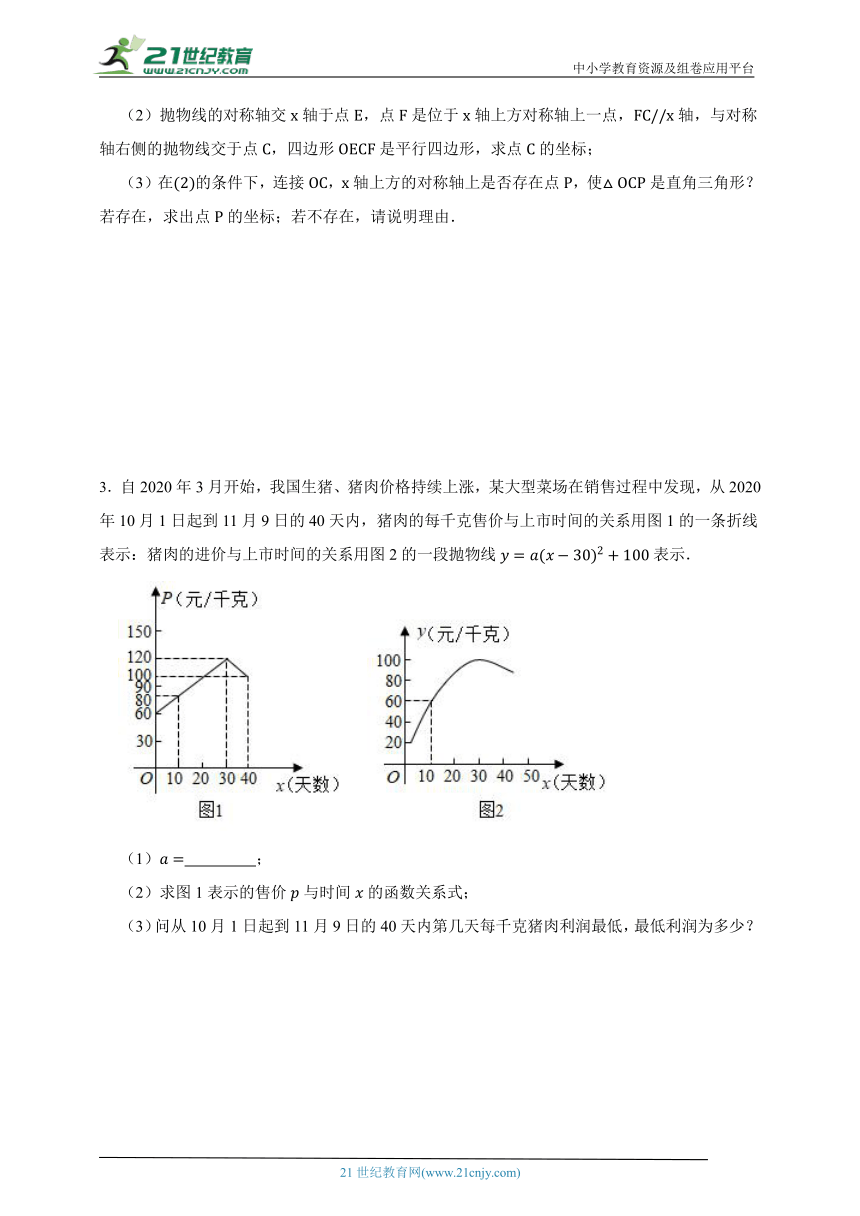
2.如图,抛物线与轴交于点和.
(1)求抛物线的解析式;
(2)抛物线的对称轴交轴于点,点是位于轴上方对称轴上一点,轴,与对称轴右侧的抛物线交于点,四边形是平行四边形,求点的坐标;
(3)在的条件下,连接,轴上方的对称轴上是否存在点,使是直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
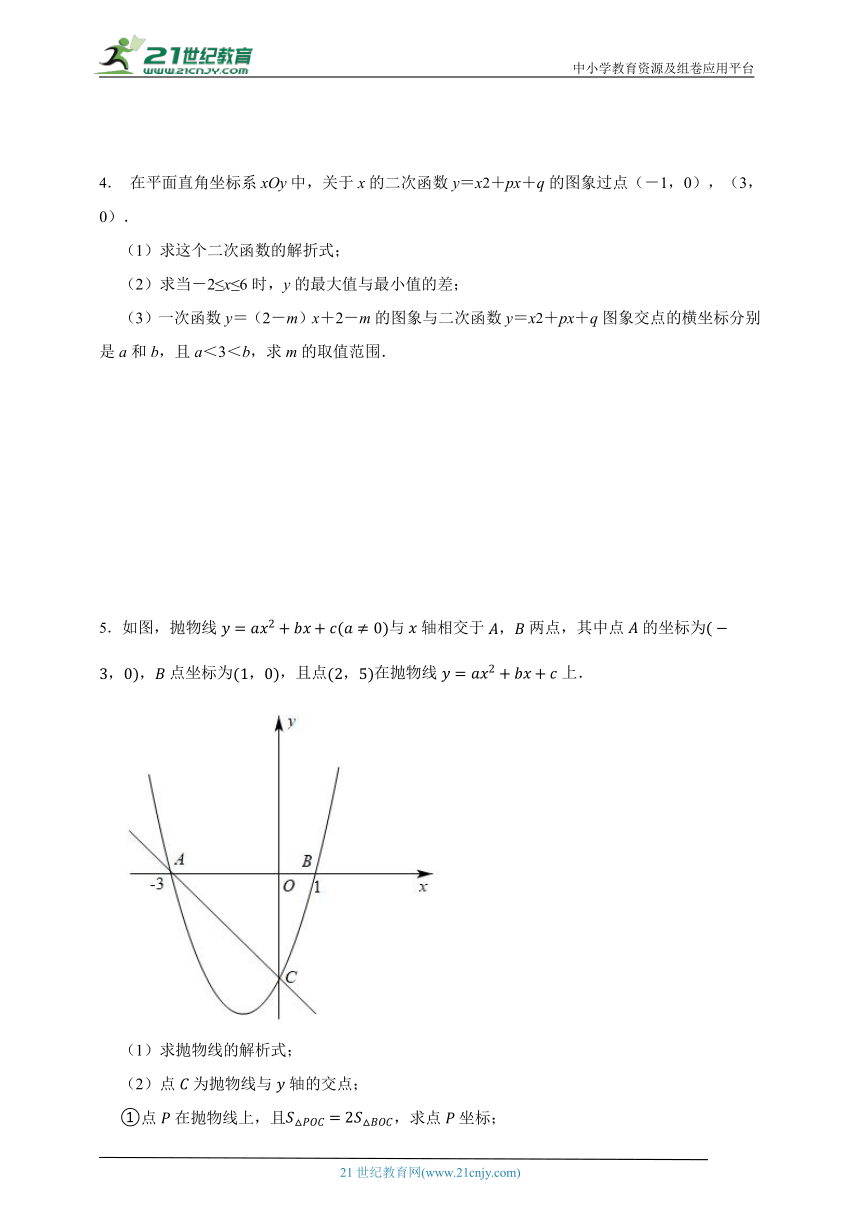
3.自2020年3月开始,我国生猪、猪肉价格持续上涨,某大型菜场在销售过程中发现,从2020年10月1日起到11月9日的40天内,猪肉的每千克售价与上市时间的关系用图1的一条折线表示:猪肉的进价与上市时间的关系用图2的一段抛物线表示.
(1) ;
(2)求图1表示的售价与时间的函数关系式;
(3)问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低,最低利润为多少?
4. 在平面直角坐标系xOy中,关于x的二次函数y=x2+px+q的图象过点(-1,0),(3,0).
(1)求这个二次函数的解折式;
(2)求当-2≤x≤6时,y的最大值与最小值的差;
(3)一次函数y=(2-m)x+2-m的图象与二次函数y=x2+px+q图象交点的横坐标分别是a和b,且a<3<b,求m的取值范围.
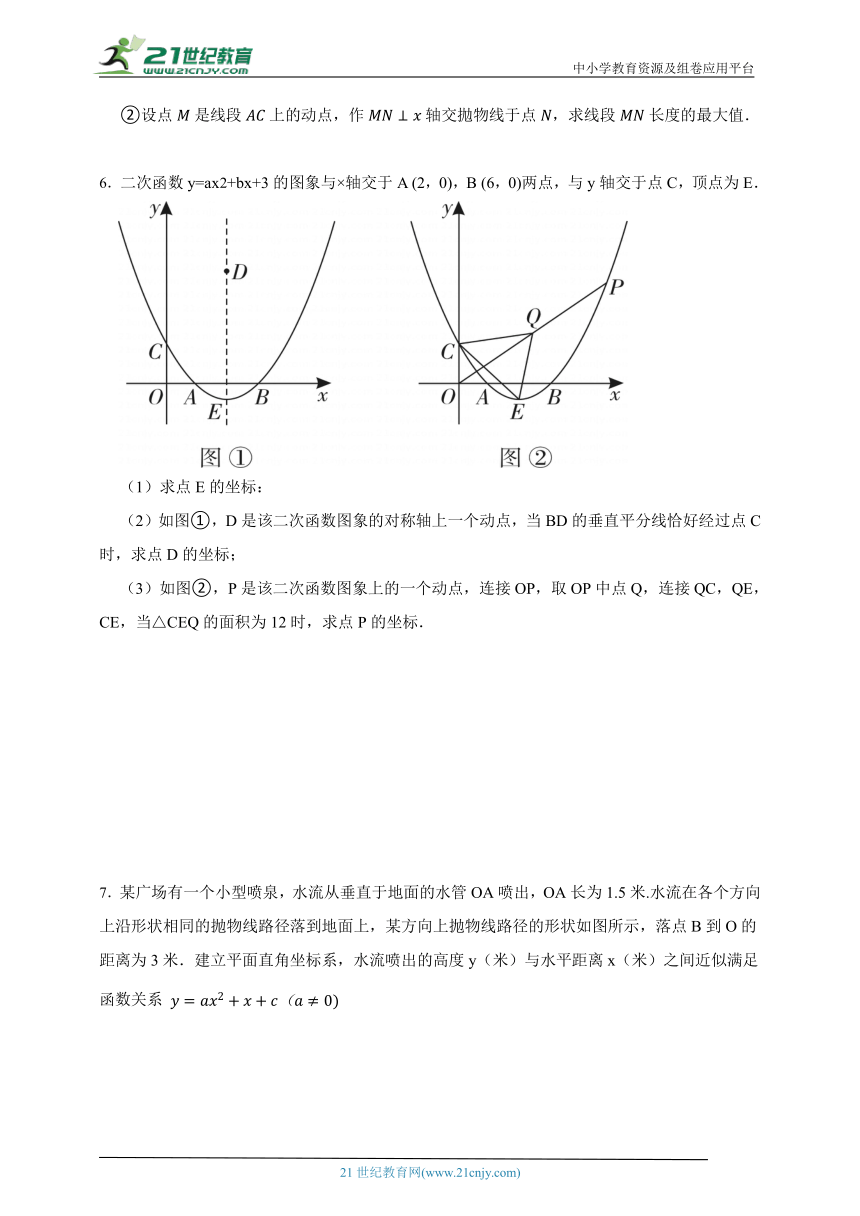
5.如图,抛物线与轴相交于两点,其中点的坐标为点坐标为,且点在抛物线上.
(1)求抛物线的解析式;
(2)点为抛物线与轴的交点;
①点在抛物线上,且,求点坐标;
②设点是线段上的动点,作轴交拋物线于点,求线段长度的最大值.
6.二次函数y=ax2+bx+3的图象与×轴交于A (2,0),B (6,0)两点,与y轴交于点C,顶点为E.
(1)求点E的坐标:
(2)如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;
(3)如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.
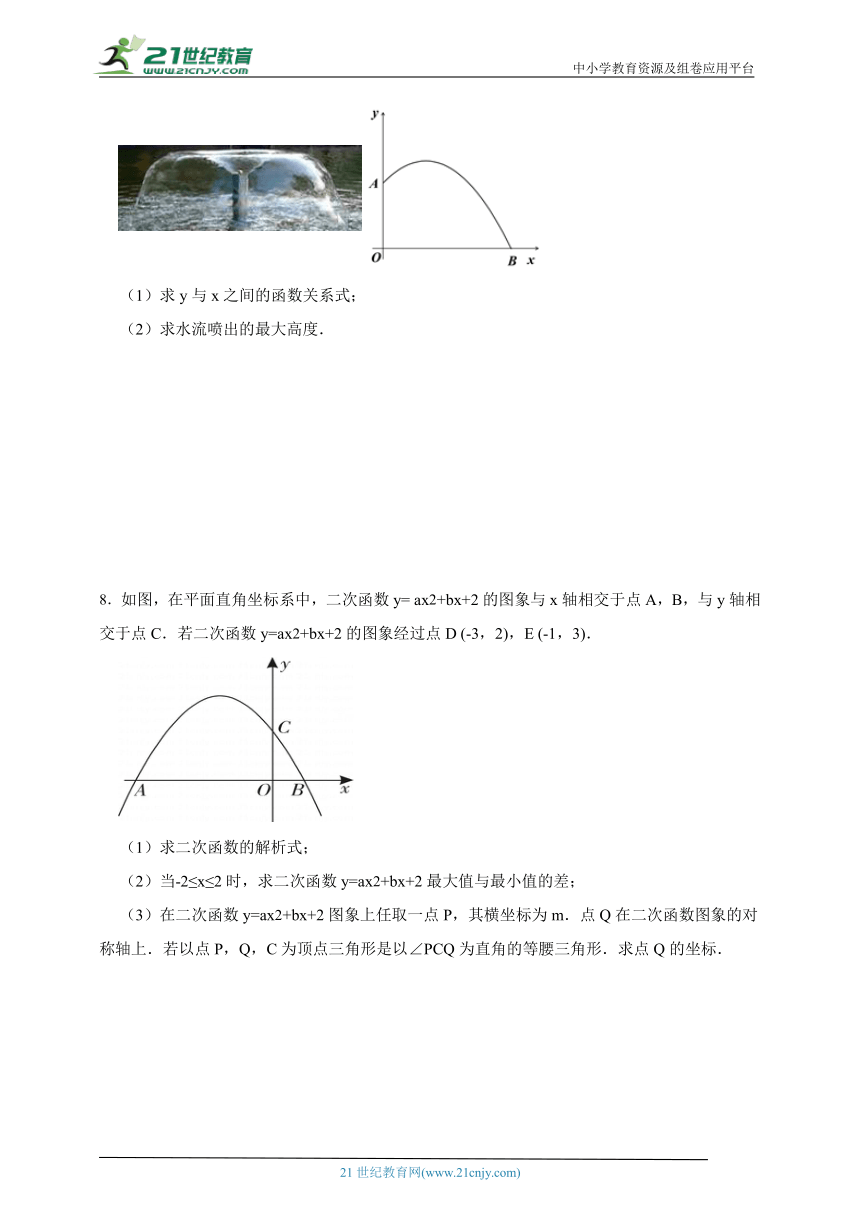
7.某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5米.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3米.建立平面直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间近似满足函数关系
(1)求y与x之间的函数关系式;
(2)求水流喷出的最大高度.
8.如图,在平面直角坐标系中,二次函数y= ax2+bx+2的图象与x轴相交于点A,B,与y轴相交于点C.若二次函数y=ax2+bx+2的图象经过点D (-3,2),E (-1,3).
(1)求二次函数的解析式;
(2)当-2≤x≤2时,求二次函数y=ax2+bx+2最大值与最小值的差;
(3)在二次函数y=ax2+bx+2图象上任取一点P,其横坐标为m.点Q在二次函数图象的对称轴上.若以点P,Q,C为顶点三角形是以∠PCQ为直角的等腰三角形.求点Q的坐标.
9.如图,已知二次函数的图象交轴于点,交轴于点.
(1)求这个二次函数的表达式;
(2)点是直线下方抛物线上的一动点,求面积的最大值;
(3)直线分别交直线和抛物线于点,当是等腰三角形时,求的值.
10.如图,在平面直角坐标系中,直线l与x轴交于点,与y轴交于点,抛物线经过点A,B,且对称轴是直线.
(1)求直线l的解析式;
(2)求抛物线的解析式;
(3)点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C,交直线l于点D,过点P作,垂足为M.求的最大值及此时P点的坐标.
11.如图,抛物线y=-x2+bx十c交x轴于A(-1,0),B两点,交y轴于C(0,3),点P在抛物线上,横坐标设为m.
(1)求抛物线的解析式;
(2)当点P在x轴上方时,直接写出m的取值范围;
(3)当点P到y轴的距离是1时,直接写出△BCP的面积;
(4)若抛物线在点P右侧部分(含点P)的最高点的纵坐标为-1-m,求m的值.
12.如图,抛物线y=ax2+x+c上的点A,C的坐标分别为(0,2),(4,0),抛物线与x轴负半轴交于点B,点M为y轴负半轴上一点,且OM=2,连接AC、CM.
(1)点M的坐标为
(2)求此抛物线的解析式.
(3)点P是抛物线位于第一象限图像上的动点, 连接AP、CP,当S△PAC =S△ACM时,点P的横坐标为
(4)将抛物线沿x轴的负方向平移m(m>0)个单位长度,得到新抛物线,点A的对应点为点A',点C的对应点为点C',在抛物线平移的过程中,
①当点C'在线段A'M上时,m的值为 ▲
②当MA'+MC的值最小时,直接写出m的值.
13.已知:是方程的两个实数根,且,抛物线的图像经过点,,如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与轴的另一交点为,抛物线的顶点为,试求出点的坐标和的面积;
(3)是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为2:3的两部分,请直接写出点的坐标.
14. 如图,为已知抛物线经过,两点,与轴的另一个交点为,顶点为,连结.
(1)求该抛物线的表达式;
(2)点为该抛物线上一动点与点、不重合,设点的横坐标为.
当时,求的值;
该抛物线上是否存在点,使得?若存在,求出所有点的坐标;若不存在,请说明理由.
15. 如图,抛物线的顶点为,与轴的交点为和将抛物线绕点逆时针方向旋转,点,为点,旋转后的对应点,旋转后的抛物线与轴相交于,.
(1)若原抛物线过点,求抛物线的解析式;
(2)若,关于点成中心对称,求直线的解析式;
(3)在的条件下,若点是原抛物线上的一动点,点是旋转后的图形的对称轴上一点,为线段的中点,是否存在点,使得以,,,为顶点的四边形是平行四边形;若存在请求出点坐标,若不存在,请说明理由.
答案解析部分
1.【答案】(1)解:当y=0时,0=﹣ x2+ x+2, 解得:x1=﹣1,x2=4, 则A(﹣1,0),B(4,0), 当x=0时,y=2, 故C(0,2)
(2)解:①过点D作DE⊥x轴于点E, ∵将△ABC绕AB中点M旋转180°,得到△BAD, ∴DE=2,AO=BE=1,OM=ME=1.5, ∴D(3,﹣2); ②∵将△ABC绕AB中点M旋转180°,得到△BAD, ∴AC=BD,AD=BC, ∴四边形ADBC是平行四边形, ∵AC= ,BC= ,AB=5, ∴AC2+BC2=AB2, ∴△ACB是直角三角形, ∴∠ACB=90°, ∴四边形ADBC是矩形
(3)解:由题意可得:BD= ,AD=2 , 则 , 当△BMP∽△ADB时, , 可得:BM=2.5, 则PM=1.25, 故P(1.5,1.25), 当△BMP1∽△ABD时, P1(1.5,﹣1.25), 当△BMP2∽△BDA时, 可得:P2(1.5,5), 当△BMP3∽△BDA时, 可得:P3(1.5,﹣5), 综上所述:点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5).
2.【答案】(1)解:抛物线经过点,,
,解得,
抛物线的解析式为
(2)解:,
抛物线的对称轴为直线,,
四边形是平行四边形,
,
点的横坐标为,
抛物线,当时,,
点的坐标是.
(3)解:存在点,使是直角三角形,
当时,设交于点,作轴于点,
,,,
,
轴,,
,
四边形是平行四边形,
,,
,
,
;
当时,作交的延长线于点,则,
,
∽,
,
设,则,
,,
,
解得,
,
综上所述,存在点,使是直角三角形,点的坐标为或
3.【答案】(1)
(2)解:当0≤x<30时,设P=kx+b,
∴
解之:
∴p=2x+60;
当30≤x≤40时,设p=mx+n
解之:
∴p=-2x+180
∴
(3)解:设利润为W,
当0≤x<30时,
,
∵抛物线的开口向上,
∴当x=20时W的最小值为10;
当30≤x≤40时
,
∵抛物线的开口向上,
∴当x=40时W的最小值为10;
∴当20天或40天,最小利润为10元 / 千克
4.【答案】(1)解:由二次函数y=x2+px+q的图象过点(-1,0),(3,0).
∴y=(x+1)(x-3),
∴此二次函数的表达式为y=x2-2x-3;
(2)解:∵抛物线开口向上,对称轴为直线,
∴在范围内,当x=6,函数有最大值为:;当x=1时函数有最小值:,
∴y的最大值与最小值的差为:21-(-4)=25;
(3)解:y=(2-m)x+2-m与二次函数y=x2-2x-3图象交点的横坐标为a和b,
∴x2-2x-3=(2-m)x+2-m,整理得x2+(m-4)x+m-5=0,
解得:,
∵a<3<b,
∴a=-1,b=5-m>3,
解得m<2,即m的取值范围是m<2 .
5.【答案】(1)解:∵抛物线与轴相交于,,
∴设解析式为,
将代入中,得,
解得:,
所以抛物线的解析式为:.
(2)解:①二次函数的解析式为,
抛物线与轴的交点的坐标为,.
设点坐标为,
,
,
,.
当时,;
当时,.
点的坐标为或;
②
设直线的解析式为,将,代入,
得,
解得:.
即直线的解析式为.
设点坐标为,,则点坐标为,
,
当时,有最大值.
6.【答案】(1)解:将A (2,0), B (6, 0)代入y=ax2+ bx+3,
得
解得
∴二次函数的解析式为y=x2-2x+3.
∴y=x2-2x+3=(x-4)2-1,
∴E(4,-1);
(2)解:如图1,图2,连接CB,CD,由点C在线段BD的垂直平分线CN上,得CB=CD.
设D(4,m),
∵C(0,3),由勾股定理可得:
42+ (m-3)2=62+32.
解得m=3±
∴满足条件的点D的坐标为(4,3+)或(4,3-);
(3)
解:如图3,设CQ交抛物线的对称轴于点M,
设P (n,n2-2n+3),则Q(n,n2-n+,)
设直线CQ的解析式为y=k×+3,则n2-n+=nk+3.
解得k=n-2-,于是CQ:y= (n-2-)x+3,
当×=4时,y=4 (n-2-)+3=n-5-
M(4,n-5-), ME=n-4-.
∵S△CQE= S△CEM+S△QEM
=·n·(n-4-)
=12.
∴n2-4n- 60=0,
解得n=10或n=-6,
当n=10时,P (10,8),当n=-6时,P(-6,24).
综合以上可得,满足条件的点P的坐标为(10,8)或(-6,24).
7.【答案】(1)解:由题意可得,
抛物线经过(0,1.5)和(3,0),
解得:a=-0.5,c=1.5,
即函数表达式为y= .
(2)解:
∴当x=1时,y取得最大值,此时y=2.
答:水流喷出的最大高度为2米.
8.【答案】(1)将D (-3, 2),E (-1, 3)代入y=ax2+bx+2,
∴
解得
∴y=x2x+2
(2)∵y=x2x+2=
∴抛物线的对称轴为直线x=
当-2≤x≤2时,函数的最大值为,最小值为-3,∴函数的最大值与最小值的差为
(3)∵P 点横坐标为m,
∴P (m,m2m+2)
当x=0时,y=2,
∴C (0, 2),
当P点在y轴左侧时,
过点P作PN⊥y轴交于点N,过点Q作QM⊥y轴交于点M,
∵∠PCQ=90° ,
∴∠QCM+∠PCN=90°,
∵∠CQM+∠QCM= =90° ,
∴∠CQM=∠PCN,
∵CQ=PC,
∴△CQM≌△PCN (AAS),
∴QM=CN=m2m,CM=PN=-m,
∴m2m=
解得m=
∵m<0,
∴m=
∴n=2+=.
∴Q (,);
当P点在y轴右侧时,
过点C作GH⊥y轴,过点P作PH⊥GH交于H点,过点2作GQ⊥GH交于G点,
同理可得△CQG≌△PCH (AAS), .
∴CG=PH=,GQ=CH=m,
∴m2+m=
解得m=
∵m<0,
∴m=
∴n=2-=.
∴Q (,);
综上所述: Q点坐标为(,)或(,)
9.【答案】(1)解:将代入函数表达式,得
解得
这个二次函数的表达式是;
(2)解:当时,,即点,
设直线的表达式为,将点,点代入得解得
直线的表达式为,
过点作轴,交直线于点.
设点坐标为,
点坐标为,
,
,
,
当时,最大,最大值为;
(3)解:由题意得,,,
当时,
①,解得,
②,解得,
当时,,点与点重合,
;
当时,,
,解得或(舍),
当是等腰三角形时,的值为.
10.【答案】(1)解:设直线l的解析式为()
把A,B两点的坐标代入解析式,得,解得
∴直线l的解析式为;
(2)解:设抛物线的解析式为()
∵抛物线的对称轴为直线
∴
把A,B两点坐标代入解析式,得解得
∴抛物线的解析式为;
(3)解:∵,,
∴
在中
∴
∵轴,
∴
在中
∵,
∴
∴
在中,
∴
∴
∵
∴设点P的坐标为
∴
∴
∵
∴当时,有最大值是,此时最大
当时
∴
∴的最大值是,此时的P点坐标是.
11.【答案】(1)解:将点A(-1,0),C(0,3)代入抛物线解析式得:
解得:
则抛物线的解析式为y=-x2+2x十3
(2)-1(3)6或3
(4)解:当m≤1时
若抛物线再点P右侧部分(含点P)的最高点的纵坐标为-1-m
则顶点的纵坐标为-1-m,即4=-1-m
解得:m=-5
当m>1时,则抛物线在x=m处取得最大值
即-1-m=-m2+2m+3
解得:m=-1(舍去)或4
故答案为:m=-5或4
12.【答案】(1)(0,-2)
(2)解:根据题意,得
解得
所以抛物线的解析式为y= -x2+x+2.
(3)2
(4)①8
②
13.【答案】(1)解:解方程,得,.
由,有,.
所以点A,B的坐标分别为,.
将,的坐标分别代入,
得解这个方程组,得
所以抛物线的解析式为.
(2)解:由,令,得.
解这个方程,得,.
所以点C的坐标为,由顶点坐标公式计算,得点.
过D作轴的垂线交轴于,如图所示.
则.
,.
所以
(3)或
14.【答案】(1)解:将点、坐标代入二次函数表达式得:,
解得:,
故抛物线的表达式为:,
令,则或,
即点;
(2)解:如图,过点作轴的平行线交于点,
将点、的坐标代入一次函数表达式并解得:
直线的表达式为:,
设点,则点,
,
或,
解得或或或;
设直线与交于点,
当点在直线下方时,
,
点在的中垂线上,
线段的中点坐标为,
过该点与垂直的直线的值为,
设中垂线的表达式为:,将点代入上式并解得:直线中垂线的表达式为:,
同理直线的表达式为:,
联立并解得:,即点,
同理可得直线的表达式为:,
联立并解得:或舍去,
故点;
当点在直线上方时,
,
,
则直线的表达式为:,将点坐标代入上式并解得:,
即直线的表达式为:,
联立并解得:或舍去,
故点;
故点的坐标为或.
15.【答案】(1)解:由抛物线的顶点为,设抛物线的解析式为,
把代入得:
,
解得,
;
抛物线的解析式为;
(2)解:连接,设抛物线对称轴交轴于,如图:
将抛物线绕点逆时针方向旋转,点,为点,旋转后的对应点,
,,
,
,关于点成中心对称,
是的中点,即在线段上,
,
,
,
,
,
,
,
设直线解析式为,
将,代入得:
,
解得,
直线解析式为;
(3)解:存在点,使得以,,,为顶点的四边形是平行四边形,理由如下:
由知,
把代入得:,
解得,
原抛物线解析式为;
,关于直线对称,
,
,为线段的中点,
,
把原抛物线的对称轴直线绕逆时针方向旋转得直线,
设,,
而,,
若,为对角线,则,的中点重合,
,
解得或;
或;
若,为对角线,
,
方程组无实数解;
若,为对角线,
,
解得或,
或;
综上所述,的坐标为或或或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学九年级下册北师大版第二章二次函数压轴题特训
1.如图,抛物线y=﹣ x2+ x+2与x轴交于点A,B,与y轴交于点C.
(1)试求A,B,C的坐标;
(2)将△ABC绕AB中点M旋转180°,得到△BAD.
①求点D的坐标;
②判断四边形ADBC的形状,并说明理由;
(3)在该抛物线对称轴上是否存在点P,使△BMP与△BAD相似?若存在,请直接写出所有满足条件的P点的坐标;若不存在,请说明理由.
2.如图,抛物线与轴交于点和.
(1)求抛物线的解析式;
(2)抛物线的对称轴交轴于点,点是位于轴上方对称轴上一点,轴,与对称轴右侧的抛物线交于点,四边形是平行四边形,求点的坐标;
(3)在的条件下,连接,轴上方的对称轴上是否存在点,使是直角三角形?若存在,求出点的坐标;若不存在,请说明理由.
3.自2020年3月开始,我国生猪、猪肉价格持续上涨,某大型菜场在销售过程中发现,从2020年10月1日起到11月9日的40天内,猪肉的每千克售价与上市时间的关系用图1的一条折线表示:猪肉的进价与上市时间的关系用图2的一段抛物线表示.
(1) ;
(2)求图1表示的售价与时间的函数关系式;
(3)问从10月1日起到11月9日的40天内第几天每千克猪肉利润最低,最低利润为多少?
4. 在平面直角坐标系xOy中,关于x的二次函数y=x2+px+q的图象过点(-1,0),(3,0).
(1)求这个二次函数的解折式;
(2)求当-2≤x≤6时,y的最大值与最小值的差;
(3)一次函数y=(2-m)x+2-m的图象与二次函数y=x2+px+q图象交点的横坐标分别是a和b,且a<3<b,求m的取值范围.
5.如图,抛物线与轴相交于两点,其中点的坐标为点坐标为,且点在抛物线上.
(1)求抛物线的解析式;
(2)点为抛物线与轴的交点;
①点在抛物线上,且,求点坐标;
②设点是线段上的动点,作轴交拋物线于点,求线段长度的最大值.
6.二次函数y=ax2+bx+3的图象与×轴交于A (2,0),B (6,0)两点,与y轴交于点C,顶点为E.
(1)求点E的坐标:
(2)如图①,D是该二次函数图象的对称轴上一个动点,当BD的垂直平分线恰好经过点C时,求点D的坐标;
(3)如图②,P是该二次函数图象上的一个动点,连接OP,取OP中点Q,连接QC,QE,CE,当△CEQ的面积为12时,求点P的坐标.
7.某广场有一个小型喷泉,水流从垂直于地面的水管OA喷出,OA长为1.5米.水流在各个方向上沿形状相同的抛物线路径落到地面上,某方向上抛物线路径的形状如图所示,落点B到O的距离为3米.建立平面直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间近似满足函数关系
(1)求y与x之间的函数关系式;
(2)求水流喷出的最大高度.
8.如图,在平面直角坐标系中,二次函数y= ax2+bx+2的图象与x轴相交于点A,B,与y轴相交于点C.若二次函数y=ax2+bx+2的图象经过点D (-3,2),E (-1,3).
(1)求二次函数的解析式;
(2)当-2≤x≤2时,求二次函数y=ax2+bx+2最大值与最小值的差;
(3)在二次函数y=ax2+bx+2图象上任取一点P,其横坐标为m.点Q在二次函数图象的对称轴上.若以点P,Q,C为顶点三角形是以∠PCQ为直角的等腰三角形.求点Q的坐标.
9.如图,已知二次函数的图象交轴于点,交轴于点.
(1)求这个二次函数的表达式;
(2)点是直线下方抛物线上的一动点,求面积的最大值;
(3)直线分别交直线和抛物线于点,当是等腰三角形时,求的值.
10.如图,在平面直角坐标系中,直线l与x轴交于点,与y轴交于点,抛物线经过点A,B,且对称轴是直线.
(1)求直线l的解析式;
(2)求抛物线的解析式;
(3)点P是直线l下方抛物线上的一动点,过点P作轴,垂足为C,交直线l于点D,过点P作,垂足为M.求的最大值及此时P点的坐标.
11.如图,抛物线y=-x2+bx十c交x轴于A(-1,0),B两点,交y轴于C(0,3),点P在抛物线上,横坐标设为m.
(1)求抛物线的解析式;
(2)当点P在x轴上方时,直接写出m的取值范围;
(3)当点P到y轴的距离是1时,直接写出△BCP的面积;
(4)若抛物线在点P右侧部分(含点P)的最高点的纵坐标为-1-m,求m的值.
12.如图,抛物线y=ax2+x+c上的点A,C的坐标分别为(0,2),(4,0),抛物线与x轴负半轴交于点B,点M为y轴负半轴上一点,且OM=2,连接AC、CM.
(1)点M的坐标为
(2)求此抛物线的解析式.
(3)点P是抛物线位于第一象限图像上的动点, 连接AP、CP,当S△PAC =S△ACM时,点P的横坐标为
(4)将抛物线沿x轴的负方向平移m(m>0)个单位长度,得到新抛物线,点A的对应点为点A',点C的对应点为点C',在抛物线平移的过程中,
①当点C'在线段A'M上时,m的值为 ▲
②当MA'+MC的值最小时,直接写出m的值.
13.已知:是方程的两个实数根,且,抛物线的图像经过点,,如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与轴的另一交点为,抛物线的顶点为,试求出点的坐标和的面积;
(3)是线段上的一点,过点作轴,与抛物线交于点,若直线把分成面积之比为2:3的两部分,请直接写出点的坐标.
14. 如图,为已知抛物线经过,两点,与轴的另一个交点为,顶点为,连结.
(1)求该抛物线的表达式;
(2)点为该抛物线上一动点与点、不重合,设点的横坐标为.
当时,求的值;
该抛物线上是否存在点,使得?若存在,求出所有点的坐标;若不存在,请说明理由.
15. 如图,抛物线的顶点为,与轴的交点为和将抛物线绕点逆时针方向旋转,点,为点,旋转后的对应点,旋转后的抛物线与轴相交于,.
(1)若原抛物线过点,求抛物线的解析式;
(2)若,关于点成中心对称,求直线的解析式;
(3)在的条件下,若点是原抛物线上的一动点,点是旋转后的图形的对称轴上一点,为线段的中点,是否存在点,使得以,,,为顶点的四边形是平行四边形;若存在请求出点坐标,若不存在,请说明理由.
答案解析部分
1.【答案】(1)解:当y=0时,0=﹣ x2+ x+2, 解得:x1=﹣1,x2=4, 则A(﹣1,0),B(4,0), 当x=0时,y=2, 故C(0,2)
(2)解:①过点D作DE⊥x轴于点E, ∵将△ABC绕AB中点M旋转180°,得到△BAD, ∴DE=2,AO=BE=1,OM=ME=1.5, ∴D(3,﹣2); ②∵将△ABC绕AB中点M旋转180°,得到△BAD, ∴AC=BD,AD=BC, ∴四边形ADBC是平行四边形, ∵AC= ,BC= ,AB=5, ∴AC2+BC2=AB2, ∴△ACB是直角三角形, ∴∠ACB=90°, ∴四边形ADBC是矩形
(3)解:由题意可得:BD= ,AD=2 , 则 , 当△BMP∽△ADB时, , 可得:BM=2.5, 则PM=1.25, 故P(1.5,1.25), 当△BMP1∽△ABD时, P1(1.5,﹣1.25), 当△BMP2∽△BDA时, 可得:P2(1.5,5), 当△BMP3∽△BDA时, 可得:P3(1.5,﹣5), 综上所述:点P的坐标为:(1.5,1.25),(1.5,﹣1.25),(1.5,5),(1.5,﹣5).
2.【答案】(1)解:抛物线经过点,,
,解得,
抛物线的解析式为
(2)解:,
抛物线的对称轴为直线,,
四边形是平行四边形,
,
点的横坐标为,
抛物线,当时,,
点的坐标是.
(3)解:存在点,使是直角三角形,
当时,设交于点,作轴于点,
,,,
,
轴,,
,
四边形是平行四边形,
,,
,
,
;
当时,作交的延长线于点,则,
,
∽,
,
设,则,
,,
,
解得,
,
综上所述,存在点,使是直角三角形,点的坐标为或
3.【答案】(1)
(2)解:当0≤x<30时,设P=kx+b,
∴
解之:
∴p=2x+60;
当30≤x≤40时,设p=mx+n
解之:
∴p=-2x+180
∴
(3)解:设利润为W,
当0≤x<30时,
,
∵抛物线的开口向上,
∴当x=20时W的最小值为10;
当30≤x≤40时
,
∵抛物线的开口向上,
∴当x=40时W的最小值为10;
∴当20天或40天,最小利润为10元 / 千克
4.【答案】(1)解:由二次函数y=x2+px+q的图象过点(-1,0),(3,0).
∴y=(x+1)(x-3),
∴此二次函数的表达式为y=x2-2x-3;
(2)解:∵抛物线开口向上,对称轴为直线,
∴在范围内,当x=6,函数有最大值为:;当x=1时函数有最小值:,
∴y的最大值与最小值的差为:21-(-4)=25;
(3)解:y=(2-m)x+2-m与二次函数y=x2-2x-3图象交点的横坐标为a和b,
∴x2-2x-3=(2-m)x+2-m,整理得x2+(m-4)x+m-5=0,
解得:,
∵a<3<b,
∴a=-1,b=5-m>3,
解得m<2,即m的取值范围是m<2 .
5.【答案】(1)解:∵抛物线与轴相交于,,
∴设解析式为,
将代入中,得,
解得:,
所以抛物线的解析式为:.
(2)解:①二次函数的解析式为,
抛物线与轴的交点的坐标为,.
设点坐标为,
,
,
,.
当时,;
当时,.
点的坐标为或;
②
设直线的解析式为,将,代入,
得,
解得:.
即直线的解析式为.
设点坐标为,,则点坐标为,
,
当时,有最大值.
6.【答案】(1)解:将A (2,0), B (6, 0)代入y=ax2+ bx+3,
得
解得
∴二次函数的解析式为y=x2-2x+3.
∴y=x2-2x+3=(x-4)2-1,
∴E(4,-1);
(2)解:如图1,图2,连接CB,CD,由点C在线段BD的垂直平分线CN上,得CB=CD.
设D(4,m),
∵C(0,3),由勾股定理可得:
42+ (m-3)2=62+32.
解得m=3±
∴满足条件的点D的坐标为(4,3+)或(4,3-);
(3)
解:如图3,设CQ交抛物线的对称轴于点M,
设P (n,n2-2n+3),则Q(n,n2-n+,)
设直线CQ的解析式为y=k×+3,则n2-n+=nk+3.
解得k=n-2-,于是CQ:y= (n-2-)x+3,
当×=4时,y=4 (n-2-)+3=n-5-
M(4,n-5-), ME=n-4-.
∵S△CQE= S△CEM+S△QEM
=·n·(n-4-)
=12.
∴n2-4n- 60=0,
解得n=10或n=-6,
当n=10时,P (10,8),当n=-6时,P(-6,24).
综合以上可得,满足条件的点P的坐标为(10,8)或(-6,24).
7.【答案】(1)解:由题意可得,
抛物线经过(0,1.5)和(3,0),
解得:a=-0.5,c=1.5,
即函数表达式为y= .
(2)解:
∴当x=1时,y取得最大值,此时y=2.
答:水流喷出的最大高度为2米.
8.【答案】(1)将D (-3, 2),E (-1, 3)代入y=ax2+bx+2,
∴
解得
∴y=x2x+2
(2)∵y=x2x+2=
∴抛物线的对称轴为直线x=
当-2≤x≤2时,函数的最大值为,最小值为-3,∴函数的最大值与最小值的差为
(3)∵P 点横坐标为m,
∴P (m,m2m+2)
当x=0时,y=2,
∴C (0, 2),
当P点在y轴左侧时,
过点P作PN⊥y轴交于点N,过点Q作QM⊥y轴交于点M,
∵∠PCQ=90° ,
∴∠QCM+∠PCN=90°,
∵∠CQM+∠QCM= =90° ,
∴∠CQM=∠PCN,
∵CQ=PC,
∴△CQM≌△PCN (AAS),
∴QM=CN=m2m,CM=PN=-m,
∴m2m=
解得m=
∵m<0,
∴m=
∴n=2+=.
∴Q (,);
当P点在y轴右侧时,
过点C作GH⊥y轴,过点P作PH⊥GH交于H点,过点2作GQ⊥GH交于G点,
同理可得△CQG≌△PCH (AAS), .
∴CG=PH=,GQ=CH=m,
∴m2+m=
解得m=
∵m<0,
∴m=
∴n=2-=.
∴Q (,);
综上所述: Q点坐标为(,)或(,)
9.【答案】(1)解:将代入函数表达式,得
解得
这个二次函数的表达式是;
(2)解:当时,,即点,
设直线的表达式为,将点,点代入得解得
直线的表达式为,
过点作轴,交直线于点.
设点坐标为,
点坐标为,
,
,
,
当时,最大,最大值为;
(3)解:由题意得,,,
当时,
①,解得,
②,解得,
当时,,点与点重合,
;
当时,,
,解得或(舍),
当是等腰三角形时,的值为.
10.【答案】(1)解:设直线l的解析式为()
把A,B两点的坐标代入解析式,得,解得
∴直线l的解析式为;
(2)解:设抛物线的解析式为()
∵抛物线的对称轴为直线
∴
把A,B两点坐标代入解析式,得解得
∴抛物线的解析式为;
(3)解:∵,,
∴
在中
∴
∵轴,
∴
在中
∵,
∴
∴
在中,
∴
∴
∵
∴设点P的坐标为
∴
∴
∵
∴当时,有最大值是,此时最大
当时
∴
∴的最大值是,此时的P点坐标是.
11.【答案】(1)解:将点A(-1,0),C(0,3)代入抛物线解析式得:
解得:
则抛物线的解析式为y=-x2+2x十3
(2)-1
(4)解:当m≤1时
若抛物线再点P右侧部分(含点P)的最高点的纵坐标为-1-m
则顶点的纵坐标为-1-m,即4=-1-m
解得:m=-5
当m>1时,则抛物线在x=m处取得最大值
即-1-m=-m2+2m+3
解得:m=-1(舍去)或4
故答案为:m=-5或4
12.【答案】(1)(0,-2)
(2)解:根据题意,得
解得
所以抛物线的解析式为y= -x2+x+2.
(3)2
(4)①8
②
13.【答案】(1)解:解方程,得,.
由,有,.
所以点A,B的坐标分别为,.
将,的坐标分别代入,
得解这个方程组,得
所以抛物线的解析式为.
(2)解:由,令,得.
解这个方程,得,.
所以点C的坐标为,由顶点坐标公式计算,得点.
过D作轴的垂线交轴于,如图所示.
则.
,.
所以
(3)或
14.【答案】(1)解:将点、坐标代入二次函数表达式得:,
解得:,
故抛物线的表达式为:,
令,则或,
即点;
(2)解:如图,过点作轴的平行线交于点,
将点、的坐标代入一次函数表达式并解得:
直线的表达式为:,
设点,则点,
,
或,
解得或或或;
设直线与交于点,
当点在直线下方时,
,
点在的中垂线上,
线段的中点坐标为,
过该点与垂直的直线的值为,
设中垂线的表达式为:,将点代入上式并解得:直线中垂线的表达式为:,
同理直线的表达式为:,
联立并解得:,即点,
同理可得直线的表达式为:,
联立并解得:或舍去,
故点;
当点在直线上方时,
,
,
则直线的表达式为:,将点坐标代入上式并解得:,
即直线的表达式为:,
联立并解得:或舍去,
故点;
故点的坐标为或.
15.【答案】(1)解:由抛物线的顶点为,设抛物线的解析式为,
把代入得:
,
解得,
;
抛物线的解析式为;
(2)解:连接,设抛物线对称轴交轴于,如图:
将抛物线绕点逆时针方向旋转,点,为点,旋转后的对应点,
,,
,
,关于点成中心对称,
是的中点,即在线段上,
,
,
,
,
,
,
,
设直线解析式为,
将,代入得:
,
解得,
直线解析式为;
(3)解:存在点,使得以,,,为顶点的四边形是平行四边形,理由如下:
由知,
把代入得:,
解得,
原抛物线解析式为;
,关于直线对称,
,
,为线段的中点,
,
把原抛物线的对称轴直线绕逆时针方向旋转得直线,
设,,
而,,
若,为对角线,则,的中点重合,
,
解得或;
或;
若,为对角线,
,
方程组无实数解;
若,为对角线,
,
解得或,
或;
综上所述,的坐标为或或或
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
