第6章 图形的相似压轴题特训（含解析）

中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册苏科版第6章图形的相似压轴题特训
1．如图，Rt△ABC中，∠ACB＝90°，AC＝6cm，BC＝8cm．动点M从点B出发，在BA边上以每秒3cm的速度向定点A运动，同时动点N从点C出发，在CB边上以每秒2cm的速度向点B运动，且MG⊥BC，运动时间为t秒（0＜t＜ ），连接MN．
（1）用含t的式子表示MG；
（2）当t为何值时，四边形ACNM的面积最小？并求出最小面积；
（3）若△BMN与△ABC相似，求t的值．
2．如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C.
（1）求证：△ABD∽△ACB
（2）若AB=6，AD=4，求线段CD的长
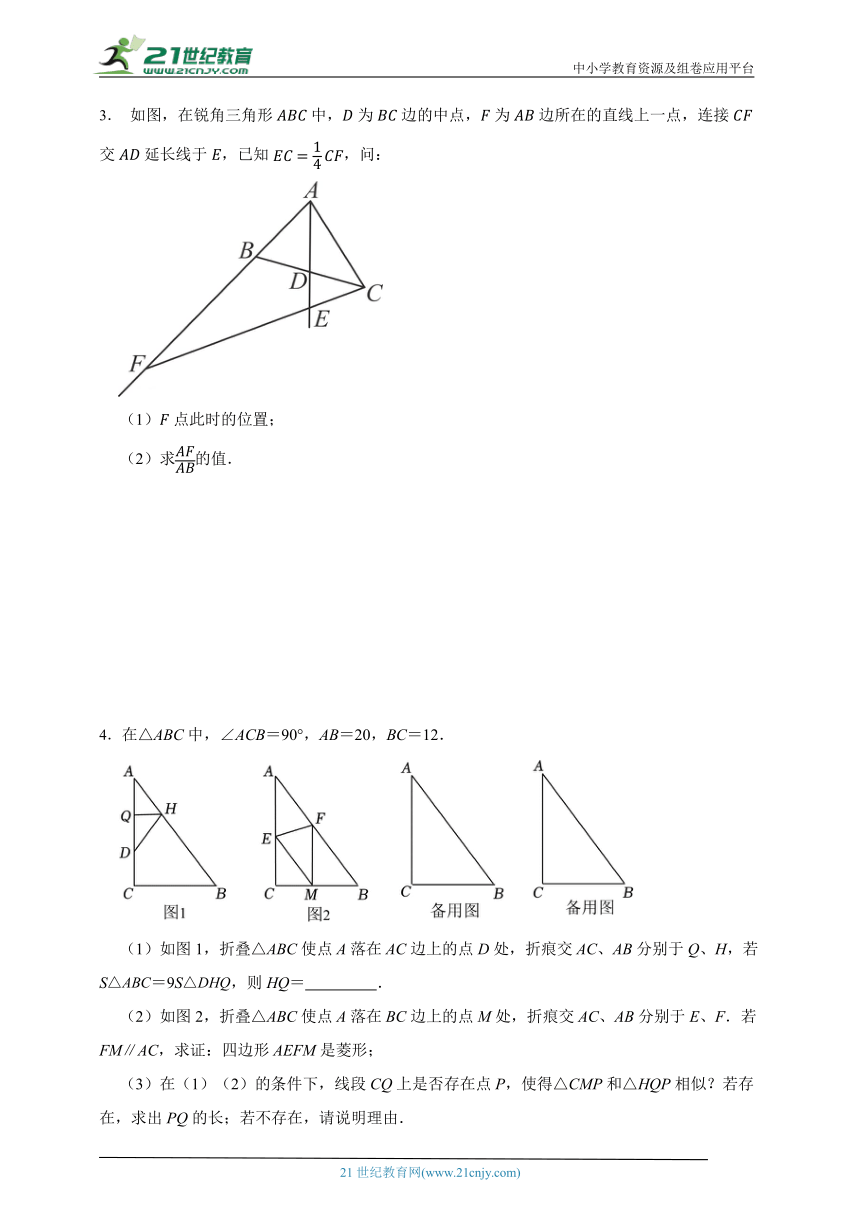
3． 如图，在锐角三角形中，为边的中点，为边所在的直线上一点，连接交延长线于，已知，问：
（1）点此时的位置；
（2）求的值．
4．在△ABC中，∠ACB＝90°，AB＝20，BC＝12．
（1）如图1，折叠△ABC使点A落在AC边上的点D处，折痕交AC、AB分别于Q、H，若S△ABC＝9S△DHQ，则HQ＝　 　．
（2）如图2，折叠△ABC使点A落在BC边上的点M处，折痕交AC、AB分别于E、F．若FM∥AC，求证：四边形AEFM是菱形；
（3）在（1）（2）的条件下，线段CQ上是否存在点P，使得△CMP和△HQP相似？若存在，求出PQ的长；若不存在，请说明理由．
（4）在线段AC上找一点G，使值最小，请直接写出最小值．
5．如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处．点E到地面的高度DE＝3.5m，点F到地面的高度CF＝1.5m，灯泡到木板的水平距离AC＝5.4m，墙到木板的水平距离为CD＝4m．已知光在镜面反射中的入射角等于反射角，图中点A、B、C、D在同一水平面上．
（1）求BC的长．
（2）求灯泡到地面的高度AG．
6． 已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90°，点A、C的坐标分别为A(-3，0)．C(1，0)，
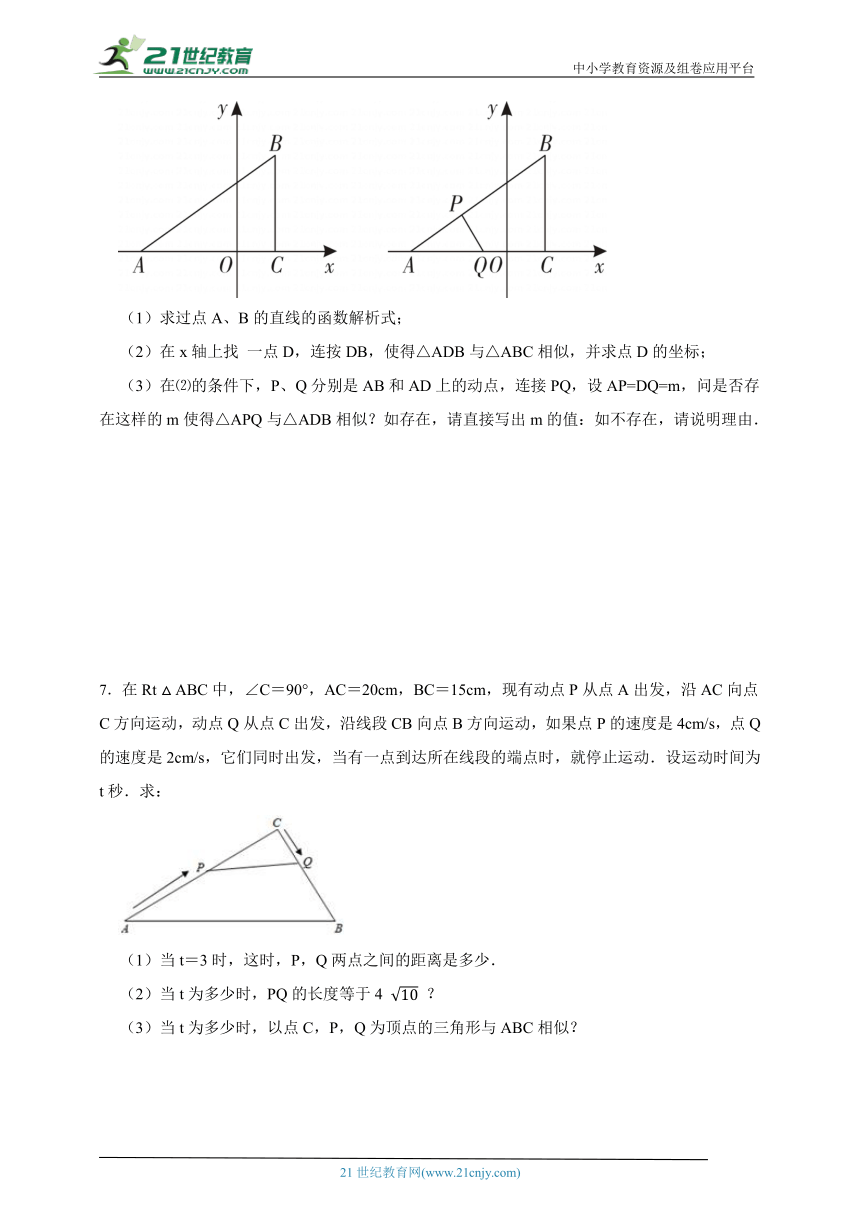
（1）求过点A、B的直线的函数解析式；
（2）在x轴上找 一点D，连按DB，使得△ADB与△ABC相似，并求点D的坐标；
（3）在⑵的条件下，P、Q分别是AB和AD上的动点，连接PQ，设AP=DQ=m，问是否存在这样的m使得△APQ与△ADB相似？如存在，请直接写出m的值：如不存在，请说明理由．
7．在Rt ABC中，∠C＝90°，AC＝20cm，BC＝15cm，现有动点P从点A出发，沿AC向点C方向运动，动点Q从点C出发，沿线段CB向点B方向运动，如果点P的速度是4cm/s，点Q的速度是2cm/s，它们同时出发，当有一点到达所在线段的端点时，就停止运动．设运动时间为t秒．求：
（1）当t＝3时，这时，P，Q两点之间的距离是多少．
（2）当t为多少时，PQ的长度等于4 ？
（3）当t为多少时，以点C，P，Q为顶点的三角形与ABC相似？
8．如图，在中，，，动点从点出发，沿以每秒个单位长度的速度向终点运动，当点不与点重合时，过点作于点、，过点作，与交于点设点的运动时间为秒．
（1）线段的长为　 　；用含的代数式表示
（2）当点落在边上时，求的值；
（3）当直线将的面积分成：的两部分时，求的值；
（4）当点落在的角平分线上时，直接写出的值．
9．如图，在矩形ABCD中，AB＝3cm，BC＝6cm．点P从点D出发向点A运动，运动到点A即停止；同时，点Q从点B出发向点C运动，运动到点C即停止，点P、Q的速度都是1cm/s．连接PQ、AQ、CP．设点P、Q运动的时间为ts．
（1）当t＝　 　时，四边形ABQP是矩形；
（2）当t＝　 　时，四边形AQCP是菱形；
（3）是否存在某一时刻t使得PQ⊥PC，如果存在，请求出t的值，如果不存在，请说明理由．
（4）在运动过程中，沿着AQ把△ABQ翻折，当t为何值时，翻折后点B的对应点恰好落在PQ边上。
10．如图1，点为矩形ABCD的对称中心，，点为AD边上一点，连结EO并延长，交BC于点.四边形ABFE与关于EF所在直线成轴对称，线段交AD边于点。
（1）求证：.
（2）当时，求AE的长.
（3）令AE=a，DG=b.
①求证：(4-a)(4-b)=4.
②如图2，连结，分别交于点H，K.记四边形OKGH的面积为，的面积为.当时，求的值.
11．在正方形中，、分别为边上的两点，连接、并延长交于点，连接，为上一点，连接、．
（1）如图，若为的中点，且，，求线段的长；
（2）如图，过点作，且，连接，刚好交的中点，当时，求证：；
（3）如图，在的条件下，点为线段上一动点，连接，作于点，将沿翻折得到，点、分别为线段、上两点，且，，连接、交于点，连接，请直接写出面积的最大值．
12．
（1）如图，正方形中，点为边上一点，连接，过点作交边于点，将沿直线折叠后，点落在点处，连接，当点恰好落在上时，求的值；
（2）在的条件下，如图，若把正方形改成菱形，且，，其他条件不变，请求出的值；
13．已知正方形，，是对角线上任意一点．
（1）如图，以为边向右作等腰直角三角形，，连接，则和的数量关系是　 　 ；
（2）如图，点在上，，，求的长为多少；
（3）为上任意一点不与，重合，作于，连接，为上一点，且，当点从点运动到点时，写出点运动的路径的长．
答案解析部分
1．【答案】（1）解：由运动知，BM＝3t，
在Rt△ABC中，AC＝6，BC＝8，
∴AB＝10，
∵MG⊥BC，
∴∠MGB＝90°＝∠ACB，
∵∠B＝∠B，
∴△BGM∽△BCA，
∴ ，
∴ ，
∴MG＝ t
（2）解：由运动知，CN＝2t，
∴BN＝BC﹣CN＝8﹣2t，
由（1）知，MG＝ t，
∴S四边形ACNM＝S△ABC﹣S△BNM＝ BC×AC﹣ BN×MG＝ ×8×6﹣ （8﹣2t）× t＝ （t﹣2）2+ ，
∵0＜t＜ ，
∴t＝2秒时，S四边形ACNM最小＝ cm2
（3）解：由（1）（2）知，BM＝3t，BN＝8﹣2t，
∵△BMN与△ABC相似，
∴①当△BMN∽△BAC时， ，
∴ ，
∴t＝ 秒，
②当△BMN∽△BCA时， ，
∴ ，
∴t＝ 秒，
即：△BMN与△ABC相似，t的值为 秒或 秒
2．【答案】（1）证明：在△ABD和△ACB中，∠ABD=∠C，∠A=∠A，
∴△ABD∽△ACB
（2）解：∵ △ABD∽△ACB，
∴ ，
∵AB=6，AD=4，
∴AC=9，
则CD=AC﹣AD=9﹣4=5.
3．【答案】（1）解：如图，过点作，交于点．
，
．
为的中点，，
，
，
点在的延长线上，且．
（2）解：．
4．【答案】（1）4
（2）解：证明：由题意得△AEF≌△MEF，
∴AE＝AF，ME＝MF，∠AFE＝∠MFE，
∵FM∥AC，
∴∠AEF＝∠MFE，
∴∠AEF＝∠AFE，
∴AE＝AF，
∴AE＝AF＝MF＝ME，
∴四边形AEFM是菱形；
（3）解：解：在△ABC中，
∵∠ACB＝90°，
∴，
∵△AQH∽△ACB，
∴，
即，
∴，
∴．
设菱形AEFM边长为4m，
∵FM∥AC，
∴△BFM∽△BAC，
∴，
即，
∴BM＝3m，BF＝5m，
∴AB＝AF+BF＝4m+5m＝20，
∴，
∴，
∴．
设PQ＝x，
当△HQP∽△MCP时，，
即，
解得；
当△HQP∽△MPC时，，
即，
解得；
经检验，或x＝8或都是原方程的解，
综上所述，满足条件的PQ的值为或8或；
（4）解：解：如图延长线段BC到D，使得DC＝CB＝12，作DM⊥AB于点M，交AC与点G，连接BG，
∴BD＝2BC＝24，∠AMG＝∠ACB＝90°，
∴AC为线段BD的垂直平分线，
∴DG＝BG，
又∵∠A＝∠A，∠AMG＝∠ACB＝90°，
∴△AMG∽△ACB，
∴，
即，
∴，
∴，此时最小，
∵∠DMB＝∠ACB＝90°，∠DBM＝∠ABC，
∴△DMB∽△ACB，
∴，
即，
∴，
∴最小值为．
5．【答案】（1）解：由题意可得：FC∥DE，
则△BFC∽△BED，
故，
即，
解得：BC＝3，
经检验，BC＝3是上述分式方程的解，
∴BC的长为3m；
（2）解：∵AC＝5.4m，
∴AB＝5.4-3＝2.4（m），
∵光在镜面反射中的入射角等于反射角，
∴∠FBC＝∠GBA，
又∵∠FCB＝∠GAB，
∴△BGA∽△BFC，
∴，
∴，
解得：AG＝1.2（m），
∴灯泡到地面的高度AG为1.2m．
6．【答案】（1）解：∵ A(-3，0)．C(1，0)，
∴ AC=4
∵
∴ BC=3
∴ B（1，3）
设过点A、B的直线的函解析式为y=kx+b（k≠0）
∴
解得：k=，b=
∴ 过点A、B的直线的函数解析式是y=x+；
（2）解：由（1）知：AC=4，BC=3，则AB=5
当时，，此时D与C重合，两个三角形全等，则D（1，0）
当时，，则AD=∴ CD=∴ D（，0）
综上，D的坐标为（1，0）或（，0）
（3）解：存在这样的m，m=
由（2）知：D（1，0）或（，0）
①当点D与点C重合时，，则，
∵ AP=DQ=m，∴，解得m=；
②当点D与点C重合时，，则，
∵ AP=DQ=m，∴，解得m=；
③当点D与点C不重合时，，则，
∵ AP=DQ=m，∴，解得m=；
④当点D与点C不重合时，，则，
∵ AP=DQ=m，∴，解得m=；
综上，m的值是
7．【答案】（1）解：由运动知，AP＝4tcm，CQ＝2tcm，
∵AC＝20cm，
∴CP＝（20﹣4t）cm，
∵点P在AC上运动，
∴4t≤20，
∴t≤5，
∵点Q在BC运动，
∴2t≤15，
∴t≤7.5，
∴0≤t≤5，
当t＝3时，CP＝8cm，CQ＝6cm，
在Rt△PCQ中，根据勾股定理得，PQ＝ ＝10（cm）；
（2）解：在Rt△PCQ中，根据勾股定理得，PQ2＝CP2+CQ2，
∵PQ＝4 ，
∴（4 ）2＝（20﹣4t）2+（2t）2，
解得：t＝2或t＝6（舍去），
即当t为2时，PQ的长度等于4
（3）解：∵以点C，P，Q为顶点的三角形与△ABC相似，且∠C＝∠C＝90°，
∴①△CPQ∽△CAB，
∴ ，
∴ ，
∴t＝3，
②△CPQ∽△CBA，
∴ ，
∴ ，
∴t＝ ，
即当t为3或 时，以点C，P，Q为顶点的三角形与△ABC相似．
8．【答案】（1）
（2）解：如图，当点落在上时，
，，
四边形是平行四边形，
，，
，
，
解得，
当点落在边上时，的值为．
（3）解：如图，设直线与边. 交于点，
则，
∽，
，
当直线将的面积分成：的两部分时，有以下两种情况：
的面积：四边形的面积：，
则，
：：，即：：，
解得；
的面积：四边形的面积：，
则，
：：，即：：，
解得，
综上，的值为或．
（4）或
9．【答案】（1）3
（2）
（3）解：方法一：过Q作QM⊥AD，交AD于M，∠QMD＝∠QMA＝90°，
易证四边形ABQM是矩形，∴AM＝BQ＝t，QM＝AB＝3
∴MP＝6－2t，∴PQ2＝PM2＋QM2＝（6－2t）2＋32
∵矩形ABCD，∴∠D＝90°，∴PC2＝PD2＋CD2＝t2＋321分
∵PQ⊥PC，∴∠QPC＝90°，∴PQ2＋PC2＝CQ2
即：（6－2t）2＋32＋t2＋32＝（6－t）2
∴2t2－6t＋9＝0
∵△＝b2－4ac＝36－72＝－36＜0
∴方程无实数根
∴不存在某一时刻t使得PQ⊥PC
方法二：利用相似（△QMP∽△PDC）列方程得2t2－6t＋9＝0，方程无实数根
∴不存在某一时刻t使得PQ⊥PC
（4）解：
∵折叠
，
∵矩形ABCD，∴AD∥BC，
∴∠AQB＝∠PAQ，
∴PA＝PQ＝6－t，
在中，，
∴32＋（6－2t）2＝（6－t）2
即：t2－4t＋3＝0，解得：t1＝1，t2＝3
答：当t等于1或3时，翻折后点B的对应点恰好落在PQ边上。
10．【答案】（1）证明：∵四边形ABCD是矩形，
∴AD∥BC，
.
由轴对称可知∠BFE=∠B'FE，
∴∠DEF=∠GFE，
∴GE=GF；
（2）【方法一】解，如图，过点G作GP⊥BC于点P，则.
点O为矩形ABCD的对称中心.
.
设，则.
在Rt中，.
解得
【方法二】解：如图，延长FG，CD交于点M，
∵四边形ABCD是矩形，
∴AD∥BC，
∴△MGD∽△MFC，
∴，
点O为矩形ABCD的对称中心，.
设，则.
在Rt中，，
（3）证明：①【方法一】证明：如图，过点O作OQ⊥AD于点Q，连结OG，OA，OD
.
点O为矩形ABCD的对称中心，EF过点O，
∴O为EF中点，，
【方法二】解：如图，过点G作GM⊥BC于点M，
则.
，
.
又，
在Rt中，，
，
化简得：ab-4（a+b）+12=0，即（4-a）（4-b）=4.
②如图，连结，
四边形ABFE与关于EF所在直线成轴对称，
，
点O为矩形ABCD的对弥中心，EF过点，
.
同理.
由(1)可知，
，即.
又，
.
又.
.
，即，
.
，
.
.
.
.
，
.
由①可知当时，，可得，
11．【答案】（1）解：四边形是正方形，
，，
是的中点，
，
设，则，
由勾股定理得，
，
，
，舍去，
；
（2）证明：如图，
作于，
四边形是正方形，
，，
，
，
，
，
，
，
，
是的中点，
，
，
≌，
，，
，
，
，，
，
，
，
，
，
，
，
，
，
，
，
，
，
≌，
，，
，
，
，
，
，
；
（3）解：如图，
作，交于，作于，作于，
∽，∽，，
，∽，
，，
，
，
，
当最大时，最大，的面积最大，
，
在以为直径的圆上运动，
当时，，
，
．
12．【答案】（1）解：在正方形中，由折叠得：
在
（2）解：在 上截取 ，使得 ，连接 ，在 上截取 ，使得 ，连接 ，如下图：
在菱形中，
由折叠得：
，
均为等边三角形
在
设
则
解得 ，负值已舍去
13．【答案】（1）
（2）解：如图，将绕点顺时针旋转，得到，连接，
则，
，，
，
，
，
，，，
，
，
，，
≌，
，
，
，
，
，
，
，
解得，
的长是．
（3）解：如图，于，
，
，
，，
∽，
，
，
∽，
，
作的外接圆，在上的下方取一点，连接、，
，
，
，
，
，
当点从点运动到点时，点在上从点运动到点，
点运动的路径的长为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)