第6章 图形的相似精选题（含答案）

中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册苏科版第6章图形的相似精选题
一、选择题
1．已知的面积为16，点D，E分别为AB，AC边上的中点，则四边形DBCE的面积为（　　）
A．12 B．10 C．9 D．8
2．图，电灯在横杆的正上方，在灯光下的影子为，，米，米，点到的距离是2.4米，则到的距离为（　　）
A．3.6米 B．4米 C．5米 D．5.4米
3．如图，△ABC中，E是AB的中点，过点E作ED∥BC，交AC于点D，则△AED与四边形BCDE的面积比是（　　）
A．1：1 B．1：2 C．1：3 D．1：4
4．如图，在平面直角坐标系中，△ABC与△A1B1C1是位似图形.其中BC∶B1C1=1∶2，则△ABC与△A1B1C1的周长之比是（　　）
A．1∶4 B．2∶1 C．1∶2 D．1∶3
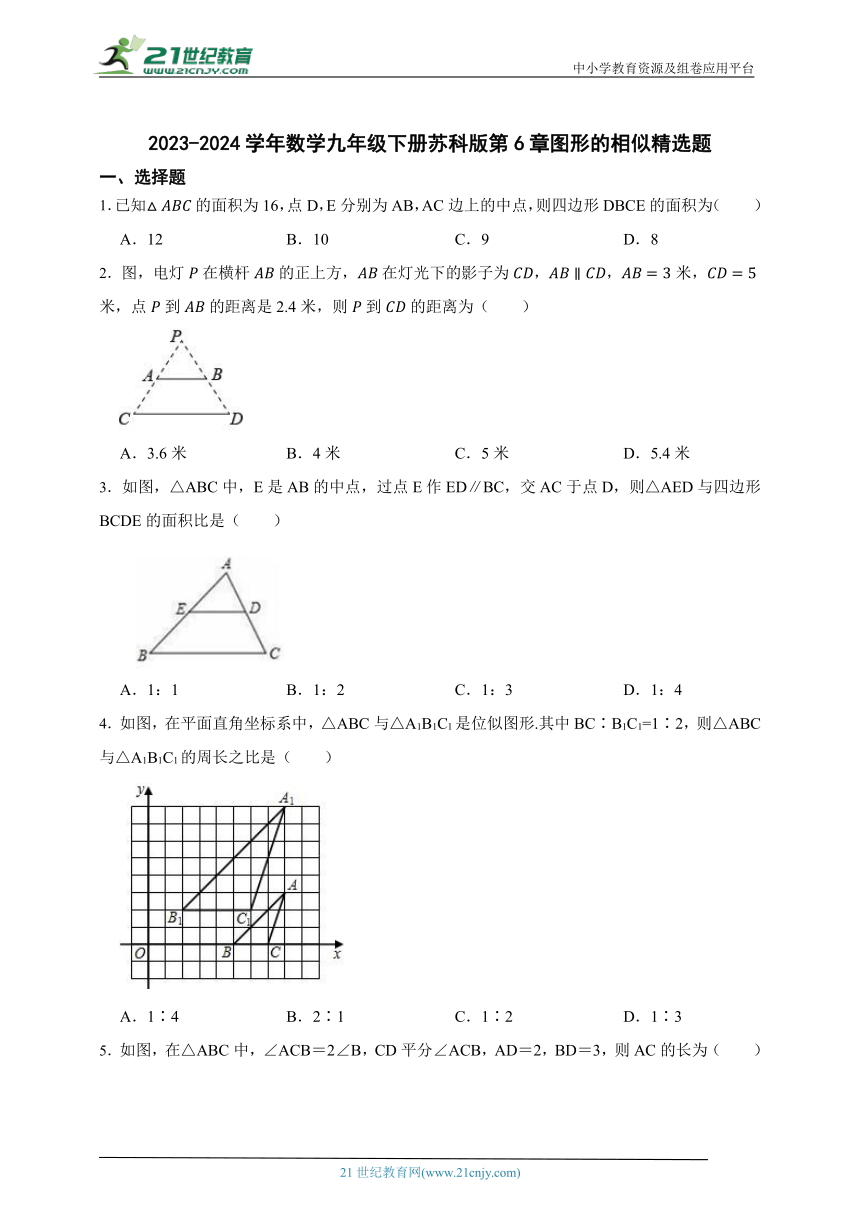
5．如图，在△ABC中，∠ACB＝2∠B，CD平分∠ACB，AD＝2，BD＝3，则AC的长为（　　）
A．3 B． C．4 D．
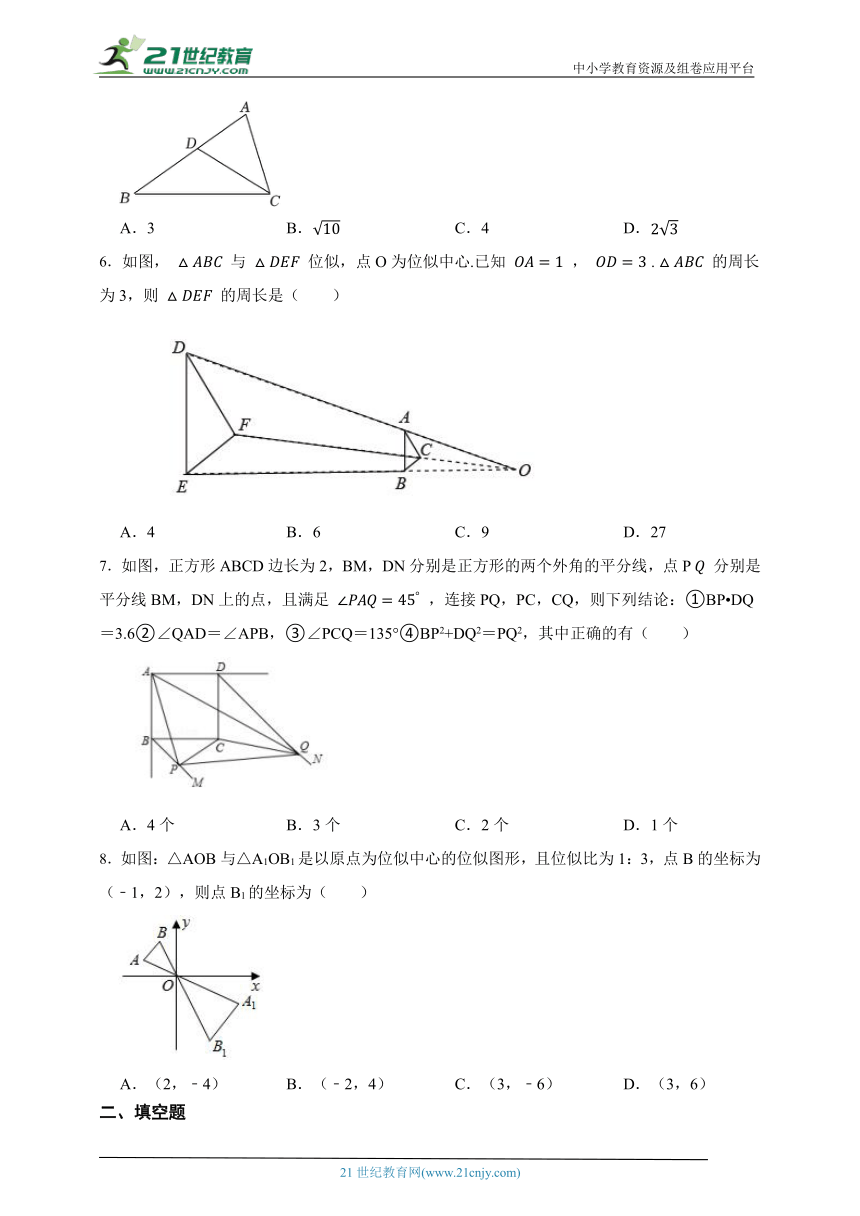
6．如图， 与 位似，点O为位似中心.已知 ， . 的周长为3，则 的周长是（　　）
A．4 B．6 C．9 D．27
7．如图，正方形ABCD边长为2，BM，DN分别是正方形的两个外角的平分线，点P 分别是平分线BM，DN上的点，且满足 ，连接PQ，PC，CQ，则下列结论：①BP DQ＝3.6②∠QAD＝∠APB，③∠PCQ＝135°④BP2+DQ2＝PQ2，其中正确的有（　　）
A．4个 B．3个 C．2个 D．1个
8．如图：△AOB与△A1OB1是以原点为位似中心的位似图形，且位似比为1：3，点B的坐标为（﹣1，2），则点B1的坐标为（　　）
A．（2，﹣4） B．（﹣2，4） C．（3，﹣6） D．（3，6）
二、填空题
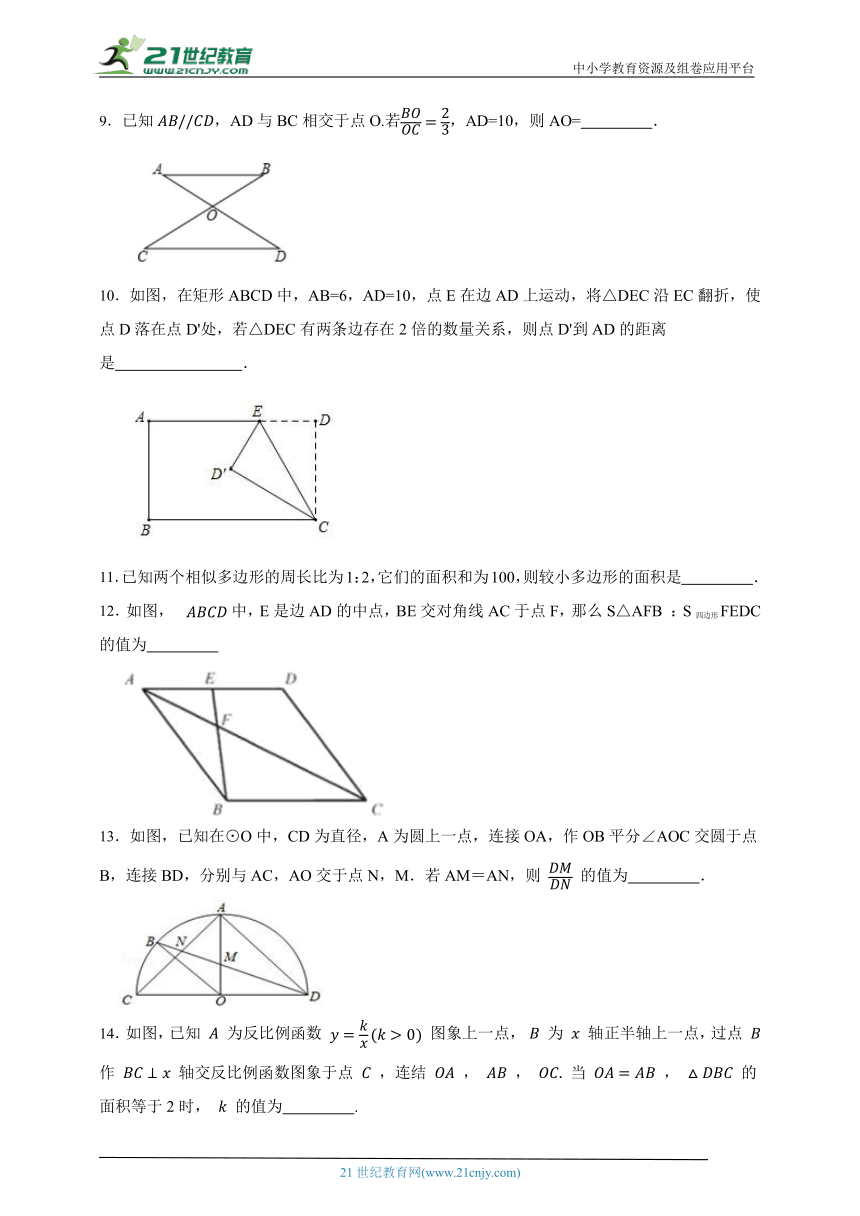
9．已知，AD与BC相交于点O.若，AD=10，则AO=　 　．
10．如图，在矩形ABCD中，AB=6，AD=10，点E在边AD上运动，将△DEC沿EC翻折，使点D落在点D'处，若△DEC有两条边存在2倍的数量关系，则点D'到AD的距离是　 　．
11．已知两个相似多边形的周长比为1：2，它们的面积和为100，则较小多边形的面积是　 　．
12．如图，中，E是边AD的中点，BE交对角线AC于点F，那么S△AFB ：S四边形FEDC的值为　 　
13．如图，已知在⊙O中，CD为直径，A为圆上一点，连接OA，作OB平分∠AOC交圆于点B，连接BD，分别与AC，AO交于点N，M．若AM＝AN，则 的值为　 　．
14．如图，已知 为反比例函数 图象上一点， 为 轴正半轴上一点，过点 作 轴交反比例函数图象于点 ，连结 ， ， 当 ， 的面积等于2时， 的值为　 　.
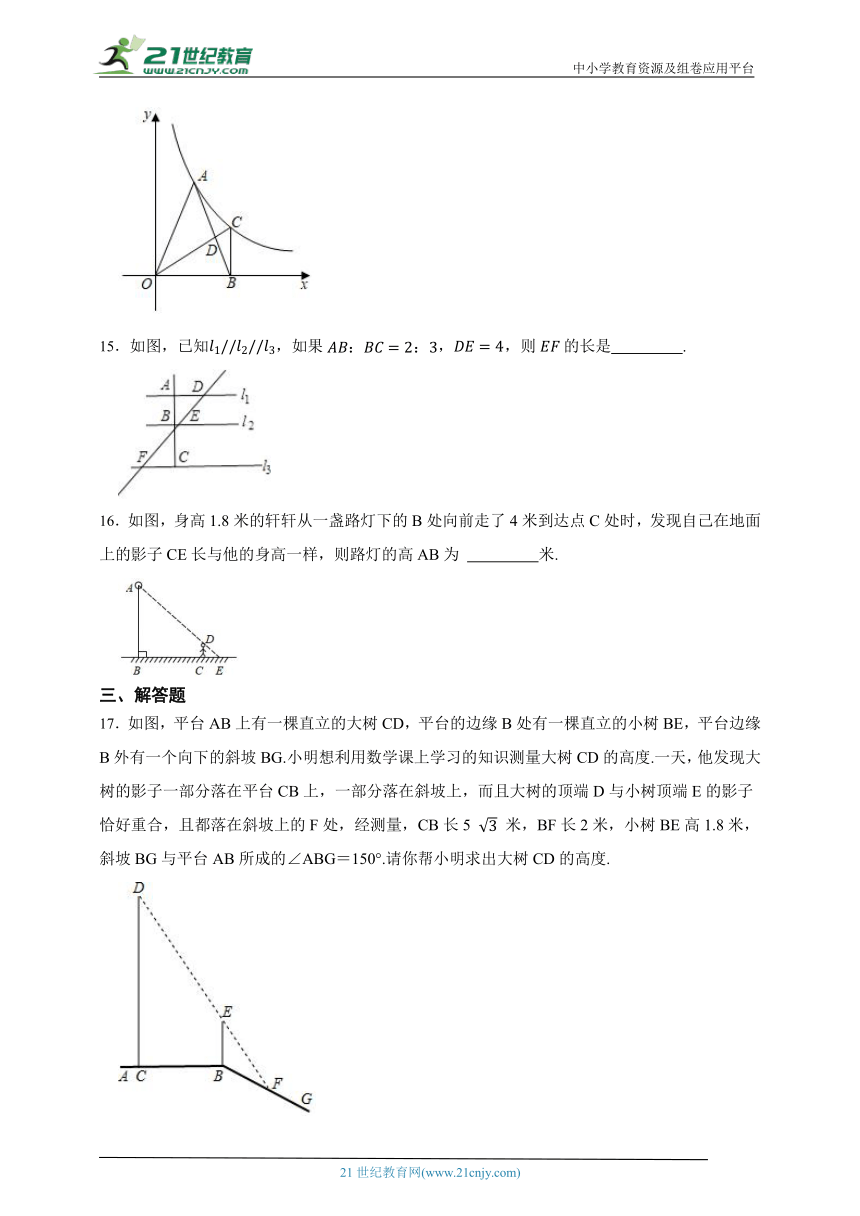
15．如图，已知，如果，，则的长是　 　.
16．如图，身高1.8米的轩轩从一盏路灯下的B处向前走了4米到达点C处时，发现自己在地面上的影子CE长与他的身高一样，则路灯的高AB为 　 　米.
三、解答题
17．如图，平台AB上有一棵直立的大树CD，平台的边缘B处有一棵直立的小树BE，平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天，他发现大树的影子一部分落在平台CB上，一部分落在斜坡上，而且大树的顶端D与小树顶端E的影子恰好重合，且都落在斜坡上的F处，经测量，CB长5 米，BF长2米，小树BE高1.8米，斜坡BG与平台AB所成的∠ABG＝150°.请你帮小明求出大树CD的高度.
18．如图，直线y= 与x轴、y轴分别相交于A，B两点，圆心P的坐标为(1，0)，圆P与y轴相切于点O.若将圆P沿x轴向左移动，当圆P与该直线相交时，求横坐标为整数的点P的个数.
19．如图，在△ABC中，已知AB=AC，D、E、B、C在同一条直线上，且AB2=BD CE，求证：△ABD∽△ECA．
20．如图，AB与CD相交于点O，△OBD∽△OAC， = ，OB=4，求AO和AB的长．
21．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿边AB向点B以2cm/s的速度移动，点Q从B点开始沿边BC以2cm/s的速度移动．如果点P，Q分别从点A，B同时出发，经过几秒钟后，以点P、B、Q三点为顶点的三角形与△ABC相似？
22．如图，在平行四边形中，过点A作，垂足为E，连接，F为线段上一点，且.
（1）求证：；
（2）若，求的长.
答案解析部分
1．【答案】A
2．【答案】B
3．【答案】C
4．【答案】C
5．【答案】B
6．【答案】C
7．【答案】B
8．【答案】C
9．【答案】4
10．【答案】3或或9
11．【答案】20
12．【答案】
13．【答案】
14．【答案】20
15．【答案】6
16．【答案】5.8
17．【答案】解：延长CB交EF于点H，过点F作FM⊥EB的延长线于点M，
∵∠ABG＝150°，BE⊥CB，
∴∠MBF＝150°﹣90°＝60°，
∴∠MFB＝30°，
∵BF的长为2米，
∴BM＝1米，MF＝ 米.
∵BE⊥CB，MF⊥BE，
∴BH∥MF，
∴△EBH∽△EMF，
∴ ＝ .
又∵EB＝1.8米，
∴ ＝ ，
∴BH＝ .
∵BE∥CD，
∴△HBE∽△HCD，
∴ ＝ .
∵CB＝5 ，
∴ ＝ ，
∴CD＝15.8米.
∴大树CD的高度为15.8米.
18．【答案】解：∵直线y= 与x轴、y轴分别相交于A，B两点，∴A点的坐标为(-3，0)，B点的坐标为(0， )，∴AB=2 .如图，将圆P沿x轴向左移动，当圆P与该直线相切于C1时，连结P1C1，则P1C1=1，易知△AP1C1∽△ABO，∴ = ，∴AP1=2，∴P1的坐标为(-1，0)，同理可得P2的坐标为(-5，0).-5与-1之间的整数(不含-5和-1)有：-4，-3，-2，故满足题意的点P的个数是3
19．【答案】证明：
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABD=∠ACE，
∵AB2=BD CE，
∴ = ，即 = ，
∴△ABD∽△ECA
20．【答案】解：
∵△OBD∽△OAC，
∴ = = ，
∴ = ，解得OA=6，
∴AB=OA+OB=4+6=10
21．【答案】解：设经x秒钟△PBQ与△ABC相似，
则AP=2xcm，BQ=2xcm，
∵AB=10cm，BC=20cm，
∴BP=AB﹣AP=（10﹣2x）cm，
∵∠B是公共角．
∵①当 = ，即 = 时，△PBQ∽△ABC，解得x= ；
②当 = ，即 = 时，△QBP∽△ABC，解得x= ．
∴经 或 秒时，以点P、B、Q三点为顶点的三角形与△ABC相似．
22．【答案】（1）证明：∵四边形ABCD是平行四边形
∴，，，
∴，
∵，
∴
∴；
（2）解：∵，
∴
∴
∴
∵四边形ABCD是平行四边形
∴
∵
∴
∴
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)