第7章 锐角函数压轴题特训（含解析）

中小学教育资源及组卷应用平台
2023-2024学年数学九年级下册苏科版第7章锐角函数压轴题特训
1．年月日是我国第个“全国消防宣传日”，该年“消防宣传月”活动的主题是“落实消防责任，防范安全风险”．为落实该主题，济南市消防大队到建东小区进行消防演习．已知，图1是一辆登高云梯消防车的实物图，图2是其工作示意图，起重臂可伸缩（），且起重臂可绕点A在一定范围内转动，张角为（），转动点A距离地面的高度为．
（1）当起重臂长度为，张角，求云梯消防车最高点C距离地面
的高度；
（2）已知该小区层高为，若某居民家突发险情，请问该消防车有效救援能达到几层？请说明理由．（结果精确到，参考数据：，，，）
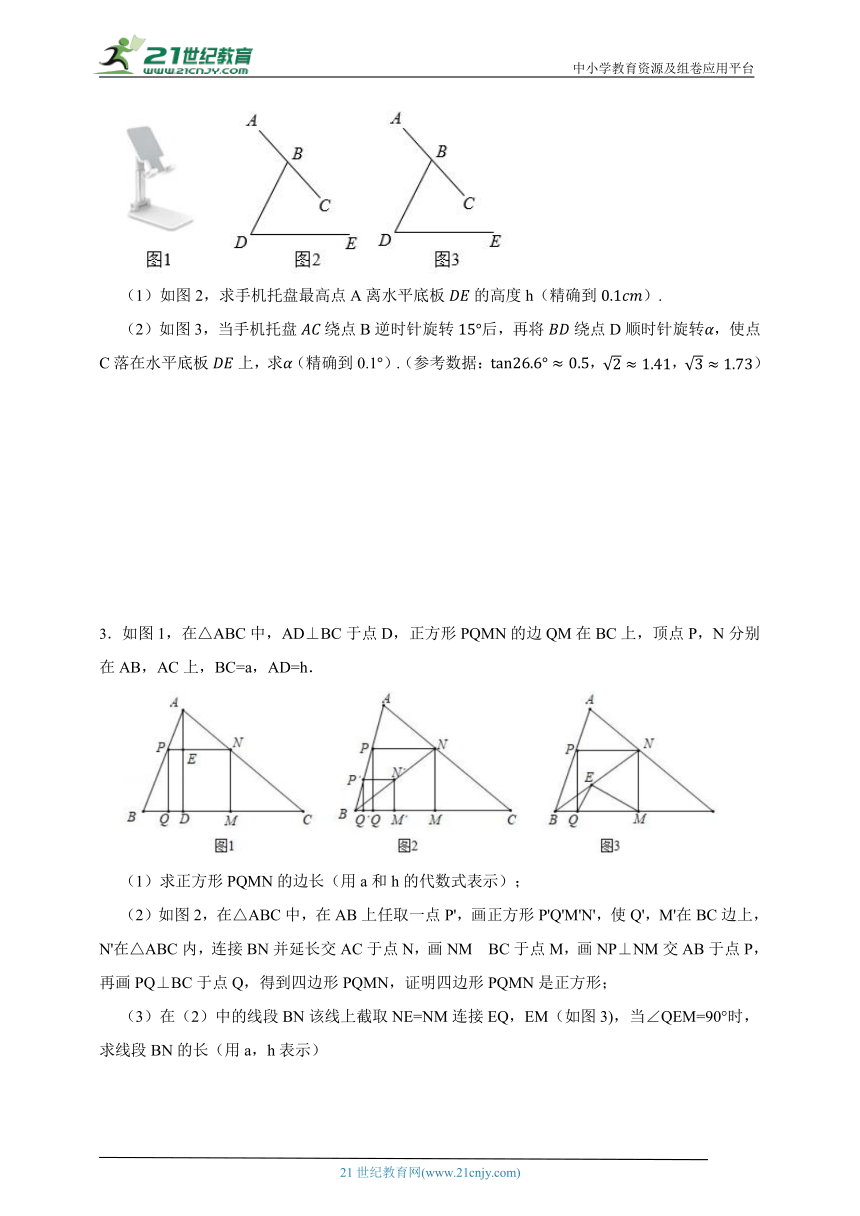
2．如图1是一个简易手机支架，由水平底板、侧支撑杆和手机托盘长组成，侧面示意图如图2所示.已知手机托盘长，侧支撑杆，，，其中点A为手机托盘最高点，支撑点B是的中点，手机托盘可绕点B转动，侧支撑杆可绕点D转动.
（1）如图2，求手机托盘最高点A离水平底板的高度h（精确到）.
（2）如图3，当手机托盘绕点B逆时针旋转后，再将绕点D顺时针旋转，使点C落在水平底板上，求（精确到0.1）.（参考数据：，，）
3．如图1，在△ABC中，AD⊥BC于点D，正方形PQMN的边QM在BC上，顶点P，N分别在AB，AC上，BC=a，AD=h．
（1）求正方形PQMN的边长（用a和h的代数式表示）；
（2）如图2，在△ABC中，在AB上任取一点P'，画正方形P'Q'M'N'，使Q'，M'在BC边上，N'在△ABC内，连接BN并延长交AC于点N，画NM BC于点M，画NP⊥NM交AB于点P，再画PQ⊥BC于点Q，得到四边形PQMN，证明四边形PQMN是正方形；
（3）在（2）中的线段BN该线上截取NE=NM连接EQ，EM（如图3)，当∠QEM=90°时，求线段BN的长（用a，h表示）
4． 如图，是的直径，点是圆上的一点，于点，交于点，连接，若平分，过点作于点交于点．
（1）求证：是的切线；
（2）延长和交于点，若，求的值；
（3）在的条件下，求的值．
5．如图，在中，，，，动点、分别在边、上，且，设过点作，与直线相交于点．
（1）当时，求的值；
（2）当时，求的值；
（3）当与相似时，求的长．
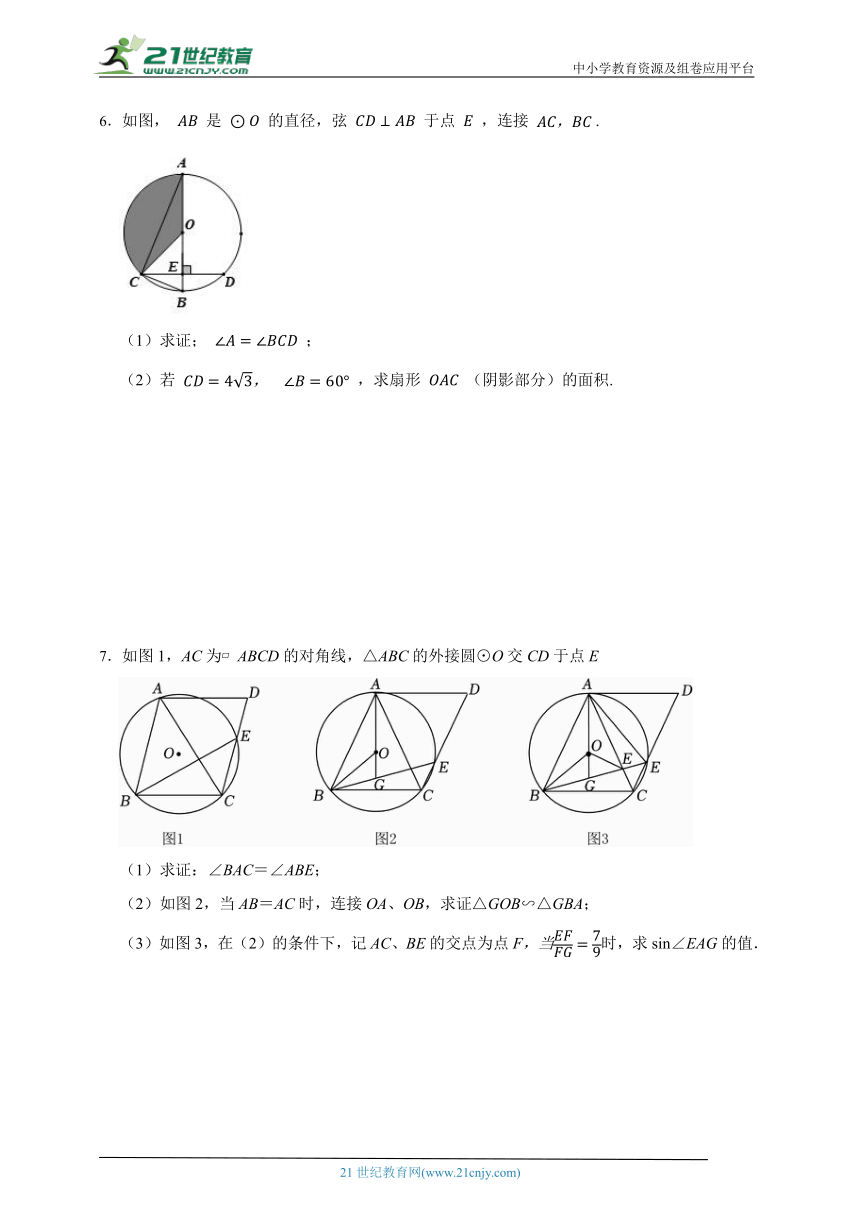
6．如图， 是 的直径，弦 于点 ，连接 .
（1）求证； ；
（2）若 ，求扇形 （阴影部分）的面积.
7．如图1，AC为 ABCD的对角线，△ABC的外接圆⊙O交CD于点E
（1）求证：∠BAC＝∠ABE；
（2）如图2，当AB＝AC时，连接OA、OB，求证△GOB∽△GBA；
（3）如图3，在（2）的条件下，记AC、BE的交点为点F，当时，求sin∠EAG的值．
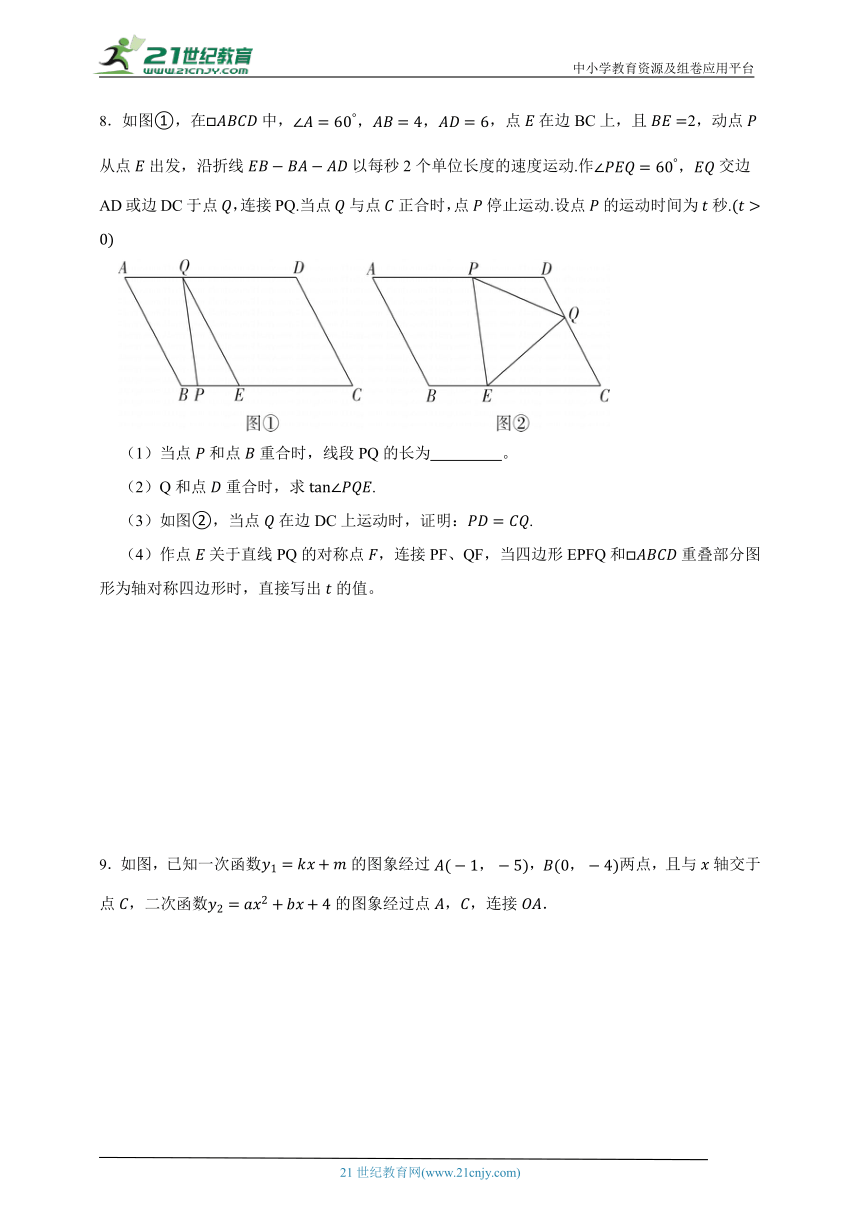
8．如图①，在中，，点在边BC上，且2，动点从点出发，沿折线以每秒2个单位长度的速度运动.作交边AD或边DC于点，连接PQ.当点与点正合时，点停止运动.设点的运动时间为秒.
（1）当点和点重合时，线段PQ的长为　 　。
（2）Q和点重合时，求.
（3）如图②，当点在边DC上运动时，证明：.
（4）作点关于直线PQ的对称点，连接PF、QF，当四边形EPFQ和重叠部分图形为轴对称四边形时，直接写出的值。
9．如图，已知一次函数的图象经过，两点，且与轴交于点，二次函数的图象经过点，，连接．
（1）求一次函数和二次函数的解析式．
（2）求的正弦值．
（3）在点右侧的轴上是否存在一点，使得与相似？若存在，求出点的坐标；若不存在，请说明理由．
10．在平面直角坐标系中，点O为坐标原点，直线交x轴于点B，交y轴于点A，．
（1）如图1，求k的值；
（2）如图2，点H在AB上，点F在OB上，连接FH、OH，且，过点F作AB的垂线，垂足为点S，设点H的横坐标为t，，线段SH的长为d，求d与t之间的函数关系式；
（3）如图3，在（2）的条件下，将线段OH绕点O顺时针旋转得到线段OE，连接AE并延长交x轴于C，连接HC，点K是HC的中点，连接EK，当时，求的面积．
11．如图，抛物线经过点，与轴交于点，点为第一象限内抛物线上一动点．
（1）求抛物线的解析式．
（2）直线与轴交于点，与轴交于点，过点作直线轴，交于点，连接，当时，求点的横坐标．
（3）如图，点为轴正半轴上一点，与交于点，若，，求点的坐标．
12．如图，山区某教学楼后面紧邻着一个土坡，坡面BC平行于地面AD，斜坡AB的坡比为i=1：，且AB=26米．
（1）求坡顶与地面的距离BE的长．
（2）为了防止山体滑坡，保障安全，学校决定对该土坡进行改造．经地质人员勘测，当坡角不超过53°时，可确保山体不滑坡．学校计划将斜坡AB改造成AF(如图所示)，那么BF至少是多少米？(结果精确到1米)(参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.33)．
13．图1是某越野车的侧面示意图，折线段表示车后盖，已知，，，该车的高度．如图2，打开后备箱，车后盖落在处，与水平面的夹角．
（1）求打开后备箱后，车后盖最高点到地面的距离；
（2）若小琳爸爸的身高为，他从打开的车后盖处经过，有没有碰头的危险 请说明理由．
（结果精确到，参考数据：，，，）
14．如图，是的直径，点是圆上的一点，于点，交于点，连接，若平分，过点作于点，交于点，延长，交于点．
（1）求证：是的切线；
（2）求证：；
（3）若，求的值．
答案解析部分
1．【答案】（1）解：如图所示，过点C作，垂足为F，过点A作，垂足为G，
则，，
∵，
∴，
在中，，，
∴（），
∴（），
∴云梯消防车最高点C距离地面的高度为．
（2）解：该消防车能有效救援层，理由如下，
当，时，能达到最高高度，
∵，
∴，
在中，，
∴（），
∴（），
∵，
∴该消防车能有效救援层．
2．【答案】（1）解：如图2，作于点F，，于点G，
∵，
∴，
又∵，
∴，
∵，
∴，
∴，
∵，B是的中点，
∴
∴，
∴；
（2）解：由条件，得：，
又∵，，
∴，
∴，
∴.
3．【答案】（1）解：如图1，
在正方形PQMN中，
，
，
，
，
，
；
（2）证明：如图2，
，
∴四边形PQMN是矩形，
，
，
矩形PQMN是正方形；
（3）解：如图3
作NR⊥EM于，作于，
∴∠QEM=∠NRM=90°，
∴∠EQM+∠TME=90°，
∵∠NMT=90°，
∴∠TME+∠RMN=90°，
∴∠EQM=∠NMR，
∵MN=MQ，
∴△QEM≌△MRN(AAS)，
∴EQ=RM，
∵EN=NM，
∴EM=2RM，
∴EM=2EQ，
∴tan∠EQM=2，
∴sin∠EQM=，
∴EM=QM·sin∠EQM=，
∴ET=EM·sin∠EMQ=，
4．【答案】（1）证明：如图，连接，
，
，
平分，
，
，
，
，
，
是的半径，
是的切线；
（2）解：，，
设，则，
，
，
，
；
（3）解：由知：，，
，
，
，
，
，，
，
，
∽，
．
5．【答案】（1）解：过作，垂足为点，
，
．
，
，
，
又，，
，；
（2）解：当时，得，，．
，
点是射线与直线的交点，
过作，交于点，
则．
，．
，
，，
，
（3）解：a.当点是射线与的交点时，
与相似，
又，
，即，
又，
∽．
，
即．
解得，
过作，垂足为点．
由，得，，．
，
．
．
，
．
解得，
，
b.当点是射线与的交点时，
，，
又与相似，
．
，，
∽，
即解得．
，
，
．
．
解得．
综上所述，当与相似时，的长为或．
6．【答案】（1）解：证明； 是 的直径，弦 ，
，
（2）解： ，
为等边三角形，
，
，
是 的直径，弦 ， ，
，
在 中， ，
∴扇形 （阴影部分）的面积 .
7．【答案】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ABE＝∠BEC，
∵弧BC＝弧BC，
∴∠BAC＝∠BEC，
∴∠BAC＝∠ABE；
（2）证明：∵AB＝AC，AO经过圆心，
∴∠BAG＝∠CAG，
∵OA＝OB，
∴∠OAB＝∠OBA，
∵∠BAC＝∠ABE，
∴∠OAB＝∠OBA＝∠OBG，
又∠BGO＝∠AGB，
∴△GOB∽△GBA；
（3）解：延长AO交BC于点H，连接CG，
则AH⊥BC，BH=CH，
∴∠GBH=∠GCH，
∵∠ABC=∠ACB，
∴∠GCF=∠ABE=∠BEC，
∵∠CGF=∠EGC，
∴△CGF≌△EGC，
∴，
∴CG=，
∵∠ABE＝∠ACE＝∠BEC，
∴EF＝FC，
∵，
设EF＝CF＝7a，
则FG＝9a，GE＝16a，
∴BG＝CG＝＝12a，
∵，
∴，
∵∠GCF＝∠ECF，即CF是∠ECG的平分线，
∴点F到∠ECG两边的距离相等，
∴，
∴，
∵AB∥CD，
∴△CEF∽△ABF，
∴，
即，
∴AB＝28a，
由（2）可知：OB是∠ABG的平分线，同理，
即，
∴，
设⊙O的半径为R，
∵BG2＝GO GA，
∴（12a）2＝，
解得：，
即，
设OH＝x，
在Rt△ABH和Rt△OBH中，（28a）2-（R+x）2＝R2-x2，
整理得：，
即，
∵∠CAE＝∠CBE，∠CAG＝∠OBG，
∴∠EAG＝∠OBH，
∴．
8．【答案】（1）
（2）解：当点Q与点D重合时：
∵四边形ABCD是平行四边形，
∴CD=AB=4，∠C=∠A=60°，BC=AD=6，
又∵BE=2，
∴CE=BC-BE=6-2=4，
∴CD=CE，
∴△CDE是等边三角形，
∴∠CEQ=60°，
∵AD∥BC，
∴∠PQE=∠CEQ=60°，
∴ =
（3）证明：连接ED，
由（2）知：△CED是等边三角形，
∴∠CED=60°，ED=EC，
∵∠PEQ=60°，
∴∠CED=∠PEQ，
∴∠PEQ-∠DEQ=∠CED-∠DEQ，
即∠DEP=∠CEQ，
∵AD∥BC，
∴∠EDP=∠CED=60°，
∴∠EDP=∠C，
∴△PED≌△QEC（ASA），
∴PD=QC；
（4）解：可根据点P的运动过程进行分类讨论：
①当点P在BE上时， 四边形EPFQ和重叠部分图形不可能为轴对称四边形 ；
②当点P在AB上时，如图所示，点F与点A重合，过点P作PT⊥BC，垂足为点T，
∵AD∥BC，∠A=60°，
∴∠ABT=∠A=60°，
∴∠BPT=30°，
设BP=x，则：BT=，PT=，
∴ET=2+，
∴AP=AB-BP=4-x，
∴EP=AP=4-x，
在Rt△PET中，根据勾股定理，可得：（4-x）2=（）2+（2+）2，
解得：x=，
∴（秒）；
③当点P在AD上，点Q也在AD上时，点Q与点D重合，如图所示，
由（2）知。△CDE是等边三角形，
∴∠DEC=60°，
∵AD∥BC，
∴∠PDE=∠DEC=60°，
∵∠PEQ=60°，
∴△PDE也是等边三角形，
∴PD=DE=CD=4，
∴AP=6-4=2，
∴t=（秒）
④当点P在AD上，点Q在CD上时，则点D在EF上，如图所示，
由（3）知PD=CQ，
又由轴对称图形的性质知：PD=DQ，
∴PD=CQ=DQ=2，
∴AP=AD-PD=6-2=4，
∴t=（秒）；
综上所述，可得出 当四边形EPFQ和重叠部分图形为轴对称四边形时， t的值为：或4或5。
9．【答案】（1）解：将，代入，
，
解得，
，
令，则，
，
将，代入，
，
解得，
；
（2）解：过点作交于，
，，
，
，
，
，
，
，
；
（3）解：存在点，使得与相似，理由如下：
点在点右侧，
，
，
或，
当时，∽，
，
，，，
，
；
当时，∽，
，
，
；
综上所述：点坐标为或．
10．【答案】（1）解：∵ 直线y=kx+6k交x轴于点B，
∴取y＝0，得x＝6，∴B点的坐标为（-6，0）.
在Rt△AOB中，∵∠AOB=90°，AB=2AO，
∴设OA=x，则AB＝2x，
∴，解得(负值舍去).
∴A点的坐标为（0，）
∵A点在直线y=kx+6k的图象上，
∴6k=，解得；
（2）解：过点H作轴，轴 ，
∵，
∴直线AB的表达式.
设点H的坐标为，
∵HO=HF，
∴FK=OK=HG=-t，
∴BF=6-OF=6+2t，
∴，
∴
∴ 线段SH的长为
= （-3＜t＜-1） .
（3）解：如图，连结OK并延长，交AC于点L，
∵线段OH绕点O顺时针旋转60°得到线段OE，
∴OH=OE，∠HOE=60°，
∴△HEO为等边三角形，
∴∠HAO=∠HEO=60°，
∴点A、H、O、E四点共圆，
∴∠OAC=60°，
∴OA平分∠BAC，
又BC⊥OA，
∴AO是BC边的中线，
∴BO＝OC．
∵点K是HC的中点，
∴OK//BH.
∴KL//AH，K是HC的中点，
∴L是AC的中点.
∴△AOL是等边三角形，
∴OL=AO.
∵∠HOA+∠AOE=∠AOE+∠EOL=60°，
∴∠HOA=∠EOL，
∵OH=OE，
∴△AHO≌△LEO（SAS），
∴EL=AH=2KL，
∵∠OLA=60°，
过点E作EK′⊥LO，则，
∴点E′、E重合，
∴EK⊥LK，
∵∠AGH=∠EKL=90°，AH=EL，∠ELK=∠HAG=60°
△AHG≌△EKL（AAS），
∴EK=HG=-t，
∴
当时，，
解得：t1=1（舍）t2=-2，
∴
11．【答案】（1）解：把（3，1）和（0，5）代入到解析式中可得：，
解得，
抛物线的解析式为：；
（2）解：直线中，令可得，
直线中，令，可得，
分别过E、F向y轴作垂线，垂足为G、H，根据题意可得EG=FH，
轴，轴，
和为直角三角形，
在和中：
，
≌，
，
设，则，
，，
从而，，
则有，解得舍去或，
故E点的横坐标为：；
（3）解：将OE平移到NP，连接EP，则四边形ONPE为平行四边形，，
过P作PQ⊥BN于Q，过Q作QR⊥y轴于R，过P作PS⊥RQ交延长线于S，延长PE交y轴于T，
设，则，，，
轴，
∽，
，
，
∴，，
设，
，，，
，
，
，
，
∽，
，
，，则，
，
，
，代入抛物线解析式中有：
，
解得：或，
当时，；
当时，
12．【答案】（1）解：设AE=5x米，
∵斜坡AB的坡比为，
∴BE=12x米，
由勾股定理得，AE2+BE2=AB2，即(5x)2+(12x)2=262，
解得，x=2或x=-2(舍去) ，
∴BE=12x=24(米)；
（2）解：如图：过点F作FG⊥AD于G，
则四边形FGEB为矩形，
∴FG=BE=24米，BF=GE，
在Rt△AFG中，∠FAG=53°，
∴(米)，
由(1)可知，AE=10米，
∴BF=GE=AG-AE≈8(米)，
答：BF至少是8米．
13．【答案】（1）解：如图，作，垂足为点
在中
∵，
∴
∴
∵平行线间的距离处处相等
∴
答：车后盖最高点到地面的距离为．
（2）解：没有危险，理由如下：
过作，垂足为点
∵，
∴
∵
∴
在中，
∴．
∵平行线间的距离处处相等
∴到地面的距离为．
∵
∴没有危险．
14．【答案】（1）连接
∵平分，
∴，
∵，
∴，
∴，
∴，
∵，
∴，
∴是的切线．
（2）证明，如下：
由（1）得，，
∵，
∵，
∴，
∴，
∵，
∴，
∴，
∴．
（3）∵，
∴，
设的半径为，
∴，
∴，
∵，
∴，，
∵，
∴，
∵，
∴，
∵，
∴．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)