第7章 数据的收集、整理、描述督单元测试(含答案)
文档属性
| 名称 | 第7章 数据的收集、整理、描述督单元测试(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 626.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2023-2024学年数学八年级下册苏科版第7章数据的收集、整理、描述
一、选择题
1.了解时事新闻,关心国家重大事件是每个中学生应具备的素养,在学校举行的新闻事件比赛中,知道“祝融号”成功到达火星的同学有40人,频率为0.8,则参加比赛的同学共有( )
A.32人 B.40人 C.48人 D.50人
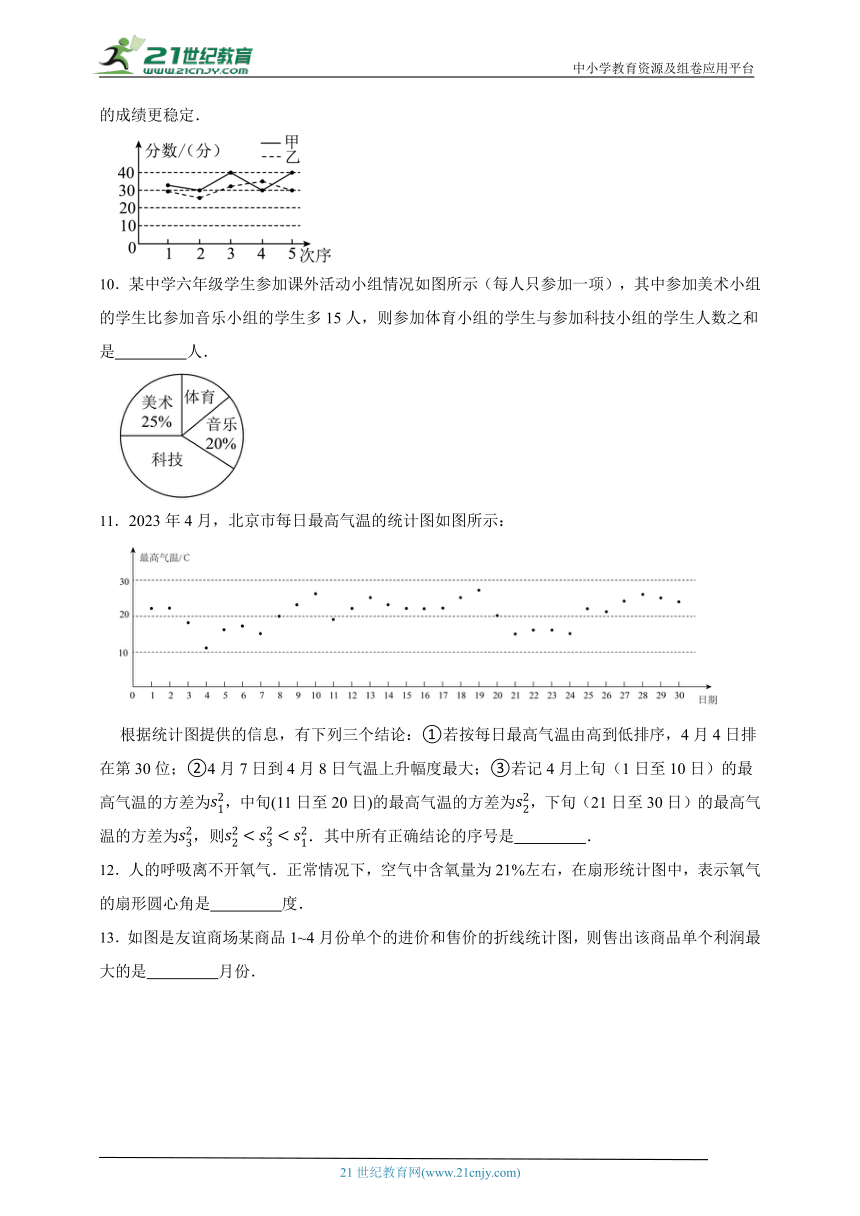
2.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5 分),则所打分数的众数为( )
课后延时服务的打分情况扇形统计图
A.5分 B.4分 C.3分 D.45%
3.如图是某学校全体教职工年龄的频数分布直方图(每组年龄包含最小值,不包含最大值),根据图形提供的信息,下列说法中错误的是( )
A.该学校教职工总人数是50人
B.这一组年龄在小组的教职工人数占该学校全体教职工总人数的
C.教职工年龄的中位数一定落在这一组
D.教职工年龄的众数一定在这一组
4.为了解某市万名学生平均每天读书的时间,请你运用数学的统计知识将统计的主要步骤进行排序:
①得出结论,提出建议;
②分析数据;
③从万名学生中随机抽取名学生,调查他们平均每天读书的时间;
④利用统计图表将收集的数据整理和表示.
合理的排序是( )
A.③②④① B.③④②① C.③④①② D.②③④①
5.有下列事件:(1)调查长江现有鱼的数量;(2)调查你班每位同学穿鞋的尺码;(3)了解一批电视机的使用寿命;(4)校正某本书上的印刷错误.其中最适合普查的是( )
A.(1)(3) B.(1)(4) C.(2)(3) D.(2)(4)
6.下表是某篮球队的年龄分布,对于不同的值,下列关于年龄的数据量不会发生改变的是( )
年龄岁
频数
A.平均数、中位数 B.中位数、众数
C.中位数、方差 D.平均数、方差
7.统计的一般过程可以用下面框图所示的步骤进行,其中表示的是( )
A.确定调查范围 B.设计调查选项
C.整理数据 D.选择调查方式
8.下列说法正确的是( )
A.九年级某班的英语测试平均成绩是98.5分,说明每个同学的得分都是98.5分
B.数据4,4,5,5,0的中位数和众数都是5
C.要了解一批日光灯的使用寿命,应采用全面调查
D.若甲、乙两组数据中各有20个数据,两组数据的平均数相等,方差=1.25,=0.96,则说明乙组数数据比甲组数据稳定
二、填空题
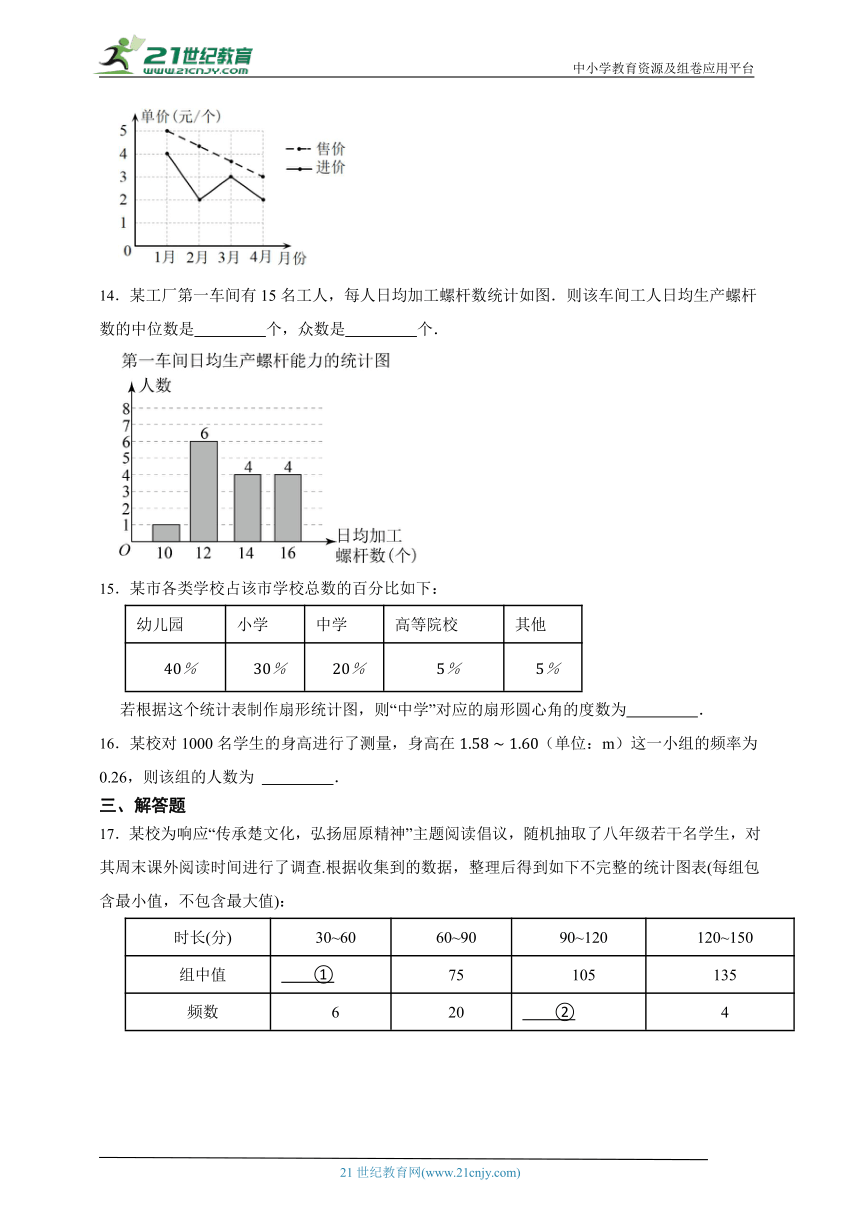
9.如图是甲乙两位同学在参加体育中考前的次体能测试成绩折线统计图,由图可知, 的成绩更稳定.
10.某中学六年级学生参加课外活动小组情况如图所示(每人只参加一项),其中参加美术小组的学生比参加音乐小组的学生多15人,则参加体育小组的学生与参加科技小组的学生人数之和是 人.
11.2023年4月,北京市每日最高气温的统计图如图所示:
根据统计图提供的信息,有下列三个结论:①若按每日最高气温由高到低排序,4月4日排在第30位;②4月7日到4月8日气温上升幅度最大;③若记4月上旬(1日至10日)的最高气温的方差为,中旬(11日至20日)的最高气温的方差为,下旬(21日至30日)的最高气温的方差为,则.其中所有正确结论的序号是 .
12.人的呼吸离不开氧气.正常情况下,空气中含氧量为21%左右,在扇形统计图中,表示氧气的扇形圆心角是 度.
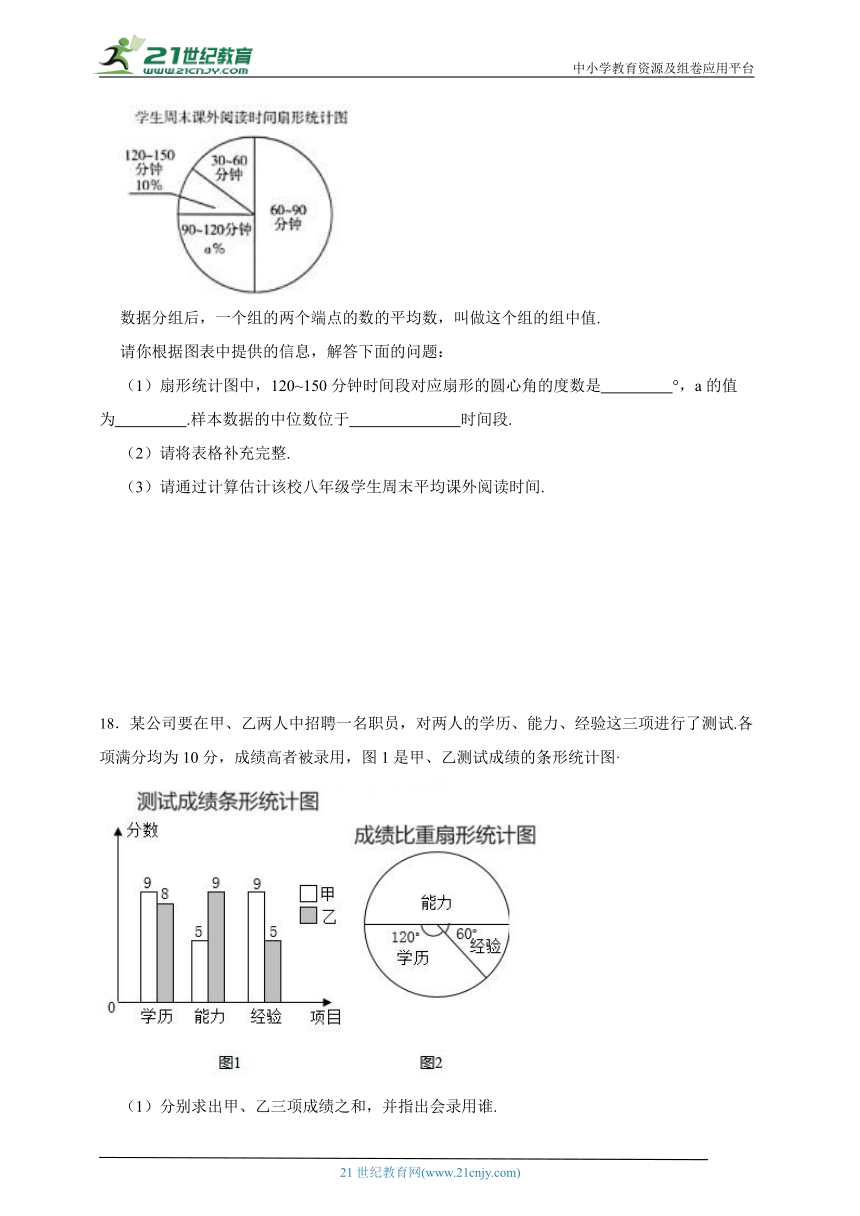
13.如图是友谊商场某商品1~4月份单个的进价和售价的折线统计图,则售出该商品单个利润最大的是 月份.
14.某工厂第一车间有15名工人,每人日均加工螺杆数统计如图.则该车间工人日均生产螺杆数的中位数是 个,众数是 个.
15.某市各类学校占该市学校总数的百分比如下:
幼儿园 小学 中学 高等院校 其他
若根据这个统计表制作扇形统计图,则“中学”对应的扇形圆心角的度数为 .
16.某校对1000名学生的身高进行了测量,身高在(单位:m)这一小组的频率为0.26,则该组的人数为 .
三、解答题
17.某校为响应“传承楚文化,弘扬屈原精神”主题阅读倡议,随机抽取了八年级若干名学生,对其周末课外阅读时间进行了调查.根据收集到的数据,整理后得到如下不完整的统计图表(每组包含最小值,不包含最大值):
时长(分) 30~60 60~90 90~120 120~150
组中值 ① 75 105 135
频数 6 20 ② 4
数据分组后,一个组的两个端点的数的平均数,叫做这个组的组中值.
请你根据图表中提供的信息,解答下面的问题:
(1)扇形统计图中,120~150分钟时间段对应扇形的圆心角的度数是 °,a的值为 .样本数据的中位数位于 时间段.
(2)请将表格补充完整.
(3)请通过计算估计该校八年级学生周末平均课外阅读时间.
18.某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试.各项满分均为10分,成绩高者被录用,图1是甲、乙测试成绩的条形统计图·
(1)分别求出甲、乙三项成绩之和,并指出会录用谁.
(2)将甲、乙的三项测试成绩按照扇形统计图(如图2)各项所占之比,分别计算各自的综合成绩,并判断是否会改变(1)的录用结果
19.某中学为加强学生的劳动教育,需要制定学生每周劳动时间(单位:时)的合格标准,为此随机调查了 100 名学生目前每周劳动时间,获得数据并整理成下表.
每周劳动时间x(时) 0.5≤x<1.5 1.5≤x<2.5 2.5≤x<3.5 3.5≤x<4.5 4.5≤x<5.5
组中值 1 2 3 4 5
人数 21 30 19 18 12
(1)画扇形图描述数据时,1.5≤x<2.5这组数据对应的扇形的圆心角是多少度
(2)估计该校学生目前每周劳动时间的平均数.
(3)请你为该校制定一个学生每周劳动时间的合格标准(时间取整数小时),并用统计量说明其合理性.
20.某中学开展“迎接党的二十大”知识比赛,九年级(1)班、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写表格:
班级 中位数 平均数 众数
九(1)班 85 ? 85
九(2)班 ? 85 ?
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?说明理由;
(3)如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由.
21.某教育局为了解初中毕业年级学生的体质情况,从某校九年级学生中随机抽取20%的学生进行体质监测.根据《中学生体质健康标准》规定学生体质健康等级标准:90分及以上为优秀;80分~89分为良好;60分~79分为及格;60分以下为不及格,将测试成绩制成如下图表.
各等级学生频率分布表
成绩 频数 频率
优秀 16 b
良好 a 0.24
及格 18 0.36
不及格 4 0.08
请根据图表信息回答下列问题:
(1)表格中的a=_ ,b=_ .
(2)已知“80分~89分”这组的数据如下:81,83,84,85,85,81,80,86,87,88,83,85,则所抽取的这些学生体质监测成绩的中位数是 _ .
(3)求参加本次体质监测的学生的平均成绩.
(4)请估计该校九年级体质监测成绩未达到“良好”等级及以上的学生人数.
22.某校对八年级的名学生进行了一次体育测试测试完成后,在甲、乙两班各抽取了名学生的测试成绩,对数据进行整理分析,并给出了下列信息:
甲班名同学的测试成绩统计如下:,,,,,,,,,,,,,,,,,,,.
乙班名同学的测试成绩统计如下:
组别
频数
其中,乙班名同学的测试成绩高于,但不超过分的成绩如下:,,,,,.
甲、乙两班抽取的学生的测试成绩的平均数、中位数、众数如表所示:
班级 平均数 中位数 众数
甲班
乙班
(1)根据以上信息可以写出: , , ;
(2)你认为甲、乙两个班哪个班的学生体育测试成绩较好,请说明理由;
(3)若规定分及以上为优秀,请估计该校八年级参加此次测试的学生中优秀的学生有多少人.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】乙
10.【答案】
11.【答案】①③
12.【答案】75.6
13.【答案】2
14.【答案】14;12
15.【答案】72°
16.【答案】260人
17.【答案】(1)36;25;60~90分钟
(2)①:45,②:10
(3)84分钟
18.【答案】(1)解:由题意得,甲三项成绩之和为:9+5+9=23(分),
乙三项成绩之和为:8+9+5=22(分),
∵23>22,
∴会录用甲;
(2)解:由题意得,甲三项成绩之加权平均数为:(分),
乙三项成绩之加权平均数为:(分),
∵7<8,
∴会改变(1)的录用结果.
19.【答案】(1)解:∵×100%=30%,
∴ 1.5≤x<2.5这组数据对应的扇形的圆心角=360°×30%=108°;
(2)解:=2.7(小时);
(3)解:从平均数看,标准可以定为3小时,理由:平均数为2.7小时,则可知该校学生目前每周劳动时间平均值为27小时,把标准定为3小时,至少有30%的学生每周劳动时间可达标,同时还有至少还有51%的学生未达标,这样使大多数学生有更高的努力的目标.
20.【答案】(1)85、80、100
(2)解:九(1)的复赛成绩较好;
理由:因为两个班的平均数相同,九(1)班的中位数高,所以九(1)班的复赛成绩较好;
(3)解:九(1)班成绩稳定些,能胜出;
理由:,
,
因为,
所以九(1)班成绩稳定些,能胜出.
21.【答案】(1)12;0.32
(2)82
(3)解:=(92×16+84×12+70×18+45×4)÷50=78.4.
答:参加本次体质监测的学生的平均成绩为 78.4.
(4)(4+18)÷20%=110(人).
答:该校九年级体质监测成绩未达到“良好”等级及以上的学生人数约为 110 人
22.【答案】(1)3;48;50
(2)解:甲班的成绩好.
理由:甲乙两班的平均数相等,甲班的中位数和众数都比乙班的大;
(3)解:(人),
答:估计该校八年级参加此次测试的学生中优秀的学生有人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年数学八年级下册苏科版第7章数据的收集、整理、描述
一、选择题
1.了解时事新闻,关心国家重大事件是每个中学生应具备的素养,在学校举行的新闻事件比赛中,知道“祝融号”成功到达火星的同学有40人,频率为0.8,则参加比赛的同学共有( )
A.32人 B.40人 C.48人 D.50人
2.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5 分),则所打分数的众数为( )
课后延时服务的打分情况扇形统计图
A.5分 B.4分 C.3分 D.45%
3.如图是某学校全体教职工年龄的频数分布直方图(每组年龄包含最小值,不包含最大值),根据图形提供的信息,下列说法中错误的是( )
A.该学校教职工总人数是50人
B.这一组年龄在小组的教职工人数占该学校全体教职工总人数的
C.教职工年龄的中位数一定落在这一组
D.教职工年龄的众数一定在这一组
4.为了解某市万名学生平均每天读书的时间,请你运用数学的统计知识将统计的主要步骤进行排序:
①得出结论,提出建议;
②分析数据;
③从万名学生中随机抽取名学生,调查他们平均每天读书的时间;
④利用统计图表将收集的数据整理和表示.
合理的排序是( )
A.③②④① B.③④②① C.③④①② D.②③④①
5.有下列事件:(1)调查长江现有鱼的数量;(2)调查你班每位同学穿鞋的尺码;(3)了解一批电视机的使用寿命;(4)校正某本书上的印刷错误.其中最适合普查的是( )
A.(1)(3) B.(1)(4) C.(2)(3) D.(2)(4)
6.下表是某篮球队的年龄分布,对于不同的值,下列关于年龄的数据量不会发生改变的是( )
年龄岁
频数
A.平均数、中位数 B.中位数、众数
C.中位数、方差 D.平均数、方差
7.统计的一般过程可以用下面框图所示的步骤进行,其中表示的是( )
A.确定调查范围 B.设计调查选项
C.整理数据 D.选择调查方式
8.下列说法正确的是( )
A.九年级某班的英语测试平均成绩是98.5分,说明每个同学的得分都是98.5分
B.数据4,4,5,5,0的中位数和众数都是5
C.要了解一批日光灯的使用寿命,应采用全面调查
D.若甲、乙两组数据中各有20个数据,两组数据的平均数相等,方差=1.25,=0.96,则说明乙组数数据比甲组数据稳定
二、填空题
9.如图是甲乙两位同学在参加体育中考前的次体能测试成绩折线统计图,由图可知, 的成绩更稳定.
10.某中学六年级学生参加课外活动小组情况如图所示(每人只参加一项),其中参加美术小组的学生比参加音乐小组的学生多15人,则参加体育小组的学生与参加科技小组的学生人数之和是 人.
11.2023年4月,北京市每日最高气温的统计图如图所示:
根据统计图提供的信息,有下列三个结论:①若按每日最高气温由高到低排序,4月4日排在第30位;②4月7日到4月8日气温上升幅度最大;③若记4月上旬(1日至10日)的最高气温的方差为,中旬(11日至20日)的最高气温的方差为,下旬(21日至30日)的最高气温的方差为,则.其中所有正确结论的序号是 .
12.人的呼吸离不开氧气.正常情况下,空气中含氧量为21%左右,在扇形统计图中,表示氧气的扇形圆心角是 度.
13.如图是友谊商场某商品1~4月份单个的进价和售价的折线统计图,则售出该商品单个利润最大的是 月份.
14.某工厂第一车间有15名工人,每人日均加工螺杆数统计如图.则该车间工人日均生产螺杆数的中位数是 个,众数是 个.
15.某市各类学校占该市学校总数的百分比如下:
幼儿园 小学 中学 高等院校 其他
若根据这个统计表制作扇形统计图,则“中学”对应的扇形圆心角的度数为 .
16.某校对1000名学生的身高进行了测量,身高在(单位:m)这一小组的频率为0.26,则该组的人数为 .
三、解答题
17.某校为响应“传承楚文化,弘扬屈原精神”主题阅读倡议,随机抽取了八年级若干名学生,对其周末课外阅读时间进行了调查.根据收集到的数据,整理后得到如下不完整的统计图表(每组包含最小值,不包含最大值):
时长(分) 30~60 60~90 90~120 120~150
组中值 ① 75 105 135
频数 6 20 ② 4
数据分组后,一个组的两个端点的数的平均数,叫做这个组的组中值.
请你根据图表中提供的信息,解答下面的问题:
(1)扇形统计图中,120~150分钟时间段对应扇形的圆心角的度数是 °,a的值为 .样本数据的中位数位于 时间段.
(2)请将表格补充完整.
(3)请通过计算估计该校八年级学生周末平均课外阅读时间.
18.某公司要在甲、乙两人中招聘一名职员,对两人的学历、能力、经验这三项进行了测试.各项满分均为10分,成绩高者被录用,图1是甲、乙测试成绩的条形统计图·
(1)分别求出甲、乙三项成绩之和,并指出会录用谁.
(2)将甲、乙的三项测试成绩按照扇形统计图(如图2)各项所占之比,分别计算各自的综合成绩,并判断是否会改变(1)的录用结果
19.某中学为加强学生的劳动教育,需要制定学生每周劳动时间(单位:时)的合格标准,为此随机调查了 100 名学生目前每周劳动时间,获得数据并整理成下表.
每周劳动时间x(时) 0.5≤x<1.5 1.5≤x<2.5 2.5≤x<3.5 3.5≤x<4.5 4.5≤x<5.5
组中值 1 2 3 4 5
人数 21 30 19 18 12
(1)画扇形图描述数据时,1.5≤x<2.5这组数据对应的扇形的圆心角是多少度
(2)估计该校学生目前每周劳动时间的平均数.
(3)请你为该校制定一个学生每周劳动时间的合格标准(时间取整数小时),并用统计量说明其合理性.
20.某中学开展“迎接党的二十大”知识比赛,九年级(1)班、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写表格:
班级 中位数 平均数 众数
九(1)班 85 ? 85
九(2)班 ? 85 ?
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好?说明理由;
(3)如果规定成绩较稳定的班级胜出,你认为哪个班级能胜出?说明理由.
21.某教育局为了解初中毕业年级学生的体质情况,从某校九年级学生中随机抽取20%的学生进行体质监测.根据《中学生体质健康标准》规定学生体质健康等级标准:90分及以上为优秀;80分~89分为良好;60分~79分为及格;60分以下为不及格,将测试成绩制成如下图表.
各等级学生频率分布表
成绩 频数 频率
优秀 16 b
良好 a 0.24
及格 18 0.36
不及格 4 0.08
请根据图表信息回答下列问题:
(1)表格中的a=_ ,b=_ .
(2)已知“80分~89分”这组的数据如下:81,83,84,85,85,81,80,86,87,88,83,85,则所抽取的这些学生体质监测成绩的中位数是 _ .
(3)求参加本次体质监测的学生的平均成绩.
(4)请估计该校九年级体质监测成绩未达到“良好”等级及以上的学生人数.
22.某校对八年级的名学生进行了一次体育测试测试完成后,在甲、乙两班各抽取了名学生的测试成绩,对数据进行整理分析,并给出了下列信息:
甲班名同学的测试成绩统计如下:,,,,,,,,,,,,,,,,,,,.
乙班名同学的测试成绩统计如下:
组别
频数
其中,乙班名同学的测试成绩高于,但不超过分的成绩如下:,,,,,.
甲、乙两班抽取的学生的测试成绩的平均数、中位数、众数如表所示:
班级 平均数 中位数 众数
甲班
乙班
(1)根据以上信息可以写出: , , ;
(2)你认为甲、乙两个班哪个班的学生体育测试成绩较好,请说明理由;
(3)若规定分及以上为优秀,请估计该校八年级参加此次测试的学生中优秀的学生有多少人.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】B
7.【答案】C
8.【答案】D
9.【答案】乙
10.【答案】
11.【答案】①③
12.【答案】75.6
13.【答案】2
14.【答案】14;12
15.【答案】72°
16.【答案】260人
17.【答案】(1)36;25;60~90分钟
(2)①:45,②:10
(3)84分钟
18.【答案】(1)解:由题意得,甲三项成绩之和为:9+5+9=23(分),
乙三项成绩之和为:8+9+5=22(分),
∵23>22,
∴会录用甲;
(2)解:由题意得,甲三项成绩之加权平均数为:(分),
乙三项成绩之加权平均数为:(分),
∵7<8,
∴会改变(1)的录用结果.
19.【答案】(1)解:∵×100%=30%,
∴ 1.5≤x<2.5这组数据对应的扇形的圆心角=360°×30%=108°;
(2)解:=2.7(小时);
(3)解:从平均数看,标准可以定为3小时,理由:平均数为2.7小时,则可知该校学生目前每周劳动时间平均值为27小时,把标准定为3小时,至少有30%的学生每周劳动时间可达标,同时还有至少还有51%的学生未达标,这样使大多数学生有更高的努力的目标.
20.【答案】(1)85、80、100
(2)解:九(1)的复赛成绩较好;
理由:因为两个班的平均数相同,九(1)班的中位数高,所以九(1)班的复赛成绩较好;
(3)解:九(1)班成绩稳定些,能胜出;
理由:,
,
因为,
所以九(1)班成绩稳定些,能胜出.
21.【答案】(1)12;0.32
(2)82
(3)解:=(92×16+84×12+70×18+45×4)÷50=78.4.
答:参加本次体质监测的学生的平均成绩为 78.4.
(4)(4+18)÷20%=110(人).
答:该校九年级体质监测成绩未达到“良好”等级及以上的学生人数约为 110 人
22.【答案】(1)3;48;50
(2)解:甲班的成绩好.
理由:甲乙两班的平均数相等,甲班的中位数和众数都比乙班的大;
(3)解:(人),
答:估计该校八年级参加此次测试的学生中优秀的学生有人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
