鲁教版八年级数学下册第11章11.2图形的旋转同步训练题(含答案)
文档属性
| 名称 | 鲁教版八年级数学下册第11章11.2图形的旋转同步训练题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 176.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-20 00:00:00 | ||
图片预览

文档简介
鲁教版八年级数学下册第11章11.2图形的旋转同步训练题(含答案)
一.选择题(共10小题)
1.(2015春 北京校级月考)在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有( )
A. ①② B. ②③ C. ①④ D. ③④
2.(2015 广州)将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A. B. C. D.
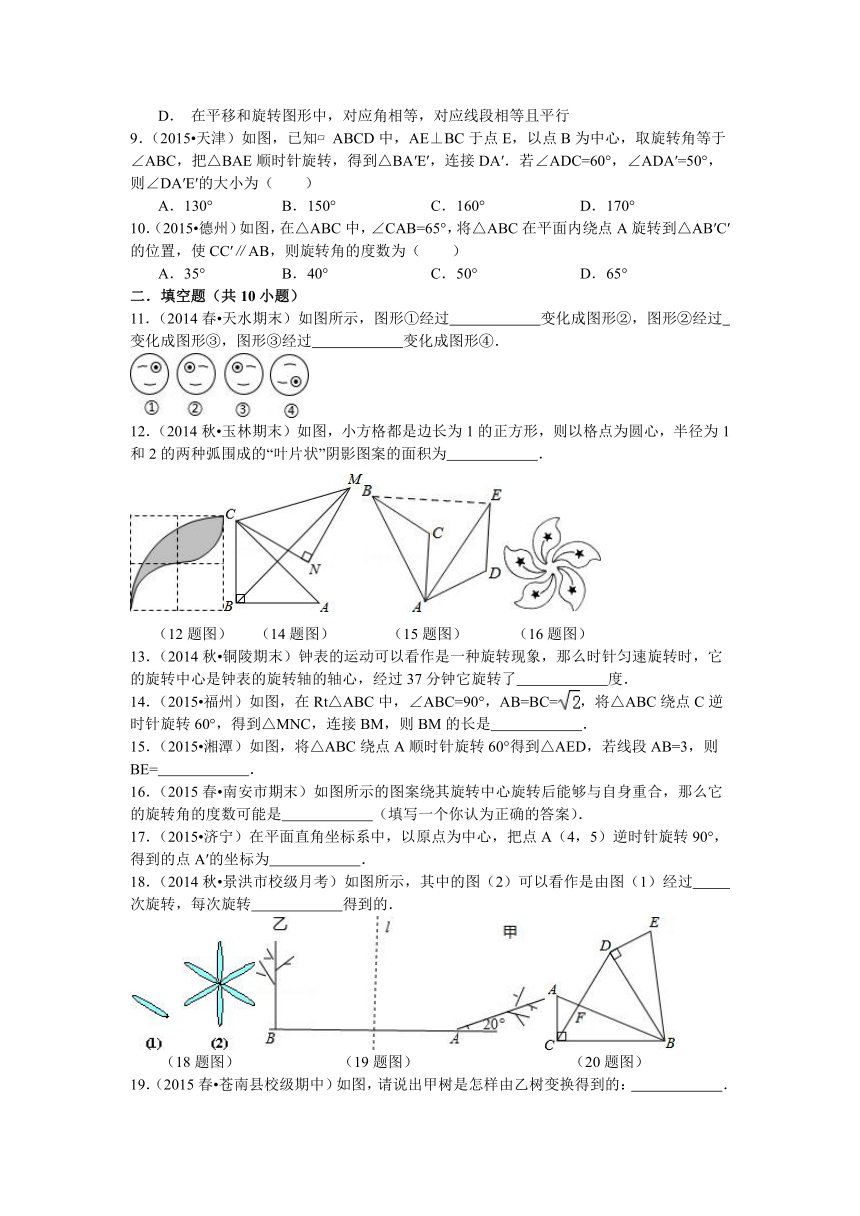
3.(2015 枣庄)如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. B. C. D.﹣1
(3题图) (9题图) (10题图)
4.(2015 浠水县校级模拟)等边三角形ABC绕着它的中心,至少旋转( )度才能与它本身重合.
A.60° B. 120° C. 180° D. 360°
5.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.B. C. D.
6.(2014 怀柔区一模)在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
A.B.C.D.
7.(2014秋 罗平县校级期末)如图所示的图案中,可以由一个“基本图案”连续旋转45°得到的是( )
A. B. C. D.
8.(2015春 长清区期末)下列说法正确的是( )
A. 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B. 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C. 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D. 在平移和旋转图形中,对应角相等,对应线段相等且平行
9.(2015 天津)如图,已知 ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
A.130° B. 150° C. 160° D. 170°
10.(2015 德州)如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.35° B. 40° C. 50° D. 65°
二.填空题(共10小题)
11.(2014春 天水期末)如图所示,图形①经过 变化成图形②,图形②经过 变化成图形③,图形③经过 变化成图形④.
12.(2014秋 玉林期末)如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为 .
(12题图) (14题图) (15题图) (16题图)
13.(2014秋 铜陵期末)钟表的运动可以看作是一种旋转现象,那么时针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过37分钟它旋转了 度.
14.(2015 福州)如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
15.(2015 湘潭)如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= .
16.(2015春 南安市期末)如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是 (填写一个你认为正确的答案).
17.(2015 济宁)在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°,得到的点A′的坐标为 .
18.(2014秋 景洪市校级月考)如图所示,其中的图(2)可以看作是由图(1)经过 次旋转,每次旋转 得到的.
(18题图) (19题图) (20题图)
19.(2015春 苍南县校级期中)如图,请说出甲树是怎样由乙树变换得到的: .
20.(2015 吉林)如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 cm.
三.解答题(共4小题)
21.图中,甲图怎样变成乙图: .
22.(2015 裕华区模拟)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
23.(2015 贵港)如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)请按要求画图:
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
24.(2015 衡阳)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
鲁教版八年级数学下册第11章11.2图形的旋转同步训练题参考答案
一.选择题(共10小题)
1.A 2.D 3.D 4.B 5.C 6.C 7.B 8.B 9.C 10.C
二.填空题(共10小题)
11.轴对称(翻折)平移旋转 12.π-2 13.18.5 14.+1 15.3
16.72°(答案不唯一) 17.(-5,4) 18.560°
19.先以直线L为对称轴作轴对称变换,再把所得的像绕点A顺时针旋转70度 20.42
三.解答题(共4小题)
19、解:观察可知,甲图绕点A顺时针旋转即可变成乙图.
故答案为:绕点A顺时针旋转.
20.(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,∴∠ODC=60°,∴∠ADO=∠ADC﹣∠ODC=90°,
∵∠α=150°∠AOB=110°,∠COD=60°,
∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°,
∴△AOD不是等腰直角三角形,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,∴190°﹣α=α﹣60°,∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°﹣(∠AOD+∠ADO)=180°﹣(190°﹣α+α﹣60°)=50°,∴α﹣60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.∵∠OAD=360°﹣110°﹣60°﹣α=190°﹣α,
∠AOD==120°﹣,∴190°﹣α=120°﹣,解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
21.解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)由图形可知:交点坐标为(﹣1,﹣4).
(21题图) (22题图)
22.解:(1)A(3,2)、B(3,5)、C(1,2)关于x轴的对称点分别为A1(3,﹣2),B1(3,﹣5),C1(1,﹣2),
如图所示,
(2)①∵A(3,2)、B(3,5)、C(1,2),
∴AB=3,AC=2,BC=,
∵,∴AB2+AC2=BC2,∴∠CAB=90°,
∵AC与AC2的夹角为∠CAC2,∴旋转角为90°;
②∵AB=AB2=3,∴CB2=AC+AB2=5,∴B2的坐标为(6,2).
一.选择题(共10小题)
1.(2015春 北京校级月考)在下列现象中:①时针转动,②电风扇叶片的转动,③转呼啦圈,④传送带上的电视机,其中是旋转的有( )
A. ①② B. ②③ C. ①④ D. ③④
2.(2015 广州)将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
A. B. C. D.
3.(2015 枣庄)如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )
A. B. C. D.﹣1
(3题图) (9题图) (10题图)
4.(2015 浠水县校级模拟)等边三角形ABC绕着它的中心,至少旋转( )度才能与它本身重合.
A.60° B. 120° C. 180° D. 360°
5.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是( )
A.B. C. D.
6.(2014 怀柔区一模)在下列某品牌T恤的四个洗涤说明图案的设计中,没有运用旋转或轴对称知识的是( )
A.B.C.D.
7.(2014秋 罗平县校级期末)如图所示的图案中,可以由一个“基本图案”连续旋转45°得到的是( )
A. B. C. D.
8.(2015春 长清区期末)下列说法正确的是( )
A. 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B. 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化
C. 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D. 在平移和旋转图形中,对应角相等,对应线段相等且平行
9.(2015 天津)如图,已知 ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,∠ADA′=50°,则∠DA′E′的大小为( )
A.130° B. 150° C. 160° D. 170°
10.(2015 德州)如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A.35° B. 40° C. 50° D. 65°
二.填空题(共10小题)
11.(2014春 天水期末)如图所示,图形①经过 变化成图形②,图形②经过 变化成图形③,图形③经过 变化成图形④.
12.(2014秋 玉林期末)如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为 .
(12题图) (14题图) (15题图) (16题图)
13.(2014秋 铜陵期末)钟表的运动可以看作是一种旋转现象,那么时针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过37分钟它旋转了 度.
14.(2015 福州)如图,在Rt△ABC中,∠ABC=90°,AB=BC=,将△ABC绕点C逆时针旋转60°,得到△MNC,连接BM,则BM的长是 .
15.(2015 湘潭)如图,将△ABC绕点A顺时针旋转60°得到△AED,若线段AB=3,则BE= .
16.(2015春 南安市期末)如图所示的图案绕其旋转中心旋转后能够与自身重合,那么它的旋转角的度数可能是 (填写一个你认为正确的答案).
17.(2015 济宁)在平面直角坐标系中,以原点为中心,把点A(4,5)逆时针旋转90°,得到的点A′的坐标为 .
18.(2014秋 景洪市校级月考)如图所示,其中的图(2)可以看作是由图(1)经过 次旋转,每次旋转 得到的.
(18题图) (19题图) (20题图)
19.(2015春 苍南县校级期中)如图,请说出甲树是怎样由乙树变换得到的: .
20.(2015 吉林)如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则△ACF与△BDF的周长之和为 cm.
三.解答题(共4小题)
21.图中,甲图怎样变成乙图: .
22.(2015 裕华区模拟)如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
23.(2015 贵港)如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).
(1)请按要求画图:
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.
(2)请写出直线B1C1与直线B2C2的交点坐标.
24.(2015 衡阳)如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C(1,2).
(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;
(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.
①旋转角为多少度?
②写出点B2的坐标.
鲁教版八年级数学下册第11章11.2图形的旋转同步训练题参考答案
一.选择题(共10小题)
1.A 2.D 3.D 4.B 5.C 6.C 7.B 8.B 9.C 10.C
二.填空题(共10小题)
11.轴对称(翻折)平移旋转 12.π-2 13.18.5 14.+1 15.3
16.72°(答案不唯一) 17.(-5,4) 18.560°
19.先以直线L为对称轴作轴对称变换,再把所得的像绕点A顺时针旋转70度 20.42
三.解答题(共4小题)
19、解:观察可知,甲图绕点A顺时针旋转即可变成乙图.
故答案为:绕点A顺时针旋转.
20.(1)证明:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,∴CO=CD,∠OCD=60°,
∴△COD是等边三角形.
(2)解:当α=150°时,△AOD是直角三角形.
理由是:∵将△BOC绕点C按顺时针方向旋转60°得△ADC,∴△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,∴∠ODC=60°,∴∠ADO=∠ADC﹣∠ODC=90°,
∵∠α=150°∠AOB=110°,∠COD=60°,
∴∠AOD=360°﹣∠α﹣∠AOB﹣∠COD=360°﹣150°﹣110°﹣60°=40°,
∴△AOD不是等腰直角三角形,即△AOD是直角三角形.
(3)解:①要使AO=AD,需∠AOD=∠ADO,
∵∠AOD=360°﹣110°﹣60°﹣α=190°﹣α,∠ADO=α﹣60°,∴190°﹣α=α﹣60°,∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠OAD=180°﹣(∠AOD+∠ADO)=180°﹣(190°﹣α+α﹣60°)=50°,∴α﹣60°=50°,
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.∵∠OAD=360°﹣110°﹣60°﹣α=190°﹣α,
∠AOD==120°﹣,∴190°﹣α=120°﹣,解得α=140°.
综上所述:当α的度数为125°或110°或140°时,△AOD是等腰三角形.
21.解:(1)如图所示:△A1B1C1即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)由图形可知:交点坐标为(﹣1,﹣4).
(21题图) (22题图)
22.解:(1)A(3,2)、B(3,5)、C(1,2)关于x轴的对称点分别为A1(3,﹣2),B1(3,﹣5),C1(1,﹣2),
如图所示,
(2)①∵A(3,2)、B(3,5)、C(1,2),
∴AB=3,AC=2,BC=,
∵,∴AB2+AC2=BC2,∴∠CAB=90°,
∵AC与AC2的夹角为∠CAC2,∴旋转角为90°;
②∵AB=AB2=3,∴CB2=AC+AB2=5,∴B2的坐标为(6,2).
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
