2023-2024学年高中数学人教A版选择性必修第三册第五章计数原理重难点检测卷(含答案)
文档属性
| 名称 | 2023-2024学年高中数学人教A版选择性必修第三册第五章计数原理重难点检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-05 09:06:29 | ||
图片预览



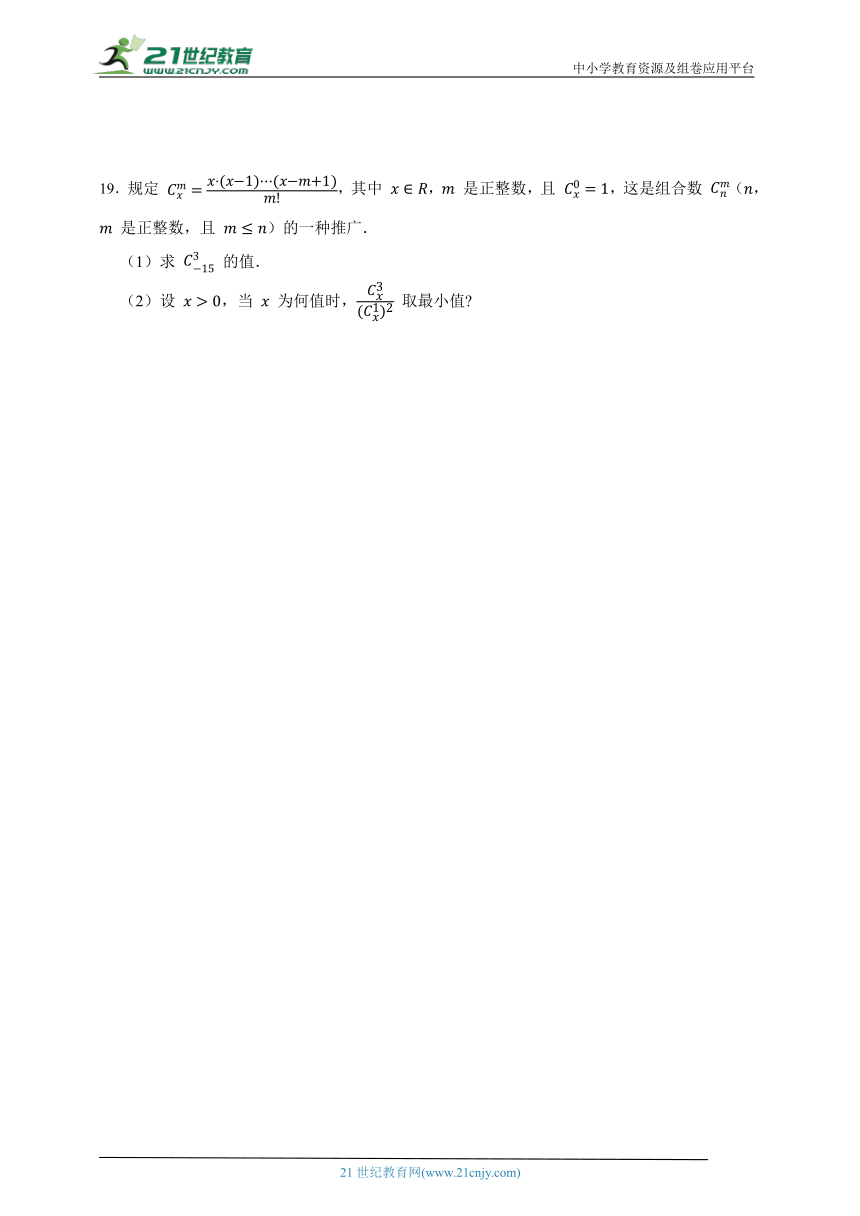
文档简介
中小学教育资源及组卷应用平台
2023-2024学年高中数学人教A版选择性必修第三册第五章计数原理重难点检测卷
一、选择题
1.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
2.从一副不含大、小王的52张扑克牌中任意抽出5张,则至少有3张是A的概率为( )
A. B.
C. D.
3.设 ,,则 的值为( )
A.128 B.129 C.47 D.0
4.已知 的展开式中 项的系数与 项的系数分别为 135 与-18,则 的展开式中所有项系数之和为( )
A.-1 B.1 C.32 D.64
5. 的展开式中的常数项为( )
A.32 B.34 C.36 D.38
6.已知 ,则 ( )
A.63 B.64 C.31 D.32
7. 的展开式中, 的奇次幂的系数之和是( )
A.2048 B.-1023 C.-1024 D.1024
8.在二项式 的展开式中,所有二项式系数的和是32,则展开式中各项系数的和为( )
A.32 B.-32 C.0 D.1
二、多项选择题
9.如图,在一广场两侧设置6只彩灯,现有4种不同颜色的彩灯可供选择,则下列结论正确的是( )
A.共有种不同方案
B.若相邻两灯不同色,正相对的两灯(如1 4)也不同色,且4种颜色的彩灯均要使用,则共有186种不同方案
C.若相邻两灯不同色,正相对的两灯(如1 4)也不同色,且只能使用3种颜色的彩灯,则共有192种不同方案
D.若相邻两灯不同色,正相对的两灯(如1 4)也不同色,且只能使用2种颜色的彩灯,则共有12种不同方案
10.为了贯彻常态化疫情防控工作,动员广大医护人员抓细抓实各项防疫工作,人民医院组织护理、感染、儿科、疾控、药剂、呼吸六位专家进行“防疫有我,健康同行”知识讲座,每天一人,连续6天.则下列结论正确的是( )
A.从六位专家中选两位的不同选法共有20种
B.“呼吸类专家”不排在最后一天的不同排法共有600种
C.“护理、感染类专家”排在相邻两天的不同排法共有240种
D.“护理、感染、儿科类专家”排在都不相邻的三天的不同排法共有72种
11.若的二项展开式共有9项,则该二项展开式( )
A.各项二项式系数和为256
B.项数为奇数的各项系数和为
C.有理项共有5项
D.第5项系数最大
三、填空题
12. 的展开式中, 的系数等于 (用数字作答).
13. .
14.若将函数 表示成 ,则 的值等于 .
四、解答题
15. 现有一批产品共有10件,其中8件为正品,2件为次品:
(1) 如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2) 如果从中一次取3件,求3件都是正品的概率.
16.求和:.
17.已知 ().
(1)若其展开式后三项的二项式系数的和等于
,求展开式中二项式系数最大的项;
(2)若 为满足 的整数,且展开式中有常数项,试求 的值和常数项.
18.若 ,
(1)求 的值;
(2)求 的值;
(3)求 的值.
19.规定 ,其中 , 是正整数,且 ,这是组合数 (, 是正整数,且 )的一种推广.
(1)求 的值.
(2)设 ,当 为何值时, 取最小值
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】D
8.【答案】C
9.【答案】A,C,D
10.【答案】B,C
11.【答案】A,C,D
12.【答案】120
13.【答案】
14.【答案】20
15.【答案】(1)解:有放回的抽取3次,那么每次抽取都有10种可能,因此共有种可能。 连续3次都取正品共有种可能,因此 如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率为
(2)解:如果从中一次取3件 ,可以看作不放回抽样3次,则易知第一次有10种可能,第二次有9种可能,第一次有8种可能,所以事件总数为,
“三件都是正品”,第一次抽中正品有8种可能,第一次基础上第二次抽中正品有7种可能,同理,第三次抽中正品有6种可能,所以三件都是正品得可能有种,
故 如果从中一次取3件,求3件都是正品的概率为.
16.【答案】解: =
=
=
=
17.【答案】(1)解:由已知得 ,
整理得 ,即 ,解得 或 (舍去).
则 ,其展开式中二项式系数最大的项为第 项和第 项,
即 ,
(2)解: 的展开式的通项为 .
设第 项为常数项,则有 ,即 ,
所以 ,即 ,
又 ,所以 或 ,
当 时, ;
当 时, (不合题意,舍去),
所以 ,即当 时,展开式中有常数项,
常数项为 .
18.【答案】(1)解:求二项展开式中各项系数之和,相当于去掉展开式中的未知字母 ,这可由赋值法令 实现.则
(2)解:若要求二项展开式中奇数项系数之和,可由赋值法令 ,
则
将①,②两式相加得: ,
则
(3)解:将①,②两式相减得: ,
则
19.【答案】(1)解:
(2)解: .
因为 ,
所以 ,当且仅当 时,等号成立.
所以,当 时, 取得最小值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年高中数学人教A版选择性必修第三册第五章计数原理重难点检测卷
一、选择题
1.安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
2.从一副不含大、小王的52张扑克牌中任意抽出5张,则至少有3张是A的概率为( )
A. B.
C. D.
3.设 ,,则 的值为( )
A.128 B.129 C.47 D.0
4.已知 的展开式中 项的系数与 项的系数分别为 135 与-18,则 的展开式中所有项系数之和为( )
A.-1 B.1 C.32 D.64
5. 的展开式中的常数项为( )
A.32 B.34 C.36 D.38
6.已知 ,则 ( )
A.63 B.64 C.31 D.32
7. 的展开式中, 的奇次幂的系数之和是( )
A.2048 B.-1023 C.-1024 D.1024
8.在二项式 的展开式中,所有二项式系数的和是32,则展开式中各项系数的和为( )
A.32 B.-32 C.0 D.1
二、多项选择题
9.如图,在一广场两侧设置6只彩灯,现有4种不同颜色的彩灯可供选择,则下列结论正确的是( )
A.共有种不同方案
B.若相邻两灯不同色,正相对的两灯(如1 4)也不同色,且4种颜色的彩灯均要使用,则共有186种不同方案
C.若相邻两灯不同色,正相对的两灯(如1 4)也不同色,且只能使用3种颜色的彩灯,则共有192种不同方案
D.若相邻两灯不同色,正相对的两灯(如1 4)也不同色,且只能使用2种颜色的彩灯,则共有12种不同方案
10.为了贯彻常态化疫情防控工作,动员广大医护人员抓细抓实各项防疫工作,人民医院组织护理、感染、儿科、疾控、药剂、呼吸六位专家进行“防疫有我,健康同行”知识讲座,每天一人,连续6天.则下列结论正确的是( )
A.从六位专家中选两位的不同选法共有20种
B.“呼吸类专家”不排在最后一天的不同排法共有600种
C.“护理、感染类专家”排在相邻两天的不同排法共有240种
D.“护理、感染、儿科类专家”排在都不相邻的三天的不同排法共有72种
11.若的二项展开式共有9项,则该二项展开式( )
A.各项二项式系数和为256
B.项数为奇数的各项系数和为
C.有理项共有5项
D.第5项系数最大
三、填空题
12. 的展开式中, 的系数等于 (用数字作答).
13. .
14.若将函数 表示成 ,则 的值等于 .
四、解答题
15. 现有一批产品共有10件,其中8件为正品,2件为次品:
(1) 如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2) 如果从中一次取3件,求3件都是正品的概率.
16.求和:.
17.已知 ().
(1)若其展开式后三项的二项式系数的和等于
,求展开式中二项式系数最大的项;
(2)若 为满足 的整数,且展开式中有常数项,试求 的值和常数项.
18.若 ,
(1)求 的值;
(2)求 的值;
(3)求 的值.
19.规定 ,其中 , 是正整数,且 ,这是组合数 (, 是正整数,且 )的一种推广.
(1)求 的值.
(2)设 ,当 为何值时, 取最小值
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】A
7.【答案】D
8.【答案】C
9.【答案】A,C,D
10.【答案】B,C
11.【答案】A,C,D
12.【答案】120
13.【答案】
14.【答案】20
15.【答案】(1)解:有放回的抽取3次,那么每次抽取都有10种可能,因此共有种可能。 连续3次都取正品共有种可能,因此 如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率为
(2)解:如果从中一次取3件 ,可以看作不放回抽样3次,则易知第一次有10种可能,第二次有9种可能,第一次有8种可能,所以事件总数为,
“三件都是正品”,第一次抽中正品有8种可能,第一次基础上第二次抽中正品有7种可能,同理,第三次抽中正品有6种可能,所以三件都是正品得可能有种,
故 如果从中一次取3件,求3件都是正品的概率为.
16.【答案】解: =
=
=
=
17.【答案】(1)解:由已知得 ,
整理得 ,即 ,解得 或 (舍去).
则 ,其展开式中二项式系数最大的项为第 项和第 项,
即 ,
(2)解: 的展开式的通项为 .
设第 项为常数项,则有 ,即 ,
所以 ,即 ,
又 ,所以 或 ,
当 时, ;
当 时, (不合题意,舍去),
所以 ,即当 时,展开式中有常数项,
常数项为 .
18.【答案】(1)解:求二项展开式中各项系数之和,相当于去掉展开式中的未知字母 ,这可由赋值法令 实现.则
(2)解:若要求二项展开式中奇数项系数之和,可由赋值法令 ,
则
将①,②两式相加得: ,
则
(3)解:将①,②两式相减得: ,
则
19.【答案】(1)解:
(2)解: .
因为 ,
所以 ,当且仅当 时,等号成立.
所以,当 时, 取得最小值
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
