2023-2024学年高中数学人教A版选择性必修第三册第六章随机变量及其分布重难点检测卷(含答案)
文档属性
| 名称 | 2023-2024学年高中数学人教A版选择性必修第三册第六章随机变量及其分布重难点检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-04 21:20:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2023-2024学年高中数学人教A版选择性必修第三册第六章随机变量及其分布重难点检测卷
一、选择题
1.从分别写有1,2,3的三张卡片中随机抽取一张,放回后再随机抽取一张,连续抽取4次,则恰好有2次抽到的卡片上的数字为奇数的概率为( )
A. B. C. D.
2.某班有48名同学,一次考试后各位同学的数学成绩服从正态分布,平均分为80,标准差为10,则理论上来说在80分到90分间的人数是( )
A.32 B.16 C.8 D.20
3.某地市高三理科学生有15000名,在一次调研测试中,数学成绩ξ服从正态公布N(100,σ^2),已知P(80<ξ≤100)=0.40,若按成绩分层抽样的方式取100份试卷分析,则应从120分以上的试卷中抽取( )
A.5份 B.10份 C.15份 D.20份
4.已知随机变量服从正态分布,若,则( )
A.0.477 B.0.625
C.0.977 D.0.954
5.在某次数学测试中,学生成绩ξ服从正态分布N(100,σ^2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
6.设随机变量,且落在区间内的概率和落在区间内的概率相等,若,则等于( )
A. B. C. D.
7.一只袋内装有m个白球,n-m个黑球,连续不放回地从袋中取球,直到取出黑球为止,设此时取出了X个白球,下列概率等于的是( )
A. B. C. D.
8.已知变量服从正态分布,下列概率与相等的是( )
A. B. C. D.
二、多项选择题
9.已知事件,满足,且,则一定有( )
A. B.
C. D.
10.对于离散型随机变量 的数学期望 和方差 ,下列说法正确的是( )
A. 反映随机变量的平均取值
B. 越小,说明 越集中于
C.
D.
11.下列关于说法正确的是( )
A.抛掷均匀硬币一次,出现正面的次数是随机变量
B.某人射击时命中的概率为0.5,此人射击三次命中的次数 服从两点分布
C.小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件 “4个人去的景点不相同”,事件 “小赵独自去一个景点”,则
D.已知随机变量 服从两点分布,且 , ,令 ,则
三、填空题
12.若随机变量,且,则
13.设随机变量,若,则 .
14.在某项测量中,测量结果服从正态分布.若在内取值的概率为,则在内取值的概率为 .
四、解答题
15.某食品厂生产了一批罐头,每罐标准净重是340克.由于生产条件限制,每罐的净重并非恰好340克.已知每罐的净重服从正态分布,从这一批罐头中随机取出100罐进行检查,测得数据如下(单位:克):
经计算,这个样本的平均数和标准差分别为
(克),(克).
试估计:
(1)这批罐头中,净重不超过340克的罐头所占的百分比.
(2)这批罐头中,净重在克与克,即克克之间的罐头所占的百分比.
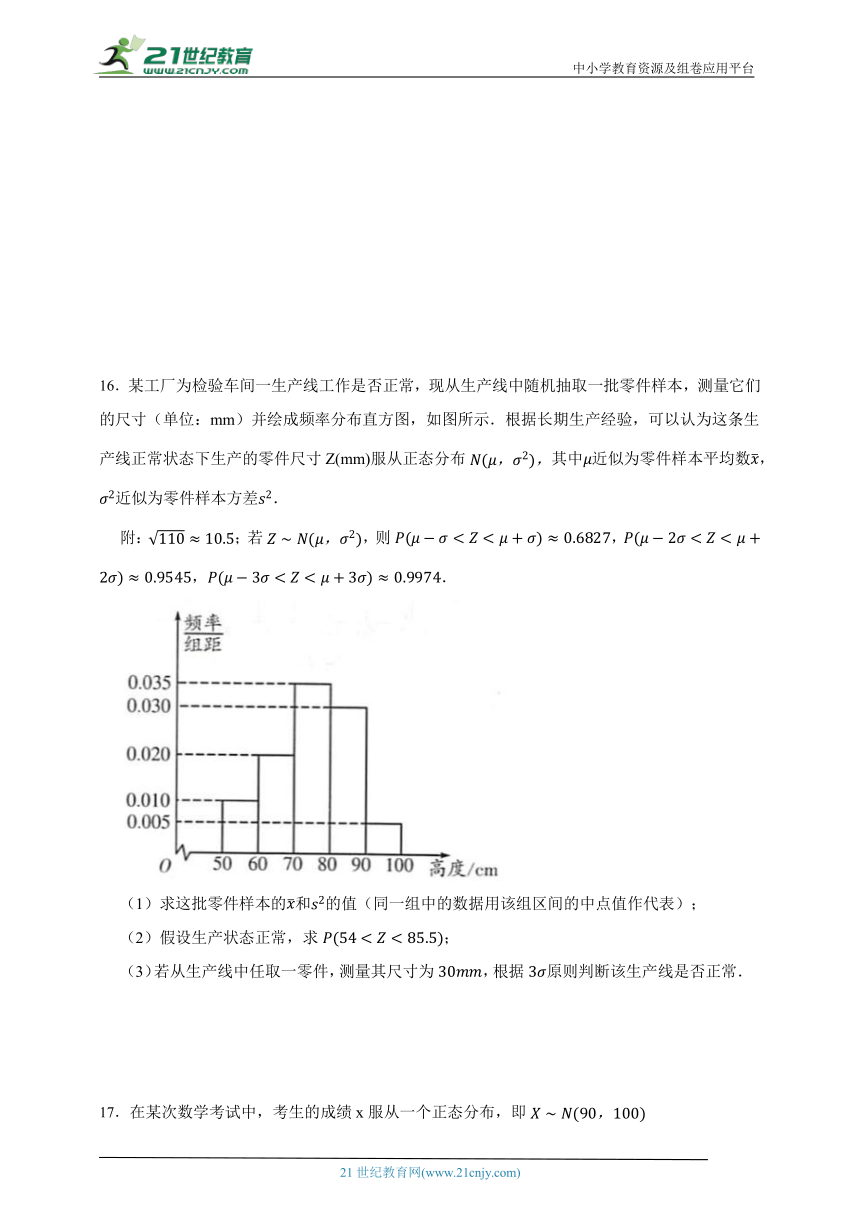
16.某工厂为检验车间一生产线工作是否正常,现从生产线中随机抽取一批零件样本,测量它们的尺寸(单位:mm)并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸Z(mm)服从正态分布其中近似为零件样本平均数,近似为零件样本方差.
附:;若,则,,.
(1)求这批零件样本的和的值(同一组中的数据用该组区间的中点值作代表);
(2)假设生产状态正常,求;
(3)若从生产线中任取一零件,测量其尺寸为,根据原则判断该生产线是否正常.
17.在某次数学考试中,考生的成绩x服从一个正态分布,即
(1)求考试成绩x位于区间内的概率
(2)若这次考试共有2000名考生,试估计考试成绩在内的考生大约有多少人
18.某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大
19.箱中装有4个白球和m个黑球.规定取出一个白球得2分,取出一个黑球得1分,现从箱中任取3个球,假设每个球被取出的可能性都相等.记随机变量X为取出的3个球所得分之和.
(1)若,求的值;
(2)当时,求x的分布列.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】B,C
10.【答案】A,B,C
11.【答案】A,C,D
12.【答案】0.842
13.【答案】0.7
14.【答案】0.8
15.【答案】(1)解:因为,
所以,
所以这批罐头中,净重不超过340克的罐头所占的百分比;
(2) 所以这批罐头中,净重在克与克,即克克之间的罐头所占的百分比约为0.951.
16.【答案】(1)解:由题意可得平均数 ,
(2)解:因为 ,
所以 .
从而 .
,
所以
(3)解: , .
因为 ,
所以该生产线工作不正常
17.【答案】(1)解:因为 ,所以 , .
因为正态变量在区间 内取值的概率是 ,而该正态分布中, , ,
所以考试成绩 位于区间 内的概率是
(2)解:由 , ,得 ,
因为正态变量在区间 内取值的概率是 ,
所以考试成绩 位于区间 内的概率是
因为一共有2000名考生,
所以考试成绩在 内的考生大约有 (人)
18.【答案】(1)解:设甲正确完成面试的题数为 ,则 的可能取值为 , , .
; ; .
应聘者甲正确完成题数 的分布列为
设乙正确完成面试的题数为 ,则 的可能取值为 , , , .
; ;
;
.
应聘者乙正确完成题数 的分布列为
(或因为 ,
所以 )
(2)解:因为 , .
所以 .
综上所述,从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;从至少完成 道题的概率考查,甲面试通过的可能性大
19.【答案】(1)解:由题意得,只有当取出的 个球都是白球时,随机变量 ,
所以 ,即 ,
所以 .
(2)解:由题意得,当 时, 的可能取值为3,4,5,6
, , , .
所以 的分布列为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年高中数学人教A版选择性必修第三册第六章随机变量及其分布重难点检测卷
一、选择题
1.从分别写有1,2,3的三张卡片中随机抽取一张,放回后再随机抽取一张,连续抽取4次,则恰好有2次抽到的卡片上的数字为奇数的概率为( )
A. B. C. D.
2.某班有48名同学,一次考试后各位同学的数学成绩服从正态分布,平均分为80,标准差为10,则理论上来说在80分到90分间的人数是( )
A.32 B.16 C.8 D.20
3.某地市高三理科学生有15000名,在一次调研测试中,数学成绩ξ服从正态公布N(100,σ^2),已知P(80<ξ≤100)=0.40,若按成绩分层抽样的方式取100份试卷分析,则应从120分以上的试卷中抽取( )
A.5份 B.10份 C.15份 D.20份
4.已知随机变量服从正态分布,若,则( )
A.0.477 B.0.625
C.0.977 D.0.954
5.在某次数学测试中,学生成绩ξ服从正态分布N(100,σ^2)(σ>0),若ξ在(80,120)内的概率为0.8,则ξ在(0,80)内的概率为( )
A.0.05 B.0.1 C.0.15 D.0.2
6.设随机变量,且落在区间内的概率和落在区间内的概率相等,若,则等于( )
A. B. C. D.
7.一只袋内装有m个白球,n-m个黑球,连续不放回地从袋中取球,直到取出黑球为止,设此时取出了X个白球,下列概率等于的是( )
A. B. C. D.
8.已知变量服从正态分布,下列概率与相等的是( )
A. B. C. D.
二、多项选择题
9.已知事件,满足,且,则一定有( )
A. B.
C. D.
10.对于离散型随机变量 的数学期望 和方差 ,下列说法正确的是( )
A. 反映随机变量的平均取值
B. 越小,说明 越集中于
C.
D.
11.下列关于说法正确的是( )
A.抛掷均匀硬币一次,出现正面的次数是随机变量
B.某人射击时命中的概率为0.5,此人射击三次命中的次数 服从两点分布
C.小赵、小钱、小孙、小李到4个景点旅游,每人只去一个景点,设事件 “4个人去的景点不相同”,事件 “小赵独自去一个景点”,则
D.已知随机变量 服从两点分布,且 , ,令 ,则
三、填空题
12.若随机变量,且,则
13.设随机变量,若,则 .
14.在某项测量中,测量结果服从正态分布.若在内取值的概率为,则在内取值的概率为 .
四、解答题
15.某食品厂生产了一批罐头,每罐标准净重是340克.由于生产条件限制,每罐的净重并非恰好340克.已知每罐的净重服从正态分布,从这一批罐头中随机取出100罐进行检查,测得数据如下(单位:克):
经计算,这个样本的平均数和标准差分别为
(克),(克).
试估计:
(1)这批罐头中,净重不超过340克的罐头所占的百分比.
(2)这批罐头中,净重在克与克,即克克之间的罐头所占的百分比.
16.某工厂为检验车间一生产线工作是否正常,现从生产线中随机抽取一批零件样本,测量它们的尺寸(单位:mm)并绘成频率分布直方图,如图所示.根据长期生产经验,可以认为这条生产线正常状态下生产的零件尺寸Z(mm)服从正态分布其中近似为零件样本平均数,近似为零件样本方差.
附:;若,则,,.
(1)求这批零件样本的和的值(同一组中的数据用该组区间的中点值作代表);
(2)假设生产状态正常,求;
(3)若从生产线中任取一零件,测量其尺寸为,根据原则判断该生产线是否正常.
17.在某次数学考试中,考生的成绩x服从一个正态分布,即
(1)求考试成绩x位于区间内的概率
(2)若这次考试共有2000名考生,试估计考试成绩在内的考生大约有多少人
18.某公司为招聘新员工设计了一个面试方案:应聘者从6道备选题中一次性随机抽取3道题,按照题目要求独立完成.规定:至少正确完成其中2道题的便可通过.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列及数学期望;
(2)请分析比较甲、乙两人谁面试通过的可能性大
19.箱中装有4个白球和m个黑球.规定取出一个白球得2分,取出一个黑球得1分,现从箱中任取3个球,假设每个球被取出的可能性都相等.记随机变量X为取出的3个球所得分之和.
(1)若,求的值;
(2)当时,求x的分布列.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】B
9.【答案】B,C
10.【答案】A,B,C
11.【答案】A,C,D
12.【答案】0.842
13.【答案】0.7
14.【答案】0.8
15.【答案】(1)解:因为,
所以,
所以这批罐头中,净重不超过340克的罐头所占的百分比;
(2) 所以这批罐头中,净重在克与克,即克克之间的罐头所占的百分比约为0.951.
16.【答案】(1)解:由题意可得平均数 ,
(2)解:因为 ,
所以 .
从而 .
,
所以
(3)解: , .
因为 ,
所以该生产线工作不正常
17.【答案】(1)解:因为 ,所以 , .
因为正态变量在区间 内取值的概率是 ,而该正态分布中, , ,
所以考试成绩 位于区间 内的概率是
(2)解:由 , ,得 ,
因为正态变量在区间 内取值的概率是 ,
所以考试成绩 位于区间 内的概率是
因为一共有2000名考生,
所以考试成绩在 内的考生大约有 (人)
18.【答案】(1)解:设甲正确完成面试的题数为 ,则 的可能取值为 , , .
; ; .
应聘者甲正确完成题数 的分布列为
设乙正确完成面试的题数为 ,则 的可能取值为 , , , .
; ;
;
.
应聘者乙正确完成题数 的分布列为
(或因为 ,
所以 )
(2)解:因为 , .
所以 .
综上所述,从做对题数的数学期望考查,两人水平相当;从做对题数的方差考查,甲较稳定;从至少完成 道题的概率考查,甲面试通过的可能性大
19.【答案】(1)解:由题意得,只有当取出的 个球都是白球时,随机变量 ,
所以 ,即 ,
所以 .
(2)解:由题意得,当 时, 的可能取值为3,4,5,6
, , , .
所以 的分布列为
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
