江苏省2024届中考数学一轮模拟卷(二)(含解析)
文档属性
| 名称 | 江苏省2024届中考数学一轮模拟卷(二)(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
江苏省2024届中考数学一轮模拟卷(二)
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.的倒数是( )
A.2023 B. C. D.
2.型口罩能过滤空气中95%的粒径约为 m的非油性颗粒.用科学记数法表示是( )
A. B. C. D.
3.一组数据:2,4,4,4,6,若去掉一个数据4,则下列统计量中发生变化的是( )
A.众数 B.中位数 C.平均数 D.方差
4.下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了解某灯管的使用寿命,可以采用普查的方式进行
C.两组身高数据的方差分别是0.01,0.02,那么乙组的身高比较整齐
D.一组数据3,5,4,5,6,7的众数、中位数和平均数都是5
5.如图,在平面直角坐标系中,菱形的边在轴的正半轴上,反比例函数的图象经过对角线的中点和顶点.若菱形的面积为12,则的值为( ).
A.6 B.5 C.4 D.3
6.如图,点A,B,C均在上,当时,的度数是( )
A.25° B.30° C.40° D.50°
7.关于x的一元二次方程有实数根,则k的值可以是( )
A.4 B.5 C.6 D.7
8.如图,矩形中, ,动点P从点A出发向终点D运动,连,并过点C作,垂足为H.① ;②的最小值为 ; ③在运动过程中,点H的运动路径的长为 , 其中正确的有( )
A.①②③ B.①② C.②③ D.①③
二、填空题
9.我国钓鱼诸岛面积约6344000平方米,数据6344000用科学记数法表示为 .
10.因式分解: .
11.关于的一元二次方程没有实数根,则的取值范围是 .
12.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x … ﹣3 ﹣1 1 3 …
y … ﹣4 2 4 2 …
则当﹣3<x<3时,y满足的范围是 .
13.口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
14.如图,直线,的直角顶点C在直线b上,若,则的度数为 .
15.已知圆锥的母线长为12,底面圆的半径为6,则圆锥的侧面积是 .
16.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,
连接CD.若CD=AC,∠A=50°,则∠ACB .
17.如图,在正十边形中,连接、,则 °
18.已知二次函数(为常数).点,,在二次函数的图像上,当时,的取值范围是 .
三、解答题
19.计算:.
20.解不等式组:
21.为了解学生对校园安全知识的掌握情况,现从九年级随机选取甲、乙两组各20名同学组织一次测试,并对本次测试成绩(满分为分)进行统计学处理:
【收集数据】甲组名同学的成绩统计数据:(单位:分)
乙组名同学中成绩在分之间数据:(满分为分,得分用x表示,单位:分)
【整理数据】(得分用表示)
(1)完成下表
分数/班级
甲班(人数)
乙班(人数)
【分析数据】请回答下列问题:
(2)填空:
平均分 中位数 众数
甲班
乙班
(3)若成绩不低于分为优秀,请以甲组、乙组共人为样本估计全年级人中优秀人数为多少?
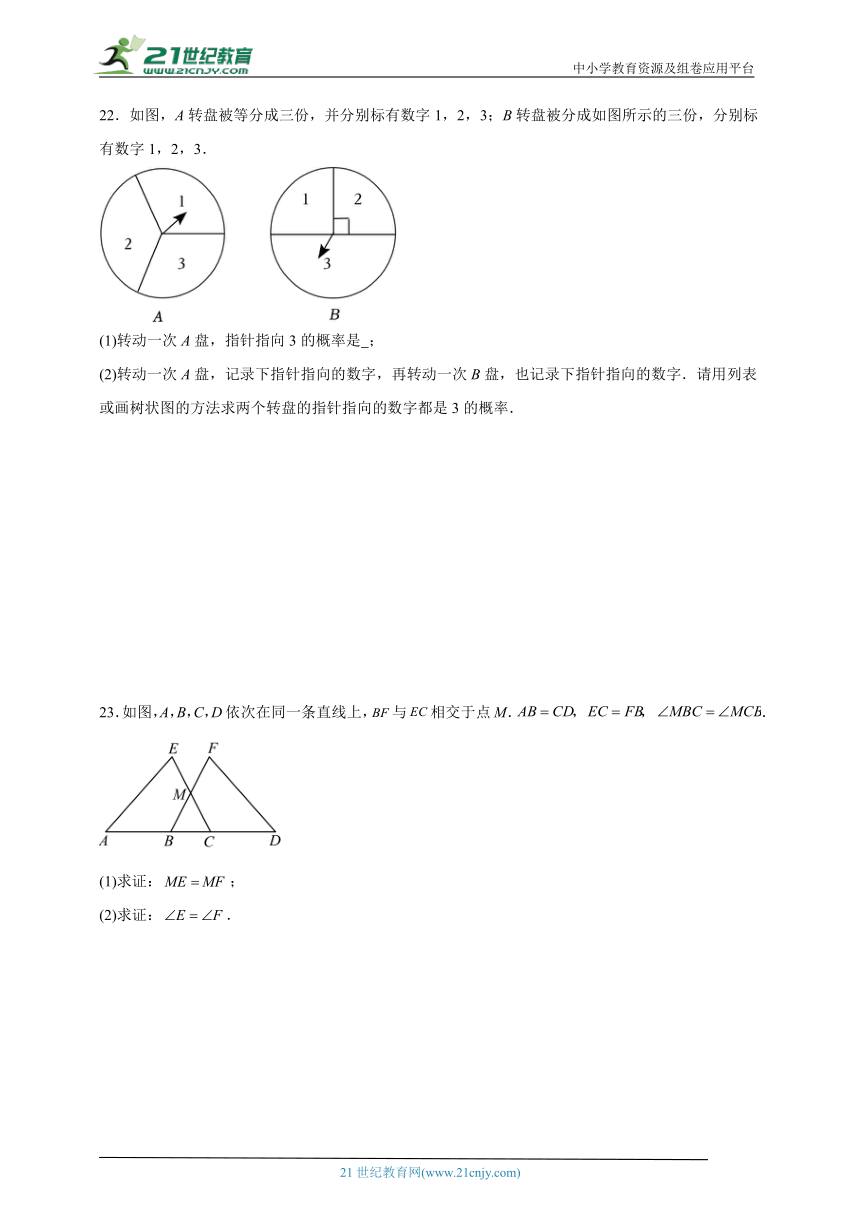
22.如图,A转盘被等分成三份,并分别标有数字1,2,3;B转盘被分成如图所示的三份,分别标有数字1,2,3.
(1)转动一次A盘,指针指向3的概率是 ;
(2)转动一次A盘,记录下指针指向的数字,再转动一次B盘,也记录下指针指向的数字.请用列表或画树状图的方法求两个转盘的指针指向的数字都是3的概率.
23.如图,A,B,C,D依次在同一条直线上,与相交于点M..
(1)求证:;
(2)求证:.
24.某餐饮公司推出甲、乙两种外卖菜品,已知售出2份甲菜品和1份乙菜品可获利40元,售出3份甲菜品和2份乙菜品可获利65元.
(1)求每份甲、乙菜品的利润各是多少元?
(2)根据营销情况,该餐饮公司每日都可以销售完甲、乙两种外卖菜品600份,且甲菜品的数量不多于乙菜品的一半,应该如何设计两种菜品的数量才能使获得的利润最高?最高利润是多少?
25.在某张航海图上,标明了三个观测点的坐标,如图,,,,由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东29°,求观测点B到A船的距离(结果精确到0.1,参考数据:,,).
26.如图,一次函数与反比例函数第一象限交于、两点,点是轴负半轴上一动点,连接,.
(1)求一次函数的表达式;
(2)若的面积为,求点的坐标;
(3)在(2)的条件下,若点为直线上一点,点为轴上一点,是否存在这样的点和点,使得四边形是平行四边形?若存在,直接写出点的坐标;若不存在,请说明理由.
27.如图,已知抛物线经过点,,与轴交于点.
(1)求抛物线的解析式;
(2)若点为该抛物线上一动点.
①当点在直线下方时,过点作轴,交直线于点,作轴.交直线于点,求的最大值;
②若,求点的横坐标.
28.问题提出:
(1)“弦图”是中国古代数学成就的一个重要标志.小明用边长为的正方形制作了一个“弦图”:如图①,在正方形内取一点,使得,作,,垂足分别为、,延长交于点.若,求的长;
变式应用:
(2)如图②,分别以正方形的边长和为斜边向内作和,连接,若已知,,的面积为,,则正方形的面积为 .
拓展应用:
(3)如图③,公园中有一块四边形空地,米,米,米,,空地中有一段半径为米的弧形道路(即),现准备在上找一点将弧形道路改造为三条直路(即、、),并要求,三条直路将空地分割为、和四边形三个区域,用来种植不同的花草.
①则的度数为 ;
②求四边形的面积.
参考答案:
1.B
【分析】根据倒数的定义,进行求解即可.
【详解】解:的倒数是
故选B.
【点睛】本题考查了倒数,熟练掌握互为倒数的两数之积为1,是解题的关键.
2.D
【分析】科学记数法的表现形式为的形式,其中,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数;由此进行求解即可得到答案.
【详解】解:,
故选D.
【点睛】本题主要考查了科学记数法,解题的关键在于能够熟练掌握科学记数法的定义.
3.D
【分析】根据众数、中位数、平均数及方差可直接进行排除选项.
【详解】解:由题意得:
原中位数为4,原众数为4,原平均数为,原方差为;
去掉一个数据4后的中位数为,众数为4,平均数为,方差为;
∴统计量发生变化的是方差;
故选D.
【点睛】本题主要考查平均数、众数、众数及方差,熟练掌握求一组数据的平均数、众数及方差是解题的关键.
4.D
【分析】A.根据生活实际判断事件是否必然发生进行判断即可;
B.当调查具有破坏性或费时费力时一般采用抽样调查;
C.根据方差意义,方差越小,数据越整齐,即可做出判断;
D.分别求出数据的众数,中位数,平均数即可判断.
【详解】A.清明节有可能下雨,也可能不下雨,所以“清明时节雨纷纷”是随机事件,故A错误;
B.调查某灯管的使用寿命,具有破坏性,应采用抽样调查的方式,故B错误;
C.∵<,
∴甲组的身高比较整齐,故C错误;
D.将数据排序为:3,4,5,5,6,7,中间两个数都是5,因此中位数是5,这组数据中出现次数最多的是5,因此众数是5,这组数据的平均数为,故D正确.
故选:D.
【点睛】本题考查了必然事件和随机事件、全面调查和抽样调查、方差的意义、平均数、中位数、众数的计算,内容较多,熟知统计调查、众数、中位数的基本概念、方差的意义是解题关键.
5.C
【分析】首先设出A、C点的坐标,再根据菱形的性质可得D点坐标,再根据D点在反比例函数上,再结合面积等于12,解方程即可.
【详解】解:设点的坐标为,点的坐标为,
则,点的坐标为,
∴,
解得,,
故选C.
【点睛】本题主要考查反比例函数和菱形的性质,关键在于菱形的对角线相互平分且垂直.
6.C
【分析】根据等腰三角形的性质,可得,得出,再根据圆周角定理,得,即可得解.
【详解】解:点A,B,C均在上,,
,
,
,
,
;
故选C.
【点睛】此题考查了圆的性质、圆周角定理、三角形内角和定理与等腰三角形判定与性质,熟练掌握并运用相关性质是解此题的关键.
7.A
【分析】利用一元二次方程根的判别式求解即可.
【详解】解:∵关于x的一元二次方程有实数根,
∴,
∴,
∴四个选项中只有A选项符合题意,
故选A.
【点睛】本题主要考查了一元二次方程根的判别式,对于一元二次方程,若,则方程有两个不相等的实数根,若,则方程有两个相等的实数根,若,则方程没有实数根.
8.A
【分析】根据矩形的性质和垂直的定义得到,再由三角形内角和定理证明,可证△ABP∽△HCB;如图1所示,取的中点O,连接则,可得点H在以O为圆心,以的长为直径的圆上运动,则当在同一直线上时,最短;根据点H的运动路线(轨迹)为,运用弧长公式即可得出结果.
【详解】解:∵,
∴,
∵四边形是矩形,
∴,,
∴,
∵,
,故①正确;
如图1所示,取的中点O,连接则,
∵,
∴,
∴点H在以O为圆心,以的长为直径的圆上运动,
∴当在同一直线上时,最短,
此时,
∴的最小值为,故②正确;
如图2所示,在运动过程中,点H的运动轨迹即为,
在中,,
∵,
∴,
∴,
∴是等边三角形,
∴,
∴
∴点H的运动路线(轨迹)长为,故③正确;
故选A.
【点睛】本题主要考查了圆外一点到圆上一点的最值问题,相似三角形的性质与判定,矩形的性质,求弧长,等边三角形的性质与判定,勾股定理得到,正确推出点H的运动轨迹是解题的关键.
9.
【分析】根据科学记数法的表示形式即可得出答案.
【详解】解:6344000=,
故答案为:.
【点睛】本题考查了科学记数法,解题关键熟练掌握科学记数法的表示形式.
10.
【分析】先提公因式,再用平方差公式分解.
【详解】解:
【点睛】本题考查因式分解,掌握因式分解方法是关键.
11.
【分析】根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于的不等式,解不等式即可,同时还应注意二次项系数不能为0.
【详解】解:由题意可知:,
,
故答案为:.
【点睛】本题主要考查了一元二次方程根的判别式,解题关键是掌握根的判别式如何决定一元二次方程根的情况.
12.﹣4<y≤4
【分析】利用二次函数图象上点的坐标特征可根据x=﹣3及x=3时y的值,结合二次函数图象的顶点坐标,即可找出﹣3<x<3时y的取值范围.
【详解】解:从表格看出,函数的对称轴为x=1,顶点为(1,4),函数有最大值4,
∴抛物线开口向下,
∴当﹣3<x<3时,﹣4<y≤4,
故答案为,﹣4<y≤4.
【点睛】本题考查了二次函数的性质,二次函数图象上点的坐标特征,解题的关键是学会看懂表格信息,灵活运用所学知识解决问题,属于基础题.
13.0.3.
【详解】试题解析:根据概率公式摸出黑球的概率是1-0.2-0.5=0.3.
考点:概率公式.
14.50°/50度
【分析】如图:由平行线的性质可得,然后根据平角的性质可得即可求得.
【详解】解:∵,
∴,
∵,
∴.
故答案为50°.
【点睛】本题主要考查了平行线的性质、平角的定义等知识点,熟记性质并准确识图是解题的关键.
15.
【分析】直接根据圆的周长公式求出圆锥侧面展开图扇形的弧长,然后由扇形面积计算即可.
【详解】由题意可知:圆锥的底面周长为,即圆锥侧面展开扇形的弧长为,
则圆锥的侧面积.
故答案为:.
【点睛】本题考查了圆锥的计算,解决的关键是理解圆锥的母线长是圆锥侧面展开图扇形的半径,圆锥的底面周长是扇形的弧长.
16.105°/105度
【分析】根据作图可知MN垂直平分BC,由垂直平分线的性质,等腰三角形的性质,三角形内角和180°,进行角度计算即可解答;
【详解】解:由作图步骤可知MN是BC的垂直平分线,
,
,,
,
,
,,
.
故答案为:105°.
【点睛】本题考查了:线段垂直平分线上的点到这条线段两个端点的距离相等;等腰三角形等边对等角;三角形内角和定理;掌握相关性质和定理是解题关键.
17.54
【分析】设正十边形的圆心O,连接A7O、A4O,再求出∠A7OA4,最后运用圆周角定理解答即可.
【详解】解:如图:设正十边形的圆心O,连接A7O、A4O,
∵正十边形的各边都相等
∴∠A7OA4=×360°=108°
∴108°×=54°.
故填54.
【点睛】本题主要考查了正多边形和圆以及圆周角定理,根据题意正确作出辅助线、构造出圆周角是解答本题的关键.
18.或0≤m≤2或m≥3
【分析】分别求出y1,y2,y3,利用y1 y2 y3≥0,得出关于m的不等式,求出m的值即可.
【详解】由题意可知,y1=(1-m)(1-m-2)=(m-1)(m+1),
y2=(2-m)(2-m-2)=m(m-2),
y3=(3-m)(3-m-2)=(m-1)(m-3),
∵y1 y2 y30,
∴(m-1)(m+1) m (m-2) (m-1)(m-3)≥0,即m(m+1)(m-2)(m-3)(m-1)20,
∵(m-1)2≥0,
∴m,(m+1),(m-2),(m-3)的负数有偶数个,且m+1>m>m-2>m-3,
当负数有4个时,m+10,
∴m;
当负数有2个时,m-20且m0,
∴,
当负数有0个时,,
∴
∴m的取值范围为:.
故答案为:
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,数形结合解题是关键.
19.
【分析】利用立方根的意义,零指数幂法则,负整数指数幂运算法则将原式化简,再进行加减运算即可.
【详解】解:
.
【点睛】本题考查实数的运算.掌握立方根的意义,零指数幂法则,负整数指数幂运算法则是解题的关键.
20.
【分析】先分别求出两个不等式的解集,再根据夹逼原则求出不等式组的解集即可.
【详解】解:解不等式得:,
解不等式得:,
∴不等式组的解集为.
【点睛】本题主要考查了解一元一次不等式组,正确求出每个一元一次不等式的解集是解题的关键.
21.(1),
(2),
(3)人
【分析】(1)根据数据统计的方法以及各组数据之和等于样本容量可得答案;
(2)根据中位数、众数的定义可求出、的值;
(3)求出样本中甲乙两个班“优秀”所占的百分比,进而估计总体中“优秀”所占的百分比,再乘总人数即可.
【详解】(1)解:由题意可知,乙班在的数据有个,在的有,个,
故答案为:,;
(2)甲班人中得分出现次数最多的是分,共出现次,因此甲班学生成绩的众数,
将乙班名学生的成绩从小到大排列,处在中间位置的两个数的平均数为,因此中位数,
故答案为:,;
(3)(人),
答:甲班、乙班共人为样本估计全年级人中优秀人数约为人.
【点睛】本题考查中位数、众数,频数分布表,掌握中位数、众数以及“频率”是正确解答的前提.
22.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中两个转盘的指针指向的数字都是3的结果有2种,再由概率公式求解即可.
【详解】(1)解:转动一次A盘,指针指向3的概率是,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果,其中两个转盘的指针指向的数字都是3的结果有2种,
∴两个转盘的指针指向的数字都是3的概率为:.
【点睛】本题考查树状图法求概率,树状图法可以不重不漏的列举出所有可能发生的情况,适合于两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
23.(1)见解析
(2)见解析
【分析】(1)先证明,由全等三角形的性质可得,然后根据可得,最后根据等量代换即可证明结论;
(2)直接运用全等三角形对应角相等的性质即可证明结论.
【详解】(1)证明:∵,
∴,即,
在和中,
,
∴,
∴,
又∵,
∴,
∴.
(2)证明:∵,
∴.
【点睛】本题主要考查了全等三角形的判定与性质,证得是解答本题的关键.
24.(1)每份菜品甲的利润为15元,每份菜品乙的利润为10元
(2)购进甲菜品200份,乙菜品400份,所获利润最大,最大利润为7000元
【分析】(1)设每份菜品甲的利润为元,每份菜品乙的利润为元,根据售出2份甲菜品和1份乙菜品可获利40元,售出3份甲菜品和2份乙菜品可获利65元,列二元一次方程组,求解即可;
(2)设销售甲菜品份,总利润为元,根据甲菜品的数量不多于乙菜品的一半,求出的取值范围,再表示出与的函数关系式,根据一次函数的增减性即可确定最大利润时进货方案,进一步求出最大利润即可.
【详解】(1)解:设每份菜品甲的利润为元,每份菜品乙的利润为元,
根据题意,得:,
解得:,
答:每份菜品甲的利润为15元,每份菜品乙的利润为10元;
(2)设销售甲菜品份,总利润为元,
根据题意,得:,
解得:,
,
∵,
∴随着的增大而增大,
当时,取得最大值,最大值为:(元),
此时销售乙菜品:(份),
答:销售甲菜品200份,乙菜品400份,所获利润最大,最大利润为7000元.
【点睛】本题考查一次函数的应用,二元一次方程组的应用,一元一次不等式的应用,理解题意是解题的关键.
25.(1)
(2)15.5
【分析】(1)根据题意可以求得圆心的坐标和圆的半径,从而可以求得圆形区域的面积;
(2)过点A作轴于点D,依题意,得,在中,设,则,由,根据图形得到则,解方程求得x,进而解直角三角形求得
【详解】(1)连接,则轴,
∴,
设为由O、B、C三点所确定圆的圆心,
则为的直径,
由已知得,由勾股定理得,
∴半径,
∴;
(2)过点A作轴于点D,依题意,得,
在中,设,
则,
∴,
∴,
由题意得:,
则,
解得:,
在中,有,即,
∴
【点睛】本题考查了勾股定理的应用、解直角三角形以及圆的面积计算等知识.熟练掌握圆由半径和圆心确定是解答本题的关键.
26.(1)
(2)
(3)存在,
【分析】(1)用待定系数法即可求解;
(2)由,即可求解;
(3)是平行四边形的边,且点向右平移个单位向下平移个单位得到点,则点向右平移个单位向下平移个单位得到点,进而求解.
【详解】(1)解:∵点在反比例函数图像上,
∴,
∴反比例函数的表达式为,
当时,,
∴,
∵,在一次函数图像上,
∴,
解得:,
∴一次函数的表达式为;
(2)设直线交轴于点,
当时,,解得:
∴点,
设点,
∵的面积为,
∴,
∴,
解得:,
∴点的坐标为;
(3)存在,理由:
设直线的解析式为,,,
∴,
解得:,
直线的解析式为,
设点,
∵是平行四边形的边,且点向右平移个单位向下平移个单位得到点,点在轴上,
∴点向右平移个单位向下平移个单位得到点,
∴
∴,
∴点的坐标为.
【点睛】本题是反比例函数综合题,考查了待定系数法求函数解析式,三角形面积,平行四边形性质等,解题关键是运用点坐标平移的规律:左减右加纵不变,上加下减横不变解决问题.
27.(1)
(2)①;②
【分析】(1)用待定系数法即可求解;
(2)①由直线的表达式知,其和轴负半轴的夹角为,即,则,进而求解;
②作点关于轴的对称点,则,用解直角三角形的方法求出,进而求解.
【详解】(1)解:∵抛物线经过点,,
∴,
解得:,
∴抛物线的解析式为;
(2)①∵抛物线的解析式为,
当时,,
∴,
设直线的解析式为,,,
∴,
解得:,
∴直线的解析式为,
设点,点,
∴,
∵,
∴当时,的最大值为,
∵,,
∴,
∴,
∵轴,作轴,
∴,,
∴,,
∴,
∴的最大值为;
②作点关于轴的对称点,连接、,
∴垂直平分,
∴,
∴,
∵,
∴,
过点作于点,
∴,
∴,
∴,
∴,
∴,
设直线与轴交于点,
∴,
∴,
当点在轴的正半轴时,,
设直线的解析式为,,,
∴,
解得:,
∴直线的解析式为,
∵点在抛物线上,
∴,
解得:(此时是钝角,不合题意,舍去),(舍去),
当点在轴的负半轴时,,
设直线的解析式为,,,
∴,
解得:,
∴直线的解析式为,
∵点在抛物线上,
∴,
解得:,(舍去),
综上所述,点的横坐标为.
【点睛】本题是二次函数的综合题,考查了运用待定系数法求函数的解析式,二次函数与一次函数的交点坐标,对称的性质,平行线的性质,等角对等边,三角形内角和,勾股定理,三角函数定义的应用,二次函数的最值等知识点,运用了分类讨论和等积法的思想.解题关键是正确添加辅助线构造等角和等积法的运用.
28.(1);(2);(3)①;②平方米
【分析】(1)根据矩形的判定定理得到四边形是矩形,求得,根据正方形的性质得到,,根据全等三角形的性质得到,根据勾股定理即可得到结论;
(2)如图②,延长交于,延长交于,根据全等三角形的性质得到,,求得,根据余角的性质得到,同理,,根据全等三角形的性质得到,求得正方形的面积,于是得到结论;
(3)①如图③,连接,根据勾股定理得到,根据勾股定理的逆定理得到,推出是所在圆的直径,是等腰直角三角形,得到点,,,四点共圆,,圆内接四边形的性质得到的度数;
②根据三角形的面积公式得到;根据旋转的想得到,,,延长交于,推出是等腰直角三角形,得到,根据勾股定理和三角形的面积公式即可得到结论.
【详解】解:∵,,,
∴,
∴四边形是矩形,
∴,
∴,
∵四边形是正方形,
∴,,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴,
解得:或(负值不合题意,舍去),
∴的长为;
(2)解:如图②,延长交于,延长交于,
∵四边形是正方形,
∴,
∵,,
在和中,
,
∴,
∴,,,
∵,
∴,
∴,
∴,
∴,
同理,,
在和中,
,
∴,
∴,,
在和中,
,
∴,
∴,,
∴,,
∴,
∴四边形是正方形,
∵的面积为,,
∴正方形的面积为:,
∴正方形的面积为:,
故答案为:;
(3)如图③,连接,
∵,,
∴,
∵,,
∴,
∴,
∴是所在圆的直径,是等腰直角三角形,
∴点,,,四点共圆,,
∴,
∴,
故答案为:;
②∵是等腰直角三角形,
∴,
把绕着点逆时针旋转,得到,
∴,,,
∴∠,,
∴,
∴,
延长交于,
∴,,
∴是等腰直角三角形,,
∴,,
∴,
∵,
∴四边形是正方形,
∴,
∴,
∵,
∴,
∴,
∴
,
∴(平方米).
【点睛】本题是圆的综合题,考查旋转的性质,全等三角形的判定和性质,正方形的判定和性质,等腰直角三角形的判定和性质,圆周角定理,勾股定理,勾股定理的逆定理,正确地作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
江苏省2024届中考数学一轮模拟卷(二)
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.的倒数是( )
A.2023 B. C. D.
2.型口罩能过滤空气中95%的粒径约为 m的非油性颗粒.用科学记数法表示是( )
A. B. C. D.
3.一组数据:2,4,4,4,6,若去掉一个数据4,则下列统计量中发生变化的是( )
A.众数 B.中位数 C.平均数 D.方差
4.下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了解某灯管的使用寿命,可以采用普查的方式进行
C.两组身高数据的方差分别是0.01,0.02,那么乙组的身高比较整齐
D.一组数据3,5,4,5,6,7的众数、中位数和平均数都是5
5.如图,在平面直角坐标系中,菱形的边在轴的正半轴上,反比例函数的图象经过对角线的中点和顶点.若菱形的面积为12,则的值为( ).
A.6 B.5 C.4 D.3
6.如图,点A,B,C均在上,当时,的度数是( )
A.25° B.30° C.40° D.50°
7.关于x的一元二次方程有实数根,则k的值可以是( )
A.4 B.5 C.6 D.7
8.如图,矩形中, ,动点P从点A出发向终点D运动,连,并过点C作,垂足为H.① ;②的最小值为 ; ③在运动过程中,点H的运动路径的长为 , 其中正确的有( )
A.①②③ B.①② C.②③ D.①③
二、填空题
9.我国钓鱼诸岛面积约6344000平方米,数据6344000用科学记数法表示为 .
10.因式分解: .
11.关于的一元二次方程没有实数根,则的取值范围是 .
12.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x … ﹣3 ﹣1 1 3 …
y … ﹣4 2 4 2 …
则当﹣3<x<3时,y满足的范围是 .
13.口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么摸出黑球的概率是 .
14.如图,直线,的直角顶点C在直线b上,若,则的度数为 .
15.已知圆锥的母线长为12,底面圆的半径为6,则圆锥的侧面积是 .
16.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,
连接CD.若CD=AC,∠A=50°,则∠ACB .
17.如图,在正十边形中,连接、,则 °
18.已知二次函数(为常数).点,,在二次函数的图像上,当时,的取值范围是 .
三、解答题
19.计算:.
20.解不等式组:
21.为了解学生对校园安全知识的掌握情况,现从九年级随机选取甲、乙两组各20名同学组织一次测试,并对本次测试成绩(满分为分)进行统计学处理:
【收集数据】甲组名同学的成绩统计数据:(单位:分)
乙组名同学中成绩在分之间数据:(满分为分,得分用x表示,单位:分)
【整理数据】(得分用表示)
(1)完成下表
分数/班级
甲班(人数)
乙班(人数)
【分析数据】请回答下列问题:
(2)填空:
平均分 中位数 众数
甲班
乙班
(3)若成绩不低于分为优秀,请以甲组、乙组共人为样本估计全年级人中优秀人数为多少?
22.如图,A转盘被等分成三份,并分别标有数字1,2,3;B转盘被分成如图所示的三份,分别标有数字1,2,3.
(1)转动一次A盘,指针指向3的概率是 ;
(2)转动一次A盘,记录下指针指向的数字,再转动一次B盘,也记录下指针指向的数字.请用列表或画树状图的方法求两个转盘的指针指向的数字都是3的概率.
23.如图,A,B,C,D依次在同一条直线上,与相交于点M..
(1)求证:;
(2)求证:.
24.某餐饮公司推出甲、乙两种外卖菜品,已知售出2份甲菜品和1份乙菜品可获利40元,售出3份甲菜品和2份乙菜品可获利65元.
(1)求每份甲、乙菜品的利润各是多少元?
(2)根据营销情况,该餐饮公司每日都可以销售完甲、乙两种外卖菜品600份,且甲菜品的数量不多于乙菜品的一半,应该如何设计两种菜品的数量才能使获得的利润最高?最高利润是多少?
25.在某张航海图上,标明了三个观测点的坐标,如图,,,,由三个观测点确定的圆形区域是海洋生物保护区.
(1)求圆形区域的面积;
(2)某时刻海面上出现渔船A,在观测点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东29°,求观测点B到A船的距离(结果精确到0.1,参考数据:,,).
26.如图,一次函数与反比例函数第一象限交于、两点,点是轴负半轴上一动点,连接,.
(1)求一次函数的表达式;
(2)若的面积为,求点的坐标;
(3)在(2)的条件下,若点为直线上一点,点为轴上一点,是否存在这样的点和点,使得四边形是平行四边形?若存在,直接写出点的坐标;若不存在,请说明理由.
27.如图,已知抛物线经过点,,与轴交于点.
(1)求抛物线的解析式;
(2)若点为该抛物线上一动点.
①当点在直线下方时,过点作轴,交直线于点,作轴.交直线于点,求的最大值;
②若,求点的横坐标.
28.问题提出:
(1)“弦图”是中国古代数学成就的一个重要标志.小明用边长为的正方形制作了一个“弦图”:如图①,在正方形内取一点,使得,作,,垂足分别为、,延长交于点.若,求的长;
变式应用:
(2)如图②,分别以正方形的边长和为斜边向内作和,连接,若已知,,的面积为,,则正方形的面积为 .
拓展应用:
(3)如图③,公园中有一块四边形空地,米,米,米,,空地中有一段半径为米的弧形道路(即),现准备在上找一点将弧形道路改造为三条直路(即、、),并要求,三条直路将空地分割为、和四边形三个区域,用来种植不同的花草.
①则的度数为 ;
②求四边形的面积.
参考答案:
1.B
【分析】根据倒数的定义,进行求解即可.
【详解】解:的倒数是
故选B.
【点睛】本题考查了倒数,熟练掌握互为倒数的两数之积为1,是解题的关键.
2.D
【分析】科学记数法的表现形式为的形式,其中,n为整数,确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同,当原数绝对值大于等于10时,n是正数,当原数绝对值小于1时n是负数;由此进行求解即可得到答案.
【详解】解:,
故选D.
【点睛】本题主要考查了科学记数法,解题的关键在于能够熟练掌握科学记数法的定义.
3.D
【分析】根据众数、中位数、平均数及方差可直接进行排除选项.
【详解】解:由题意得:
原中位数为4,原众数为4,原平均数为,原方差为;
去掉一个数据4后的中位数为,众数为4,平均数为,方差为;
∴统计量发生变化的是方差;
故选D.
【点睛】本题主要考查平均数、众数、众数及方差,熟练掌握求一组数据的平均数、众数及方差是解题的关键.
4.D
【分析】A.根据生活实际判断事件是否必然发生进行判断即可;
B.当调查具有破坏性或费时费力时一般采用抽样调查;
C.根据方差意义,方差越小,数据越整齐,即可做出判断;
D.分别求出数据的众数,中位数,平均数即可判断.
【详解】A.清明节有可能下雨,也可能不下雨,所以“清明时节雨纷纷”是随机事件,故A错误;
B.调查某灯管的使用寿命,具有破坏性,应采用抽样调查的方式,故B错误;
C.∵<,
∴甲组的身高比较整齐,故C错误;
D.将数据排序为:3,4,5,5,6,7,中间两个数都是5,因此中位数是5,这组数据中出现次数最多的是5,因此众数是5,这组数据的平均数为,故D正确.
故选:D.
【点睛】本题考查了必然事件和随机事件、全面调查和抽样调查、方差的意义、平均数、中位数、众数的计算,内容较多,熟知统计调查、众数、中位数的基本概念、方差的意义是解题关键.
5.C
【分析】首先设出A、C点的坐标,再根据菱形的性质可得D点坐标,再根据D点在反比例函数上,再结合面积等于12,解方程即可.
【详解】解:设点的坐标为,点的坐标为,
则,点的坐标为,
∴,
解得,,
故选C.
【点睛】本题主要考查反比例函数和菱形的性质,关键在于菱形的对角线相互平分且垂直.
6.C
【分析】根据等腰三角形的性质,可得,得出,再根据圆周角定理,得,即可得解.
【详解】解:点A,B,C均在上,,
,
,
,
,
;
故选C.
【点睛】此题考查了圆的性质、圆周角定理、三角形内角和定理与等腰三角形判定与性质,熟练掌握并运用相关性质是解此题的关键.
7.A
【分析】利用一元二次方程根的判别式求解即可.
【详解】解:∵关于x的一元二次方程有实数根,
∴,
∴,
∴四个选项中只有A选项符合题意,
故选A.
【点睛】本题主要考查了一元二次方程根的判别式,对于一元二次方程,若,则方程有两个不相等的实数根,若,则方程有两个相等的实数根,若,则方程没有实数根.
8.A
【分析】根据矩形的性质和垂直的定义得到,再由三角形内角和定理证明,可证△ABP∽△HCB;如图1所示,取的中点O,连接则,可得点H在以O为圆心,以的长为直径的圆上运动,则当在同一直线上时,最短;根据点H的运动路线(轨迹)为,运用弧长公式即可得出结果.
【详解】解:∵,
∴,
∵四边形是矩形,
∴,,
∴,
∵,
,故①正确;
如图1所示,取的中点O,连接则,
∵,
∴,
∴点H在以O为圆心,以的长为直径的圆上运动,
∴当在同一直线上时,最短,
此时,
∴的最小值为,故②正确;
如图2所示,在运动过程中,点H的运动轨迹即为,
在中,,
∵,
∴,
∴,
∴是等边三角形,
∴,
∴
∴点H的运动路线(轨迹)长为,故③正确;
故选A.
【点睛】本题主要考查了圆外一点到圆上一点的最值问题,相似三角形的性质与判定,矩形的性质,求弧长,等边三角形的性质与判定,勾股定理得到,正确推出点H的运动轨迹是解题的关键.
9.
【分析】根据科学记数法的表示形式即可得出答案.
【详解】解:6344000=,
故答案为:.
【点睛】本题考查了科学记数法,解题关键熟练掌握科学记数法的表示形式.
10.
【分析】先提公因式,再用平方差公式分解.
【详解】解:
【点睛】本题考查因式分解,掌握因式分解方法是关键.
11.
【分析】根据方程根的情况可以判定其根的判别式的取值范围,进而可以得到关于的不等式,解不等式即可,同时还应注意二次项系数不能为0.
【详解】解:由题意可知:,
,
故答案为:.
【点睛】本题主要考查了一元二次方程根的判别式,解题关键是掌握根的判别式如何决定一元二次方程根的情况.
12.﹣4<y≤4
【分析】利用二次函数图象上点的坐标特征可根据x=﹣3及x=3时y的值,结合二次函数图象的顶点坐标,即可找出﹣3<x<3时y的取值范围.
【详解】解:从表格看出,函数的对称轴为x=1,顶点为(1,4),函数有最大值4,
∴抛物线开口向下,
∴当﹣3<x<3时,﹣4<y≤4,
故答案为,﹣4<y≤4.
【点睛】本题考查了二次函数的性质,二次函数图象上点的坐标特征,解题的关键是学会看懂表格信息,灵活运用所学知识解决问题,属于基础题.
13.0.3.
【详解】试题解析:根据概率公式摸出黑球的概率是1-0.2-0.5=0.3.
考点:概率公式.
14.50°/50度
【分析】如图:由平行线的性质可得,然后根据平角的性质可得即可求得.
【详解】解:∵,
∴,
∵,
∴.
故答案为50°.
【点睛】本题主要考查了平行线的性质、平角的定义等知识点,熟记性质并准确识图是解题的关键.
15.
【分析】直接根据圆的周长公式求出圆锥侧面展开图扇形的弧长,然后由扇形面积计算即可.
【详解】由题意可知:圆锥的底面周长为,即圆锥侧面展开扇形的弧长为,
则圆锥的侧面积.
故答案为:.
【点睛】本题考查了圆锥的计算,解决的关键是理解圆锥的母线长是圆锥侧面展开图扇形的半径,圆锥的底面周长是扇形的弧长.
16.105°/105度
【分析】根据作图可知MN垂直平分BC,由垂直平分线的性质,等腰三角形的性质,三角形内角和180°,进行角度计算即可解答;
【详解】解:由作图步骤可知MN是BC的垂直平分线,
,
,,
,
,
,,
.
故答案为:105°.
【点睛】本题考查了:线段垂直平分线上的点到这条线段两个端点的距离相等;等腰三角形等边对等角;三角形内角和定理;掌握相关性质和定理是解题关键.
17.54
【分析】设正十边形的圆心O,连接A7O、A4O,再求出∠A7OA4,最后运用圆周角定理解答即可.
【详解】解:如图:设正十边形的圆心O,连接A7O、A4O,
∵正十边形的各边都相等
∴∠A7OA4=×360°=108°
∴108°×=54°.
故填54.
【点睛】本题主要考查了正多边形和圆以及圆周角定理,根据题意正确作出辅助线、构造出圆周角是解答本题的关键.
18.或0≤m≤2或m≥3
【分析】分别求出y1,y2,y3,利用y1 y2 y3≥0,得出关于m的不等式,求出m的值即可.
【详解】由题意可知,y1=(1-m)(1-m-2)=(m-1)(m+1),
y2=(2-m)(2-m-2)=m(m-2),
y3=(3-m)(3-m-2)=(m-1)(m-3),
∵y1 y2 y30,
∴(m-1)(m+1) m (m-2) (m-1)(m-3)≥0,即m(m+1)(m-2)(m-3)(m-1)20,
∵(m-1)2≥0,
∴m,(m+1),(m-2),(m-3)的负数有偶数个,且m+1>m>m-2>m-3,
当负数有4个时,m+10,
∴m;
当负数有2个时,m-20且m0,
∴,
当负数有0个时,,
∴
∴m的取值范围为:.
故答案为:
【点睛】本题考查二次函数的图象及性质,熟练掌握二次函数的图象及性质,数形结合解题是关键.
19.
【分析】利用立方根的意义,零指数幂法则,负整数指数幂运算法则将原式化简,再进行加减运算即可.
【详解】解:
.
【点睛】本题考查实数的运算.掌握立方根的意义,零指数幂法则,负整数指数幂运算法则是解题的关键.
20.
【分析】先分别求出两个不等式的解集,再根据夹逼原则求出不等式组的解集即可.
【详解】解:解不等式得:,
解不等式得:,
∴不等式组的解集为.
【点睛】本题主要考查了解一元一次不等式组,正确求出每个一元一次不等式的解集是解题的关键.
21.(1),
(2),
(3)人
【分析】(1)根据数据统计的方法以及各组数据之和等于样本容量可得答案;
(2)根据中位数、众数的定义可求出、的值;
(3)求出样本中甲乙两个班“优秀”所占的百分比,进而估计总体中“优秀”所占的百分比,再乘总人数即可.
【详解】(1)解:由题意可知,乙班在的数据有个,在的有,个,
故答案为:,;
(2)甲班人中得分出现次数最多的是分,共出现次,因此甲班学生成绩的众数,
将乙班名学生的成绩从小到大排列,处在中间位置的两个数的平均数为,因此中位数,
故答案为:,;
(3)(人),
答:甲班、乙班共人为样本估计全年级人中优秀人数约为人.
【点睛】本题考查中位数、众数,频数分布表,掌握中位数、众数以及“频率”是正确解答的前提.
22.(1)
(2)
【分析】(1)直接由概率公式求解即可;
(2)画树状图,共有12种等可能的结果,其中两个转盘的指针指向的数字都是3的结果有2种,再由概率公式求解即可.
【详解】(1)解:转动一次A盘,指针指向3的概率是,
故答案为:;
(2)画树状图如下:
共有12种等可能的结果,其中两个转盘的指针指向的数字都是3的结果有2种,
∴两个转盘的指针指向的数字都是3的概率为:.
【点睛】本题考查树状图法求概率,树状图法可以不重不漏的列举出所有可能发生的情况,适合于两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.
23.(1)见解析
(2)见解析
【分析】(1)先证明,由全等三角形的性质可得,然后根据可得,最后根据等量代换即可证明结论;
(2)直接运用全等三角形对应角相等的性质即可证明结论.
【详解】(1)证明:∵,
∴,即,
在和中,
,
∴,
∴,
又∵,
∴,
∴.
(2)证明:∵,
∴.
【点睛】本题主要考查了全等三角形的判定与性质,证得是解答本题的关键.
24.(1)每份菜品甲的利润为15元,每份菜品乙的利润为10元
(2)购进甲菜品200份,乙菜品400份,所获利润最大,最大利润为7000元
【分析】(1)设每份菜品甲的利润为元,每份菜品乙的利润为元,根据售出2份甲菜品和1份乙菜品可获利40元,售出3份甲菜品和2份乙菜品可获利65元,列二元一次方程组,求解即可;
(2)设销售甲菜品份,总利润为元,根据甲菜品的数量不多于乙菜品的一半,求出的取值范围,再表示出与的函数关系式,根据一次函数的增减性即可确定最大利润时进货方案,进一步求出最大利润即可.
【详解】(1)解:设每份菜品甲的利润为元,每份菜品乙的利润为元,
根据题意,得:,
解得:,
答:每份菜品甲的利润为15元,每份菜品乙的利润为10元;
(2)设销售甲菜品份,总利润为元,
根据题意,得:,
解得:,
,
∵,
∴随着的增大而增大,
当时,取得最大值,最大值为:(元),
此时销售乙菜品:(份),
答:销售甲菜品200份,乙菜品400份,所获利润最大,最大利润为7000元.
【点睛】本题考查一次函数的应用,二元一次方程组的应用,一元一次不等式的应用,理解题意是解题的关键.
25.(1)
(2)15.5
【分析】(1)根据题意可以求得圆心的坐标和圆的半径,从而可以求得圆形区域的面积;
(2)过点A作轴于点D,依题意,得,在中,设,则,由,根据图形得到则,解方程求得x,进而解直角三角形求得
【详解】(1)连接,则轴,
∴,
设为由O、B、C三点所确定圆的圆心,
则为的直径,
由已知得,由勾股定理得,
∴半径,
∴;
(2)过点A作轴于点D,依题意,得,
在中,设,
则,
∴,
∴,
由题意得:,
则,
解得:,
在中,有,即,
∴
【点睛】本题考查了勾股定理的应用、解直角三角形以及圆的面积计算等知识.熟练掌握圆由半径和圆心确定是解答本题的关键.
26.(1)
(2)
(3)存在,
【分析】(1)用待定系数法即可求解;
(2)由,即可求解;
(3)是平行四边形的边,且点向右平移个单位向下平移个单位得到点,则点向右平移个单位向下平移个单位得到点,进而求解.
【详解】(1)解:∵点在反比例函数图像上,
∴,
∴反比例函数的表达式为,
当时,,
∴,
∵,在一次函数图像上,
∴,
解得:,
∴一次函数的表达式为;
(2)设直线交轴于点,
当时,,解得:
∴点,
设点,
∵的面积为,
∴,
∴,
解得:,
∴点的坐标为;
(3)存在,理由:
设直线的解析式为,,,
∴,
解得:,
直线的解析式为,
设点,
∵是平行四边形的边,且点向右平移个单位向下平移个单位得到点,点在轴上,
∴点向右平移个单位向下平移个单位得到点,
∴
∴,
∴点的坐标为.
【点睛】本题是反比例函数综合题,考查了待定系数法求函数解析式,三角形面积,平行四边形性质等,解题关键是运用点坐标平移的规律:左减右加纵不变,上加下减横不变解决问题.
27.(1)
(2)①;②
【分析】(1)用待定系数法即可求解;
(2)①由直线的表达式知,其和轴负半轴的夹角为,即,则,进而求解;
②作点关于轴的对称点,则,用解直角三角形的方法求出,进而求解.
【详解】(1)解:∵抛物线经过点,,
∴,
解得:,
∴抛物线的解析式为;
(2)①∵抛物线的解析式为,
当时,,
∴,
设直线的解析式为,,,
∴,
解得:,
∴直线的解析式为,
设点,点,
∴,
∵,
∴当时,的最大值为,
∵,,
∴,
∴,
∵轴,作轴,
∴,,
∴,,
∴,
∴的最大值为;
②作点关于轴的对称点,连接、,
∴垂直平分,
∴,
∴,
∵,
∴,
过点作于点,
∴,
∴,
∴,
∴,
∴,
设直线与轴交于点,
∴,
∴,
当点在轴的正半轴时,,
设直线的解析式为,,,
∴,
解得:,
∴直线的解析式为,
∵点在抛物线上,
∴,
解得:(此时是钝角,不合题意,舍去),(舍去),
当点在轴的负半轴时,,
设直线的解析式为,,,
∴,
解得:,
∴直线的解析式为,
∵点在抛物线上,
∴,
解得:,(舍去),
综上所述,点的横坐标为.
【点睛】本题是二次函数的综合题,考查了运用待定系数法求函数的解析式,二次函数与一次函数的交点坐标,对称的性质,平行线的性质,等角对等边,三角形内角和,勾股定理,三角函数定义的应用,二次函数的最值等知识点,运用了分类讨论和等积法的思想.解题关键是正确添加辅助线构造等角和等积法的运用.
28.(1);(2);(3)①;②平方米
【分析】(1)根据矩形的判定定理得到四边形是矩形,求得,根据正方形的性质得到,,根据全等三角形的性质得到,根据勾股定理即可得到结论;
(2)如图②,延长交于,延长交于,根据全等三角形的性质得到,,求得,根据余角的性质得到,同理,,根据全等三角形的性质得到,求得正方形的面积,于是得到结论;
(3)①如图③,连接,根据勾股定理得到,根据勾股定理的逆定理得到,推出是所在圆的直径,是等腰直角三角形,得到点,,,四点共圆,,圆内接四边形的性质得到的度数;
②根据三角形的面积公式得到;根据旋转的想得到,,,延长交于,推出是等腰直角三角形,得到,根据勾股定理和三角形的面积公式即可得到结论.
【详解】解:∵,,,
∴,
∴四边形是矩形,
∴,
∴,
∵四边形是正方形,
∴,,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴,
解得:或(负值不合题意,舍去),
∴的长为;
(2)解:如图②,延长交于,延长交于,
∵四边形是正方形,
∴,
∵,,
在和中,
,
∴,
∴,,,
∵,
∴,
∴,
∴,
∴,
同理,,
在和中,
,
∴,
∴,,
在和中,
,
∴,
∴,,
∴,,
∴,
∴四边形是正方形,
∵的面积为,,
∴正方形的面积为:,
∴正方形的面积为:,
故答案为:;
(3)如图③,连接,
∵,,
∴,
∵,,
∴,
∴,
∴是所在圆的直径,是等腰直角三角形,
∴点,,,四点共圆,,
∴,
∴,
故答案为:;
②∵是等腰直角三角形,
∴,
把绕着点逆时针旋转,得到,
∴,,,
∴∠,,
∴,
∴,
延长交于,
∴,,
∴是等腰直角三角形,,
∴,,
∴,
∵,
∴四边形是正方形,
∴,
∴,
∵,
∴,
∴,
∴
,
∴(平方米).
【点睛】本题是圆的综合题,考查旋转的性质,全等三角形的判定和性质,正方形的判定和性质,等腰直角三角形的判定和性质,圆周角定理,勾股定理,勾股定理的逆定理,正确地作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
