河北省2024届中考数学一轮模拟卷(含解析)
文档属性
| 名称 | 河北省2024届中考数学一轮模拟卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 06:37:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
河北省2024届中考数学一轮模拟卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.﹣8的立方根是( )
A.2 B.﹣2 C. D.
2.如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是( )
A.20° B.30° C.70° D.80°
3.已知.若为整数且,则的值为( )
A.43 B.44 C.45 D.46
4.如图是某商场一楼与二楼之间的手扶电梯示意图.其中、分别表示一楼、二楼地面的水平线,,的长是,则乘电梯从点到点上升的高度是( )
A. B. C. D.
5.如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
6.如图,将ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A. B. C.2 D.
7.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
A. B.
C. D.
8.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x千米/小时,根据题意,得
A. B.
C. D.
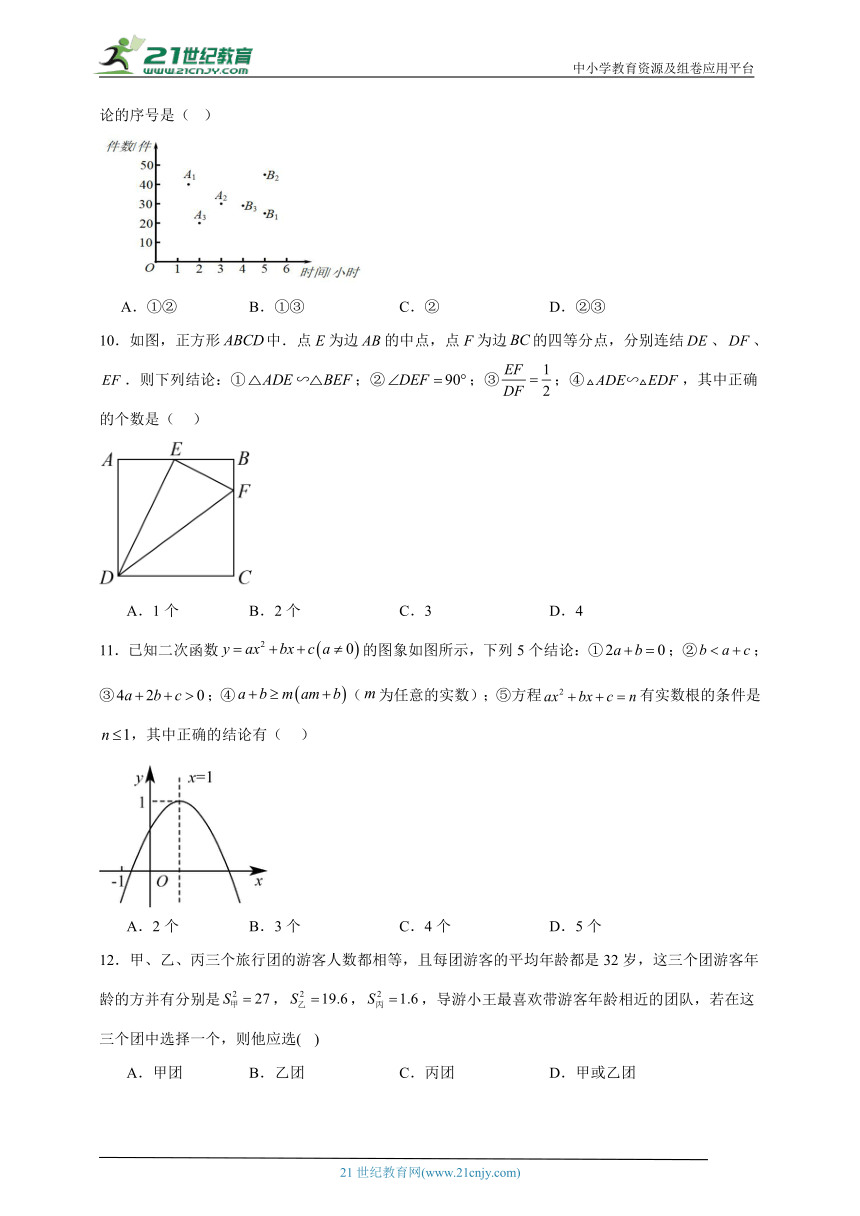
9.三名快递员某天的工作情况如图所示,其中点,,的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点,,,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.② D.②③
10.如图,正方形中.点E为边的中点,点F为边的四等分点,分别连结、、.则下列结论:①;②;③;④,其中正确的个数是( )
A.1个 B.2个 C.3 D.4
11.已知二次函数的图象如图所示,下列5个结论:①;②;③;④(为任意的实数);⑤方程有实数根的条件是,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
12.甲、乙、丙三个旅行团的游客人数都相等,且每团游客的平均年龄都是32岁,这三个团游客年龄的方并有分别是,,,导游小王最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选( )
A.甲团 B.乙团 C.丙团 D.甲或乙团
二、填空题
13.4的算术平方根是 ,的立方根是 .
14.七位女生的体重(单位:kg)分别为36、42、38、42、35、45、40,则这七位女生的体重的中位数为 kg.
15.已知 , 为一元二次方程 的两根,那么 的值为 .
16.已知点 P(m,1)与点 P′(5,n)关于点 A(﹣2,3)对称,则 m﹣n= .
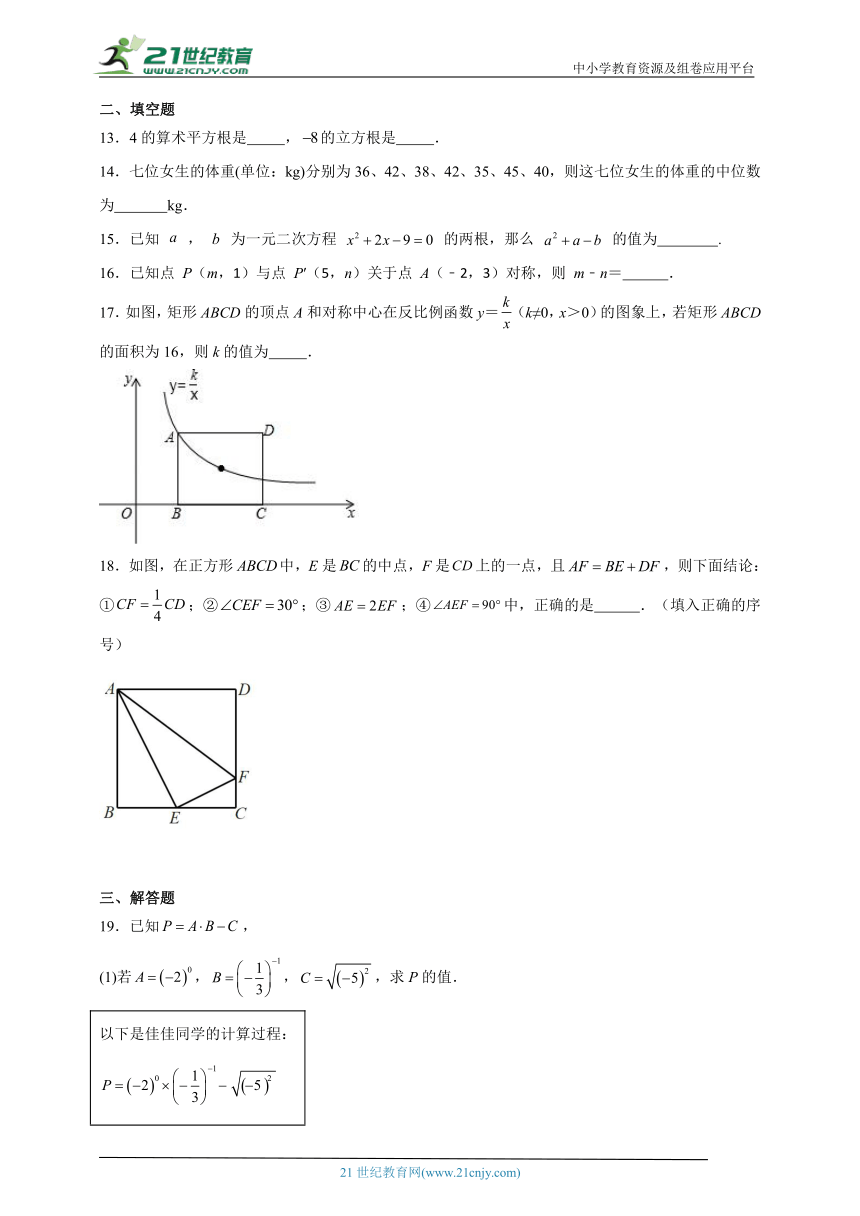
17.如图,矩形ABCD的顶点A和对称中心在反比例函数y=(k≠0,x>0)的图象上,若矩形ABCD的面积为16,则k的值为 .
18.如图,在正方形中,E是的中点,F是上的一点,且,则下面结论:①;②;③;④中,正确的是 .(填入正确的序号)
三、解答题
19.已知,
(1)若,,,求P的值.
以下是佳佳同学的计算过程: 第一步 第二步 第三步
上面的计算过程有错误吗?如果有,请你指出是第几步错误,并求出正确的P值;
(2)若,,,当x为何值时,P的值为7
20.某学校为了了解学生日常在家体育锻炼情况,从全体学生中随机抽取若干学生进行调查,以下是根据调查数据绘制的统计图表的一部分,根据信息回答下列问题:
某校学生在锻炼情况的扇形统计图: 组别 平均每日体育锻炼时间(分) 人数
A 8
B ______
C 20
D 12
(1)本次调查共______人;
(2)抽查结果中,B组有______人;
(3)在抽查得到的数据中,中位数位于______组(填组别);
(4)若该校共有学生1500人,则估计平均每日锻炼超过25分钟的学生有多少人.
21.发现:存在三个连续整数使得这三个连续整数的和等于这三个连续整数的积;
验证:连续整数,,______(填“满足”或“不满足”)这种关系;
连续整数2,3,4,______(填“满足”或“不满足”)这种关系;
延伸:设中间整数为n
(1)列式表示出三个连续整数的和、积,并分别化简;
(2)再写出一组符合“发现”要求的连续整数(直接写结果).
22.小明和小亮周末一起去公园锻炼.两人同时从公园里的甲景点出发,沿相同路线到公园里的乙景点后再以原速度立即按原路返回.小亮的步行速度是80米/分.设小明行走的时间为t分钟,如图为小明和小亮距乙景点的距离S(米)和t(分钟)之间的函数关系的部分图像.
(1)甲、乙两景点的距离为______米,小明的步行速度为______米/分;
(2)求AB段的函数解析式,并直接写出小明第一次回到甲景点时对应的坐标;
(3)在函数图像中画出小明、小亮在途中第一次相遇时的点D,并通过计算说明第一次相遇所用的时间;
(4)在小明从乙景点返回甲景点的途中,请直接写出小明和小亮之间的距离不超过100米的时长.
23.如图1,已知点A、O在直线l上,且,于O点,且,以OD为直径在OD的左侧作半圆E,于A,且.向右沿直线l平移得到,设平移距离为x.
(1)若的边经过点D,则平移的距离______;
(2)如图2,若截半圆E得到的的长为,求的度数;
(3)当的边与半圆E相切时,直接写出x的值.
24.如图,已知抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点M.
(1)若该抛物线过点
①求该抛物线的表达式,并求出此时A、B两点坐标;
②将该抛物线进行平移,平移后的抛物线对应的函数为,A点的对应点为,求点移动的最短距离;
(2)点M关于的对称轴的对称点坐标为______(用含n的代数式表示);
(3)将抛物线上的一段图像记作C,若C与直线有唯一公共点,直接写出n的取值范围______.
25.如图①,在矩形中,,,把绕点B顺时针旋转得到,连接,过B点作于E点,交矩形边于F点.(参考数据:,,)
(1)面积的最大值是______;
(2)当时,求点A运动的路径长;
(3)当点落在的垂直平分线上时,点到直线的距离是______;
(4)若,求的值.
参考答案:
1.B
【分析】根据立方根的定义求解即可.
【详解】解:∵(﹣2)3=﹣8,
∴﹣8的立方根是﹣2
故选:B.
【点睛】本题考查了立方根的定义,解题的关键是找出一个立方为-8的数,考查了学生对基础知识的理解与掌握.
2.B
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【详解】解:a,b相交所成的锐角=100° 70°=30°.
故选:B.
【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
3.B
【分析】由题意可直接进行求解.
【详解】解:∵,
∴,
∴,
∴;
故选B.
【点睛】本题主要考查算术平方根,熟练掌握算术平方根是解题的关键.
4.B
【分析】过作于,求出,根据含度的直角三角形性质求出即可.
【详解】解:过作于,
则,,
,
,
,
故选:B.
【点睛】本题考查了含度角的直角三角形性质的应用,构造直角三角形是解此题的关键所在,题目比较好,难度也不大.
5.B
【分析】先根据角平分线及平行线的性质得出∠BAE=∠AEB,再由等角对等边得出BE=AB,从而求出EC的长.
【详解】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=3,
∴EC=BC-BE=5-3=2,
故选:B.
【点睛】本题主要考查了角平分线、平行四边形的性质及等腰三角形的判定,根据已知得出∠BAE=∠AEB是解决问题的关键.
6.D
【分析】首先构造以∠A为锐角的直角三角形,然后利用正切的定义即可求解.
【详解】解:连接BD,如图所示:
根据网格特点可知,,
∴,
∵, ,
∴在Rt△ABD中,tanA==,故D正确.
故选:D.
【点睛】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,构造直角三角形是本题的关键.
7.C
【详解】解:第一个阶段,逆水航行,用时较多;第二个阶段,在乙地停留一段时间,随着时间的增长,路程不再变化,函数图象将与x轴平行;第三个阶段,顺水航行,所走的路程继续增加,相对于第一个阶段,用时较少,
故选C.
8.A
【分析】若设走路线一时的平均速度为x千米/小时,根据路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达可列出方程.
【详解】解:设走路线一时的平均速度为x千米/小时,
故选A.
9.B
【分析】根据所给的点的信息进行辨析即可得解.
【详解】①上午派送快递所用时间最短的是A1,即甲,不足2小时;故①正确;
②下午派送快递件数最多的是B2即乙,超过40件,其余的不超过40件,故②错误;
③在这一天中派送快递总件数为:甲:40+25=65(件),乙:45+30=75;丙:30+20=50,所以这一天中派送快递总件数最多的是乙,故③正确.
故选B.
【点睛】本题考查的知识点是函数的图象,分析出图象中点的几何意义,是解答的关键.
10.C
【分析】设正方形的边长为4,根据两边对应成比例且夹角相等的两个三角形相似可判断①和④;根据相似三角形的性质可判断②;根据勾股定理可判断③.
【详解】设正方形的边长为4,
∵点E为边的中点,点F为边的四等分点,
∴,.
①∵,,
∴,
∵,
∴,故①正确;
②∵,
∴,
∵,
∴,
∴,故②正确;
③∵,,
∴,故③不正确;
④,,
∴
∵,
∴,故④正确.
故选C.
【点睛】本题考查了正方形的性质,勾股定理,相似三角形的判定与性质,熟练掌握各知识点是解答本题的关键.
11.C
【分析】根据二次函数的图像与性质逐项判断即可.
【详解】解:由图象可知,抛物线对称轴为直线,
,
,
故①正确;
当时,,
,
,
故②错误;
由抛物线的对称性可知,当时,,
,
故③正确;
当时,有最大值,此时,
当时,,
,
,即(为任意的实数).
故④正确;
由图象可知,时,函数图象上找不到与之对应的值,
方程有实数根的条件是,
故⑤正确;
综上所述,正确的有①③④⑤,共4个,
故选:C.
【点睛】此题主要考查了二次函数图象与二次函数系数之间的关系,二次函数与一元二次方程的联系,二次函数的图像与性质,解题的关键是熟练掌握二次函数的图像和系数的关系.
12.C
【分析】方差越大则数据的离中程度就越大,故方差越小离中程度就越小,数据越稳定.
【详解】解:方差越大则数据的离中程度就越大,故方差越小离中程度就越小,数据越稳定.
故选:C.
【点睛】本题考查的统计相关知识.
13. 2
【分析】根据算术平方根和立方根的定义求出即可.
【详解】解:4的算术平方根是,的立方根是,
故答案为:2;.
【点睛】本题主要考查了求一个数的算术平方根和立方根,解题的关键是熟练掌握算术平方根和立方根定义,准确计算.
14.40
【详解】题目中数据共有7个,中位数是按从小到大排列后第4个数作为中位数,故这组数据的中位数是40.
15.11
【分析】根据a与b为方程的两根,把x=a代入方程,并利用根与系数的关系求出所求即可.
【详解】解:∵ , 为一元二次方程 的两根
∴a+b=-2, ,即
∴ .
故答案为:11.
【点睛】本题考查了根与系数的关系,熟练掌握根与系数的关系是解本题的关键.
16.-14
【分析】由点P(m,1)与点P′(5,n)关于点A(-2,3)对称,可得点A是线段PP′的中点,根据中点坐标公式求出m、n的值,再代入m-n计算即可.
【详解】解:∵点P(m,1)与点P′(5,n)关于点A(-2,3)对称,
∴=-2,=3,
∴m=-9,n=5,
则m-n=-9-5=-14.
故答案为-14.
【点睛】本题考查了坐标与图形变化-旋转,得出m、n的值是解题关键.
17.8
【分析】设A点的坐标为(m,n)则根据矩形的性质得出矩形中心的纵坐标为,根据中心在反比例函数y=上,求出中心的横坐标为,进而可得出BC的长度,根据矩形ABCD的面积即可求得.
【详解】解:如图,延长DA交y轴于点E,
∵四边形ABCD是矩形,
设A点的坐标为(m,n)则根据矩形的性质得出矩形中心的纵坐标为,
∵矩形ABCD的中心都在反比例函数y=上,
∴x=,
∴矩形ABCD中心的坐标为(,)
∴BC=2(﹣m)=﹣2m,
∵S矩形ABCD=16,
∴(﹣2m) n=16.
4k﹣2mn=16,
∵点A(m,n)在y=上,
∴mn=k,
∴4k﹣2k=16,
解得:k=8
故答案为8.
【点睛】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中k=xy为定值是解答此题的关键.
18.①③④
【分析】设正方形的边长为2,为x,则,由E是的中点及,可用含x的式子表示出,然后分别利用勾股定理和含角的直角三角形的性质对各个结论进行分析判断即可.
【详解】解:设正方形的边长为2,为x,则,
是的中点,
.
,
.
在中,,
,
,
,
,正确;
在中,,,
,错误;
在中,,,
,同理可得,
,正确;
在中,,,
.
,
,正确.
综上,正确的有.
故答案为:.
【点睛】本题考查了正方形的性质、勾股定理及其逆定理和含角的直角三角形的性质等知识点,熟练掌握相关性质及定理是解题的关键.
19.(1)第一步,
(2)
【分析】(1)根据零指数幂,负整数指数幂,开平方,按照计算法则计算即可解答;
(2)列方程,解出即可解答.
【详解】(1)解:第一步,
;
(2)解:当,,时,
,
解得:.
【点睛】本题考查了零指数幂,负整数指数幂,开平方,解一元一次方程,熟知计算法则是解题的关键.
20.(1)
(2)
(3)C
(4)800人
【分析】(1)利用D组的人数除以对应的百分比即可求得答案;
(2)用总人数减去A、C、D三个组的人数即可得到B组的人数;
(3)根据中位数的求法即可判断中位数所在小组;
(4)用全校总人数乘以被调查人数中平均每日锻炼超过25分钟的学生的占比,即可得到答案.
【详解】(1)解:(人),即本次调查共人,
故答案为:.
(2)抽查结果中,B组有(人),
故答案为:.
(3)60个数据按照从小到大排列后,处在中间的两个数位于C组,
∴在抽查得到的数据中,中位数位于C组,
故答案为:C.
(4)(人),
答:平均每日锻炼超过25分钟的学生有800人.
【点睛】此题考查了扇形统计图和统计表,读懂题意计算正确是解题的关键.
21.验证:满足;不满足;(1)和为,积为;(2),0,1(答案不唯一)
【分析】先分别计算和的值,比较两组值是否相等;再分别计算和的值,比较两组值是否相等即可;
(1)设中间整数为,则三个连续整数可表示为:,,,将,,三数相加得其和;将,,三数相乘得其积;
(2)令(1)中的和等于积,解方程,求得的值,从而可得符合要求的连续整数.
【详解】验证:解:,
,,满足这种关系;
,,,
,
2,3,4不满足这种关系.
延伸:设中间整数为,则三个连续整数可表示为:,,,
(1)三个连续整数的和可表示为:,
三个连续整数的积可表示为:,
(2)当时,
解得:,或,
符合要求的一组连续整数为:,0,1.
【点睛】本题考查了探究某类数的规律性问题,其中涉及到了因式分解方法的运用,按照要求写出相关数或式子,按照规则计算,是解答本题的关键.
22.(1)560;70
(2),
(3)见解析,分钟
(4)分钟
【分析】(1)由小亮的速度为80,结合图像知道其时间,即可得解;
(2)设段函数表达式为,代入A,B点坐标即可;结合(1)即可知小明第一次回到甲景点时对应的坐标;
(3)画出函数图像,联立的函数解析式求解,即可得小明和小亮第一次相遇所用的时间;
(4)在小明从乙景点返回甲景点的途中,与小亮的距离恰好是100米列方程计算即可.
【详解】(1)由图可知,小亮到达乙地时间为7小时,故(米),故小明的速度为(米/分)
560;70
(2)由(1)得,,设段函数表达式为,把,
代入得:,解得:
∴段函数解析式为,
由题图可知小明到乙景点所用时间为8分钟,匀速步行,甲乙两地距离为560米,
∴小明第一次回到甲景点时对应的坐标为;
(3)画出函数图像如图.
由,得AC的函数解析式为,
由,得BE的函数解析式为,
联立方程组得解得:.
∴小明和小亮第一次相遇所用的时间为分钟.
(4)设经过分钟,小明与小亮的距离恰好是100米,依题意:
,
解得:
当小亮到达甲地,小明继续返回,距离甲地恰好100米,距离又开始缩小,时间为,故总时间为 (分钟),
故答案为:分钟
【点睛】本题主要考查一次函数的应用,分析题意,理解图像上点的坐标,正确的得出一次函数的解析式是解题的关键.
23.(1)
(2)
(3)或
【分析】(1)由平移性质和正切函数求解即可;
(2)在图2中,连接、、,由弧长公式求得,进而得到是等边三角形,证得,则,根据等腰三角形的性质和三角形的内角和定理求解即可;
(3)根据题意,分当的边与半圆E相切和的边与半圆E相切两种情况,分别画出图形,利用切线性质和锐角三角函数求解即可.
【详解】(1)解:如图1,
由平移性质得,
∵,,
∴,
∴平移距离,
故答案为:;
(2)解:连接、、,如图2所示,
则半圆E的半径,
设,
∵截半圆E的的长为,
∴,
解得:,
∴,
∵,
∴是等边三角形,
∴.
∴,
∵,
∴,
∵,
∴;
(3)解:根据题意,分两种情况:
当的边与半圆E相切时,如图3,
设切点为P,连接,则,
∵,,
∴,
∴,
∴平移的距离;
当的边与半圆E相切时,如图4,
设切点为P,连接并延长交l于N,则,
∵,,
∴,又,
∴,,
∴,
∵,,
∴,
∴,
∴平移的距离,
综上,平移的距离x的值为或.
【点睛】本题考查平移性质、切线性质、解直角三角形、弧长公式、角平分线的性质、三角形和四边形的内角和、等边三角形的判定与性质、等腰三角形的性质等知识,熟练掌握相关知识的联系与运用,利用数形结合和分类讨论思想求解是解答的关键.
24.(1)①,;;②两个单位
(2)
(3)或
【分析】(1)①将已知点坐标代入解析式,确定待定参数值;根据具体解析式,转化为方程,确定与坐标轴交点坐标;比较平移前后的解析式求解;
(2)根据抛物线的对称性解答;
(3)随着参数n的变化,抛物线形状不变,顶点在直线上移动,将抛物线由下向上平移,找出临界状态,进而结合一元二次方程判别式、图像端点之间的位置关系求解.
【详解】(1)①将代入,得
解得:,所以
令,则
解得:,
∴
②将向上平移2个单位可以得到
所以A点向上平移最短距离是两个单位得;
(2),故点,
抛物线的对称轴为,所以点M的横坐标为,所以点M关于对称轴的对称点坐标为.
(3)如图,,顶点在直线上,点关于对称轴的对称点在直线上,
当抛物线整体与直线有唯一交点时,联立解析式,,即,
∴,解得,,满足题意;
直线与直线的交点为,与y轴的交点,
抛物线向上移动,当点M在直线上方且点N在直线下方或在直线上时,C与直线有且只有一个交点,
∴
综上,或
【点睛】本题考查二次函数解析式,抛物线的图像及性质,函数图像的交点问题;根据含参解析式确定函数图像特征及位置的动态变化是解题的关键.
25.(1)18
(2)
(3)
(4)或
【分析】(1)当落在边上时,面积最大,此时是等腰直角三角形,即可求解;
(2)先求出,即可求出,用弧长公式求解即可;
(3)根据题意画出图形,用勾股定理求出即可求解;
(4)分两种情况讨论:当点F在上;点F在上.
【详解】(1)解:如图所示,的运动轨迹,过点作,
由图可知,当落在边上时,最长,即面积最大,此时,
∵,
由旋转性质可得:,
∴此时是等腰直角三角形,
∴;
(2)解:当时,点F在边上,
∵是矩形,
∴
∴ ,
∴,
∴,
∴点A运动的路径长是:;
(3)解:点落在的垂直平分线上,如图所示,
∵,
由旋转性质可得:,
∵点落在的垂直平分线上,
∴,
∴,
∵,
∴,
∴
即点到直线的距离是;
(4)解:①当点F在上时,如图所示,
,
∵,,,
∴,
由旋转性质可得:,
∵四边形是矩形,
∴四边形是正方形,
过E作于H点,
∴,,
∴;
②当点F在上时,
∵,,,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴,
过E作于H点,
∴,
∴,
∴,即,
∴,,
∴,
∴;
∴的值为或.
【点睛】本题考查了旋转几何问题,涉及到相似三角形的判定与性质、作辅助线、勾股定理等,熟练掌握知识点是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
河北省2024届中考数学一轮模拟卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.﹣8的立方根是( )
A.2 B.﹣2 C. D.
2.如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是( )
A.20° B.30° C.70° D.80°
3.已知.若为整数且,则的值为( )
A.43 B.44 C.45 D.46
4.如图是某商场一楼与二楼之间的手扶电梯示意图.其中、分别表示一楼、二楼地面的水平线,,的长是,则乘电梯从点到点上升的高度是( )
A. B. C. D.
5.如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A.2和3 B.3和2 C.4和1 D.1和4
6.如图,将ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A. B. C.2 D.
7.一艘轮船在同一航线上往返于甲、乙两地.已知轮船在静水中的速度为15 km/h,水流速度为5 km/h.轮船先从甲地顺水航行到乙地,在乙地停留一段时间后,又从乙地逆水航行返回到甲地.设轮船从甲地出发后所用时间为t(h),航行的路程为s(km),则s与t的函数图象大致是( )
A. B.
C. D.
8.小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x千米/小时,根据题意,得
A. B.
C. D.
9.三名快递员某天的工作情况如图所示,其中点,,的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点,,,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
A.①② B.①③ C.② D.②③
10.如图,正方形中.点E为边的中点,点F为边的四等分点,分别连结、、.则下列结论:①;②;③;④,其中正确的个数是( )
A.1个 B.2个 C.3 D.4
11.已知二次函数的图象如图所示,下列5个结论:①;②;③;④(为任意的实数);⑤方程有实数根的条件是,其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
12.甲、乙、丙三个旅行团的游客人数都相等,且每团游客的平均年龄都是32岁,这三个团游客年龄的方并有分别是,,,导游小王最喜欢带游客年龄相近的团队,若在这三个团中选择一个,则他应选( )
A.甲团 B.乙团 C.丙团 D.甲或乙团
二、填空题
13.4的算术平方根是 ,的立方根是 .
14.七位女生的体重(单位:kg)分别为36、42、38、42、35、45、40,则这七位女生的体重的中位数为 kg.
15.已知 , 为一元二次方程 的两根,那么 的值为 .
16.已知点 P(m,1)与点 P′(5,n)关于点 A(﹣2,3)对称,则 m﹣n= .
17.如图,矩形ABCD的顶点A和对称中心在反比例函数y=(k≠0,x>0)的图象上,若矩形ABCD的面积为16,则k的值为 .
18.如图,在正方形中,E是的中点,F是上的一点,且,则下面结论:①;②;③;④中,正确的是 .(填入正确的序号)
三、解答题
19.已知,
(1)若,,,求P的值.
以下是佳佳同学的计算过程: 第一步 第二步 第三步
上面的计算过程有错误吗?如果有,请你指出是第几步错误,并求出正确的P值;
(2)若,,,当x为何值时,P的值为7
20.某学校为了了解学生日常在家体育锻炼情况,从全体学生中随机抽取若干学生进行调查,以下是根据调查数据绘制的统计图表的一部分,根据信息回答下列问题:
某校学生在锻炼情况的扇形统计图: 组别 平均每日体育锻炼时间(分) 人数
A 8
B ______
C 20
D 12
(1)本次调查共______人;
(2)抽查结果中,B组有______人;
(3)在抽查得到的数据中,中位数位于______组(填组别);
(4)若该校共有学生1500人,则估计平均每日锻炼超过25分钟的学生有多少人.
21.发现:存在三个连续整数使得这三个连续整数的和等于这三个连续整数的积;
验证:连续整数,,______(填“满足”或“不满足”)这种关系;
连续整数2,3,4,______(填“满足”或“不满足”)这种关系;
延伸:设中间整数为n
(1)列式表示出三个连续整数的和、积,并分别化简;
(2)再写出一组符合“发现”要求的连续整数(直接写结果).
22.小明和小亮周末一起去公园锻炼.两人同时从公园里的甲景点出发,沿相同路线到公园里的乙景点后再以原速度立即按原路返回.小亮的步行速度是80米/分.设小明行走的时间为t分钟,如图为小明和小亮距乙景点的距离S(米)和t(分钟)之间的函数关系的部分图像.
(1)甲、乙两景点的距离为______米,小明的步行速度为______米/分;
(2)求AB段的函数解析式,并直接写出小明第一次回到甲景点时对应的坐标;
(3)在函数图像中画出小明、小亮在途中第一次相遇时的点D,并通过计算说明第一次相遇所用的时间;
(4)在小明从乙景点返回甲景点的途中,请直接写出小明和小亮之间的距离不超过100米的时长.
23.如图1,已知点A、O在直线l上,且,于O点,且,以OD为直径在OD的左侧作半圆E,于A,且.向右沿直线l平移得到,设平移距离为x.
(1)若的边经过点D,则平移的距离______;
(2)如图2,若截半圆E得到的的长为,求的度数;
(3)当的边与半圆E相切时,直接写出x的值.
24.如图,已知抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点M.
(1)若该抛物线过点
①求该抛物线的表达式,并求出此时A、B两点坐标;
②将该抛物线进行平移,平移后的抛物线对应的函数为,A点的对应点为,求点移动的最短距离;
(2)点M关于的对称轴的对称点坐标为______(用含n的代数式表示);
(3)将抛物线上的一段图像记作C,若C与直线有唯一公共点,直接写出n的取值范围______.
25.如图①,在矩形中,,,把绕点B顺时针旋转得到,连接,过B点作于E点,交矩形边于F点.(参考数据:,,)
(1)面积的最大值是______;
(2)当时,求点A运动的路径长;
(3)当点落在的垂直平分线上时,点到直线的距离是______;
(4)若,求的值.
参考答案:
1.B
【分析】根据立方根的定义求解即可.
【详解】解:∵(﹣2)3=﹣8,
∴﹣8的立方根是﹣2
故选:B.
【点睛】本题考查了立方根的定义,解题的关键是找出一个立方为-8的数,考查了学生对基础知识的理解与掌握.
2.B
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
【详解】解:a,b相交所成的锐角=100° 70°=30°.
故选:B.
【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.
3.B
【分析】由题意可直接进行求解.
【详解】解:∵,
∴,
∴,
∴;
故选B.
【点睛】本题主要考查算术平方根,熟练掌握算术平方根是解题的关键.
4.B
【分析】过作于,求出,根据含度的直角三角形性质求出即可.
【详解】解:过作于,
则,,
,
,
,
故选:B.
【点睛】本题考查了含度角的直角三角形性质的应用,构造直角三角形是解此题的关键所在,题目比较好,难度也不大.
5.B
【分析】先根据角平分线及平行线的性质得出∠BAE=∠AEB,再由等角对等边得出BE=AB,从而求出EC的长.
【详解】解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴BE=AB=3,
∴EC=BC-BE=5-3=2,
故选:B.
【点睛】本题主要考查了角平分线、平行四边形的性质及等腰三角形的判定,根据已知得出∠BAE=∠AEB是解决问题的关键.
6.D
【分析】首先构造以∠A为锐角的直角三角形,然后利用正切的定义即可求解.
【详解】解:连接BD,如图所示:
根据网格特点可知,,
∴,
∵, ,
∴在Rt△ABD中,tanA==,故D正确.
故选:D.
【点睛】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边,构造直角三角形是本题的关键.
7.C
【详解】解:第一个阶段,逆水航行,用时较多;第二个阶段,在乙地停留一段时间,随着时间的增长,路程不再变化,函数图象将与x轴平行;第三个阶段,顺水航行,所走的路程继续增加,相对于第一个阶段,用时较少,
故选C.
8.A
【分析】若设走路线一时的平均速度为x千米/小时,根据路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达可列出方程.
【详解】解:设走路线一时的平均速度为x千米/小时,
故选A.
9.B
【分析】根据所给的点的信息进行辨析即可得解.
【详解】①上午派送快递所用时间最短的是A1,即甲,不足2小时;故①正确;
②下午派送快递件数最多的是B2即乙,超过40件,其余的不超过40件,故②错误;
③在这一天中派送快递总件数为:甲:40+25=65(件),乙:45+30=75;丙:30+20=50,所以这一天中派送快递总件数最多的是乙,故③正确.
故选B.
【点睛】本题考查的知识点是函数的图象,分析出图象中点的几何意义,是解答的关键.
10.C
【分析】设正方形的边长为4,根据两边对应成比例且夹角相等的两个三角形相似可判断①和④;根据相似三角形的性质可判断②;根据勾股定理可判断③.
【详解】设正方形的边长为4,
∵点E为边的中点,点F为边的四等分点,
∴,.
①∵,,
∴,
∵,
∴,故①正确;
②∵,
∴,
∵,
∴,
∴,故②正确;
③∵,,
∴,故③不正确;
④,,
∴
∵,
∴,故④正确.
故选C.
【点睛】本题考查了正方形的性质,勾股定理,相似三角形的判定与性质,熟练掌握各知识点是解答本题的关键.
11.C
【分析】根据二次函数的图像与性质逐项判断即可.
【详解】解:由图象可知,抛物线对称轴为直线,
,
,
故①正确;
当时,,
,
,
故②错误;
由抛物线的对称性可知,当时,,
,
故③正确;
当时,有最大值,此时,
当时,,
,
,即(为任意的实数).
故④正确;
由图象可知,时,函数图象上找不到与之对应的值,
方程有实数根的条件是,
故⑤正确;
综上所述,正确的有①③④⑤,共4个,
故选:C.
【点睛】此题主要考查了二次函数图象与二次函数系数之间的关系,二次函数与一元二次方程的联系,二次函数的图像与性质,解题的关键是熟练掌握二次函数的图像和系数的关系.
12.C
【分析】方差越大则数据的离中程度就越大,故方差越小离中程度就越小,数据越稳定.
【详解】解:方差越大则数据的离中程度就越大,故方差越小离中程度就越小,数据越稳定.
故选:C.
【点睛】本题考查的统计相关知识.
13. 2
【分析】根据算术平方根和立方根的定义求出即可.
【详解】解:4的算术平方根是,的立方根是,
故答案为:2;.
【点睛】本题主要考查了求一个数的算术平方根和立方根,解题的关键是熟练掌握算术平方根和立方根定义,准确计算.
14.40
【详解】题目中数据共有7个,中位数是按从小到大排列后第4个数作为中位数,故这组数据的中位数是40.
15.11
【分析】根据a与b为方程的两根,把x=a代入方程,并利用根与系数的关系求出所求即可.
【详解】解:∵ , 为一元二次方程 的两根
∴a+b=-2, ,即
∴ .
故答案为:11.
【点睛】本题考查了根与系数的关系,熟练掌握根与系数的关系是解本题的关键.
16.-14
【分析】由点P(m,1)与点P′(5,n)关于点A(-2,3)对称,可得点A是线段PP′的中点,根据中点坐标公式求出m、n的值,再代入m-n计算即可.
【详解】解:∵点P(m,1)与点P′(5,n)关于点A(-2,3)对称,
∴=-2,=3,
∴m=-9,n=5,
则m-n=-9-5=-14.
故答案为-14.
【点睛】本题考查了坐标与图形变化-旋转,得出m、n的值是解题关键.
17.8
【分析】设A点的坐标为(m,n)则根据矩形的性质得出矩形中心的纵坐标为,根据中心在反比例函数y=上,求出中心的横坐标为,进而可得出BC的长度,根据矩形ABCD的面积即可求得.
【详解】解:如图,延长DA交y轴于点E,
∵四边形ABCD是矩形,
设A点的坐标为(m,n)则根据矩形的性质得出矩形中心的纵坐标为,
∵矩形ABCD的中心都在反比例函数y=上,
∴x=,
∴矩形ABCD中心的坐标为(,)
∴BC=2(﹣m)=﹣2m,
∵S矩形ABCD=16,
∴(﹣2m) n=16.
4k﹣2mn=16,
∵点A(m,n)在y=上,
∴mn=k,
∴4k﹣2k=16,
解得:k=8
故答案为8.
【点睛】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中k=xy为定值是解答此题的关键.
18.①③④
【分析】设正方形的边长为2,为x,则,由E是的中点及,可用含x的式子表示出,然后分别利用勾股定理和含角的直角三角形的性质对各个结论进行分析判断即可.
【详解】解:设正方形的边长为2,为x,则,
是的中点,
.
,
.
在中,,
,
,
,
,正确;
在中,,,
,错误;
在中,,,
,同理可得,
,正确;
在中,,,
.
,
,正确.
综上,正确的有.
故答案为:.
【点睛】本题考查了正方形的性质、勾股定理及其逆定理和含角的直角三角形的性质等知识点,熟练掌握相关性质及定理是解题的关键.
19.(1)第一步,
(2)
【分析】(1)根据零指数幂,负整数指数幂,开平方,按照计算法则计算即可解答;
(2)列方程,解出即可解答.
【详解】(1)解:第一步,
;
(2)解:当,,时,
,
解得:.
【点睛】本题考查了零指数幂,负整数指数幂,开平方,解一元一次方程,熟知计算法则是解题的关键.
20.(1)
(2)
(3)C
(4)800人
【分析】(1)利用D组的人数除以对应的百分比即可求得答案;
(2)用总人数减去A、C、D三个组的人数即可得到B组的人数;
(3)根据中位数的求法即可判断中位数所在小组;
(4)用全校总人数乘以被调查人数中平均每日锻炼超过25分钟的学生的占比,即可得到答案.
【详解】(1)解:(人),即本次调查共人,
故答案为:.
(2)抽查结果中,B组有(人),
故答案为:.
(3)60个数据按照从小到大排列后,处在中间的两个数位于C组,
∴在抽查得到的数据中,中位数位于C组,
故答案为:C.
(4)(人),
答:平均每日锻炼超过25分钟的学生有800人.
【点睛】此题考查了扇形统计图和统计表,读懂题意计算正确是解题的关键.
21.验证:满足;不满足;(1)和为,积为;(2),0,1(答案不唯一)
【分析】先分别计算和的值,比较两组值是否相等;再分别计算和的值,比较两组值是否相等即可;
(1)设中间整数为,则三个连续整数可表示为:,,,将,,三数相加得其和;将,,三数相乘得其积;
(2)令(1)中的和等于积,解方程,求得的值,从而可得符合要求的连续整数.
【详解】验证:解:,
,,满足这种关系;
,,,
,
2,3,4不满足这种关系.
延伸:设中间整数为,则三个连续整数可表示为:,,,
(1)三个连续整数的和可表示为:,
三个连续整数的积可表示为:,
(2)当时,
解得:,或,
符合要求的一组连续整数为:,0,1.
【点睛】本题考查了探究某类数的规律性问题,其中涉及到了因式分解方法的运用,按照要求写出相关数或式子,按照规则计算,是解答本题的关键.
22.(1)560;70
(2),
(3)见解析,分钟
(4)分钟
【分析】(1)由小亮的速度为80,结合图像知道其时间,即可得解;
(2)设段函数表达式为,代入A,B点坐标即可;结合(1)即可知小明第一次回到甲景点时对应的坐标;
(3)画出函数图像,联立的函数解析式求解,即可得小明和小亮第一次相遇所用的时间;
(4)在小明从乙景点返回甲景点的途中,与小亮的距离恰好是100米列方程计算即可.
【详解】(1)由图可知,小亮到达乙地时间为7小时,故(米),故小明的速度为(米/分)
560;70
(2)由(1)得,,设段函数表达式为,把,
代入得:,解得:
∴段函数解析式为,
由题图可知小明到乙景点所用时间为8分钟,匀速步行,甲乙两地距离为560米,
∴小明第一次回到甲景点时对应的坐标为;
(3)画出函数图像如图.
由,得AC的函数解析式为,
由,得BE的函数解析式为,
联立方程组得解得:.
∴小明和小亮第一次相遇所用的时间为分钟.
(4)设经过分钟,小明与小亮的距离恰好是100米,依题意:
,
解得:
当小亮到达甲地,小明继续返回,距离甲地恰好100米,距离又开始缩小,时间为,故总时间为 (分钟),
故答案为:分钟
【点睛】本题主要考查一次函数的应用,分析题意,理解图像上点的坐标,正确的得出一次函数的解析式是解题的关键.
23.(1)
(2)
(3)或
【分析】(1)由平移性质和正切函数求解即可;
(2)在图2中,连接、、,由弧长公式求得,进而得到是等边三角形,证得,则,根据等腰三角形的性质和三角形的内角和定理求解即可;
(3)根据题意,分当的边与半圆E相切和的边与半圆E相切两种情况,分别画出图形,利用切线性质和锐角三角函数求解即可.
【详解】(1)解:如图1,
由平移性质得,
∵,,
∴,
∴平移距离,
故答案为:;
(2)解:连接、、,如图2所示,
则半圆E的半径,
设,
∵截半圆E的的长为,
∴,
解得:,
∴,
∵,
∴是等边三角形,
∴.
∴,
∵,
∴,
∵,
∴;
(3)解:根据题意,分两种情况:
当的边与半圆E相切时,如图3,
设切点为P,连接,则,
∵,,
∴,
∴,
∴平移的距离;
当的边与半圆E相切时,如图4,
设切点为P,连接并延长交l于N,则,
∵,,
∴,又,
∴,,
∴,
∵,,
∴,
∴,
∴平移的距离,
综上,平移的距离x的值为或.
【点睛】本题考查平移性质、切线性质、解直角三角形、弧长公式、角平分线的性质、三角形和四边形的内角和、等边三角形的判定与性质、等腰三角形的性质等知识,熟练掌握相关知识的联系与运用,利用数形结合和分类讨论思想求解是解答的关键.
24.(1)①,;;②两个单位
(2)
(3)或
【分析】(1)①将已知点坐标代入解析式,确定待定参数值;根据具体解析式,转化为方程,确定与坐标轴交点坐标;比较平移前后的解析式求解;
(2)根据抛物线的对称性解答;
(3)随着参数n的变化,抛物线形状不变,顶点在直线上移动,将抛物线由下向上平移,找出临界状态,进而结合一元二次方程判别式、图像端点之间的位置关系求解.
【详解】(1)①将代入,得
解得:,所以
令,则
解得:,
∴
②将向上平移2个单位可以得到
所以A点向上平移最短距离是两个单位得;
(2),故点,
抛物线的对称轴为,所以点M的横坐标为,所以点M关于对称轴的对称点坐标为.
(3)如图,,顶点在直线上,点关于对称轴的对称点在直线上,
当抛物线整体与直线有唯一交点时,联立解析式,,即,
∴,解得,,满足题意;
直线与直线的交点为,与y轴的交点,
抛物线向上移动,当点M在直线上方且点N在直线下方或在直线上时,C与直线有且只有一个交点,
∴
综上,或
【点睛】本题考查二次函数解析式,抛物线的图像及性质,函数图像的交点问题;根据含参解析式确定函数图像特征及位置的动态变化是解题的关键.
25.(1)18
(2)
(3)
(4)或
【分析】(1)当落在边上时,面积最大,此时是等腰直角三角形,即可求解;
(2)先求出,即可求出,用弧长公式求解即可;
(3)根据题意画出图形,用勾股定理求出即可求解;
(4)分两种情况讨论:当点F在上;点F在上.
【详解】(1)解:如图所示,的运动轨迹,过点作,
由图可知,当落在边上时,最长,即面积最大,此时,
∵,
由旋转性质可得:,
∴此时是等腰直角三角形,
∴;
(2)解:当时,点F在边上,
∵是矩形,
∴
∴ ,
∴,
∴,
∴点A运动的路径长是:;
(3)解:点落在的垂直平分线上,如图所示,
∵,
由旋转性质可得:,
∵点落在的垂直平分线上,
∴,
∴,
∵,
∴,
∴
即点到直线的距离是;
(4)解:①当点F在上时,如图所示,
,
∵,,,
∴,
由旋转性质可得:,
∵四边形是矩形,
∴四边形是正方形,
过E作于H点,
∴,,
∴;
②当点F在上时,
∵,,,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,即,
∴,
过E作于H点,
∴,
∴,
∴,即,
∴,,
∴,
∴;
∴的值为或.
【点睛】本题考查了旋转几何问题,涉及到相似三角形的判定与性质、作辅助线、勾股定理等,熟练掌握知识点是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
