重庆市2024届中考数学一轮模拟卷(含解析)
文档属性
| 名称 | 重庆市2024届中考数学一轮模拟卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 06:34:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
重庆市2024届中考数学一轮模拟卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.实数﹣2023的绝对值是( )
A.2023 B.﹣2023 C. D.
2.近年来出生人口持续走低,即使国家开放三孩,也缓解不了颓势,2022年我国出生人口是1062万人,数据1062万用科学记数法表示应为( )
A. B. C. D.
3.不等式组的解集是( )
A.x>﹣3 B.x<﹣3 C.x>2 D.x<2
4.若点(m,n)在函数y=2x+1的图象上,则2m﹣n的值是( )
A.2 B.﹣2 C.1 D.﹣1
5.关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A.k≤﹣4 B.k<﹣4 C.k≤4 D.k<4
6.我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )
A. B. C. D.
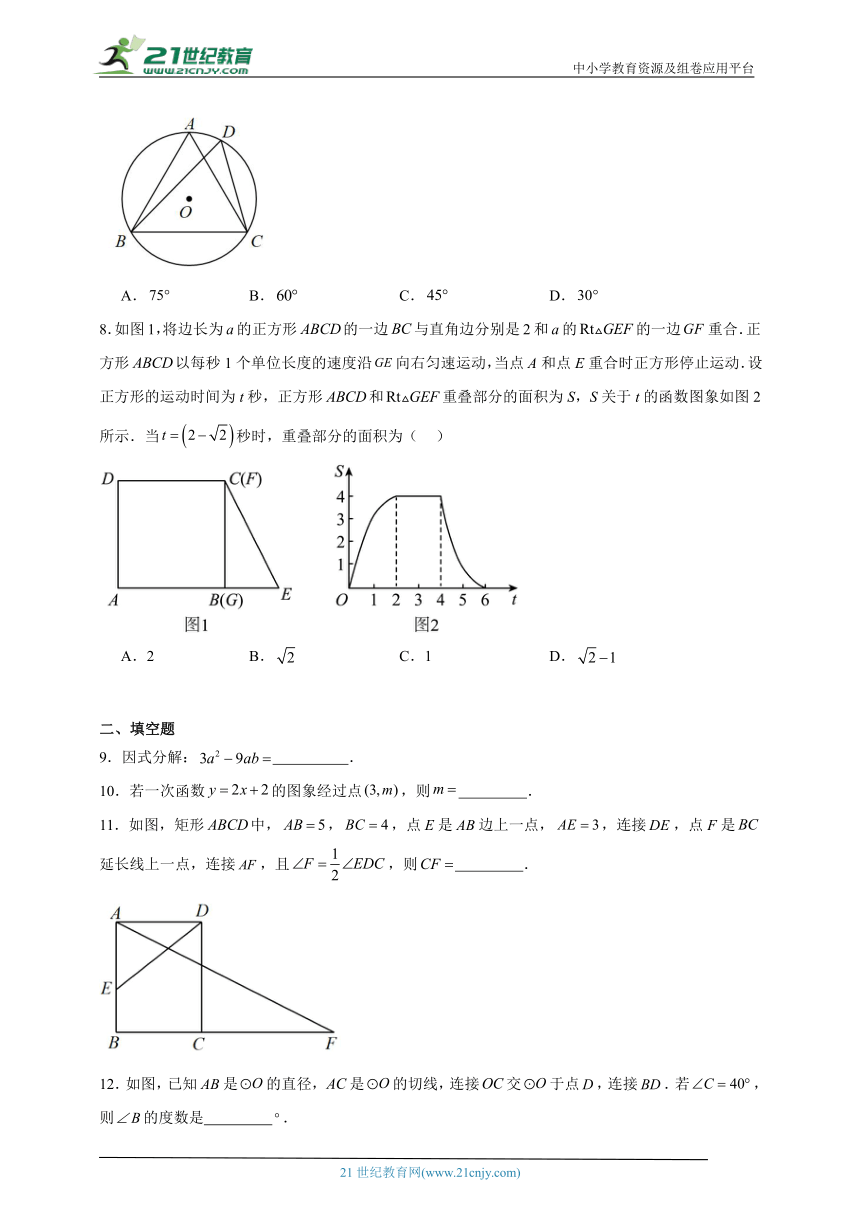
7.如图,、是的两条相交弦,,则( )
A. B. C. D.
8.如图1,将边长为a的正方形的一边与直角边分别是2和a的的一边重合.正方形以每秒1个单位长度的速度沿向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形和重叠部分的面积为S,S关于t的函数图象如图2所示.当秒时,重叠部分的面积为( )
A.2 B. C.1 D.
二、填空题
9.因式分解: .
10.若一次函数的图象经过点,则 .
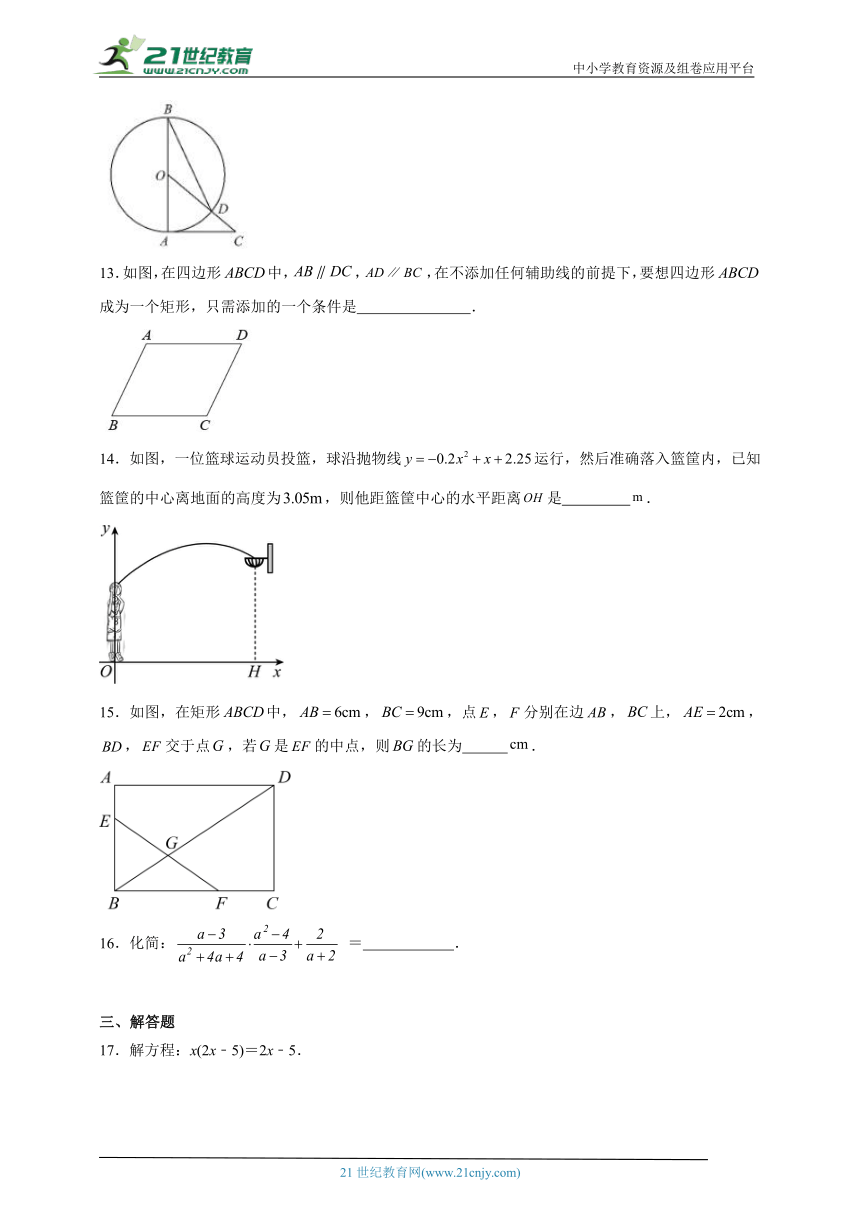
11.如图,矩形中,,,点E是边上一点,,连接,点F是延长线上一点,连接,且,则 .
12.如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是 .
13.如图,在四边形中,,,在不添加任何辅助线的前提下,要想四边形成为一个矩形,只需添加的一个条件是 .
14.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
15.如图,在矩形中,,,点,分别在边,上,,,交于点,若是的中点,则的长为 .
16.化简: = .
三、解答题
17.解方程:x(2x﹣5)=2x﹣5.
18.化简:.
19.如图,在中,.
(1)尺规作图:在边上求一点P,使得.(保留作图痕迹,不写作法)
(2)求证:.
20.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在其南偏西方向上,航行2小时后到达N处,观测到灯塔P在其南偏西方向上,若该船继续向南航行至离灯塔最近的位置(由科学计算器得到,,,.
21.为了响应国家开展“中小学生课后服务”的政策,某学校在课后服务活动中开设了A.书法,B.剪纸,C. 足球,D.乒乓球,共四门课程供学生选修,每门课程被选到的机会均等.
(1)小军选修的课程是篮球这一事件是________.(填序号)
①不可能事件 ②必然事件 ③随机事件
(2)若小军和小彬两位同学各计划选修一门课程,请用列表或画树状图的方法求两人恰好同时选修球类课程的概率.
22.为了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果统计表:
组别 分组(单位:元) 人数
A 4
B 16
C a
D b
E 2
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有 人, , ;
(2)求扇形统计图中扇形C的圆心角的度数;
(3)若该校共有学生1000人,请估计每月零花钱的数额x在范围的人数.
23.如图,一次函数的图象与反比例函数的图象在第一象限交于点,与y轴的负半轴交于点B,且.
(1)求一次函数与反比例函数的表达式;
(2)请直接写出不等式的解集.
24.如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.
25.如图,在中,,于点,过点作于点,交于点.点在边上,且,连接,延长到点,使,连接.
(1)求证:;
(2)试判断的形状,并说明理由;
(3)若,,则________.
26.如图,过点的抛物线的对称轴是直线,点B是抛物线与x轴的一个交点,点C在y轴上,点D是抛物线的顶点,设点P在直线下方且在抛物线上,过点P作y轴的平行线交于点Q.
(1)求a、b的值;
(2)求的最大值;
(3)当是直角三角形时,求的面积.
参考答案:
1.A
【分析】根据绝对值的代数意义即可得出答案.
【详解】解:因为负数的绝对值等于它的相反数,
所以,﹣2023的绝对值等于2023.
故选:A.
【点睛】本题考查了绝对值的代数意义,熟练掌握知识点是本题的关键.
2.C
【分析】先把1062万写成10620000,再根据科学记数法的表示方法解答即可.
【详解】1062万=10620000=
故选:C
【点睛】此题考查了科学记数法的表示方法,科学记数法的表示形式为的形式,其中,n为整数,解题的关键是要确定a的值及n的值.
3.C
【分析】先分别求出两个不等式的解集,再求出解集的公共部分即可.
【详解】,
由①得:x>-3,
由②得:x>2,
所以不等式组的解集是x>2.
故选C.
4.D
【详解】试题分析:将点(m,n)代入函数y=2x+1,得到m和n的关系式,再代入2m﹣n即可解答.
解:将点(m,n)代入函数y=2x+1得,
n=2m+1,
整理得,2m﹣n=﹣1.
故选D.
5.C
【分析】根据判别式的意义得 =42﹣4k≥0,然后解不等式即可.
【详解】根据题意得 =42﹣4k≥0,
解得k≤4.
故选C.
【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与 =b2﹣4ac有如下关系:当 >0时,方程有两个不相等的实数根;当 =0时,方程有两个相等的实数根;当 <0时,方程无实数根.
6.A
【分析】根据“这批椽的价钱为6210文”、“每件椽的运费为3文,剩下的椽的运费恰好等于一株椽的价钱”列出方程解答.
【详解】解:由题意得:,
故选A.
【点睛】本题考查了分式方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,准确的找到等量关系并用方程表示出来是解题的关键.
7.B
【分析】圆周角定理和已知得出,证出为等边三角形,根据等边三角形的性质即可得解.
【详解】解:,,
,
为等边三角形,
,
故选:B.
【点睛】本题考查了圆周角定理等知识,熟练掌握圆周角定理是解题的关键.
8.A
【分析】根据题意得:当时,点B与点E重合;当时,点A与点E重合,,从而得到,可得当秒时,此时,,可得到,从而求出,再由重叠部分的面积为,即可求解.
【详解】解:根据题意得:当时,点B与点E重合;当时,点A与点E重合,,
∴,
∴,
当秒时,如图,此时,,
∴,
∴,即,
∴,
∴重叠部分的面积为.
故选:A
【点睛】本题考查了动点问题的函数图象,利用数形结合思想解答是解题的关键.
9.
【分析】利用提取公因式法因式分解即可
【详解】解:
故答案为:
【点睛】本题考查提取公因式法因式分解,熟练掌握因式分解的方法是关键
10.8
【分析】将点代入一次函数的解析式中即可求出m的值.
【详解】解:由题意知,将点代入一次函数的解析式中,
即:,
解得:.
故答案为:8.
【点睛】本题考查了一次函数的图像和性质,点在图像上,则将点的坐标代入解析式中即可.
11.6
【分析】过点D作DM⊥AF,可证明∠NDM=∠GDM,从而得,DN=DG,设DN=DG=x,列出比例式,求出x的值,进而即可求解.
【详解】解:过点D作DM⊥AF,则∠MAD+∠ADM=90°,
∵在矩形中,∠ADM+∠CDM=90°,
∴∠MAD=∠CDM,
∵AD∥BF,
∴∠F=∠MAD,
∵,
∴∠MAD=,
∴∠CDM=,
∴∠NDM=∠GDM,
∵∠NMD=∠GMD=90°,DM=DM,
∴,
∴DN=DG,
∵,,
∴,
设DN=DG=x,
∵AB∥CD,
∴,
∴,即:,解得:x=2,
∴DN=DG=2,
∵AD∥BF,
∴,
∴,即:,解得:CF=6,
故答案是:6.
【点睛】本题主要考查矩形的性质,全等三角形的性质,勾股定理,相似三角形的判定和性质,添加辅助线,证明,是解题的关键.
12.25
【分析】先由切线的性质可得∠OAC=90°,再根据三角形的内角和定理可求出∠AOD=50°,最后根据“同弧所对的圆周角等于圆心角的一半”即可求出∠B的度数.
【详解】解:∵是的切线,
∴∠OAC=90°
∵,
∴∠AOD=50°,
∴∠B=∠AOD=25°
故答案为:25.
【点睛】本题考查了切线的性质和圆周角定理,掌握圆周角定理是解题的关键.
13.(答案不唯一)
【分析】】先证四边形ABCD是平行四边形,再由矩形的判定即可得出结论.
【详解】解:需添加的一个条件是∠A=90°,理由如下:
∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴平行四边形ABCD是矩形,
故答案为:∠A=90°(答案不唯一).
【点睛】本题考查了矩形的判定、平行四边形的判定与性质等知识,熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键.
14.4
【分析】将代入中可求出x,结合图形可知,即可求出OH.
【详解】解:当时,,解得:或,
结合图形可知:,
故答案为:4
【点睛】本题考查二次函数的实际应用:投球问题,解题的关键是结合函数图形确定x的值.
15.
【分析】根据矩形的性质可得,,,从而可得,然后利用直角三角形斜边上的中线可得,从而可得,进而可得,再证明∽,利用相似三角形的性质可求出的长,最后在中,利用勾股定理求出的长,即可解答.
【详解】解:∵四边形是矩形,
∴,,,
∴,
∵,
∴,
∵是的中点,
∴,
∴,
∴,
∴∽,
∴,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查了相似三角形的判定与性质,勾股定理,矩形的性质,直角三角形斜边上的中线,熟练掌握直角三角形斜边上的中线,以及相似三角形的判定与性质是解题的关键.
16.
【分析】根据分式混合运算的顺序,依次计算即可.
【详解】
=
故答案为
【点睛】本题考查了分式的混合运算,熟练掌握约分,通分,因式分解的技巧是解题的关键.
17.x1=,x2=1
【分析】利用因式分解法解方程即可.
【详解】解:(2x-5)(x-1)=0
x1=,x2=1
【点睛】本题考查因式分解法解一元二次方程,解题的关键是移项后利用提公因式进行因式分解.
18.
【分析】根据分式的混合运算进行化简即可.
【详解】解:原式.
【点睛】本题考查分式的化简,解题的关键是注意运算顺序和约分.
19.(1)见解析
(2)见解析
【分析】(1)作线段的垂直平分线交边即可;
(2)先证,,得,利用两角分别相等的两个三角形全等即可得证.
【详解】(1)解:如图.点P为所求作的点,
(2)证明:∵,
∴,
∵,
∴,
∴.
又∵,
∴∽.
【点睛】本题考查了尺规作线段的垂直平分线以及相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.
20.41.682海里
【分析】如图所示,过点作于点,即该船继续向南航行至离灯塔最近的位置为点处,根据题意可算出的距离,是等腰三角形,在中根据三角函数的计算即可求解.
【详解】解:如图,过点作于点,即该船继续向南航行至离灯塔最近的位置为点处,(海里),
,,,
,
,
是等腰三角形,即海里,
,
(海里).
答:此时轮船离灯塔的距离41.682海里.
【点睛】本题主要考查三角函数的应用,掌握方位角的知识,三角函数的计算方法是解题的关键.
21.(1)①
(2)
【分析】(1)直接根据随机事件的概念:在一定条件下,可能发生也可能不发生的事件进行解答即可;
(2)画树状图展示所有16种等可能的结果数,再找出小明和小刚两人恰好选球类的结果数,然后根据概率公式求解.
【详解】(1)解:小军选修的课程是篮球这一事件是不可能事件,
故答案为:①;
(2)解:
解:画树状图如图:
共有16个等可能的结果数,其中两人恰好同时选修球类的有4种,
则两人恰好同时选修球类的概率是.
【点睛】此题考查了列表法或树状图法求概率.利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.用到的知识点为:概率=所求情况数与总情况数之比.也考查了随机事件.
22.(1)50;28;8
(2)
(3)720人
【分析】(1)根据B组频数及其所占百分比可得总人数,总人数减去其他三个组人数即可求得的值,再用A组人数除以总人数可得m的值;
(2)用乘以C组人数所占比例即可求出圆心角;
(3)总人数乘以样本中B、C组人数之和所占比例即可求解.
【详解】(1)解:调查的总人数是(人),
则(人),
,
则,
故答案为:50;28;8.
(2)解:D组的人数有(人),
则C组的人数有(人),
扇形统计图中扇形C的圆心角度数是;
(3)解:每月零花钱的数额x在范围的人数是(人).
【点睛】本题主要考查了频数统计表和扇形统计图的综合运用,解题关键是读懂统计图,从不同的统计图中得到必要的信息.扇形统计图直接反映部分占总体的百分比大小.
23.(1),
(2)
【分析】(1)根据点坐标求出反比例函数解析式,和点的坐标,待定系数法求出一次函数的解析式;
(2)图象法解出不等式即可.
【详解】(1)解:∵点在反比例函数的图象上,
∴,
∴反比例函数解析式为;
∵,,点B在y轴负半轴上,
∴点.
把点、代入中,
得,
解得:,
∴一次函数的解析式为;
(2)不等式,即:反比例函数在第一象限内,反比例函数值大于一次函数值,
∵,
令,则,
∴点;
由图象知:反比例函数图象在一次函数图象的上方在点的左侧,直线与x轴交点的右侧,
∴不等式的解集为:.
【点睛】本题考查反比例函数与一次函数的综合应用.解题的关键是正确的求出函数解析式,利用数形结合的思想进行求解.
24.(1)见解析;(2)4π﹣8
【分析】(1)连接AD、OD,则AD⊥BC,D为BC中点.OD为中位线,则OD∥AC,根据DF⊥AC可得OD⊥DF得证;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
【详解】(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又AB=AC,
∴D是BC的中点,
连接OD,
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8,
∴S阴影=S扇形AOE﹣S△AOE=4π﹣8,
故答案为4π﹣8.
【点睛】本题考考查了圆的综合知识,圆的切线的证明,等腰三角形的性质和面积计算,扇形的面积计算,平行的性质应用,掌握圆的知识概念是解题的关键.
25.(1)见解析
(2)是等腰直角三角形,理由见解析
(3)
【分析】(1)根据等角的余角相等得出,根据等腰直角三角形的性质得出,证明,根据全等三角形的性质即可得证;
(2)根据平行四边形的性质得出,,进而证明,得出,进而得出是等腰直角三角形;
(3)根据等腰直角三角形的性质可得,则,根据(2)可得,则,进而代入数据即可求解.
【详解】(1)解:证明:∵,,
∴,
∴,
∴,
在中,
∵,
∴.
在和中,
,
∴,
∴.
(2)是等腰直角三角形.
证明:∵四边形是平行四边形,
∴,.
∵,,
∴.
∵,
∴,
∴,
∴.
∵,,
∴.
∴,
∴,
∵,
∴,
∴是等腰直角三角形.
(3)∵是等腰直角三角形.
∴,
即,
由(2)知,
∴
∴.
即,
解得
【点睛】本题考查了平行四边形的性质,等腰三角形的性质与判定,勾股定理,全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
26.(1)
(2)
(3)或
【分析】(1)用待定系数法即可求得;
(2)求出直线的解析式,设,则,则可得关于x的二次函数,即可求得的最大值;
(3)设D点的坐标为,求出,分三种情况考虑,利用勾股定理建立方程求出m的值,即可求得的面积.
【详解】(1)解:∵过点的抛物线的对称轴是直线,
∴,解得,
故.
(2)解:设直线过点,可得直线.
由(1)可得抛物线,
设,则,
∴,
∴当时,最大,最大值为.
(3)解:设点C的坐标是.由(1)可得抛物线,
∴抛物线的顶点D的坐标是,点B的坐标是.
则,,,
①当时,有.
∴,解得,
∴.
②当时,有.
∴,解得,
∴.
③当时,有.
∴,此方程无解.
综上所述,当为直角三角形时,的面积是或.
【点睛】本题是二次函数与几何的综合,考查了二次函数的图象与性质,勾股定理,涉及分类讨论的思想,综合运用这些知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
重庆市2024届中考数学一轮模拟卷
学校:___________姓名:___________班级:___________考号:___________
题号 一 二 三 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.实数﹣2023的绝对值是( )
A.2023 B.﹣2023 C. D.
2.近年来出生人口持续走低,即使国家开放三孩,也缓解不了颓势,2022年我国出生人口是1062万人,数据1062万用科学记数法表示应为( )
A. B. C. D.
3.不等式组的解集是( )
A.x>﹣3 B.x<﹣3 C.x>2 D.x<2
4.若点(m,n)在函数y=2x+1的图象上,则2m﹣n的值是( )
A.2 B.﹣2 C.1 D.﹣1
5.关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
A.k≤﹣4 B.k<﹣4 C.k≤4 D.k<4
6.我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )
A. B. C. D.
7.如图,、是的两条相交弦,,则( )
A. B. C. D.
8.如图1,将边长为a的正方形的一边与直角边分别是2和a的的一边重合.正方形以每秒1个单位长度的速度沿向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形和重叠部分的面积为S,S关于t的函数图象如图2所示.当秒时,重叠部分的面积为( )
A.2 B. C.1 D.
二、填空题
9.因式分解: .
10.若一次函数的图象经过点,则 .
11.如图,矩形中,,,点E是边上一点,,连接,点F是延长线上一点,连接,且,则 .
12.如图,已知是的直径,是的切线,连接交于点,连接.若,则的度数是 .
13.如图,在四边形中,,,在不添加任何辅助线的前提下,要想四边形成为一个矩形,只需添加的一个条件是 .
14.如图,一位篮球运动员投篮,球沿抛物线运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为,则他距篮筐中心的水平距离是 .
15.如图,在矩形中,,,点,分别在边,上,,,交于点,若是的中点,则的长为 .
16.化简: = .
三、解答题
17.解方程:x(2x﹣5)=2x﹣5.
18.化简:.
19.如图,在中,.
(1)尺规作图:在边上求一点P,使得.(保留作图痕迹,不写作法)
(2)求证:.
20.如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在其南偏西方向上,航行2小时后到达N处,观测到灯塔P在其南偏西方向上,若该船继续向南航行至离灯塔最近的位置(由科学计算器得到,,,.
21.为了响应国家开展“中小学生课后服务”的政策,某学校在课后服务活动中开设了A.书法,B.剪纸,C. 足球,D.乒乓球,共四门课程供学生选修,每门课程被选到的机会均等.
(1)小军选修的课程是篮球这一事件是________.(填序号)
①不可能事件 ②必然事件 ③随机事件
(2)若小军和小彬两位同学各计划选修一门课程,请用列表或画树状图的方法求两人恰好同时选修球类课程的概率.
22.为了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果统计表:
组别 分组(单位:元) 人数
A 4
B 16
C a
D b
E 2
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有 人, , ;
(2)求扇形统计图中扇形C的圆心角的度数;
(3)若该校共有学生1000人,请估计每月零花钱的数额x在范围的人数.
23.如图,一次函数的图象与反比例函数的图象在第一象限交于点,与y轴的负半轴交于点B,且.
(1)求一次函数与反比例函数的表达式;
(2)请直接写出不等式的解集.
24.如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.
25.如图,在中,,于点,过点作于点,交于点.点在边上,且,连接,延长到点,使,连接.
(1)求证:;
(2)试判断的形状,并说明理由;
(3)若,,则________.
26.如图,过点的抛物线的对称轴是直线,点B是抛物线与x轴的一个交点,点C在y轴上,点D是抛物线的顶点,设点P在直线下方且在抛物线上,过点P作y轴的平行线交于点Q.
(1)求a、b的值;
(2)求的最大值;
(3)当是直角三角形时,求的面积.
参考答案:
1.A
【分析】根据绝对值的代数意义即可得出答案.
【详解】解:因为负数的绝对值等于它的相反数,
所以,﹣2023的绝对值等于2023.
故选:A.
【点睛】本题考查了绝对值的代数意义,熟练掌握知识点是本题的关键.
2.C
【分析】先把1062万写成10620000,再根据科学记数法的表示方法解答即可.
【详解】1062万=10620000=
故选:C
【点睛】此题考查了科学记数法的表示方法,科学记数法的表示形式为的形式,其中,n为整数,解题的关键是要确定a的值及n的值.
3.C
【分析】先分别求出两个不等式的解集,再求出解集的公共部分即可.
【详解】,
由①得:x>-3,
由②得:x>2,
所以不等式组的解集是x>2.
故选C.
4.D
【详解】试题分析:将点(m,n)代入函数y=2x+1,得到m和n的关系式,再代入2m﹣n即可解答.
解:将点(m,n)代入函数y=2x+1得,
n=2m+1,
整理得,2m﹣n=﹣1.
故选D.
5.C
【分析】根据判别式的意义得 =42﹣4k≥0,然后解不等式即可.
【详解】根据题意得 =42﹣4k≥0,
解得k≤4.
故选C.
【点睛】本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与 =b2﹣4ac有如下关系:当 >0时,方程有两个不相等的实数根;当 =0时,方程有两个相等的实数根;当 <0时,方程无实数根.
6.A
【分析】根据“这批椽的价钱为6210文”、“每件椽的运费为3文,剩下的椽的运费恰好等于一株椽的价钱”列出方程解答.
【详解】解:由题意得:,
故选A.
【点睛】本题考查了分式方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,准确的找到等量关系并用方程表示出来是解题的关键.
7.B
【分析】圆周角定理和已知得出,证出为等边三角形,根据等边三角形的性质即可得解.
【详解】解:,,
,
为等边三角形,
,
故选:B.
【点睛】本题考查了圆周角定理等知识,熟练掌握圆周角定理是解题的关键.
8.A
【分析】根据题意得:当时,点B与点E重合;当时,点A与点E重合,,从而得到,可得当秒时,此时,,可得到,从而求出,再由重叠部分的面积为,即可求解.
【详解】解:根据题意得:当时,点B与点E重合;当时,点A与点E重合,,
∴,
∴,
当秒时,如图,此时,,
∴,
∴,即,
∴,
∴重叠部分的面积为.
故选:A
【点睛】本题考查了动点问题的函数图象,利用数形结合思想解答是解题的关键.
9.
【分析】利用提取公因式法因式分解即可
【详解】解:
故答案为:
【点睛】本题考查提取公因式法因式分解,熟练掌握因式分解的方法是关键
10.8
【分析】将点代入一次函数的解析式中即可求出m的值.
【详解】解:由题意知,将点代入一次函数的解析式中,
即:,
解得:.
故答案为:8.
【点睛】本题考查了一次函数的图像和性质,点在图像上,则将点的坐标代入解析式中即可.
11.6
【分析】过点D作DM⊥AF,可证明∠NDM=∠GDM,从而得,DN=DG,设DN=DG=x,列出比例式,求出x的值,进而即可求解.
【详解】解:过点D作DM⊥AF,则∠MAD+∠ADM=90°,
∵在矩形中,∠ADM+∠CDM=90°,
∴∠MAD=∠CDM,
∵AD∥BF,
∴∠F=∠MAD,
∵,
∴∠MAD=,
∴∠CDM=,
∴∠NDM=∠GDM,
∵∠NMD=∠GMD=90°,DM=DM,
∴,
∴DN=DG,
∵,,
∴,
设DN=DG=x,
∵AB∥CD,
∴,
∴,即:,解得:x=2,
∴DN=DG=2,
∵AD∥BF,
∴,
∴,即:,解得:CF=6,
故答案是:6.
【点睛】本题主要考查矩形的性质,全等三角形的性质,勾股定理,相似三角形的判定和性质,添加辅助线,证明,是解题的关键.
12.25
【分析】先由切线的性质可得∠OAC=90°,再根据三角形的内角和定理可求出∠AOD=50°,最后根据“同弧所对的圆周角等于圆心角的一半”即可求出∠B的度数.
【详解】解:∵是的切线,
∴∠OAC=90°
∵,
∴∠AOD=50°,
∴∠B=∠AOD=25°
故答案为:25.
【点睛】本题考查了切线的性质和圆周角定理,掌握圆周角定理是解题的关键.
13.(答案不唯一)
【分析】】先证四边形ABCD是平行四边形,再由矩形的判定即可得出结论.
【详解】解:需添加的一个条件是∠A=90°,理由如下:
∵AB∥DC,AD∥BC,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴平行四边形ABCD是矩形,
故答案为:∠A=90°(答案不唯一).
【点睛】本题考查了矩形的判定、平行四边形的判定与性质等知识,熟练掌握矩形的判定和平行四边形的判定与性质是解题的关键.
14.4
【分析】将代入中可求出x,结合图形可知,即可求出OH.
【详解】解:当时,,解得:或,
结合图形可知:,
故答案为:4
【点睛】本题考查二次函数的实际应用:投球问题,解题的关键是结合函数图形确定x的值.
15.
【分析】根据矩形的性质可得,,,从而可得,然后利用直角三角形斜边上的中线可得,从而可得,进而可得,再证明∽,利用相似三角形的性质可求出的长,最后在中,利用勾股定理求出的长,即可解答.
【详解】解:∵四边形是矩形,
∴,,,
∴,
∵,
∴,
∵是的中点,
∴,
∴,
∴,
∴∽,
∴,
∴,
∴,
∴,
∴,
故答案为:.
【点睛】本题考查了相似三角形的判定与性质,勾股定理,矩形的性质,直角三角形斜边上的中线,熟练掌握直角三角形斜边上的中线,以及相似三角形的判定与性质是解题的关键.
16.
【分析】根据分式混合运算的顺序,依次计算即可.
【详解】
=
故答案为
【点睛】本题考查了分式的混合运算,熟练掌握约分,通分,因式分解的技巧是解题的关键.
17.x1=,x2=1
【分析】利用因式分解法解方程即可.
【详解】解:(2x-5)(x-1)=0
x1=,x2=1
【点睛】本题考查因式分解法解一元二次方程,解题的关键是移项后利用提公因式进行因式分解.
18.
【分析】根据分式的混合运算进行化简即可.
【详解】解:原式.
【点睛】本题考查分式的化简,解题的关键是注意运算顺序和约分.
19.(1)见解析
(2)见解析
【分析】(1)作线段的垂直平分线交边即可;
(2)先证,,得,利用两角分别相等的两个三角形全等即可得证.
【详解】(1)解:如图.点P为所求作的点,
(2)证明:∵,
∴,
∵,
∴,
∴.
又∵,
∴∽.
【点睛】本题考查了尺规作线段的垂直平分线以及相似三角形的判定,熟练掌握相似三角形的判定是解题的关键.
20.41.682海里
【分析】如图所示,过点作于点,即该船继续向南航行至离灯塔最近的位置为点处,根据题意可算出的距离,是等腰三角形,在中根据三角函数的计算即可求解.
【详解】解:如图,过点作于点,即该船继续向南航行至离灯塔最近的位置为点处,(海里),
,,,
,
,
是等腰三角形,即海里,
,
(海里).
答:此时轮船离灯塔的距离41.682海里.
【点睛】本题主要考查三角函数的应用,掌握方位角的知识,三角函数的计算方法是解题的关键.
21.(1)①
(2)
【分析】(1)直接根据随机事件的概念:在一定条件下,可能发生也可能不发生的事件进行解答即可;
(2)画树状图展示所有16种等可能的结果数,再找出小明和小刚两人恰好选球类的结果数,然后根据概率公式求解.
【详解】(1)解:小军选修的课程是篮球这一事件是不可能事件,
故答案为:①;
(2)解:
解:画树状图如图:
共有16个等可能的结果数,其中两人恰好同时选修球类的有4种,
则两人恰好同时选修球类的概率是.
【点睛】此题考查了列表法或树状图法求概率.利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.用到的知识点为:概率=所求情况数与总情况数之比.也考查了随机事件.
22.(1)50;28;8
(2)
(3)720人
【分析】(1)根据B组频数及其所占百分比可得总人数,总人数减去其他三个组人数即可求得的值,再用A组人数除以总人数可得m的值;
(2)用乘以C组人数所占比例即可求出圆心角;
(3)总人数乘以样本中B、C组人数之和所占比例即可求解.
【详解】(1)解:调查的总人数是(人),
则(人),
,
则,
故答案为:50;28;8.
(2)解:D组的人数有(人),
则C组的人数有(人),
扇形统计图中扇形C的圆心角度数是;
(3)解:每月零花钱的数额x在范围的人数是(人).
【点睛】本题主要考查了频数统计表和扇形统计图的综合运用,解题关键是读懂统计图,从不同的统计图中得到必要的信息.扇形统计图直接反映部分占总体的百分比大小.
23.(1),
(2)
【分析】(1)根据点坐标求出反比例函数解析式,和点的坐标,待定系数法求出一次函数的解析式;
(2)图象法解出不等式即可.
【详解】(1)解:∵点在反比例函数的图象上,
∴,
∴反比例函数解析式为;
∵,,点B在y轴负半轴上,
∴点.
把点、代入中,
得,
解得:,
∴一次函数的解析式为;
(2)不等式,即:反比例函数在第一象限内,反比例函数值大于一次函数值,
∵,
令,则,
∴点;
由图象知:反比例函数图象在一次函数图象的上方在点的左侧,直线与x轴交点的右侧,
∴不等式的解集为:.
【点睛】本题考查反比例函数与一次函数的综合应用.解题的关键是正确的求出函数解析式,利用数形结合的思想进行求解.
24.(1)见解析;(2)4π﹣8
【分析】(1)连接AD、OD,则AD⊥BC,D为BC中点.OD为中位线,则OD∥AC,根据DF⊥AC可得OD⊥DF得证;
(2)连接OE,利用(1)的结论得∠ABC=∠ACB=67.5°,易得∠BAC=45°,得出∠AOE=90°,利用扇形的面积公式和三角形的面积公式得出结论.
【详解】(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
又AB=AC,
∴D是BC的中点,
连接OD,
由中位线定理,知DO∥AC,
又DF⊥AC,
∴DF⊥OD,
∴DF是⊙O的切线;
(2)连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴S扇形AOE=4π,S△AOE=8,
∴S阴影=S扇形AOE﹣S△AOE=4π﹣8,
故答案为4π﹣8.
【点睛】本题考考查了圆的综合知识,圆的切线的证明,等腰三角形的性质和面积计算,扇形的面积计算,平行的性质应用,掌握圆的知识概念是解题的关键.
25.(1)见解析
(2)是等腰直角三角形,理由见解析
(3)
【分析】(1)根据等角的余角相等得出,根据等腰直角三角形的性质得出,证明,根据全等三角形的性质即可得证;
(2)根据平行四边形的性质得出,,进而证明,得出,进而得出是等腰直角三角形;
(3)根据等腰直角三角形的性质可得,则,根据(2)可得,则,进而代入数据即可求解.
【详解】(1)解:证明:∵,,
∴,
∴,
∴,
在中,
∵,
∴.
在和中,
,
∴,
∴.
(2)是等腰直角三角形.
证明:∵四边形是平行四边形,
∴,.
∵,,
∴.
∵,
∴,
∴,
∴.
∵,,
∴.
∴,
∴,
∵,
∴,
∴是等腰直角三角形.
(3)∵是等腰直角三角形.
∴,
即,
由(2)知,
∴
∴.
即,
解得
【点睛】本题考查了平行四边形的性质,等腰三角形的性质与判定,勾股定理,全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.
26.(1)
(2)
(3)或
【分析】(1)用待定系数法即可求得;
(2)求出直线的解析式,设,则,则可得关于x的二次函数,即可求得的最大值;
(3)设D点的坐标为,求出,分三种情况考虑,利用勾股定理建立方程求出m的值,即可求得的面积.
【详解】(1)解:∵过点的抛物线的对称轴是直线,
∴,解得,
故.
(2)解:设直线过点,可得直线.
由(1)可得抛物线,
设,则,
∴,
∴当时,最大,最大值为.
(3)解:设点C的坐标是.由(1)可得抛物线,
∴抛物线的顶点D的坐标是,点B的坐标是.
则,,,
①当时,有.
∴,解得,
∴.
②当时,有.
∴,解得,
∴.
③当时,有.
∴,此方程无解.
综上所述,当为直角三角形时,的面积是或.
【点睛】本题是二次函数与几何的综合,考查了二次函数的图象与性质,勾股定理,涉及分类讨论的思想,综合运用这些知识是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
