数学人教A版(2019)选择性必修第三册6.3.1二项式定理 课件(共41张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.3.1二项式定理 课件(共41张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 07:44:23 | ||
图片预览


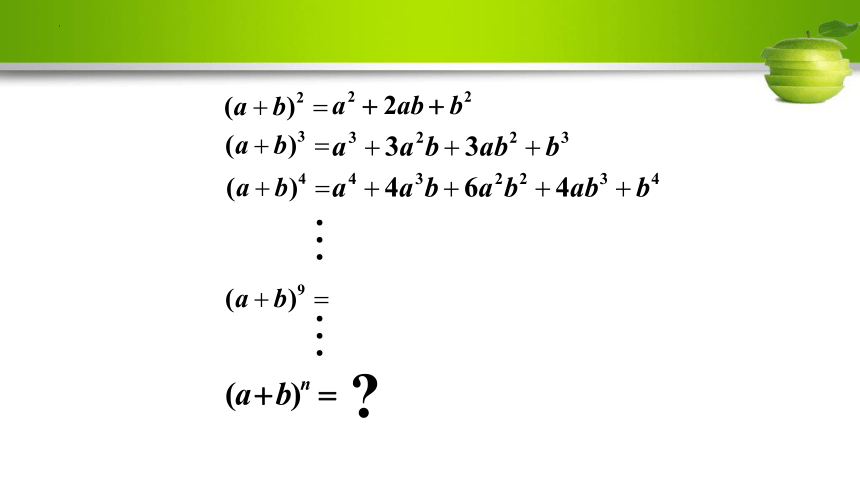






文档简介
(共41张PPT)
二项式定理
艾萨克·牛顿 Isaac Newton (1643—1727) 英国科学家.他被誉为人类历史上最伟大的科学家之一.他不仅是一位物理学家、天文学家,还是一位伟大的数学家.
问题1:
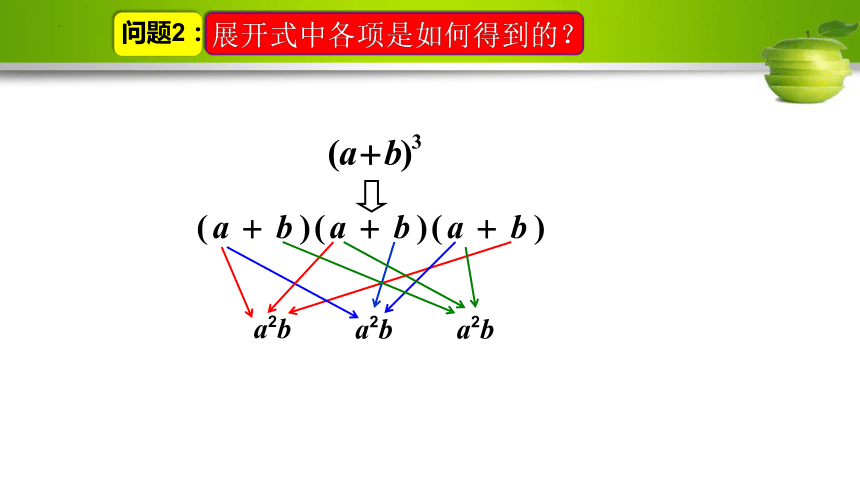
问题2:
a2
ab
ba
b2
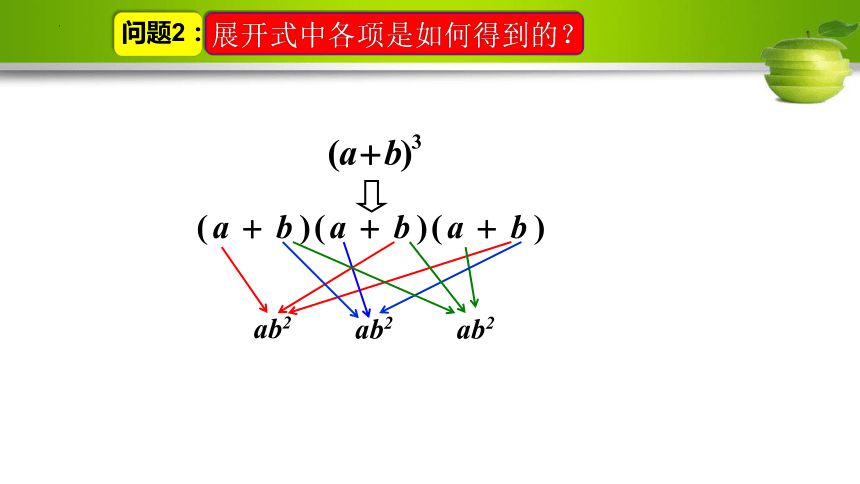
问题2:
问题2:
a3
问题2:
a2b
a2b
a2b
问题2:
ab2
ab2
ab2
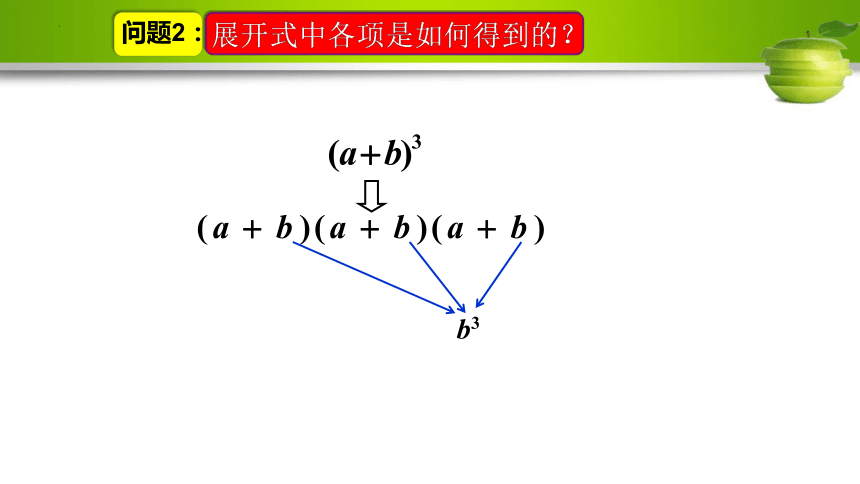
问题2:
b3
问题2:
a3
a2b
ab2
b3
问题2:
问题2:
问题2:
问题2:
问题2:
a4
问题2:
问题2:
a4
a3b
ab3
b4
a2b2
问题2:
问题2:
问题2:
问题3:
a2
ab
ba
b2
1个
b2
1个
a2
2个
ab
问题3:
a3
1个a3
问题3:
a2b
a2b
a2b
3个a2b
问题3:
ab2
3个ab2
问题3:
ab2
ab2
b3
1个b3
问题3:
1个a4
a4
a3b
4个a3b
问题3:
a2b2
6个a2b2
问题3:
a2b2
6个a2b2
问题3:
a3b
4个a3b
ab3
4个ab3
b4
1个b4
a4
1个a4
问题4:
证明:
(项的结构)
证明:
(项的系数)
问题4:
(1)展开式共有n+1项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;
字母b按升幂排列,次数由0递增到n.
(4)二项展开式中,系数 叫作二项式系数,即
(3)二项展开式的通项:
二项式定理
试一试
例1: 求 的展开式.
解:
想一想
求展开式第6项的系数.
例2:求 展开式中第6项的二项式系数.
二项式系数为 .
解:
注意
某项的二项式系数与该项的系数的区别
所以系数为-252.
练习: 求 的展开式中 的系数.
解:
回顾总结
知识方面
二项式定理,通项,二项式系数;
思想方法
由特殊到一般;观察、归纳、类比、猜想、证明.
课下作业
谢 谢!
二项式定理
艾萨克·牛顿 Isaac Newton (1643—1727) 英国科学家.他被誉为人类历史上最伟大的科学家之一.他不仅是一位物理学家、天文学家,还是一位伟大的数学家.
问题1:
问题2:
a2
ab
ba
b2
问题2:
问题2:
a3
问题2:
a2b
a2b
a2b
问题2:
ab2
ab2
ab2
问题2:
b3
问题2:
a3
a2b
ab2
b3
问题2:
问题2:
问题2:
问题2:
问题2:
a4
问题2:
问题2:
a4
a3b
ab3
b4
a2b2
问题2:
问题2:
问题2:
问题3:
a2
ab
ba
b2
1个
b2
1个
a2
2个
ab
问题3:
a3
1个a3
问题3:
a2b
a2b
a2b
3个a2b
问题3:
ab2
3个ab2
问题3:
ab2
ab2
b3
1个b3
问题3:
1个a4
a4
a3b
4个a3b
问题3:
a2b2
6个a2b2
问题3:
a2b2
6个a2b2
问题3:
a3b
4个a3b
ab3
4个ab3
b4
1个b4
a4
1个a4
问题4:
证明:
(项的结构)
证明:
(项的系数)
问题4:
(1)展开式共有n+1项.
(2)各项的次数都等于二项式的次数n;
字母a按降幂排列,次数由n递减到0;
字母b按升幂排列,次数由0递增到n.
(4)二项展开式中,系数 叫作二项式系数,即
(3)二项展开式的通项:
二项式定理
试一试
例1: 求 的展开式.
解:
想一想
求展开式第6项的系数.
例2:求 展开式中第6项的二项式系数.
二项式系数为 .
解:
注意
某项的二项式系数与该项的系数的区别
所以系数为-252.
练习: 求 的展开式中 的系数.
解:
回顾总结
知识方面
二项式定理,通项,二项式系数;
思想方法
由特殊到一般;观察、归纳、类比、猜想、证明.
课下作业
谢 谢!
