必考专题:长方体(一)应用题-数学五年级下册北师大版(含解析)
文档属性
| 名称 | 必考专题:长方体(一)应用题-数学五年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 361.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-02 11:11:10 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
必考专题:长方体(一)应用题-数学五年级下册北师大版
1.元宵节,奇思要制作一个底面是边长25cm的正方形,高是40cm的长方体灯笼,至少需要准备多少米的木条来搭这个灯笼框架?
2.做一个无盖的棱长为6分米的正方体铁盒,至少需要多大的面积的铁皮?(盖子的接口处可以忽略不计)
3.游泳中心新建了一个长50米、宽25米、深2米的游泳池。现要在游泳池四周和底面都贴上瓷砖,如果每平方米需要32元,一共需要多少元?
4.一个实验室长12米,宽9米,高4米。要粉刷实验室的天花板和四面墙壁,除去门窗和黑板的面积27.5平方米,平均每平方米用石灰0.2千克,一共需要石灰多少千克?
5.把一个长方体用三种不同的方法切成两个完全相同的长方体,结果它们的表面积分别增加了40、48、60平方厘米。原来的长方体的表面积是多少平方厘米?
6.有三个同样的长方体盒子,长10厘米,宽8厘米,高2厘米。现在要把这三个盒子包装在一起,最少需要多少平方厘米的包装纸?
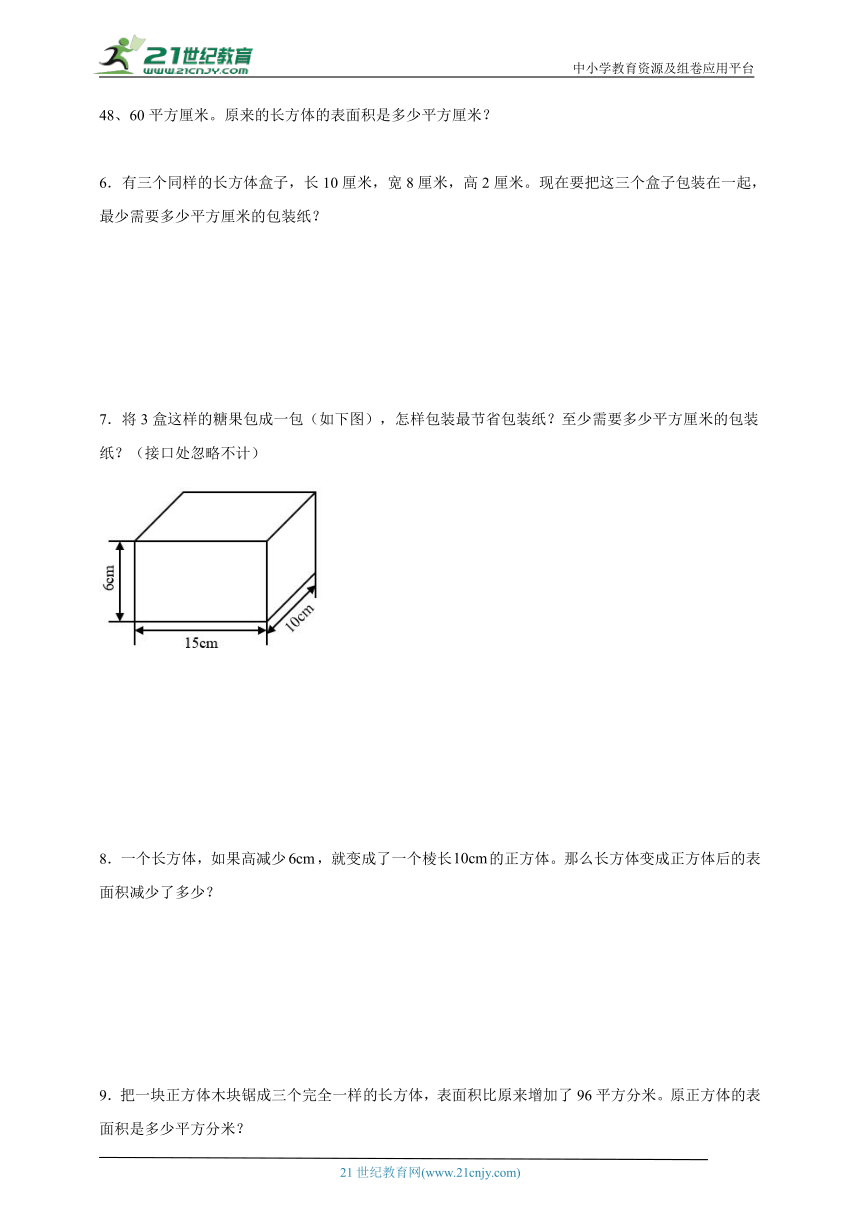
7.将3盒这样的糖果包成一包(如下图),怎样包装最节省包装纸?至少需要多少平方厘米的包装纸?(接口处忽略不计)
8.一个长方体,如果高减少,就变成了一个棱长的正方体。那么长方体变成正方体后的表面积减少了多少?
9.把一块正方体木块锯成三个完全一样的长方体,表面积比原来增加了96平方分米。原正方体的表面积是多少平方分米?
10.有A、B、C三种规格的纸板各四张,从中选六张可做成一个长方体,这个长方体的表面积是多少?
11.一个底面是正方形的长方体铁桶,把它的侧面展开正好得到一个边长为40厘米的正方形。如果铁桶内装半桶水,与水接触的面的面积是多少?
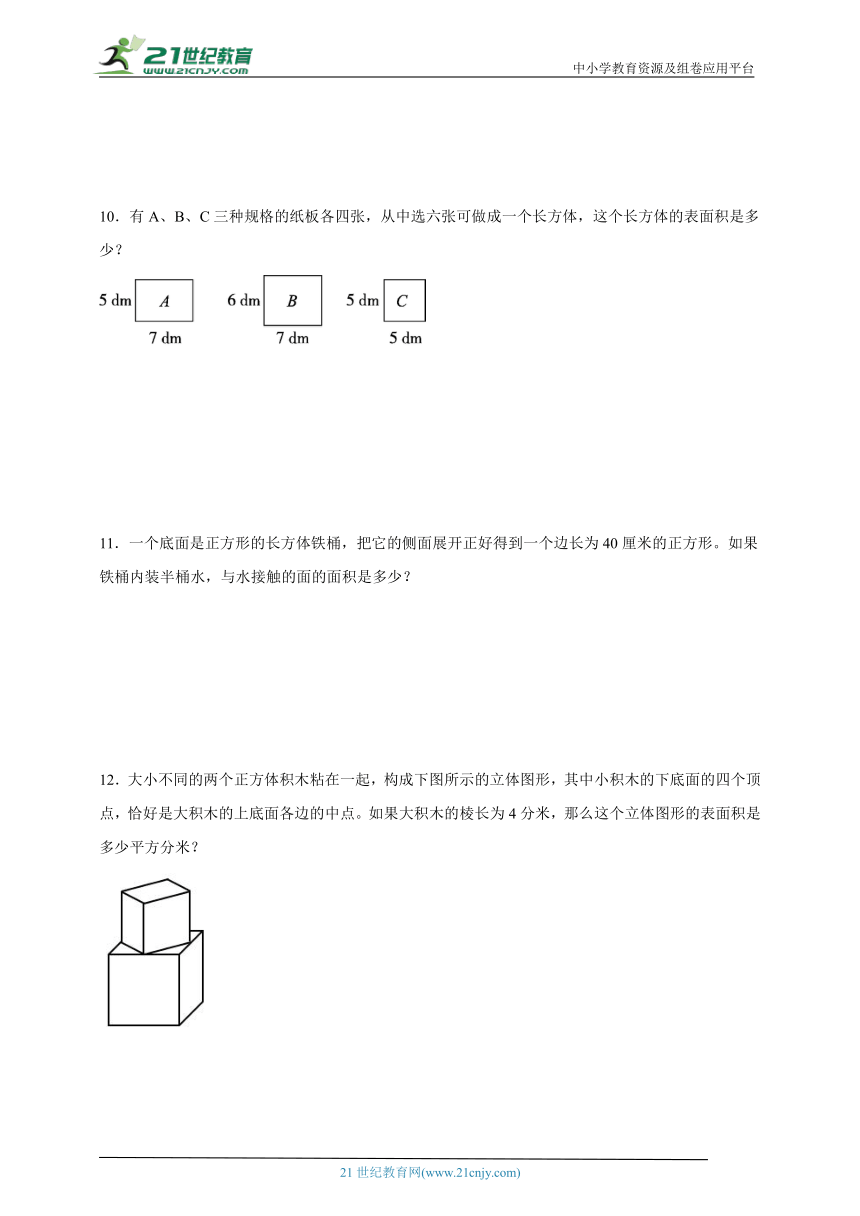
12.大小不同的两个正方体积木粘在一起,构成下图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点。如果大积木的棱长为4分米,那么这个立体图形的表面积是多少平方分米?
13.黄老师给贫困山区的孩子买了4本同样的《十万个为什么》,每本书的长25厘米、宽18厘米、厚3厘米。包装这些书至少需要多大面积的包装纸?
14.一个长方体礼品盒,长28厘米,宽20厘米,高5厘米。如果包装这个礼品盒的用纸是其表面积的倍,至少要用多少平方厘米的包装纸?
15.游乐园里新增了一批垃圾箱,形状如图。它是由两个正方体组成的,其中小正方体的棱长是2dm,大正方体的棱长是5dm。小正方体无盖,便于人们扔垃圾。制作这样一个垃圾箱,至少需要多少平方分米的铁皮?
16.新世界中英文学校有四节长方体的通风管道,长宽各是5分米,高2米。做这些通风管道共用铁皮多少平方米?
17.饼干盒的长和宽都是10厘米,高是15厘米,要在盒子的四周贴上商标,印制1000张这样的商标,至少需要多少平方米商标纸?
18.加工厂要加工一批长方体立式空调机罩(没有底面),已知每台空调长50厘米,宽40厘米,高160厘米,做40个这样的空调机套至少要用多少平方米的布?
参考答案:
1.3.6米
【分析】根据“长方体的棱长和=(长+宽+高)×4”,即可求出至少需要准备多少米的木条来搭这个灯笼框架。
【详解】(25+25+40)×4
=90×4
=360(厘米)
360厘米=3.6米
答:至少需要准备3.6米的木条来搭这个灯笼框架。
【点睛】解答本题关键是熟练运用长方体的棱长和公式。注意单位的转化。
2.180平方分米
【分析】根据题意可知,求至少需要多大的面积的铁皮,就是求这个无盖正方体5个面的面积和,根据正方体表面积公式:表面积=棱长×棱长×5,代入数据,即可解答。
【详解】6×6×5
=36×5
=180(平方分米)
答:至少需要180平方分米大的面积的铁皮。
【点睛】本题考查正方体表面积公式的应用,关键是熟记公式。
3.49600元
【分析】根据题意,先求贴瓷砖的面积,即长方体游泳池5个面积的面积和;根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,求出贴瓷砖的面积,再乘32,即可求出需要的钱数。
【详解】[50×25+(50×2+25×2)×2]×32
=[1250+(100+50)×2]×32
=[1250+150×2]×32
=[1250+300]×32
=1550×32
=49600(元)
答:一共需要49600元。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
4.49.7千克
【详解】[(12×4+9×4)×2+12×9-27.5]×0.2
=[(48+36)×2+108-27.5]×0.2
=(84×2+108-27.5)×0.2
=(168+108-27.5)×0.2
=(276-27.5)×0.2
=248.5×0.2
=49.7(千克)
答:一共需要石灰49.7千克。
5.148平方厘米
【分析】根据题意可知,把一个长方体切成两个完全相同的长方体,两个小长方体的表面积和比原来长方体的表面积增加两个切面的面积,用三种不同的方法切成两个完全相同的长方体,由此可分析出原长方体三个面的面积,把三种切法增加的面相加,就是原长方体的表面积。据此列式解答即可。
【详解】40+48+60
=88+60
=148(平方厘米)
答:原来的长方体的表面积是148平方厘米。
【点睛】此题的重点是要理解三种切法增加的面积和就是长方体的表面积。
6.376平方厘米
【分析】把三个长方体盒子叠在一起,有3种方式,重叠面积最大的叠法最省包装纸,即重叠底面时最省包装纸,据此解答。
【详解】因为三个面中底面最大,所以重合放在一起最省包装纸。
长方体的长是10厘米,宽是8厘米,高是2×3=6(厘米)
(10×8+10×6+8×6)×2
=(80+60+48)×2
=(140+48)×2
=188×2
=376(平方厘米)
答:最少需要376平方厘米的包装纸。
【点睛】最大面重合,得到的长方体的表面积最小,最小面重合,得到的长方体表面积最大。
7.将15厘米和10厘米这两个面相互叠加包装起来最节省包装纸;1200平方厘米
【分析】根据题意,将最大的面(15×10)互相叠加包装起来最省包装纸,根据长方体的表面积公式S=(ab+ah+bh)×2,代入数据解答即可。
【详解】由分析得:
将15厘米和10厘米这两个面相互叠加包装起来最节省包装纸。
(平方厘米)
答:至少需要1200平方厘米的包装纸。
【点睛】本题主要考查长方体表面积的实际应用与立体图形的拼接问题,关键是熟记公式,同时明确重合面越大越省包装纸。
8.240平方厘米
【分析】根据题意,一个长方体如果高减少6cm,就变成一个棱长10cm的正方体,长方体的长=长方体的宽=正方体棱长=10cm;求减少部分的面积,就是一个长是10cm,宽是10cm,高是6cm的长方体的侧面积;且这四个面相等;根据长方形面积公式:长×高,代入数据,即可解答。
【详解】10×6×4
=60×4
=240(cm2)
答:长方体变成正方体后的表面积减少了240平方厘米。
【点睛】解答本题的关键是明确减少后的长方体的长与宽和正方体棱长的关系。
9.144平方分米
【分析】正方体锯成三个完全一样的长方体,表面积多了四个正方形的面积。用除法求出一个正方形的面积,再根据“正方体表面积=正方形面积×6”计算即可。
【详解】96÷4×6
=24×6
=144(平方分米)
答:原来正方体的表面积是144平方分米。
【点睛】本题考查的是正方形表面积的计算,明确正方体锯成长方体,表面积增加的面积是几个正方形的面积,是解答本题的关键。
10.选四张A、两张C可做成一个长方体。190平方分米
【分析】根据长方体的特征,相对的面完全相同,把12条棱平均分成3组,分别是长、宽、高,由此可知,需要选四张A、两张C组成一个长方体,长方体的表面积就是6个面的面积之和,据此解答。
【详解】选四张A、两张C可做成一个长方体。
5×5×2+5×7×4
=50+140
=190(平方分米)
答:长方体的表面积是190平方分米。
【点睛】此题考查了长方体的特征以及表面积计算,根据长方体特征,先选择出所需要的纸板是解题关键。
11.900平方厘米
【分析】这是一个无盖桶,与水接触面的面积即桶的底面和四个侧面面积,根据桶的侧面展开图是边长为40厘米的正方形,求出有水部分的长和宽。根据长方体的面积公式求出一个面的面积再乘4即可得到四个侧面的面积,再加桶的底面积即可得到答案。
【详解】40÷4=10(厘米)
底面面积:10×10=100(平方厘米)
侧面面积:10×20×4=800(平方厘米)
与水接触的面积:10×10+10×20×4=900(平方厘米)
答:与水接触的面的面积是900平方厘米。
【点睛】关键是弄清楚与水接触的面是什么,再根据侧面展开图为边长是40厘米的正方形这个线索进行求解。
12.128平方分米
【分析】如图,因为小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点,所以大正方体一个面的面积是小正方体一个面的面积的2倍,因此,这个立方体图形的表面积=大正方体的表面积+小正方体四个侧面的面积;据此解答。
【详解】由分析得:
6×4×4+4×(4×4÷2)
=96+4×8
=96+32
=128(平方分米)
答:那么这个立体图形的表面积是128平方分米。
【点睛】本题主要考查组合体的表面积计算,关键是明确大正方体一个面的面积是小正方体一个面的面积的2倍。
13.1932平方厘米
【分析】当把4本书一本一本封面向上放在一起最节省包装纸,即此时的长是25厘米,宽是18厘米,高是:3×4=12(厘米),根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,把数代入公式即可求解。
【详解】由分析可知:把4本书叠放在一起最节省包装纸。
此时的高:4×3=12(厘米)
(25×18+25×12+18×12)×2
=(450+300+216)×2
=966×2
=1932(平方厘米)
答:包装这些书至少需要1932平方厘米的包装纸。
【点睛】本题主要考查长方体的表面积公式,熟练掌握它的表面积公式并灵活运用。
14.2560平方厘米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此求出长方体的表面积,再乘1.6即可解答。
【详解】×1.6
=(560+140+100)×2×1.6
=800×2×1.6
=2560(平方厘米)
答:至少要用2560平方厘米的包装纸。
【点睛】本题主要考查长方体表面积的应用,根据表面积公式即可解答。
15.162dm2
【分析】观察图可知,这个垃圾箱的表面积包括上面小正方体的表面积和下面大正方体的表面积之和,注意:上面的小正方体表面积只有4个侧面,下面的大正方体与上面小正方体连接部分是相通的,要挖去一个小正方形的面,据此列式解答。
【详解】5×5×6-2×2+2×2×4
=150-4+16
=162(dm2)
答:至少需要162dm2的铁皮。
【点睛】此题关键要理清需要计算哪几个面的面积,尤其注意下面的大正方体与上面小正方体连接部分是相通的,要挖去一个小正方形的面。
16.16平方米
【分析】1米=10分米,则5分米=0.5米,由于是通分管,通分管有4个面,缺少上,下两个面,根据长方体4个面的表面积公式:(长×高+宽×高)×2,把数代入公式即可求出一节通风管道的面积,再乘4即可求解。
【详解】5分米=0.5米
(0.5×2+0.5×2)×2
=(1+1)×2
=2×2
=4(平方米)
4×4=16(平方米)
答:做这些通风管道共用铁皮16平方米。
【点睛】本题主要考查长方体的表面积公式,熟练掌握它的公式并灵活运用。
17.60平方米
【分析】长方体有两个相对的面是正方形时,其它四个侧面形状相同面积相等,据此先计算做一个饼干盒需要贴纸的面积,最后乘1000即可。
【详解】10厘米=0.1米,15厘米=0.15米
0.1×0.15×4×1000
=0.015×4×1000
=0.06×1000
=60(平方米)
答:至少需要60平方米商标纸。
【点睛】本题主要考查长方体表面积公式的应用,分析题意求出一个饼干盒需要商标纸的面积是解答题目的关键。
18.123.2平方米
【分析】根据题意,做一个空调套的面积,就是求长方体5个面的面积和,根据长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,求出一个空调机套的表面积,再乘40个,即可解答。
【详解】50×40+(50×160+40×160)×2
=2000+(8000+6400)×2
=2000+14400×2
=2000+28800
=30800(平方厘米)
30800平方厘米=3.08平方米
3.08×40=123.2(平方米)
答:做40个这样的空调套至少要用123.2平方米的布。
【点睛】本题考查长方体表面积公式的应用,关键是熟记公式,注意单位名数的互换。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
必考专题:长方体(一)应用题-数学五年级下册北师大版
1.元宵节,奇思要制作一个底面是边长25cm的正方形,高是40cm的长方体灯笼,至少需要准备多少米的木条来搭这个灯笼框架?
2.做一个无盖的棱长为6分米的正方体铁盒,至少需要多大的面积的铁皮?(盖子的接口处可以忽略不计)
3.游泳中心新建了一个长50米、宽25米、深2米的游泳池。现要在游泳池四周和底面都贴上瓷砖,如果每平方米需要32元,一共需要多少元?
4.一个实验室长12米,宽9米,高4米。要粉刷实验室的天花板和四面墙壁,除去门窗和黑板的面积27.5平方米,平均每平方米用石灰0.2千克,一共需要石灰多少千克?
5.把一个长方体用三种不同的方法切成两个完全相同的长方体,结果它们的表面积分别增加了40、48、60平方厘米。原来的长方体的表面积是多少平方厘米?
6.有三个同样的长方体盒子,长10厘米,宽8厘米,高2厘米。现在要把这三个盒子包装在一起,最少需要多少平方厘米的包装纸?
7.将3盒这样的糖果包成一包(如下图),怎样包装最节省包装纸?至少需要多少平方厘米的包装纸?(接口处忽略不计)
8.一个长方体,如果高减少,就变成了一个棱长的正方体。那么长方体变成正方体后的表面积减少了多少?
9.把一块正方体木块锯成三个完全一样的长方体,表面积比原来增加了96平方分米。原正方体的表面积是多少平方分米?
10.有A、B、C三种规格的纸板各四张,从中选六张可做成一个长方体,这个长方体的表面积是多少?
11.一个底面是正方形的长方体铁桶,把它的侧面展开正好得到一个边长为40厘米的正方形。如果铁桶内装半桶水,与水接触的面的面积是多少?
12.大小不同的两个正方体积木粘在一起,构成下图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点。如果大积木的棱长为4分米,那么这个立体图形的表面积是多少平方分米?
13.黄老师给贫困山区的孩子买了4本同样的《十万个为什么》,每本书的长25厘米、宽18厘米、厚3厘米。包装这些书至少需要多大面积的包装纸?
14.一个长方体礼品盒,长28厘米,宽20厘米,高5厘米。如果包装这个礼品盒的用纸是其表面积的倍,至少要用多少平方厘米的包装纸?
15.游乐园里新增了一批垃圾箱,形状如图。它是由两个正方体组成的,其中小正方体的棱长是2dm,大正方体的棱长是5dm。小正方体无盖,便于人们扔垃圾。制作这样一个垃圾箱,至少需要多少平方分米的铁皮?
16.新世界中英文学校有四节长方体的通风管道,长宽各是5分米,高2米。做这些通风管道共用铁皮多少平方米?
17.饼干盒的长和宽都是10厘米,高是15厘米,要在盒子的四周贴上商标,印制1000张这样的商标,至少需要多少平方米商标纸?
18.加工厂要加工一批长方体立式空调机罩(没有底面),已知每台空调长50厘米,宽40厘米,高160厘米,做40个这样的空调机套至少要用多少平方米的布?
参考答案:
1.3.6米
【分析】根据“长方体的棱长和=(长+宽+高)×4”,即可求出至少需要准备多少米的木条来搭这个灯笼框架。
【详解】(25+25+40)×4
=90×4
=360(厘米)
360厘米=3.6米
答:至少需要准备3.6米的木条来搭这个灯笼框架。
【点睛】解答本题关键是熟练运用长方体的棱长和公式。注意单位的转化。
2.180平方分米
【分析】根据题意可知,求至少需要多大的面积的铁皮,就是求这个无盖正方体5个面的面积和,根据正方体表面积公式:表面积=棱长×棱长×5,代入数据,即可解答。
【详解】6×6×5
=36×5
=180(平方分米)
答:至少需要180平方分米大的面积的铁皮。
【点睛】本题考查正方体表面积公式的应用,关键是熟记公式。
3.49600元
【分析】根据题意,先求贴瓷砖的面积,即长方体游泳池5个面积的面积和;根据长方体表面积公式:表面积=长×宽+(长×高+宽×高)×2,代入数据,求出贴瓷砖的面积,再乘32,即可求出需要的钱数。
【详解】[50×25+(50×2+25×2)×2]×32
=[1250+(100+50)×2]×32
=[1250+150×2]×32
=[1250+300]×32
=1550×32
=49600(元)
答:一共需要49600元。
【点睛】熟练掌握长方体表面积公式是解答本题的关键。
4.49.7千克
【详解】[(12×4+9×4)×2+12×9-27.5]×0.2
=[(48+36)×2+108-27.5]×0.2
=(84×2+108-27.5)×0.2
=(168+108-27.5)×0.2
=(276-27.5)×0.2
=248.5×0.2
=49.7(千克)
答:一共需要石灰49.7千克。
5.148平方厘米
【分析】根据题意可知,把一个长方体切成两个完全相同的长方体,两个小长方体的表面积和比原来长方体的表面积增加两个切面的面积,用三种不同的方法切成两个完全相同的长方体,由此可分析出原长方体三个面的面积,把三种切法增加的面相加,就是原长方体的表面积。据此列式解答即可。
【详解】40+48+60
=88+60
=148(平方厘米)
答:原来的长方体的表面积是148平方厘米。
【点睛】此题的重点是要理解三种切法增加的面积和就是长方体的表面积。
6.376平方厘米
【分析】把三个长方体盒子叠在一起,有3种方式,重叠面积最大的叠法最省包装纸,即重叠底面时最省包装纸,据此解答。
【详解】因为三个面中底面最大,所以重合放在一起最省包装纸。
长方体的长是10厘米,宽是8厘米,高是2×3=6(厘米)
(10×8+10×6+8×6)×2
=(80+60+48)×2
=(140+48)×2
=188×2
=376(平方厘米)
答:最少需要376平方厘米的包装纸。
【点睛】最大面重合,得到的长方体的表面积最小,最小面重合,得到的长方体表面积最大。
7.将15厘米和10厘米这两个面相互叠加包装起来最节省包装纸;1200平方厘米
【分析】根据题意,将最大的面(15×10)互相叠加包装起来最省包装纸,根据长方体的表面积公式S=(ab+ah+bh)×2,代入数据解答即可。
【详解】由分析得:
将15厘米和10厘米这两个面相互叠加包装起来最节省包装纸。
(平方厘米)
答:至少需要1200平方厘米的包装纸。
【点睛】本题主要考查长方体表面积的实际应用与立体图形的拼接问题,关键是熟记公式,同时明确重合面越大越省包装纸。
8.240平方厘米
【分析】根据题意,一个长方体如果高减少6cm,就变成一个棱长10cm的正方体,长方体的长=长方体的宽=正方体棱长=10cm;求减少部分的面积,就是一个长是10cm,宽是10cm,高是6cm的长方体的侧面积;且这四个面相等;根据长方形面积公式:长×高,代入数据,即可解答。
【详解】10×6×4
=60×4
=240(cm2)
答:长方体变成正方体后的表面积减少了240平方厘米。
【点睛】解答本题的关键是明确减少后的长方体的长与宽和正方体棱长的关系。
9.144平方分米
【分析】正方体锯成三个完全一样的长方体,表面积多了四个正方形的面积。用除法求出一个正方形的面积,再根据“正方体表面积=正方形面积×6”计算即可。
【详解】96÷4×6
=24×6
=144(平方分米)
答:原来正方体的表面积是144平方分米。
【点睛】本题考查的是正方形表面积的计算,明确正方体锯成长方体,表面积增加的面积是几个正方形的面积,是解答本题的关键。
10.选四张A、两张C可做成一个长方体。190平方分米
【分析】根据长方体的特征,相对的面完全相同,把12条棱平均分成3组,分别是长、宽、高,由此可知,需要选四张A、两张C组成一个长方体,长方体的表面积就是6个面的面积之和,据此解答。
【详解】选四张A、两张C可做成一个长方体。
5×5×2+5×7×4
=50+140
=190(平方分米)
答:长方体的表面积是190平方分米。
【点睛】此题考查了长方体的特征以及表面积计算,根据长方体特征,先选择出所需要的纸板是解题关键。
11.900平方厘米
【分析】这是一个无盖桶,与水接触面的面积即桶的底面和四个侧面面积,根据桶的侧面展开图是边长为40厘米的正方形,求出有水部分的长和宽。根据长方体的面积公式求出一个面的面积再乘4即可得到四个侧面的面积,再加桶的底面积即可得到答案。
【详解】40÷4=10(厘米)
底面面积:10×10=100(平方厘米)
侧面面积:10×20×4=800(平方厘米)
与水接触的面积:10×10+10×20×4=900(平方厘米)
答:与水接触的面的面积是900平方厘米。
【点睛】关键是弄清楚与水接触的面是什么,再根据侧面展开图为边长是40厘米的正方形这个线索进行求解。
12.128平方分米
【分析】如图,因为小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点,所以大正方体一个面的面积是小正方体一个面的面积的2倍,因此,这个立方体图形的表面积=大正方体的表面积+小正方体四个侧面的面积;据此解答。
【详解】由分析得:
6×4×4+4×(4×4÷2)
=96+4×8
=96+32
=128(平方分米)
答:那么这个立体图形的表面积是128平方分米。
【点睛】本题主要考查组合体的表面积计算,关键是明确大正方体一个面的面积是小正方体一个面的面积的2倍。
13.1932平方厘米
【分析】当把4本书一本一本封面向上放在一起最节省包装纸,即此时的长是25厘米,宽是18厘米,高是:3×4=12(厘米),根据长方体的表面积公式:(长×宽+长×高+宽×高)×2,把数代入公式即可求解。
【详解】由分析可知:把4本书叠放在一起最节省包装纸。
此时的高:4×3=12(厘米)
(25×18+25×12+18×12)×2
=(450+300+216)×2
=966×2
=1932(平方厘米)
答:包装这些书至少需要1932平方厘米的包装纸。
【点睛】本题主要考查长方体的表面积公式,熟练掌握它的表面积公式并灵活运用。
14.2560平方厘米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此求出长方体的表面积,再乘1.6即可解答。
【详解】×1.6
=(560+140+100)×2×1.6
=800×2×1.6
=2560(平方厘米)
答:至少要用2560平方厘米的包装纸。
【点睛】本题主要考查长方体表面积的应用,根据表面积公式即可解答。
15.162dm2
【分析】观察图可知,这个垃圾箱的表面积包括上面小正方体的表面积和下面大正方体的表面积之和,注意:上面的小正方体表面积只有4个侧面,下面的大正方体与上面小正方体连接部分是相通的,要挖去一个小正方形的面,据此列式解答。
【详解】5×5×6-2×2+2×2×4
=150-4+16
=162(dm2)
答:至少需要162dm2的铁皮。
【点睛】此题关键要理清需要计算哪几个面的面积,尤其注意下面的大正方体与上面小正方体连接部分是相通的,要挖去一个小正方形的面。
16.16平方米
【分析】1米=10分米,则5分米=0.5米,由于是通分管,通分管有4个面,缺少上,下两个面,根据长方体4个面的表面积公式:(长×高+宽×高)×2,把数代入公式即可求出一节通风管道的面积,再乘4即可求解。
【详解】5分米=0.5米
(0.5×2+0.5×2)×2
=(1+1)×2
=2×2
=4(平方米)
4×4=16(平方米)
答:做这些通风管道共用铁皮16平方米。
【点睛】本题主要考查长方体的表面积公式,熟练掌握它的公式并灵活运用。
17.60平方米
【分析】长方体有两个相对的面是正方形时,其它四个侧面形状相同面积相等,据此先计算做一个饼干盒需要贴纸的面积,最后乘1000即可。
【详解】10厘米=0.1米,15厘米=0.15米
0.1×0.15×4×1000
=0.015×4×1000
=0.06×1000
=60(平方米)
答:至少需要60平方米商标纸。
【点睛】本题主要考查长方体表面积公式的应用,分析题意求出一个饼干盒需要商标纸的面积是解答题目的关键。
18.123.2平方米
【分析】根据题意,做一个空调套的面积,就是求长方体5个面的面积和,根据长方体表面积公式:长×宽+(长×高+宽×高)×2,代入数据,求出一个空调机套的表面积,再乘40个,即可解答。
【详解】50×40+(50×160+40×160)×2
=2000+(8000+6400)×2
=2000+14400×2
=2000+28800
=30800(平方厘米)
30800平方厘米=3.08平方米
3.08×40=123.2(平方米)
答:做40个这样的空调套至少要用123.2平方米的布。
【点睛】本题考查长方体表面积公式的应用,关键是熟记公式,注意单位名数的互换。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
